22.5 综合与实践 测量与误差 课件 (共25张PPT)
文档属性
| 名称 | 22.5 综合与实践 测量与误差 课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 19:37:59 | ||
图片预览




文档简介
(共25张PPT)
沪科版 九年级上册
22.5 综合与实践
测量与误差
活动目的:
知识与技能:
掌握和综合运用三角形相似的判定条件和性质.
过程与方法:
通过测量旗杆的高度,家运用所学知识解决问题.
情感态度与价值观:
通过问题情境的设置,培养积极的进取精神,增强数学
学习的自信心. 实现生生之间的交流合作,体现数学
知识解决实际问题的价值.
活动重点:
综合运用相似三角形判定,性质解决实际问题.
活动难点:
解决在操作过程中如何与课本中有关知识相联系.
关键:
抓住测量方法,结合所学,进行问题的解决.
教学准备:
教师:必要的测量工具,设计活动方法.
学生:标杆,镜子,皮尺等测量工具.
实践应用
利用相似三角形的有关知识测量旗杆的高度.
方式:
全班同学分成六人小组,选出组长,
分头测量学校操场旗杆的高度.
先集中讨论方案,再分散实际操作,
最后集中总结交流.
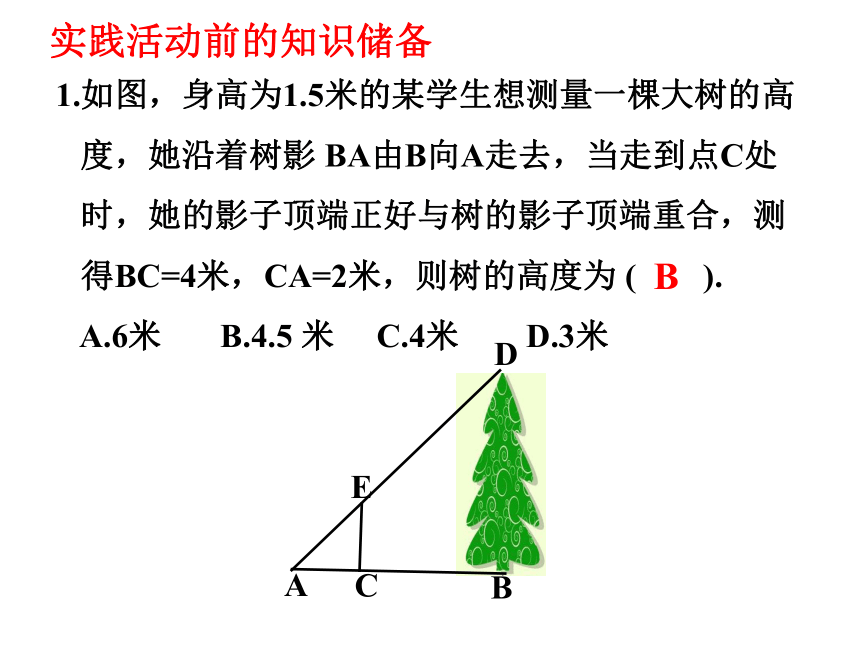
1.如图,身高为1.5米的某学生想测量一棵大树的高
度,她沿着树影 BA由B向A走去,当走到点C处
时,她的影子顶端正好与树的影子顶端重合,测
得BC=4米,CA=2米,则树的高度为 ( ).
A.6米 B.4.5 米 C.4米 D.3米
A
B
D
C
E
B
实践活动前的知识储备
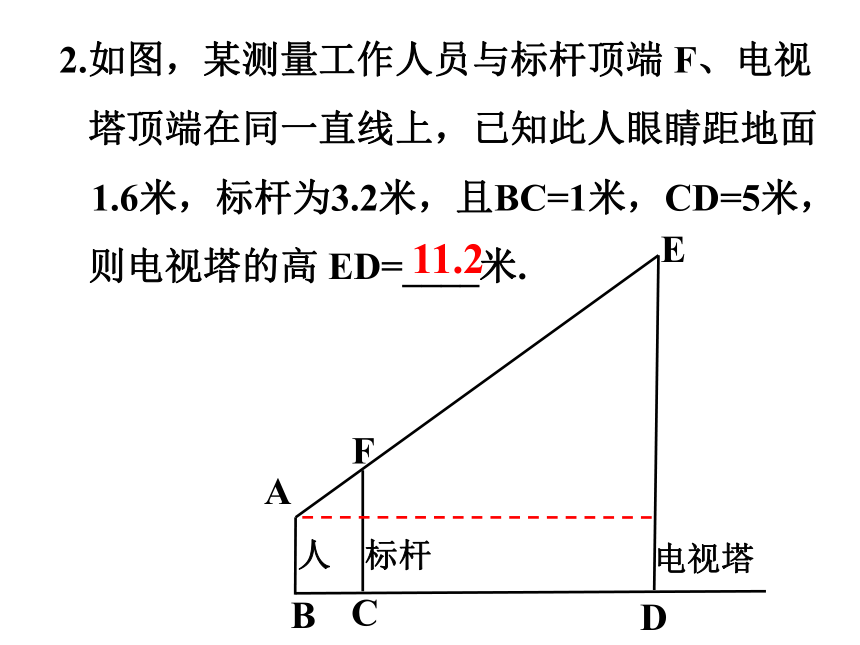
2.如图,某测量工作人员与标杆顶端 F、电视
塔顶端在同一直线上,已知此人眼睛距地面
1.6米,标杆为3.2米,且BC=1米,CD=5米,
则电视塔的高 ED=____米.
A
B
C
D
E
F
人
标杆
电视塔
11.2
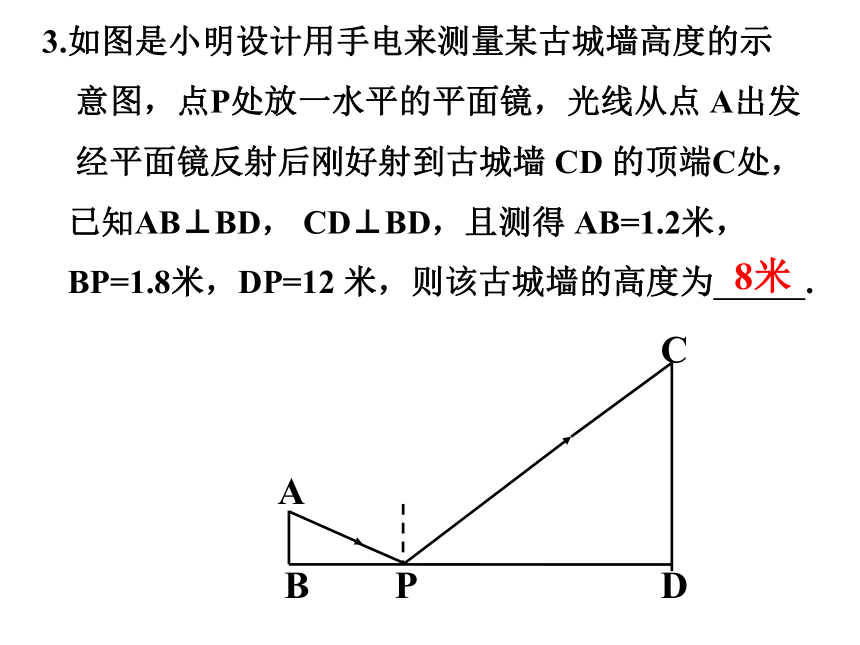
3.如图是小明设计用手电来测量某古城墙高度的示
意图,点P处放一水平的平面镜,光线从点 A出发
经平面镜反射后刚好射到古城墙 CD 的顶端C处,
已知AB⊥BD, CD⊥BD,且测得 AB=1.2米,
BP=1.8米,DP=12 米,则该古城墙的高度为 .
A
B
C
D
P
8米
利用相似三角形解决实际问题的一般步骤:
(1)根据题意画出示意图;
(2)将题目中的已知量或已知关系转化为示意
图中的已知线段,已知角或它们之间的关系;
(3)利用相似三角形的对应边成比例的性质,
建立线段之间的比例式,求出未知量;
(4)写出答案.
测量工具
皮尺、标杆、平面镜、三角板及测角器等.
实践活动前的感知准备
测量旗杆高度的方法有:
(1)利用阳光下的影子测量旗杆的高度;
(2)利用标杆测量旗杆的高度;
(3)利用镜子的反射测量旗杆的高度;
(4)利用特殊角测量旗杆的高度.
实践活动
测量旗杆高度的方法一:利用阳光下的影子测量
1.画出示意图;
AB、BC分别是旗杆的高度与影长
DE、 EF分别是观测者的高度与影长.
2.测量方法
测量者直立于旗杆影子的顶端C处
3.测量数据
4.计算方法
测量旗杆影长BC= a ,
观测者的身高DE=b ,
观测者的影长EF= c .
由△ABC∽△DEF,得
AB:DE=BC:EF
∴AB=
BC·DE
EF
(E)
A
B
D
F
C
=
ab
c
测量旗杆高度的方法二:利用标杆测量
1.画出示意图;
2.测量方法
3.测量数据
4.计算方法
AB、CD、EF分别是旗杆、标杆,观测者的眼睛距地面的高度,
BD、 BF分别是标杆底端、观测者底端到旗杆的距离.
设旗杆的高度为h,
标杆的高度CD= b,
观测者眼睛距地面的高度EF=a,
标杆底端到旗杆的距离BD= c,
观测者底端到旗杆的距离BF= d.
∴h=
d·(b-a)
d-c
设点E为观测者的眼睛,在观测者EF与旗杆AB之间的地面上直立一根高度适当的标杆CD ,点A、C、E在同一直线上.
A
B
C
D
E
F
测量旗杆高度的方法三:利用镜子的反射测量
1.画出示意图;
2.测量方法
3.测量数据
4.计算方法
点O表示镜子,AB表示旗杆的高度,CD观测者眼睛距地面的
高度,OB、 OD分别表示旗杆底端、观测者底端到镜子的距离.
设旗杆的高度为h,
观测者眼睛距地面的高度CD= a,
旗杆底端到镜子的距离OB= b,
观测者底端到镜子的距离OD= c .
∴h=
ab
c
在观测者CD与旗杆AB之间的地面上平放一面镜子,调整观测者的位置,使旗杆顶端在镜子中的像与镜子上的标记重合,并使点B、O、D在同一直线上.
A
B
C
D
O
测量旗杆高度的方法四:利用特殊角测量
1.画出示意图;
2.测量方法
3.测量数据
4.计算方法
AB表示旗杆的高度,EF表示观测者的眼睛距地面的高度.
设旗杆的高度为h,
观测者眼睛距地面的高度BF= d ,
观测者底端到旗杆的距离EF= a .
通过测角器观察旗杆顶端A,使测角器的显示的读数为60°(可以是45°,30°),利用AB=AM + BM= ME+EF.
3
∴h= d+a.
3
A
B
M
C
E
F
问题①请你用这四种方法进行旗杆测量,并将测量数据记录于下列表格中.
测量旗杆的高度
测量次序
1
2
3
测量次
计算结果
方法一
方法二
方法三
方法四
问题②你觉得何种方法操作简便,又是何种方法测得的数据更准确 你还有其他的测量方法吗
问题③ 在测量中,每次的测量数据都有差异,你是如何处理的,你测量了几次
问题④ 几种测量方法为何有误差,如何改进 请对测量误差进行思考,查找误差原因.
活动评价(评价自己与他人):
1.本节课你有哪些收获(知识方面和操作方面)?
在运用科学知识进行实践过程中,你具有了
哪些能力 你是否想到最优的方法?
把自己在与同伴合作交流中, 最满意的表现说
给大家听听.
2.你的同伴中你认为最值得你学习的是哪几个人?
1.相同时刻的物高与影长成比例,若一座房
子在地面上的影长是 30 m,同时一位身高
为 160 cm的人的影长是2.4m,则这座房子
的高是( ).
A.20 m B.2000 m C.45 m D.4500 m
学以致用
B
2.要测量出一棵树的高度,除了测量出人
高与人的影长外,还需要测出 ( ).
A.仰角 B. 树的影长
C. 标杆的影长 D. 都不需要
B
3.如图所示,为测量学校旗杆的高度,小东用长
3.2m的竹竿作测量工具,移动竹竿,使竹竿顶端
与旗杆顶端的子给好落在地面的同一点,此时,
竹竿与这一点相距8m.与旗杆相距22m,则旗杆
的高为( ).
A.8.8 m B.10 m
C.12 m D.14m
C
8m
22m
学以致用
4.如图,九年级1班课外活动小组利用标杆测量学校
旗杆的高度.已知标杆高度CD=3 m,标杆与旗杆的
水平距离 BD=15 m,人的眼睛与地面的高度 EF
=1.6 m,人与标杆 CD 的水平距离 DF=2 m,人的
眼睛E、标杆顶点 C和旗杆顶点A在同一直线上.
则旗杆 AB 的高度为 .
A
B
C
D
E
F
D
B
A
C
E
5.如图所示,在距离树高AB 18米的地面上平放着一
面镜子E,人退后到距镜子2.1米的D处,在镜子里
恰看见树顶.若人眼距地面1.4米,则树高为 m.
12
6.如图,某同学拿着一把有刻度的尺子,站在距电线
杆 30m的位置,把手臂向前伸直,将尺子竖直,看
到尺子遮住电线杆时尺子的刻度为12 cm,已知臂
长 60 cm,则电线杆的高度为( ).
A.2.4m B.24m C.0.6 m D.6 m
手臂
尺子
电线杆
D
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
22.5 综合与实践
测量与误差
活动目的:
知识与技能:
掌握和综合运用三角形相似的判定条件和性质.
过程与方法:
通过测量旗杆的高度,家运用所学知识解决问题.
情感态度与价值观:
通过问题情境的设置,培养积极的进取精神,增强数学
学习的自信心. 实现生生之间的交流合作,体现数学
知识解决实际问题的价值.
活动重点:
综合运用相似三角形判定,性质解决实际问题.
活动难点:
解决在操作过程中如何与课本中有关知识相联系.
关键:
抓住测量方法,结合所学,进行问题的解决.
教学准备:
教师:必要的测量工具,设计活动方法.
学生:标杆,镜子,皮尺等测量工具.
实践应用
利用相似三角形的有关知识测量旗杆的高度.
方式:
全班同学分成六人小组,选出组长,
分头测量学校操场旗杆的高度.
先集中讨论方案,再分散实际操作,
最后集中总结交流.
1.如图,身高为1.5米的某学生想测量一棵大树的高
度,她沿着树影 BA由B向A走去,当走到点C处
时,她的影子顶端正好与树的影子顶端重合,测
得BC=4米,CA=2米,则树的高度为 ( ).
A.6米 B.4.5 米 C.4米 D.3米
A
B
D
C
E
B
实践活动前的知识储备
2.如图,某测量工作人员与标杆顶端 F、电视
塔顶端在同一直线上,已知此人眼睛距地面
1.6米,标杆为3.2米,且BC=1米,CD=5米,
则电视塔的高 ED=____米.
A
B
C
D
E
F
人
标杆
电视塔
11.2
3.如图是小明设计用手电来测量某古城墙高度的示
意图,点P处放一水平的平面镜,光线从点 A出发
经平面镜反射后刚好射到古城墙 CD 的顶端C处,
已知AB⊥BD, CD⊥BD,且测得 AB=1.2米,
BP=1.8米,DP=12 米,则该古城墙的高度为 .
A
B
C
D
P
8米
利用相似三角形解决实际问题的一般步骤:
(1)根据题意画出示意图;
(2)将题目中的已知量或已知关系转化为示意
图中的已知线段,已知角或它们之间的关系;
(3)利用相似三角形的对应边成比例的性质,
建立线段之间的比例式,求出未知量;
(4)写出答案.
测量工具
皮尺、标杆、平面镜、三角板及测角器等.
实践活动前的感知准备
测量旗杆高度的方法有:
(1)利用阳光下的影子测量旗杆的高度;
(2)利用标杆测量旗杆的高度;
(3)利用镜子的反射测量旗杆的高度;
(4)利用特殊角测量旗杆的高度.
实践活动
测量旗杆高度的方法一:利用阳光下的影子测量
1.画出示意图;
AB、BC分别是旗杆的高度与影长
DE、 EF分别是观测者的高度与影长.
2.测量方法
测量者直立于旗杆影子的顶端C处
3.测量数据
4.计算方法
测量旗杆影长BC= a ,
观测者的身高DE=b ,
观测者的影长EF= c .
由△ABC∽△DEF,得
AB:DE=BC:EF
∴AB=
BC·DE
EF
(E)
A
B
D
F
C
=
ab
c
测量旗杆高度的方法二:利用标杆测量
1.画出示意图;
2.测量方法
3.测量数据
4.计算方法
AB、CD、EF分别是旗杆、标杆,观测者的眼睛距地面的高度,
BD、 BF分别是标杆底端、观测者底端到旗杆的距离.
设旗杆的高度为h,
标杆的高度CD= b,
观测者眼睛距地面的高度EF=a,
标杆底端到旗杆的距离BD= c,
观测者底端到旗杆的距离BF= d.
∴h=
d·(b-a)
d-c
设点E为观测者的眼睛,在观测者EF与旗杆AB之间的地面上直立一根高度适当的标杆CD ,点A、C、E在同一直线上.
A
B
C
D
E
F
测量旗杆高度的方法三:利用镜子的反射测量
1.画出示意图;
2.测量方法
3.测量数据
4.计算方法
点O表示镜子,AB表示旗杆的高度,CD观测者眼睛距地面的
高度,OB、 OD分别表示旗杆底端、观测者底端到镜子的距离.
设旗杆的高度为h,
观测者眼睛距地面的高度CD= a,
旗杆底端到镜子的距离OB= b,
观测者底端到镜子的距离OD= c .
∴h=
ab
c
在观测者CD与旗杆AB之间的地面上平放一面镜子,调整观测者的位置,使旗杆顶端在镜子中的像与镜子上的标记重合,并使点B、O、D在同一直线上.
A
B
C
D
O
测量旗杆高度的方法四:利用特殊角测量
1.画出示意图;
2.测量方法
3.测量数据
4.计算方法
AB表示旗杆的高度,EF表示观测者的眼睛距地面的高度.
设旗杆的高度为h,
观测者眼睛距地面的高度BF= d ,
观测者底端到旗杆的距离EF= a .
通过测角器观察旗杆顶端A,使测角器的显示的读数为60°(可以是45°,30°),利用AB=AM + BM= ME+EF.
3
∴h= d+a.
3
A
B
M
C
E
F
问题①请你用这四种方法进行旗杆测量,并将测量数据记录于下列表格中.
测量旗杆的高度
测量次序
1
2
3
测量次
计算结果
方法一
方法二
方法三
方法四
问题②你觉得何种方法操作简便,又是何种方法测得的数据更准确 你还有其他的测量方法吗
问题③ 在测量中,每次的测量数据都有差异,你是如何处理的,你测量了几次
问题④ 几种测量方法为何有误差,如何改进 请对测量误差进行思考,查找误差原因.
活动评价(评价自己与他人):
1.本节课你有哪些收获(知识方面和操作方面)?
在运用科学知识进行实践过程中,你具有了
哪些能力 你是否想到最优的方法?
把自己在与同伴合作交流中, 最满意的表现说
给大家听听.
2.你的同伴中你认为最值得你学习的是哪几个人?
1.相同时刻的物高与影长成比例,若一座房
子在地面上的影长是 30 m,同时一位身高
为 160 cm的人的影长是2.4m,则这座房子
的高是( ).
A.20 m B.2000 m C.45 m D.4500 m
学以致用
B
2.要测量出一棵树的高度,除了测量出人
高与人的影长外,还需要测出 ( ).
A.仰角 B. 树的影长
C. 标杆的影长 D. 都不需要
B
3.如图所示,为测量学校旗杆的高度,小东用长
3.2m的竹竿作测量工具,移动竹竿,使竹竿顶端
与旗杆顶端的子给好落在地面的同一点,此时,
竹竿与这一点相距8m.与旗杆相距22m,则旗杆
的高为( ).
A.8.8 m B.10 m
C.12 m D.14m
C
8m
22m
学以致用
4.如图,九年级1班课外活动小组利用标杆测量学校
旗杆的高度.已知标杆高度CD=3 m,标杆与旗杆的
水平距离 BD=15 m,人的眼睛与地面的高度 EF
=1.6 m,人与标杆 CD 的水平距离 DF=2 m,人的
眼睛E、标杆顶点 C和旗杆顶点A在同一直线上.
则旗杆 AB 的高度为 .
A
B
C
D
E
F
D
B
A
C
E
5.如图所示,在距离树高AB 18米的地面上平放着一
面镜子E,人退后到距镜子2.1米的D处,在镜子里
恰看见树顶.若人眼距地面1.4米,则树高为 m.
12
6.如图,某同学拿着一把有刻度的尺子,站在距电线
杆 30m的位置,把手臂向前伸直,将尺子竖直,看
到尺子遮住电线杆时尺子的刻度为12 cm,已知臂
长 60 cm,则电线杆的高度为( ).
A.2.4m B.24m C.0.6 m D.6 m
手臂
尺子
电线杆
D
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
