3.1.2等式的性质

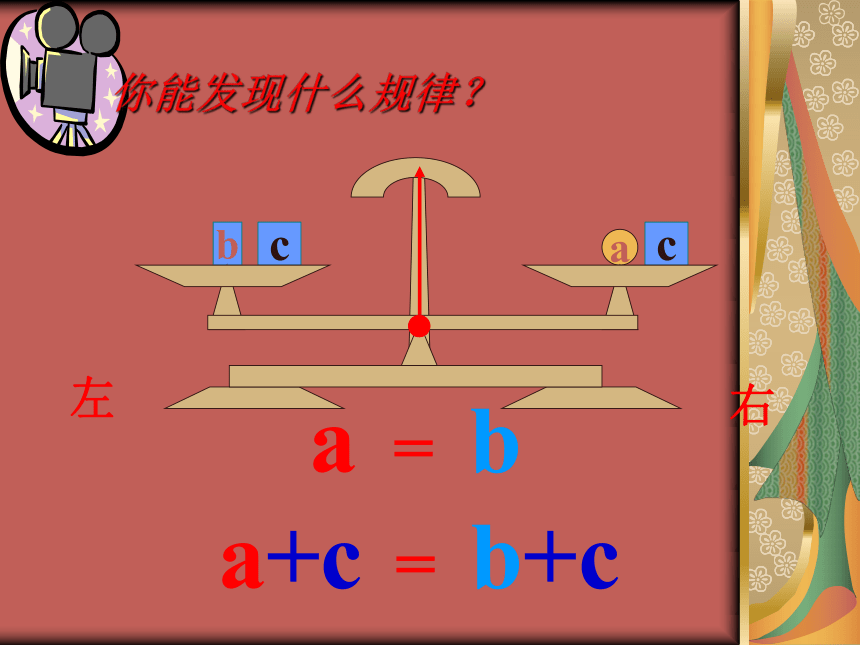
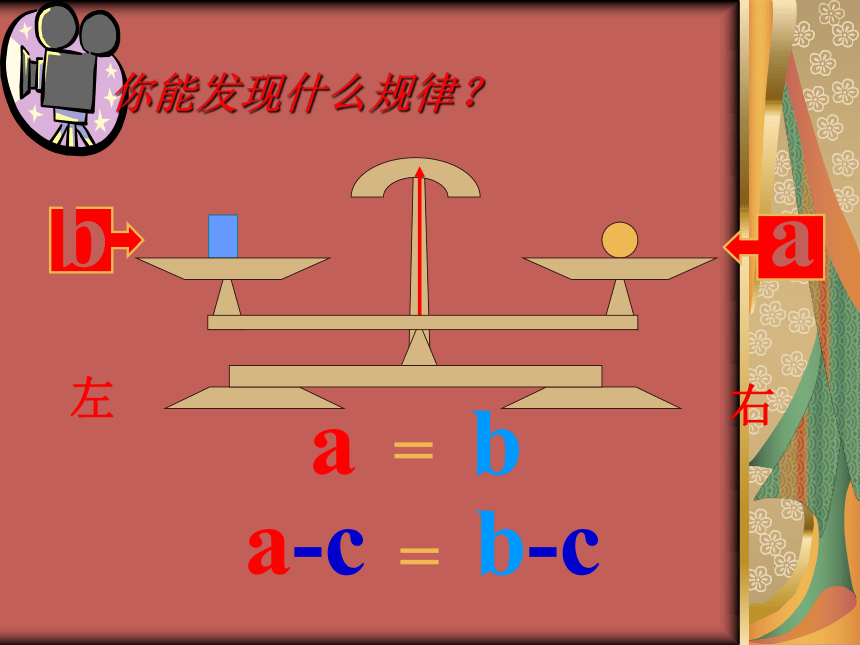
课件32张PPT。等式性质3.2 像这样用等号“=”表示相等关系的式子叫等式a自主探索：你能发现什么规律？右左a你能发现什么规律？右左ab你能发现什么规律？右左ba你能发现什么规律？a = b右左ba你能发现什么规律？a = bc右左acb你能发现什么规律？a = b右左cbca你能发现什么规律？a = ba+c b+c=右左cc你能发现什么规律？a = b右左c你能发现什么规律？a = b右左你能发现什么规律？a = ba-c b-c=右左1. 如果 七年级(1)班的学生人数=七年级(2)班的学生人数，
现在每班增加2名学生，那么七年级(1)班与七班级(2)班的
学生人数还相等吗？相 等 如果每班减少3名学生，那么这两个班的学生人数还相等吗？相 等归纳等式的性质1:
等式两边同加（或同减）同一个数（或式子），结果仍相等。
如果a=b，那么a+c=b+cba你能发现什么规律？a = b右左ba你能发现什么规律？a = b右左ab2a = 2bba你能发现什么规律？a = b右左bbaa3a = 3bba你能发现什么规律？a = b右左bbbbbbaaaaaaC个 C个ac = bcba你能发现什么规律？a = b右左等式的性质2:
等式两边都乘以同一个数，或都除以同一个
不为0的数，结果仍相等。
如果a=b，那么ac=bc；如果a=b（c ≠ 0），那么归纳举
例（3）如果 ，那么3a= .例1 填空，并说明理由.解 因为a+2=b+7 ，由等式性质1可知，
等式两边都减去2，得a + 2 - 2 = b + 7 -2，即 a = b + 5 .解 因为3x=9y，由等式性质2可知，等式两边都除以3，得 即 x = 3y.（1）如果a+2 = b+7,那么a= ；（2）如果3x = 9x，那么 x= ；解 因为 ，由等式性质2可知，等式两边都乘6，得

即 3a = 2b .×6×6=3a = 2bx = 3ya = b + 5举
例例2 判断下列等式变形是否正确，并说明理由.（1）如果a -3=2b -5,那么a=2b -8；（2）如果 ，那么 10x -5=16x -8.解 错误. 由等式性质1可知，等式两边都加上3，
得 a-3+3=2b-5+3
即 a = 2b - 2 .解 正确由等式性质2可知，等式两边都乘20，得×20=×20即 5(2x-1) = 4(4x-2)去括号，得 10x-5=16x-8.例3 利用等式性质解下列方程：（1）x+7=26 (2)-4=x-6解（1）两边减7,
得 x+7-7=26-7
于是 x=19(2)两边同时加上6，
得 -4+6=x-6+6
于是 x=2举
例例4、利用等式性质解下列方程 （1）-5x=20 (2) = -1举
例学以致用：1.口答下面各题(1)从x=y能否得到x+5=y+5？为什么？
(2)从x=y能否得到 = 为什么？
(3)从a+2=b+2能否得到a=b？为什么？
(4)从-3a=-3b能否得到a=b？为什么？ 2. 请在括号中写出下列等式变形的理由：（1）如果 a-3=b+4，那么a=b+7 ( )；（2）如果 3x=2y，那么 ( )；等式性质1等式性质2（3）如果 ，那么x=2y ( )；等式性质2（4）如果2a+3=3b-1，那么2a-6=3b-10 ( ).等式性质1 3. 判断下列等式变形是否正确，并说明理由.（1）若 ，则a+3=3b-3；不正确，应该是 a+9=3b-3.（2）若 2x-6=4y-2，则 x-3=2y-2.不正确，应该是 x-3=2y-1.（1）x-5=6 (2) x+4=9 (3) y+7=-1 4、利用等式性质解下列方程：(巩固等式的性质1)解:(1)两边同加上5,
得 X-5+5=6+5
于是 X=11
解:(2)两边同减去4,
得 X+4-4=9-4
于是 X=5解:(3)两边同减去7,
得 X+7-7=-1-7
于是 X=-85、利用等式性质解下列方程：（巩固等式的性质2）（1）3y=-2 (2)-0.3x=12 (3)- y =12解(1)两边除以3
得 =
于是 y=
解(2)两边除以-0.3
得 =
于是 x=-40
解(2)两边除以-1
得 =
于是 y=-12
算一算，试一试 你能否求出下列方程的解。
(1) 4x=24
(2) x +1= 3
(3) 46x=230
(4) 2500+900x = 15000本节课你学到了什么？课堂小结:（1）等式的性质。（2）等式性质的应用。等式性质1：等式两边加（或减）同一个数（或式子），结果仍相等。 等式性质2：等式的两边乘同一个数，或除以同一个不为0的数，所的结果仍相等。利用等式的性质解方程，就是把方程变形， 变为 x = a（a为常数）的形式。习 题 3.11）P83页第4题作 业