2013-2014学年度黑龙江省大庆房顶中学第一学期初二数学期末测试卷(附答案)
文档属性
| 名称 | 2013-2014学年度黑龙江省大庆房顶中学第一学期初二数学期末测试卷(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 174.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-30 14:47:57 | ||
图片预览



文档简介
2013~2014年度大庆市房顶中学初二数学期末测试卷
一.选择题
1.下列计算正确的是( )
A. a3+a2=2a5 B. (﹣2a3)2=4a6 C. (a+b)2=a2+b2 D. a6÷a2=a3
2.若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是( )
A. x+y+z=0 B. x+y﹣2z=0 C. y+z﹣2x=0 D. z+x﹣2y=0
3.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是
A. 40° B. 60° C. 80° D. 120°
3题 6题 8题 9题 11题
4.恩施生态旅游初步形成,2011年全年实现旅游综合收入9 086 600 000元.数9 086 600 000用科学记数法表示(保留三个有效数字),正确的是( )
A. 9.09×109 B. 9.087×1010 C. 9.08×109 D. 9.09×108
5.如图,有四张不透明的卡片除正面的算式不同外,其余完全相同,将它们背面朝上洗匀后,从中随机抽取一张,则抽到得卡片上算式正确的概率是( )
A. B. C. D. 1
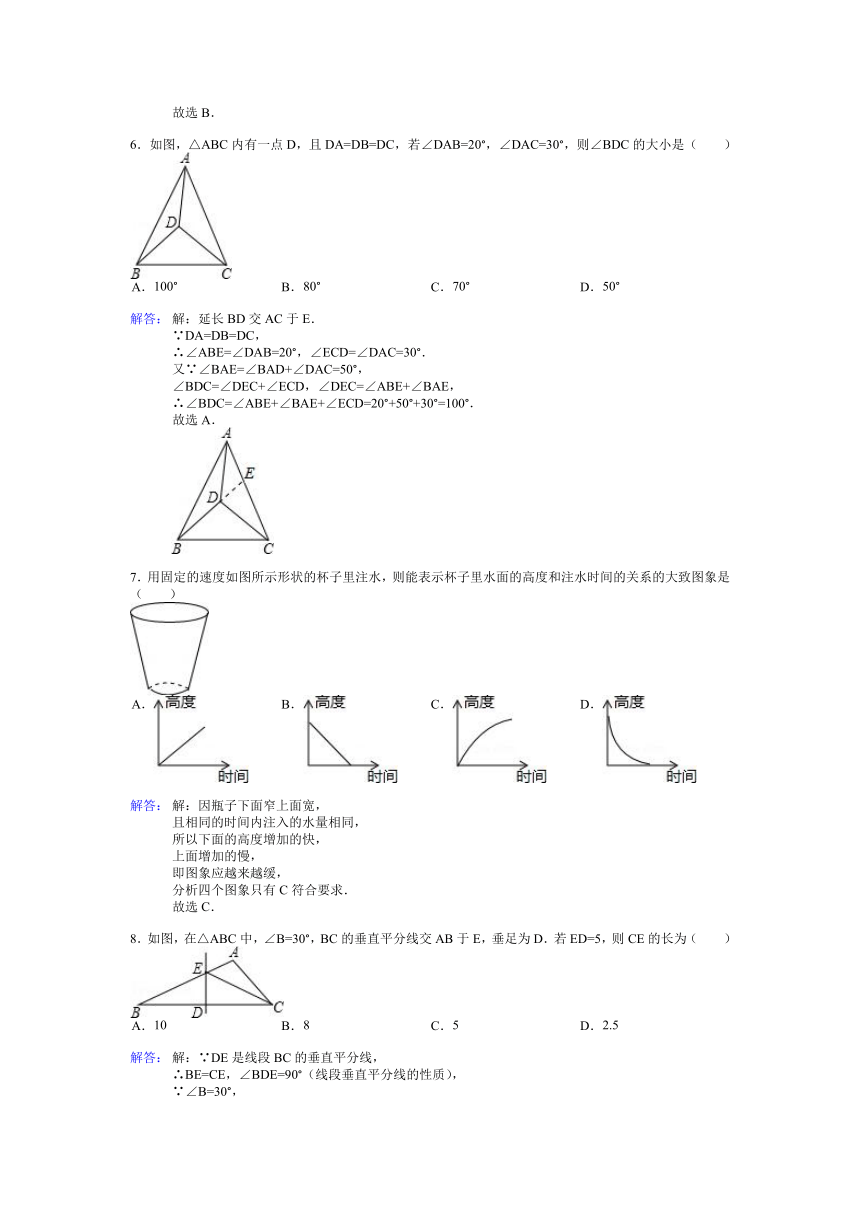
6.如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是
A. 100° B. 80° C. 70° D. 50°
7.用固定的速度如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( )
A. B. C. D.
8.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( )
A. 10 B. 8 C. 5 D. 2.5
9.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A. PO B. PQ C. MO D. MQ
10.利用基本尺规作图,下列条件中,不能作出唯一直角三角形的是( )
A. 已知斜边和一锐角 B. 已知一直角边和一锐角
C. 已知斜边和一直角边 D. 已知两个锐角
11.已知:如图,点D、E分别在AB、AC边上,△ABE≌△ACD,AC=15,BD=9,则线段AD的长是( )
A. 6 B. 9 C. 12 D. 15
2.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A. 21 B. 28 C. 36 D. 45
二.填空题(共6小题)
13.设a>b>0,a2+b2﹣6ab=0,则()2的值等于 _________ .
14.如图,CD⊥AB,垂足为C,∠1=130°,则∠2= _________ 度.
15.2011年湛江市社会经济实现快速发展,全市城镇居民全年可支配收入约为17000元,数据17000用科学记数法表示为 _________ .(保留两位有效数字)
16.掷一枚质地均匀的骰子,骰子的六个面上分别标有数字1~6,掷得朝上的一面的数字为奇数的概率是 _________ .
17.在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是_________.
18.五一节某超市搞促销活动:①一次性购物不超过150元不享受优惠;②一次性购物超过150元但不超过500元一律九折;③一次性购物超过500元一律八折.王宁两次购物分别付款120元、432元,若王宁一次性购买与上两次相同的商品,则应付款 _________ 元.
三.解答题(共8小题)
19.计算:
20.某位同学做一道题:已知两个多项式A、B,求A﹣B的值.他误将A﹣B看成A+B,求得结果为3x2﹣3x+5,已知B=x2﹣x﹣1.(1)求多项式A;(2)求A﹣B的正确答案.
21.先化简,再求值:2x2+(﹣x2+3xy+2y2)﹣( x2﹣xy+2y2),其中 x=,y=3.
22.如图,直线AB与CD相交于O,OE平分∠AOB,OF平分∠COD.
(1)图中与∠COA互补的角是 _________ ;(把符合条件的所有角都写出来)
(2)如果∠AOC=35°,求∠EOF的度数.
24.小亮家距离学校8千米,昨天早晨,小亮骑车上学途中,自行车“爆胎”,恰好路边有“自行车”维修部,几分钟后车修好了,为了不迟到,他加快了骑车到校的速度.回校后,小亮根据这段经历画出如下图象.该图象描绘了小亮行的路程S与他所用的时间t之间的关系.请根据图象,解答下列问题:
(1)小亮行了多少千米时,自行车“爆胎”?修车用了几分钟?
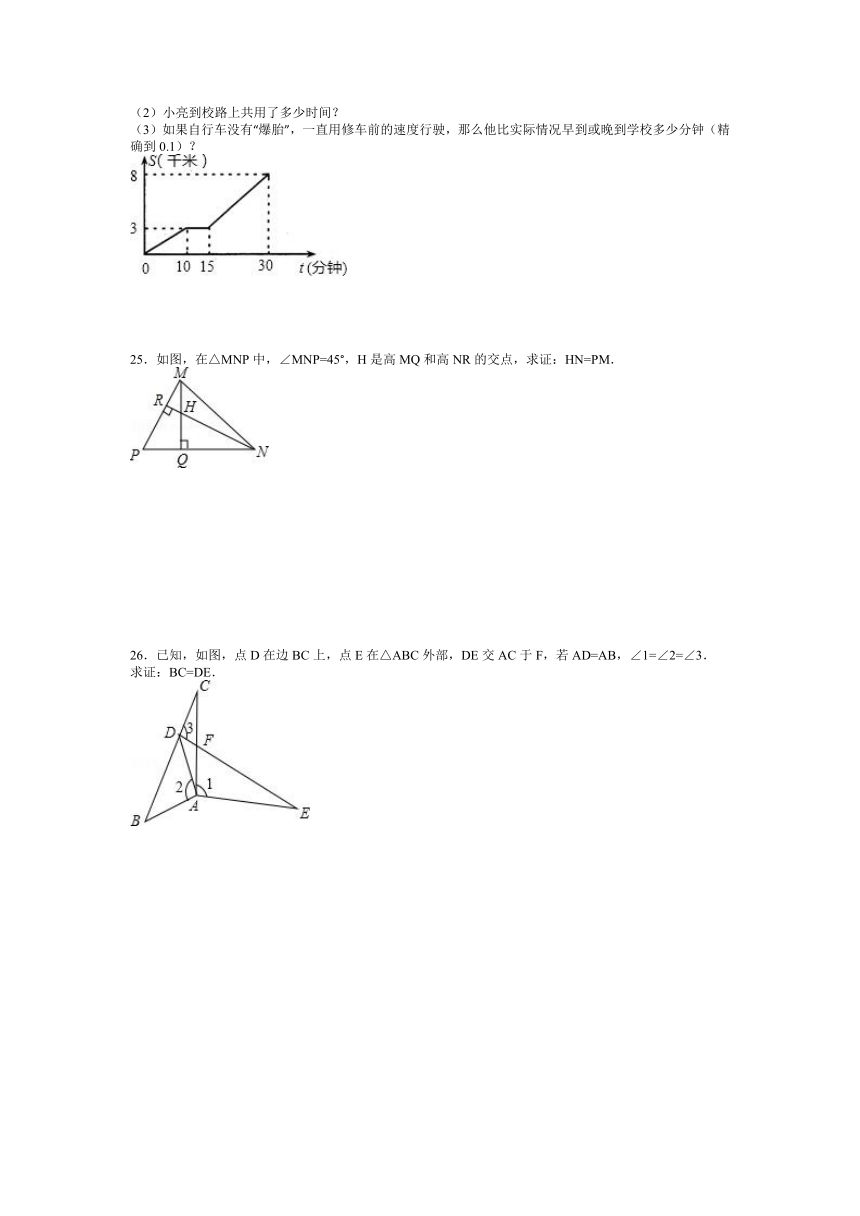
(2)小亮到校路上共用了多少时间?
(3)如果自行车没有“爆胎”,一直用修车前的速度行驶,那么他比实际情况早到或晚到学校多少分钟(精确到0.1)?
25.如图,在△MNP中,∠MNP=45°,H是高MQ和高NR的交点,求证:HN=PM.
26.已知,如图,点D在边BC上,点E在△ABC外部,DE交AC于F,若AD=AB,∠1=∠2=∠3.
求证:BC=DE.
2013~2014年度大庆市房顶中学初二期末测试卷
参考答案与试题解析
一.选择题(共12小题)
1.下列计算正确的是( )
A. a3+a2=2a5 B. (﹣2a3)2=4a6 C. (a+b)2=a2+b2 D. a6÷a2=a3
解答: 解:A、a3和a2不是同类项不能合并,故本选项错误;B、(﹣2a3)2=4a6,正确;C、应为(a+b)2=a2+b2+2ab,故本选项错误;D、应为a6÷a2=a4,故本选项错误.故选B.
2.若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是( )
A. x+y+z=0 B. x+y﹣2z=0 C. y+z﹣2x=0 D. z+x﹣2y=0
解答: 解:∵(x﹣z)2﹣4(x﹣y)(y﹣z)=0,∴x2+z2﹣2xz﹣4xy+4xz+4y2﹣4yz=0,∴x2+z2+2xz﹣4xy+4y2﹣4yz=0,∴(x+z)2﹣4y(x+z)+4y2=0,∴(x+z﹣2y)2=0,∴z+x﹣2y=0.故选D.
3.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )
A. 40° B. 60° C. 80° D. 120°
解答: 解:∵a∥b,∴∠1=∠2+∠3,∵∠1=120°,∠2=80°,∴∠3=120°﹣80°=40°,故选A.
4.恩施生态旅游初步形成,2011年全年实现旅游综合收入9 086 600 000元.数9 086 600 000用科学记数法表示(保留三个有效数字),正确的是( )
A. 9.09×109 B. 9.087×1010 C. 9.08×109 D. 9.09×108
解答: 解:9 086 600 000=9.0866×109≈9.09×109故选A.
5.如图,有四张不透明的卡片除正面的算式不同外,其余完全相同,将它们背面朝上洗匀后,从中随机抽取一张,则抽到得卡片上算式正确的概率是( )
A. B. C. D. 1
解答: 解:四张卡片中第一张和第三张正确,∵四张卡片中有两张正确,故随机抽取一张,则抽到得卡片上算式正确的概率是=,故选B.
6.如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( )
A. 100° B. 80° C. 70° D. 50°
解答: 解:延长BD交AC于E.∵DA=DB=DC,∴∠ABE=∠DAB=20°,∠ECD=∠DAC=30°.又∵∠BAE=∠BAD+∠DAC=50°,∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,∴∠BDC=∠ABE+∠BAE+∠ECD=20°+50°+30°=100°.故选A.
7.用固定的速度如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是
( )
A. B. C. D.
解答: 解:因瓶子下面窄上面宽,且相同的时间内注入的水量相同,所以下面的高度增加的快,上面增加的慢,即图象应越来越缓,分析四个图象只有C符合要求.故选C.
8.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( )
A. 10 B. 8 C. 5 D. 2.5
解答: 解:∵DE是线段BC的垂直平分线,∴BE=CE,∠BDE=90°(线段垂直平分线的性质),∵∠B=30°,∴BE=2DE=2×5=10(直角三角形的性质),∴CE=BE=10.故选A.
9.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A. PO B. PQ C. MO D. MQ
解答: 解:要想利用△PQO≌△NMO求得MN的长,只需求得线段PQ的长,故选B.
10.利用基本尺规作图,下列条件中,不能作出唯一直角三角形的是( )
A. 已知斜边和一锐角 B. 已知一直角边和一锐角
C. 已知斜边和一直角边 D. 已知两个锐角
解答: 解:A、符合全等三角形的判定AAS,能作出唯一直角三角形;B、符合全等三角形的判定SAS,能作出唯一直角三角形;C、符合全等三角形的判定HL,能作出唯一直角三角形;D、因为已知两个锐角,而边长不确定,故这样的三角形可作很多,而不是唯一的故选D.
11.已知:如图,点D、E分别在AB、AC边上,△ABE≌△ACD,AC=15,BD=9,则线段AD的长是( )
A. 6 B. 9 C. 12 D. 15
解答: 解:∵△ABE≌△ACD,∴AD=AE,AB=AC=15,∴AD=AB﹣BD=15﹣9=6.故选A.
12.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A. 21 B. 28 C. 36 D. 45
解答: 解:观察图形可得:n条直线相交最多可形成的交点个数为,∴8条直线相交,最多可形成交点的个数为====28.故选B.
二.填空题(共6小题)
13.设a>b>0,a2+b2﹣6ab=0,则()2的值等于 2 .
解答: 解:由a2+b2﹣6ab=0可得(b﹣a)2=4ab,﹣﹣﹣﹣①;(a+b)2=8ab,﹣﹣﹣②;②÷①得=2,由a>b>0,可得<0,故=﹣.故答案为:﹣.
14.如图,CD⊥AB,垂足为C,∠1=130°,则∠2= 40 度.
解答: 解:由图知,∠1和∠ACE是对顶角,∴∠1=∠ACE=130°,即∠ACD+∠2=130°,∵CD⊥AB,∴∠ACD=90°,∴130°=90°+∠2,解得∠2=40°.
15. 2011年湛江市社会经济实现快速发展,全市城镇居民全年可支配收入约为17000元,数据17000用科学记数法表示为 1.7×104 .(保留两位有效数字)
解答: 解:17000=1.7×104≈1.7×104.故答案为:1.7×104
16.掷一枚质地均匀的骰子,骰子的六个面上分别标有数字1~6,掷得朝上的一面的数字为奇数的概率是 .
解答: 解:正方体骰子,六个面上分别刻有的1,2,3,4,5,6六个数字中,奇数为1,3,5,则向上一面的数字是奇数的概率为=.故答案为:.
17.在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是 ①②④ .
解答: 解:①在△ADB和△ADC中,AD=AD,若添加条件BD=DC,AB=AC,根据全等三角形的判定定理SSS可以证得△ADB≌△ADC;故本选项正确;②在△ADB和△ADC中,AD=AD,若添加条件∠B=∠C,∠BAD=∠CAD,根据全等三角形的判定定理AAS可以证得△ADB≌△ADC;故本选项正确;③在△ADB和△ADC中,AD=AD,若添加条件∠B=∠C,BD=DC,由SSA不可以证得△ADB≌△ADC;故本选项错误;④在△ADB和△ADC中,AD=AD,若添加条件∠ADB=∠ADC,BD=DC,根据全等三角形的判定定理SAS可以证得△ADB≌△ADC;故本选项正确;综上所述,符合题意的序号是①②④;故答案是:①②④.
18.五一节某超市搞促销活动:①一次性购物不超过150元不享受优惠;②一次性购物超过150元但不超过500元一律九折;③一次性购物超过500元一律八折.王宁两次购物分别付款120元、432元,若王宁一次性购买与上两次相同的商品,则应付款 480元或528 元.
解答: 解:一次性购物超过150元,但不超过500元一律9折则在这个范围内最低付款135元,因而第一次付款120元,没有优惠;第二次购物时:是第二种优惠,可得出原价是432÷0.9=480(符合超过150不高于500).则两次共付款:120+480=600元,超过500元,则一次性购买应付款:600×0.8=480元;当第二次付款是超过500元时:可得出原价是 432÷0.8=540(符合超过500元),则两次共应付款:120+540=660元,则一次性购买应付款:660×0.8=528元.则一次性购买应付款:480元或528元.故答案是:480元或528.
三.解答题(共8小题)
19.计算:
解答: 解:由题意可设字母n=12346,那么12345=n﹣1,12347=n+1,于是分母变为n2﹣(n﹣1)(n+1).应用平方差公式化简得n2﹣(n2﹣12)=n2﹣n2+1=1,即原式分母的值是1,所以原式=24690.
20.某位同学做一道题:已知两个多项式A、B,求A﹣B的值.他误将A﹣B看成A+B,求得结果为3x2﹣3x+5,已知B=x2﹣x﹣1.
(1)求多项式A;
(2)求A﹣B的正确答案.
解答: 解:(1)由已知,A+B=3x2﹣3x+5,则A=3x2﹣3x+5﹣(x2﹣x﹣1),=3x2﹣3x+5﹣x2+x+1,=2x2﹣2x+6.(2)A﹣B=2x2﹣2x+6﹣(x2﹣x﹣1),=2x2﹣2x+6﹣x2+x+1,=x2﹣x+7.
21.先化简,再求值:2x2+(﹣x2+3xy+2y2)﹣( x2﹣xy+2y2),其中 x=,y=3.
解答: 解:原式=2x2﹣x2+3xy+2y2﹣x2+xy﹣2y2,=(2﹣1﹣1)x2+(3+1)xy+(2﹣2)y2,=4xy,当x=,y=3时,原式=4××3=6.
22.如图,直线AB与CD相交于O,OE平分∠AOB,OF平分∠COD.
(1)图中与∠COA互补的角是 ∠AOD或∠COB ;(把符合条件的所有角都写出来)
(2)如果∠AOC=35°,求∠EOF的度数.
解答: 解:(1)图中与∠COA互补的角是∠AOD或∠COB.故答案为:∠AOD或∠COB.(2)∵OE平分∠AOB,OF平分∠COD.∴∠AOE=90°,∠COF=90°,∵∠AOC=35°,∴∠EOF=∠AOE+∠COF﹣∠AOC=90°+90°﹣35°=145°.或∠EOF=∠AOE+∠COF+∠AOC=215°.答:∠EOF为145°或215°.
24.小亮家距离学校8千米,昨天早晨,小亮骑车上学途中,自行车“爆胎”,恰好路边有“自行车”维修部,几分钟后车修好了,为了不迟到,他加快了骑车到校的速度.回校后,小亮根据这段经历画出如下图象.该图象描绘了小亮行的路程S与他所用的时间t之间的关系.请根据图象,解答下列问题:
(1)小亮行了多少千米时,自行车“爆胎”?修车用了几分钟?
(2)小亮到校路上共用了多少时间?
(3)如果自行车没有“爆胎”,一直用修车前的速度行驶,那么他比实际情况早到或晚到学校多少分钟(精确到0.1)?
解答: 解:(1)3千米;修车用了15﹣10=5(分钟);(2分)(2)30分钟;(4分)(3)小亮修车前的速度为(千米/分钟),(5分)按此速度到校共需时间为(分钟),(6分)(分钟),则他比实际情况早到学校3.3分钟.(8分)若用其他做法可参照此标准评分.
25.如图,在△MNP中,∠MNP=45°,H是高MQ和高NR的交点,求证:HN=PM.
解答: 如图1∵MQ⊥PN,∠MNP=45°,∴∠QMN=45°=∠QNM,∴QM=QN,∵NR⊥PM,∴∠1+∠4=90°,又∵∠2+∠3=90°,∠3=∠4,∴∠1=∠2,在△HQN和△PQM中,,∴△HQN≌△PQM(ASA),∴HN=PM.??
26.已知,如图,点D在边BC上,点E在△ABC外部,DE交AC于F,若AD=AB,∠1=∠2=∠3.
求证:BC=DE.
解答: 证明:∵∠1=∠2=∠3,∴∠2+∠DAC=∠1+∠DAC,∴∠BAC=∠DAE,又∵∠DFC=∠AFE,∠3=∠1,∴由三角形的内角和定理得:∠C=∠E,∵在△ABC和△ADE中,∴△ABC≌△ADE(AAS),∴BC=DE.
一.选择题
1.下列计算正确的是( )
A. a3+a2=2a5 B. (﹣2a3)2=4a6 C. (a+b)2=a2+b2 D. a6÷a2=a3
2.若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是( )
A. x+y+z=0 B. x+y﹣2z=0 C. y+z﹣2x=0 D. z+x﹣2y=0
3.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是
A. 40° B. 60° C. 80° D. 120°
3题 6题 8题 9题 11题
4.恩施生态旅游初步形成,2011年全年实现旅游综合收入9 086 600 000元.数9 086 600 000用科学记数法表示(保留三个有效数字),正确的是( )
A. 9.09×109 B. 9.087×1010 C. 9.08×109 D. 9.09×108
5.如图,有四张不透明的卡片除正面的算式不同外,其余完全相同,将它们背面朝上洗匀后,从中随机抽取一张,则抽到得卡片上算式正确的概率是( )
A. B. C. D. 1
6.如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是
A. 100° B. 80° C. 70° D. 50°
7.用固定的速度如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( )
A. B. C. D.
8.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( )
A. 10 B. 8 C. 5 D. 2.5
9.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A. PO B. PQ C. MO D. MQ
10.利用基本尺规作图,下列条件中,不能作出唯一直角三角形的是( )
A. 已知斜边和一锐角 B. 已知一直角边和一锐角
C. 已知斜边和一直角边 D. 已知两个锐角
11.已知:如图,点D、E分别在AB、AC边上,△ABE≌△ACD,AC=15,BD=9,则线段AD的长是( )
A. 6 B. 9 C. 12 D. 15
2.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A. 21 B. 28 C. 36 D. 45
二.填空题(共6小题)
13.设a>b>0,a2+b2﹣6ab=0,则()2的值等于 _________ .
14.如图,CD⊥AB,垂足为C,∠1=130°,则∠2= _________ 度.
15.2011年湛江市社会经济实现快速发展,全市城镇居民全年可支配收入约为17000元,数据17000用科学记数法表示为 _________ .(保留两位有效数字)
16.掷一枚质地均匀的骰子,骰子的六个面上分别标有数字1~6,掷得朝上的一面的数字为奇数的概率是 _________ .
17.在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是_________.
18.五一节某超市搞促销活动:①一次性购物不超过150元不享受优惠;②一次性购物超过150元但不超过500元一律九折;③一次性购物超过500元一律八折.王宁两次购物分别付款120元、432元,若王宁一次性购买与上两次相同的商品,则应付款 _________ 元.
三.解答题(共8小题)
19.计算:
20.某位同学做一道题:已知两个多项式A、B,求A﹣B的值.他误将A﹣B看成A+B,求得结果为3x2﹣3x+5,已知B=x2﹣x﹣1.(1)求多项式A;(2)求A﹣B的正确答案.
21.先化简,再求值:2x2+(﹣x2+3xy+2y2)﹣( x2﹣xy+2y2),其中 x=,y=3.
22.如图,直线AB与CD相交于O,OE平分∠AOB,OF平分∠COD.
(1)图中与∠COA互补的角是 _________ ;(把符合条件的所有角都写出来)
(2)如果∠AOC=35°,求∠EOF的度数.
24.小亮家距离学校8千米,昨天早晨,小亮骑车上学途中,自行车“爆胎”,恰好路边有“自行车”维修部,几分钟后车修好了,为了不迟到,他加快了骑车到校的速度.回校后,小亮根据这段经历画出如下图象.该图象描绘了小亮行的路程S与他所用的时间t之间的关系.请根据图象,解答下列问题:
(1)小亮行了多少千米时,自行车“爆胎”?修车用了几分钟?
(2)小亮到校路上共用了多少时间?
(3)如果自行车没有“爆胎”,一直用修车前的速度行驶,那么他比实际情况早到或晚到学校多少分钟(精确到0.1)?
25.如图,在△MNP中,∠MNP=45°,H是高MQ和高NR的交点,求证:HN=PM.
26.已知,如图,点D在边BC上,点E在△ABC外部,DE交AC于F,若AD=AB,∠1=∠2=∠3.
求证:BC=DE.
2013~2014年度大庆市房顶中学初二期末测试卷
参考答案与试题解析
一.选择题(共12小题)
1.下列计算正确的是( )
A. a3+a2=2a5 B. (﹣2a3)2=4a6 C. (a+b)2=a2+b2 D. a6÷a2=a3
解答: 解:A、a3和a2不是同类项不能合并,故本选项错误;B、(﹣2a3)2=4a6,正确;C、应为(a+b)2=a2+b2+2ab,故本选项错误;D、应为a6÷a2=a4,故本选项错误.故选B.
2.若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是( )
A. x+y+z=0 B. x+y﹣2z=0 C. y+z﹣2x=0 D. z+x﹣2y=0
解答: 解:∵(x﹣z)2﹣4(x﹣y)(y﹣z)=0,∴x2+z2﹣2xz﹣4xy+4xz+4y2﹣4yz=0,∴x2+z2+2xz﹣4xy+4y2﹣4yz=0,∴(x+z)2﹣4y(x+z)+4y2=0,∴(x+z﹣2y)2=0,∴z+x﹣2y=0.故选D.
3.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )
A. 40° B. 60° C. 80° D. 120°
解答: 解:∵a∥b,∴∠1=∠2+∠3,∵∠1=120°,∠2=80°,∴∠3=120°﹣80°=40°,故选A.
4.恩施生态旅游初步形成,2011年全年实现旅游综合收入9 086 600 000元.数9 086 600 000用科学记数法表示(保留三个有效数字),正确的是( )
A. 9.09×109 B. 9.087×1010 C. 9.08×109 D. 9.09×108
解答: 解:9 086 600 000=9.0866×109≈9.09×109故选A.
5.如图,有四张不透明的卡片除正面的算式不同外,其余完全相同,将它们背面朝上洗匀后,从中随机抽取一张,则抽到得卡片上算式正确的概率是( )
A. B. C. D. 1
解答: 解:四张卡片中第一张和第三张正确,∵四张卡片中有两张正确,故随机抽取一张,则抽到得卡片上算式正确的概率是=,故选B.
6.如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( )
A. 100° B. 80° C. 70° D. 50°
解答: 解:延长BD交AC于E.∵DA=DB=DC,∴∠ABE=∠DAB=20°,∠ECD=∠DAC=30°.又∵∠BAE=∠BAD+∠DAC=50°,∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,∴∠BDC=∠ABE+∠BAE+∠ECD=20°+50°+30°=100°.故选A.
7.用固定的速度如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是
( )
A. B. C. D.
解答: 解:因瓶子下面窄上面宽,且相同的时间内注入的水量相同,所以下面的高度增加的快,上面增加的慢,即图象应越来越缓,分析四个图象只有C符合要求.故选C.
8.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( )
A. 10 B. 8 C. 5 D. 2.5
解答: 解:∵DE是线段BC的垂直平分线,∴BE=CE,∠BDE=90°(线段垂直平分线的性质),∵∠B=30°,∴BE=2DE=2×5=10(直角三角形的性质),∴CE=BE=10.故选A.
9.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A. PO B. PQ C. MO D. MQ
解答: 解:要想利用△PQO≌△NMO求得MN的长,只需求得线段PQ的长,故选B.
10.利用基本尺规作图,下列条件中,不能作出唯一直角三角形的是( )
A. 已知斜边和一锐角 B. 已知一直角边和一锐角
C. 已知斜边和一直角边 D. 已知两个锐角
解答: 解:A、符合全等三角形的判定AAS,能作出唯一直角三角形;B、符合全等三角形的判定SAS,能作出唯一直角三角形;C、符合全等三角形的判定HL,能作出唯一直角三角形;D、因为已知两个锐角,而边长不确定,故这样的三角形可作很多,而不是唯一的故选D.
11.已知:如图,点D、E分别在AB、AC边上,△ABE≌△ACD,AC=15,BD=9,则线段AD的长是( )
A. 6 B. 9 C. 12 D. 15
解答: 解:∵△ABE≌△ACD,∴AD=AE,AB=AC=15,∴AD=AB﹣BD=15﹣9=6.故选A.
12.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A. 21 B. 28 C. 36 D. 45
解答: 解:观察图形可得:n条直线相交最多可形成的交点个数为,∴8条直线相交,最多可形成交点的个数为====28.故选B.
二.填空题(共6小题)
13.设a>b>0,a2+b2﹣6ab=0,则()2的值等于 2 .
解答: 解:由a2+b2﹣6ab=0可得(b﹣a)2=4ab,﹣﹣﹣﹣①;(a+b)2=8ab,﹣﹣﹣②;②÷①得=2,由a>b>0,可得<0,故=﹣.故答案为:﹣.
14.如图,CD⊥AB,垂足为C,∠1=130°,则∠2= 40 度.
解答: 解:由图知,∠1和∠ACE是对顶角,∴∠1=∠ACE=130°,即∠ACD+∠2=130°,∵CD⊥AB,∴∠ACD=90°,∴130°=90°+∠2,解得∠2=40°.
15. 2011年湛江市社会经济实现快速发展,全市城镇居民全年可支配收入约为17000元,数据17000用科学记数法表示为 1.7×104 .(保留两位有效数字)
解答: 解:17000=1.7×104≈1.7×104.故答案为:1.7×104
16.掷一枚质地均匀的骰子,骰子的六个面上分别标有数字1~6,掷得朝上的一面的数字为奇数的概率是 .
解答: 解:正方体骰子,六个面上分别刻有的1,2,3,4,5,6六个数字中,奇数为1,3,5,则向上一面的数字是奇数的概率为=.故答案为:.
17.在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是 ①②④ .
解答: 解:①在△ADB和△ADC中,AD=AD,若添加条件BD=DC,AB=AC,根据全等三角形的判定定理SSS可以证得△ADB≌△ADC;故本选项正确;②在△ADB和△ADC中,AD=AD,若添加条件∠B=∠C,∠BAD=∠CAD,根据全等三角形的判定定理AAS可以证得△ADB≌△ADC;故本选项正确;③在△ADB和△ADC中,AD=AD,若添加条件∠B=∠C,BD=DC,由SSA不可以证得△ADB≌△ADC;故本选项错误;④在△ADB和△ADC中,AD=AD,若添加条件∠ADB=∠ADC,BD=DC,根据全等三角形的判定定理SAS可以证得△ADB≌△ADC;故本选项正确;综上所述,符合题意的序号是①②④;故答案是:①②④.
18.五一节某超市搞促销活动:①一次性购物不超过150元不享受优惠;②一次性购物超过150元但不超过500元一律九折;③一次性购物超过500元一律八折.王宁两次购物分别付款120元、432元,若王宁一次性购买与上两次相同的商品,则应付款 480元或528 元.
解答: 解:一次性购物超过150元,但不超过500元一律9折则在这个范围内最低付款135元,因而第一次付款120元,没有优惠;第二次购物时:是第二种优惠,可得出原价是432÷0.9=480(符合超过150不高于500).则两次共付款:120+480=600元,超过500元,则一次性购买应付款:600×0.8=480元;当第二次付款是超过500元时:可得出原价是 432÷0.8=540(符合超过500元),则两次共应付款:120+540=660元,则一次性购买应付款:660×0.8=528元.则一次性购买应付款:480元或528元.故答案是:480元或528.
三.解答题(共8小题)
19.计算:
解答: 解:由题意可设字母n=12346,那么12345=n﹣1,12347=n+1,于是分母变为n2﹣(n﹣1)(n+1).应用平方差公式化简得n2﹣(n2﹣12)=n2﹣n2+1=1,即原式分母的值是1,所以原式=24690.
20.某位同学做一道题:已知两个多项式A、B,求A﹣B的值.他误将A﹣B看成A+B,求得结果为3x2﹣3x+5,已知B=x2﹣x﹣1.
(1)求多项式A;
(2)求A﹣B的正确答案.
解答: 解:(1)由已知,A+B=3x2﹣3x+5,则A=3x2﹣3x+5﹣(x2﹣x﹣1),=3x2﹣3x+5﹣x2+x+1,=2x2﹣2x+6.(2)A﹣B=2x2﹣2x+6﹣(x2﹣x﹣1),=2x2﹣2x+6﹣x2+x+1,=x2﹣x+7.
21.先化简,再求值:2x2+(﹣x2+3xy+2y2)﹣( x2﹣xy+2y2),其中 x=,y=3.
解答: 解:原式=2x2﹣x2+3xy+2y2﹣x2+xy﹣2y2,=(2﹣1﹣1)x2+(3+1)xy+(2﹣2)y2,=4xy,当x=,y=3时,原式=4××3=6.
22.如图,直线AB与CD相交于O,OE平分∠AOB,OF平分∠COD.
(1)图中与∠COA互补的角是 ∠AOD或∠COB ;(把符合条件的所有角都写出来)
(2)如果∠AOC=35°,求∠EOF的度数.
解答: 解:(1)图中与∠COA互补的角是∠AOD或∠COB.故答案为:∠AOD或∠COB.(2)∵OE平分∠AOB,OF平分∠COD.∴∠AOE=90°,∠COF=90°,∵∠AOC=35°,∴∠EOF=∠AOE+∠COF﹣∠AOC=90°+90°﹣35°=145°.或∠EOF=∠AOE+∠COF+∠AOC=215°.答:∠EOF为145°或215°.
24.小亮家距离学校8千米,昨天早晨,小亮骑车上学途中,自行车“爆胎”,恰好路边有“自行车”维修部,几分钟后车修好了,为了不迟到,他加快了骑车到校的速度.回校后,小亮根据这段经历画出如下图象.该图象描绘了小亮行的路程S与他所用的时间t之间的关系.请根据图象,解答下列问题:
(1)小亮行了多少千米时,自行车“爆胎”?修车用了几分钟?
(2)小亮到校路上共用了多少时间?
(3)如果自行车没有“爆胎”,一直用修车前的速度行驶,那么他比实际情况早到或晚到学校多少分钟(精确到0.1)?
解答: 解:(1)3千米;修车用了15﹣10=5(分钟);(2分)(2)30分钟;(4分)(3)小亮修车前的速度为(千米/分钟),(5分)按此速度到校共需时间为(分钟),(6分)(分钟),则他比实际情况早到学校3.3分钟.(8分)若用其他做法可参照此标准评分.
25.如图,在△MNP中,∠MNP=45°,H是高MQ和高NR的交点,求证:HN=PM.
解答: 如图1∵MQ⊥PN,∠MNP=45°,∴∠QMN=45°=∠QNM,∴QM=QN,∵NR⊥PM,∴∠1+∠4=90°,又∵∠2+∠3=90°,∠3=∠4,∴∠1=∠2,在△HQN和△PQM中,,∴△HQN≌△PQM(ASA),∴HN=PM.??
26.已知,如图,点D在边BC上,点E在△ABC外部,DE交AC于F,若AD=AB,∠1=∠2=∠3.
求证:BC=DE.
解答: 证明:∵∠1=∠2=∠3,∴∠2+∠DAC=∠1+∠DAC,∴∠BAC=∠DAE,又∵∠DFC=∠AFE,∠3=∠1,∴由三角形的内角和定理得:∠C=∠E,∵在△ABC和△ADE中,∴△ABC≌△ADE(AAS),∴BC=DE.
同课章节目录
