27.2.1 第1课时 平行线分线段成比例 教案
文档属性
| 名称 | 27.2.1 第1课时 平行线分线段成比例 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
教学目标
【知识与技能】
1.了解相似三角形的概念;
2.掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例;平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.21教育网
3.探索并掌握相似三角形的判定方法——平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.www.21-cn-jy.com
【过程与方法】
经历平行线分线段成比例定理的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程.
【情感、态度与价值观】
通过画图、度量等操作,培养学生获得数学猜想的经验,激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.【来源:21·世纪·教育·网】
教学重难点
【教学重点】
平行线分线段成比例定理及判定三角形相似的定理.
【教学难点】
判定三角形相似的定理的应用.
教学过程
一、情境导入
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界七大奇迹之一”.塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米.据考证,为建成大金字塔,共动用了约10万人花了近20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀,所以高度有所降低.21世纪教育网版权所有
在古希腊,有一位伟大的科学家叫泰勒斯.一天,希腊国王阿马西斯对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”这在当时条件下是个大难题,因为是很难爬到塔顶的.你知道泰勒斯是怎样测量大金字塔的高度的吗 21·cn·jy·com
二、合作探究
探究点1 相似三角形及其相似比
典例1 下列各组三角形一定相似的是 ( )
A.两个直角三角形
B.两个钝角三角形
C.两个等腰三角形
D.两个等边三角形
[解析] 两个等边三角形各个角都相等,各边对应成比例.
[答案] D
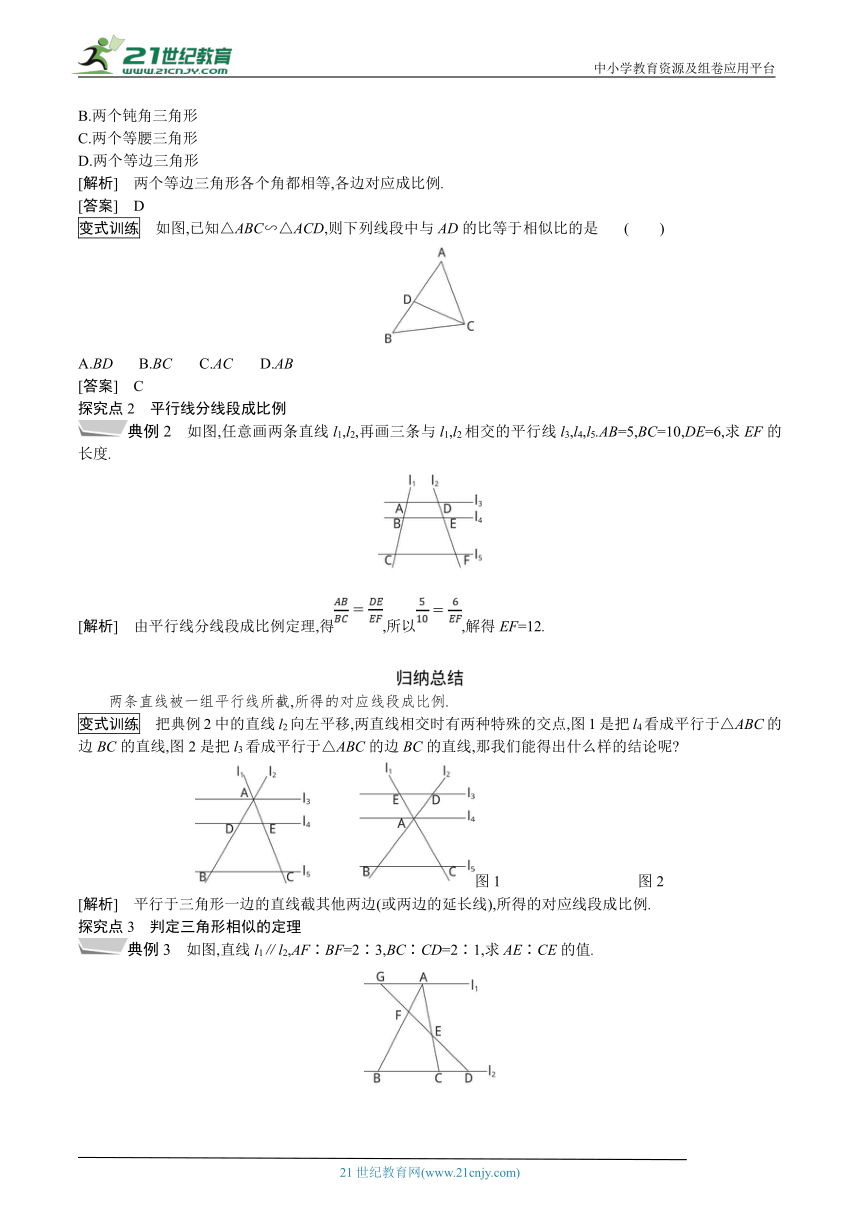
变式训练 如图,已知△ABC∽△ACD,则下列线段中与AD的比等于相似比的是 ( )
A.BD B.BC C.AC D.AB
[答案] C
探究点2 平行线分线段成比例
典例2 如图,任意画两条直线l1,l2,再画三条与l1,l2相交的平行线l3,l4,l5.AB=5,BC=10,DE=6,求EF的长度.21cnjy.com
[解析] 由平行线分线段成比例定理,得,所以,解得EF=12.
两条直线被一组平行线所截,所得的对应线段成比例.
变式训练 把典例2中的直线l2向左平移,两直线相交时有两种特殊的交点,图1是把l4看成平行于△ABC的边BC的直线,图2是把l3看成平行于△ABC的边BC的直线,那我们能得出什么样的结论呢
图1 图2
[解析] 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
探究点3 判定三角形相似的定理
典例3 如图,直线l1∥l2,AF∶BF=2∶3,BC∶CD=2∶1,求AE∶CE的值.
[解析] ∵l1∥l2,
∴△AGF∽△BDF,△AGE∽△CDE,
∴,∴AG=BD.
又∵,BC+CD=BD,∴CD=BD,
∴=2,即AE∶EC=2.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
变式训练 如图所示,∠ADE=∠ACD=∠ABC,图中相似三角形共有 ( )
A.1对 B.2对
C.3对 D.4对
[答案] D
三、板书设计
平行线分线段成比例
1.相似三角形的概念:
三个角分别相等,三条边成比例的两个三角形叫相似三角形.相似三角形的对应边的比叫做相似比.
2.平行线分线段成比例:
两条直线被一组平行线所截,所得的对应线段成比例;平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.2·1·c·n·j·y
3.判定三角形相似的定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
教学反思
相似三角形是全等三角形的拓广和发展,在这之前,学生已经学习了全等三角形的相关知识,这为学生继续研究相似三角形奠定了基础.相似三角形的判定是进一步对相似三角形的本质和定义的全面研究,也是以后研究圆中比例线段和三角函数的重要工具.21·世纪*教育网
本节课先介绍平行线分线段成比例的基本事实,然后将这个基本事实应用到三角形上得到了一个推论,最后利用这个推论并通过三角形中平行线段证明两个三角形相似.www-2-1-cnjy-com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
教学目标
【知识与技能】
1.了解相似三角形的概念;
2.掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例;平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.21教育网
3.探索并掌握相似三角形的判定方法——平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.www.21-cn-jy.com
【过程与方法】
经历平行线分线段成比例定理的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程.
【情感、态度与价值观】
通过画图、度量等操作,培养学生获得数学猜想的经验,激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.【来源:21·世纪·教育·网】
教学重难点
【教学重点】
平行线分线段成比例定理及判定三角形相似的定理.
【教学难点】
判定三角形相似的定理的应用.
教学过程
一、情境导入
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界七大奇迹之一”.塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米.据考证,为建成大金字塔,共动用了约10万人花了近20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀,所以高度有所降低.21世纪教育网版权所有
在古希腊,有一位伟大的科学家叫泰勒斯.一天,希腊国王阿马西斯对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”这在当时条件下是个大难题,因为是很难爬到塔顶的.你知道泰勒斯是怎样测量大金字塔的高度的吗 21·cn·jy·com
二、合作探究
探究点1 相似三角形及其相似比
典例1 下列各组三角形一定相似的是 ( )
A.两个直角三角形
B.两个钝角三角形
C.两个等腰三角形
D.两个等边三角形
[解析] 两个等边三角形各个角都相等,各边对应成比例.
[答案] D
变式训练 如图,已知△ABC∽△ACD,则下列线段中与AD的比等于相似比的是 ( )
A.BD B.BC C.AC D.AB
[答案] C
探究点2 平行线分线段成比例
典例2 如图,任意画两条直线l1,l2,再画三条与l1,l2相交的平行线l3,l4,l5.AB=5,BC=10,DE=6,求EF的长度.21cnjy.com
[解析] 由平行线分线段成比例定理,得,所以,解得EF=12.
两条直线被一组平行线所截,所得的对应线段成比例.
变式训练 把典例2中的直线l2向左平移,两直线相交时有两种特殊的交点,图1是把l4看成平行于△ABC的边BC的直线,图2是把l3看成平行于△ABC的边BC的直线,那我们能得出什么样的结论呢
图1 图2
[解析] 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
探究点3 判定三角形相似的定理
典例3 如图,直线l1∥l2,AF∶BF=2∶3,BC∶CD=2∶1,求AE∶CE的值.
[解析] ∵l1∥l2,
∴△AGF∽△BDF,△AGE∽△CDE,
∴,∴AG=BD.
又∵,BC+CD=BD,∴CD=BD,
∴=2,即AE∶EC=2.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
变式训练 如图所示,∠ADE=∠ACD=∠ABC,图中相似三角形共有 ( )
A.1对 B.2对
C.3对 D.4对
[答案] D
三、板书设计
平行线分线段成比例
1.相似三角形的概念:
三个角分别相等,三条边成比例的两个三角形叫相似三角形.相似三角形的对应边的比叫做相似比.
2.平行线分线段成比例:
两条直线被一组平行线所截,所得的对应线段成比例;平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.2·1·c·n·j·y
3.判定三角形相似的定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
教学反思
相似三角形是全等三角形的拓广和发展,在这之前,学生已经学习了全等三角形的相关知识,这为学生继续研究相似三角形奠定了基础.相似三角形的判定是进一步对相似三角形的本质和定义的全面研究,也是以后研究圆中比例线段和三角函数的重要工具.21·世纪*教育网
本节课先介绍平行线分线段成比例的基本事实,然后将这个基本事实应用到三角形上得到了一个推论,最后利用这个推论并通过三角形中平行线段证明两个三角形相似.www-2-1-cnjy-com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
