29.2 第2课时 由三视图确定几何体 教案
文档属性
| 名称 | 29.2 第2课时 由三视图确定几何体 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 20:21:59 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
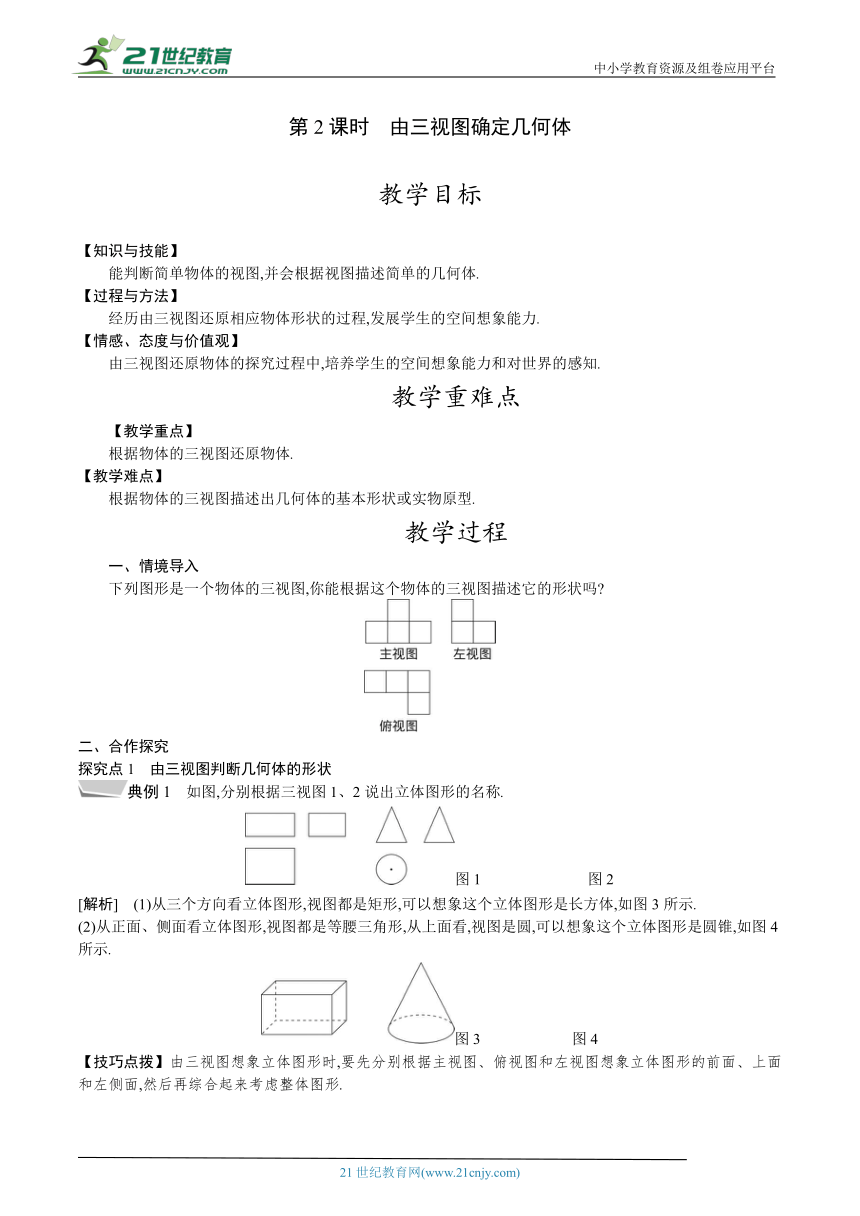
第2课时 由三视图确定几何体
教学目标
【知识与技能】
能判断简单物体的视图,并会根据视图描述简单的几何体.
【过程与方法】
经历由三视图还原相应物体形状的过程,发展学生的空间想象能力.
【情感、态度与价值观】
由三视图还原物体的探究过程中,培养学生的空间想象能力和对世界的感知.
教学重难点
【教学重点】
根据物体的三视图还原物体.
【教学难点】
根据物体的三视图描述出几何体的基本形状或实物原型.
教学过程
一、情境导入
下列图形是一个物体的三视图,你能根据这个物体的三视图描述它的形状吗
二、合作探究
探究点1 由三视图判断几何体的形状
典例1 如图,分别根据三视图1、2说出立体图形的名称.
图1 图2
[解析] (1)从三个方向看立体图形,视图都是矩形,可以想象这个立体图形是长方体,如图3所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形,从上面看,视图是圆,可以想象这个立体图形是圆锥,如图4所示.21世纪教育网版权所有
图3 图4
【技巧点拨】由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.21教育网
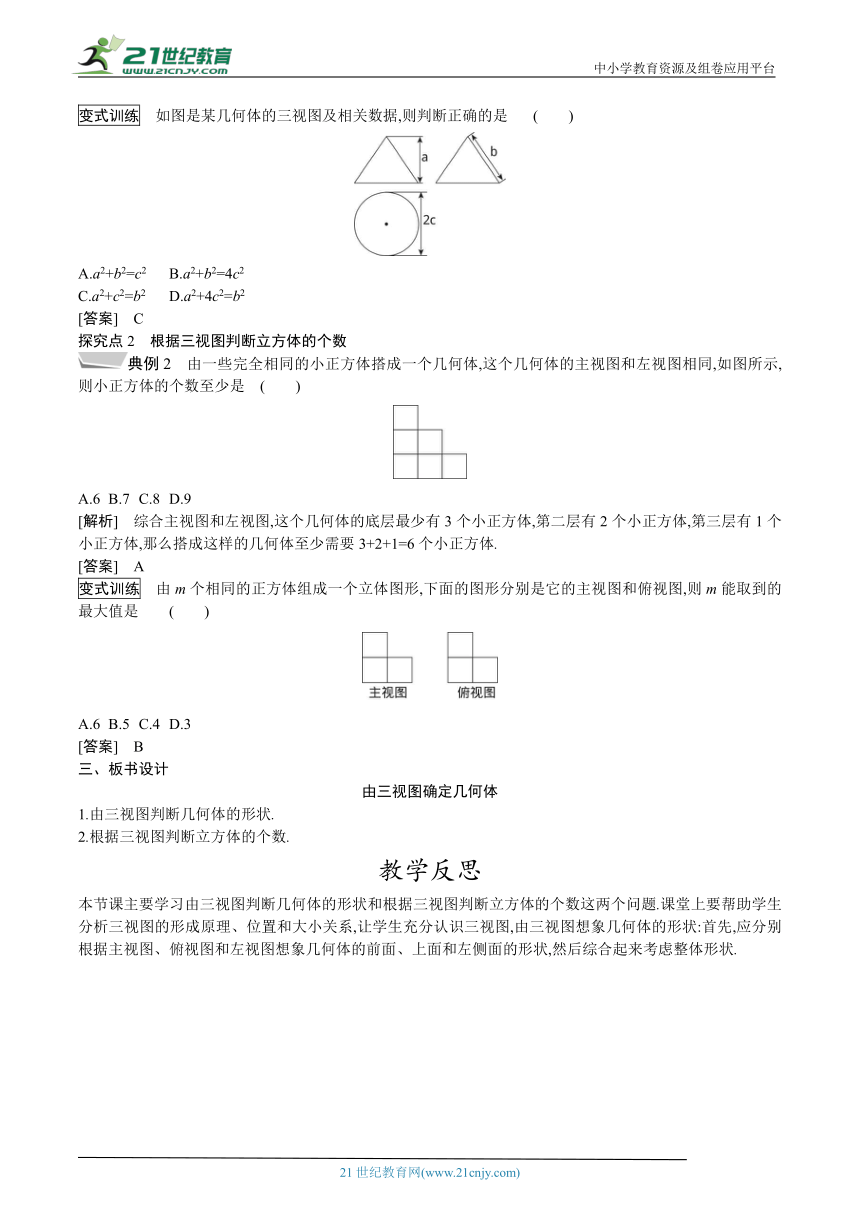
变式训练 如图是某几何体的三视图及相关数据,则判断正确的是 ( )
A.a2+b2=c2 B.a2+b2=4c2
C.a2+c2=b2 D.a2+4c2=b2
[答案] C
探究点2 根据三视图判断立方体的个数
典例2 由一些完全相同的小正方体搭成一个几何体,这个几何体的主视图和左视图相同,如图所示,则小正方体的个数至少是 ( )21cnjy.com
A.6 B.7 C.8 D.9
[解析] 综合主视图和左视图,这个几何体的底层最少有3个小正方体,第二层有2个小正方体,第三层有1个小正方体,那么搭成这样的几何体至少需要3+2+1=6个小正方体.21·cn·jy·com
[答案] A
变式训练 由m个相同的正方体组成一个立体图形,下面的图形分别是它的主视图和俯视图,则m能取到的最大值是 ( )www.21-cn-jy.com
A.6 B.5 C.4 D.3
[答案] B
三、板书设计
由三视图确定几何体
1.由三视图判断几何体的形状.
2.根据三视图判断立方体的个数.
教学反思
本节课主要学习由三视图判断几何体的形状和根据三视图判断立方体的个数这两个问题.课堂上要帮助学生分析三视图的形成原理、位置和大小关系,让学生充分认识三视图,由三视图想象几何体的形状:首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第2课时 由三视图确定几何体
教学目标
【知识与技能】
能判断简单物体的视图,并会根据视图描述简单的几何体.
【过程与方法】
经历由三视图还原相应物体形状的过程,发展学生的空间想象能力.
【情感、态度与价值观】
由三视图还原物体的探究过程中,培养学生的空间想象能力和对世界的感知.
教学重难点
【教学重点】
根据物体的三视图还原物体.
【教学难点】
根据物体的三视图描述出几何体的基本形状或实物原型.
教学过程
一、情境导入
下列图形是一个物体的三视图,你能根据这个物体的三视图描述它的形状吗
二、合作探究
探究点1 由三视图判断几何体的形状
典例1 如图,分别根据三视图1、2说出立体图形的名称.
图1 图2
[解析] (1)从三个方向看立体图形,视图都是矩形,可以想象这个立体图形是长方体,如图3所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形,从上面看,视图是圆,可以想象这个立体图形是圆锥,如图4所示.21世纪教育网版权所有
图3 图4
【技巧点拨】由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.21教育网
变式训练 如图是某几何体的三视图及相关数据,则判断正确的是 ( )
A.a2+b2=c2 B.a2+b2=4c2
C.a2+c2=b2 D.a2+4c2=b2
[答案] C
探究点2 根据三视图判断立方体的个数
典例2 由一些完全相同的小正方体搭成一个几何体,这个几何体的主视图和左视图相同,如图所示,则小正方体的个数至少是 ( )21cnjy.com
A.6 B.7 C.8 D.9
[解析] 综合主视图和左视图,这个几何体的底层最少有3个小正方体,第二层有2个小正方体,第三层有1个小正方体,那么搭成这样的几何体至少需要3+2+1=6个小正方体.21·cn·jy·com
[答案] A
变式训练 由m个相同的正方体组成一个立体图形,下面的图形分别是它的主视图和俯视图,则m能取到的最大值是 ( )www.21-cn-jy.com
A.6 B.5 C.4 D.3
[答案] B
三、板书设计
由三视图确定几何体
1.由三视图判断几何体的形状.
2.根据三视图判断立方体的个数.
教学反思
本节课主要学习由三视图判断几何体的形状和根据三视图判断立方体的个数这两个问题.课堂上要帮助学生分析三视图的形成原理、位置和大小关系,让学生充分认识三视图,由三视图想象几何体的形状:首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
