15.1.1 从分数到分式 课件 (共31张PPT)
文档属性
| 名称 | 15.1.1 从分数到分式 课件 (共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 19:02:43 | ||
图片预览









文档简介
(共31张PPT)
15.1.1 从分数到分式
第十五章 分式
学 习 目 标 1.理解并掌握分式的概念.
2.理解分式有意义的条件及分式值为零的条件.
3.能熟练地求出分式有意义的条件及分式的值为零的条件.
重 点
理解分式有意义的条件及分式值为零的条件.
难 点
能熟练地求出分式有意义的条件及分式的值为零的条件.
1.下列两个整数相除如何表示成分数的形式:
3÷4= 10÷3= 12÷11= -7÷2= -
2.在代数式中,整式的除法是否也能类似地表示?试用类似分数的形式表示下列整式的除法:
(1) 90÷x 可以用式子( )来表示;60÷(x-6)可以用式子( )来表示.
(2) n 公顷麦田共收小麦 m 吨,平均每公顷产量可以用式子( )吨来表示.
一 温故知新 引入课题
章前引言
一艘轮船在静水中的最大航速为30km/h,它以最大船速沿江顺流航行90km所用时间,与以最大航速逆流航行60km所用的时间相等,江水的流速是多少?
如果设江水的流速为vkm/h,则轮船顺流航行90km所用时间为_________h,逆流航行60km所用时间为_________h,由方程_________________可以解出 v 的值.
填空:
(1)长方形的面积为10cm2,长为7cm,则宽为____cm;长方形的面积为S,长为a,宽应为______.
(2)把体积为200cm3的水倒入底面积为33cm2的圆柱形容器中,则水面高度为______cm;把体积为V的水倒入底面积为S的圆柱形容器中,则水面高度为_____.
二 探索交流 发现新知
式子 , , , , , , ,有什么共同点?
它们与分数有什么相同点和不同点?
可以发现,这些式子与分数一样都是 (即A÷B)的形式.
分数的分子A与分母B都是整数,而这些式子中的A,B都是整式,并且B中都含有字母.
二 探索交流 发现新知
一般地,如果A、B都表示两个整式,并且B中含有字母,那么式子 叫做分式.其中A叫做分式的分子,B为分式的分母.
(1)分式是不同于整式的另一类式子.
(2)分母中含有字母是分式的一大特点.
(3)分式比分数更具有一般性. 例如,分数 仅表示2÷3的商,而分式 既可以表示2÷3,又可以表示(-5)÷2,8÷(-9)等.
二 探索交流 发现新知
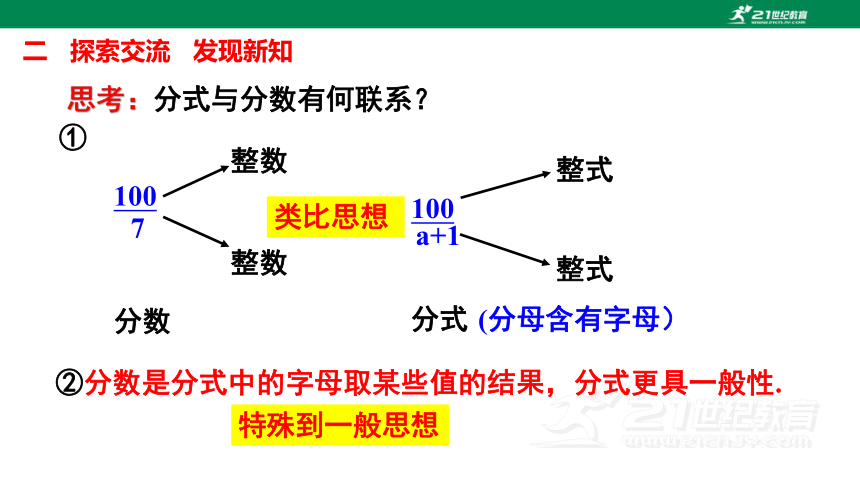
思考:分式与分数有何联系?
②分数是分式中的字母取某些值的结果,分式更具一般性.
整数
整数
整式
整式
(分母含有字母)
分数
分式
类比思想
特殊到一般思想
①
7
100
a+1
100
二 探索交流 发现新知
整数
分数
整式
分式
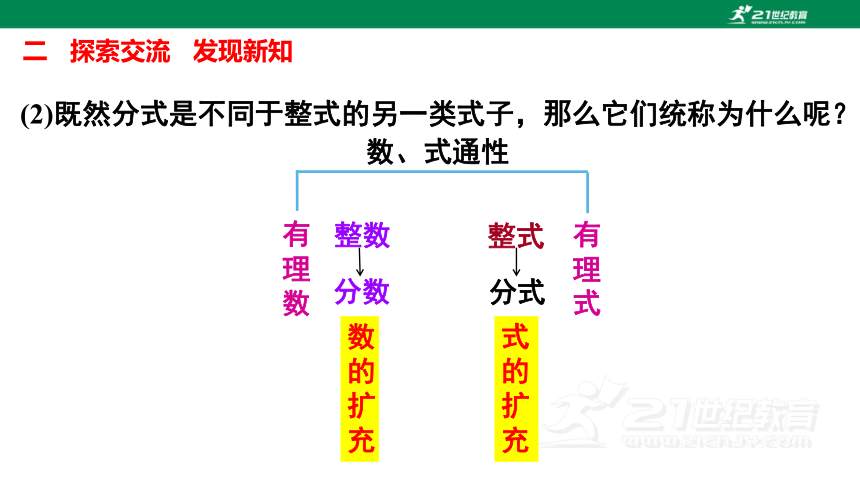
有理数
有理式
数、式通性
(2)既然分式是不同于整式的另一类式子,那么它们统称为什么呢?
数的扩充
式的扩充
二 探索交流 发现新知
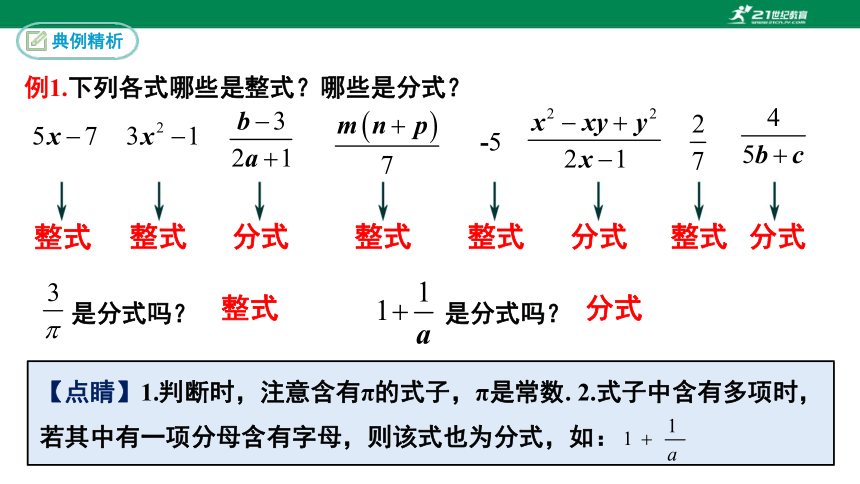
例1.下列各式哪些是整式?哪些是分式?
整式
整式
分式
整式
分式
整式
分式
整式
是分式吗?
是分式吗?
整式
分式
【点睛】1.判断时,注意含有π的式子,π是常数. 2.式子中含有多项时,若其中有一项分母含有字母,则该式也为分式,如:
典例精析
我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,
即当B≠0时,分式 才有意义.
分式有意义的条件
二 探索交流 发现新知
例2.下列分式中的字母满足什么条件时分式有意义?
解:(1)要使分式 有意义,则分母3x≠0,即x≠0;
(2)要使分式 有意义,则分母x-1≠0,即x≠1;
(3)要使分式 有意义,则分母5-3b≠0,即b≠ ;
(4)要使分式 有意义,则分母x-y≠0,即x≠y.
典例精析
例3.已知分式 有意义,则x应满足的条件是 ( )
A.x≠1 B.x≠2
C.x≠1且x≠2 D.以上结果都不对
C
【点睛】分式有意义的条件是分母不为零.如果分母是几个因式乘积的
形式,则每个因式都不为零.
典例精析
1.下列分式中的字母满足什么条件时分式有意义?
针对练习
下列各式中,无论x取何值时,分式都有意义的( )
D
针对练习
分式 的值为零应满足什么条件?分式 的值为正(负)应满足什么条件?
根据除法的意义及法则很容易得到:
1.当A=0且B≠0时,分式 的值为零.
2. 分式 的值为正时,A,B同号.
3. 分式 的值为负时,A,B异号.
二 探索交流 发现新知
解:当分子等于零而分母不等于零时,分式的值为零.
的值为零.
∴当x = 1时分式
x+1≠0,
则 x2 - 1=0,
例4 当x为何值时,分式 的值为零
典例精析
2.当 时,分式 的值为零.
x=2
【分析】要使分式的值为零,只需分子为零且分母不为零,
∴
解得x=2.
3.若 的值为零,则x= .
【分析】分式的值等于零,应满足分子等于零,同时分母不为零,即
解得x=-3.
-3
针对练习
例5. 已知分式
(2) 当x为何值时,分式的值是负数
(1) 当x为何值时,分式的值为正数
典例精析
例6 分式 的值是整数,求整数x的值.
典例精析
4.若分式的值为正数,则x的取值范围为( )
A.x≥- B.x≤-C.x>-且x≠0 D.x<-
5.若分式的值是负数,则x的取值范围是( )
A.x> B.x> C.x< D.x<
C
B
针对练习
6.(1)当x为何值时,分式 的值为负数
7.(1)分式 的值是整数,求整数x的值
(2)分式 的值是整数,求整数x的值
(2)若 值为正数,则的取值范围是
针对练习
一般地,如果A、B都表示两个整式,并且B中含有字母,那么式子
叫做分式.其中A叫做分式的分子,B为分式的分母.
1.当B≠0时,分式 才有意义.
2.当A=0且B≠0时,分式 的值为零.
3. 分式 的值为正时,A,B同号.
4. 分式 的值为负时,A,B异号.
课堂小结
课堂小结
1.下列各式中,,,,,是分式的有( )
A.0个 B.1个 C.2个 D.3个
2.要使分式有意义,x的取值应满足( )
A.x≠2 B.x≠﹣3 C.x≠2且x≠﹣3 D.x≠2或x≠﹣3
3.不论x取何值时,下列分式总有意义的是( )
A. B. C. D.
C
B
D
针对练习
4.若分式 的值为零,则x的值为( )
A.3或 3 B.3 C. 3 D.9
5.已知,则的值是( )
A.-5 B.5 C.-4 D.4
6.若代数式 的值为0,则x=______;当b=______时,分式无意义.
C
B
-2
-4
针对练习
7.当x的值为___________时,分式的值为负.
8.已知,则______.
9.分式的值是整数,则正整数的值等于___________.
10.观察下列各式:,-,,-,……,则第10个式子为_________.
<1且≠0
2或3或5
针对练习
11.当x为何值时,分式有意义?
解:由题意得,x-1≠0,x+2≠0,
解得x≠1且x≠-2.
12.当为何值时,分式的值为零?
解:∵的值为零
∴且
解得:,
当x=2时,
当x=-2时,,故舍去
综上:x=2
针对练习
13.已知分式,当时,分式的值为0;当时,分式没有意义,求的值.
解:时,分式的值为0,
,
.
时,分式没有意义,
,
.
.
针对练习
14.观察下列各式:
第1个等式:.
第2个等式:.
第3个等式:.
……
根据你发现的规律解答下列问题:
(1)第4个等式为:____________.
(2)写出你猜想的第n个等式:__________________(用含n的等式表示)
针对练习
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
15.1.1 从分数到分式
第十五章 分式
学 习 目 标 1.理解并掌握分式的概念.
2.理解分式有意义的条件及分式值为零的条件.
3.能熟练地求出分式有意义的条件及分式的值为零的条件.
重 点
理解分式有意义的条件及分式值为零的条件.
难 点
能熟练地求出分式有意义的条件及分式的值为零的条件.
1.下列两个整数相除如何表示成分数的形式:
3÷4= 10÷3= 12÷11= -7÷2= -
2.在代数式中,整式的除法是否也能类似地表示?试用类似分数的形式表示下列整式的除法:
(1) 90÷x 可以用式子( )来表示;60÷(x-6)可以用式子( )来表示.
(2) n 公顷麦田共收小麦 m 吨,平均每公顷产量可以用式子( )吨来表示.
一 温故知新 引入课题
章前引言
一艘轮船在静水中的最大航速为30km/h,它以最大船速沿江顺流航行90km所用时间,与以最大航速逆流航行60km所用的时间相等,江水的流速是多少?
如果设江水的流速为vkm/h,则轮船顺流航行90km所用时间为_________h,逆流航行60km所用时间为_________h,由方程_________________可以解出 v 的值.
填空:
(1)长方形的面积为10cm2,长为7cm,则宽为____cm;长方形的面积为S,长为a,宽应为______.
(2)把体积为200cm3的水倒入底面积为33cm2的圆柱形容器中,则水面高度为______cm;把体积为V的水倒入底面积为S的圆柱形容器中,则水面高度为_____.
二 探索交流 发现新知
式子 , , , , , , ,有什么共同点?
它们与分数有什么相同点和不同点?
可以发现,这些式子与分数一样都是 (即A÷B)的形式.
分数的分子A与分母B都是整数,而这些式子中的A,B都是整式,并且B中都含有字母.
二 探索交流 发现新知
一般地,如果A、B都表示两个整式,并且B中含有字母,那么式子 叫做分式.其中A叫做分式的分子,B为分式的分母.
(1)分式是不同于整式的另一类式子.
(2)分母中含有字母是分式的一大特点.
(3)分式比分数更具有一般性. 例如,分数 仅表示2÷3的商,而分式 既可以表示2÷3,又可以表示(-5)÷2,8÷(-9)等.
二 探索交流 发现新知
思考:分式与分数有何联系?
②分数是分式中的字母取某些值的结果,分式更具一般性.
整数
整数
整式
整式
(分母含有字母)
分数
分式
类比思想
特殊到一般思想
①
7
100
a+1
100
二 探索交流 发现新知
整数
分数
整式
分式
有理数
有理式
数、式通性
(2)既然分式是不同于整式的另一类式子,那么它们统称为什么呢?
数的扩充
式的扩充
二 探索交流 发现新知
例1.下列各式哪些是整式?哪些是分式?
整式
整式
分式
整式
分式
整式
分式
整式
是分式吗?
是分式吗?
整式
分式
【点睛】1.判断时,注意含有π的式子,π是常数. 2.式子中含有多项时,若其中有一项分母含有字母,则该式也为分式,如:
典例精析
我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,
即当B≠0时,分式 才有意义.
分式有意义的条件
二 探索交流 发现新知
例2.下列分式中的字母满足什么条件时分式有意义?
解:(1)要使分式 有意义,则分母3x≠0,即x≠0;
(2)要使分式 有意义,则分母x-1≠0,即x≠1;
(3)要使分式 有意义,则分母5-3b≠0,即b≠ ;
(4)要使分式 有意义,则分母x-y≠0,即x≠y.
典例精析
例3.已知分式 有意义,则x应满足的条件是 ( )
A.x≠1 B.x≠2
C.x≠1且x≠2 D.以上结果都不对
C
【点睛】分式有意义的条件是分母不为零.如果分母是几个因式乘积的
形式,则每个因式都不为零.
典例精析
1.下列分式中的字母满足什么条件时分式有意义?
针对练习
下列各式中,无论x取何值时,分式都有意义的( )
D
针对练习
分式 的值为零应满足什么条件?分式 的值为正(负)应满足什么条件?
根据除法的意义及法则很容易得到:
1.当A=0且B≠0时,分式 的值为零.
2. 分式 的值为正时,A,B同号.
3. 分式 的值为负时,A,B异号.
二 探索交流 发现新知
解:当分子等于零而分母不等于零时,分式的值为零.
的值为零.
∴当x = 1时分式
x+1≠0,
则 x2 - 1=0,
例4 当x为何值时,分式 的值为零
典例精析
2.当 时,分式 的值为零.
x=2
【分析】要使分式的值为零,只需分子为零且分母不为零,
∴
解得x=2.
3.若 的值为零,则x= .
【分析】分式的值等于零,应满足分子等于零,同时分母不为零,即
解得x=-3.
-3
针对练习
例5. 已知分式
(2) 当x为何值时,分式的值是负数
(1) 当x为何值时,分式的值为正数
典例精析
例6 分式 的值是整数,求整数x的值.
典例精析
4.若分式的值为正数,则x的取值范围为( )
A.x≥- B.x≤-C.x>-且x≠0 D.x<-
5.若分式的值是负数,则x的取值范围是( )
A.x> B.x> C.x< D.x<
C
B
针对练习
6.(1)当x为何值时,分式 的值为负数
7.(1)分式 的值是整数,求整数x的值
(2)分式 的值是整数,求整数x的值
(2)若 值为正数,则的取值范围是
针对练习
一般地,如果A、B都表示两个整式,并且B中含有字母,那么式子
叫做分式.其中A叫做分式的分子,B为分式的分母.
1.当B≠0时,分式 才有意义.
2.当A=0且B≠0时,分式 的值为零.
3. 分式 的值为正时,A,B同号.
4. 分式 的值为负时,A,B异号.
课堂小结
课堂小结
1.下列各式中,,,,,是分式的有( )
A.0个 B.1个 C.2个 D.3个
2.要使分式有意义,x的取值应满足( )
A.x≠2 B.x≠﹣3 C.x≠2且x≠﹣3 D.x≠2或x≠﹣3
3.不论x取何值时,下列分式总有意义的是( )
A. B. C. D.
C
B
D
针对练习
4.若分式 的值为零,则x的值为( )
A.3或 3 B.3 C. 3 D.9
5.已知,则的值是( )
A.-5 B.5 C.-4 D.4
6.若代数式 的值为0,则x=______;当b=______时,分式无意义.
C
B
-2
-4
针对练习
7.当x的值为___________时,分式的值为负.
8.已知,则______.
9.分式的值是整数,则正整数的值等于___________.
10.观察下列各式:,-,,-,……,则第10个式子为_________.
<1且≠0
2或3或5
针对练习
11.当x为何值时,分式有意义?
解:由题意得,x-1≠0,x+2≠0,
解得x≠1且x≠-2.
12.当为何值时,分式的值为零?
解:∵的值为零
∴且
解得:,
当x=2时,
当x=-2时,,故舍去
综上:x=2
针对练习
13.已知分式,当时,分式的值为0;当时,分式没有意义,求的值.
解:时,分式的值为0,
,
.
时,分式没有意义,
,
.
.
针对练习
14.观察下列各式:
第1个等式:.
第2个等式:.
第3个等式:.
……
根据你发现的规律解答下列问题:
(1)第4个等式为:____________.
(2)写出你猜想的第n个等式:__________________(用含n的等式表示)
针对练习
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
