2022-2023学年高二化学人教版(2019)选择性必修2-3.1 物质的聚集状态与晶体的常识 课件 (41张ppt)
文档属性
| 名称 | 2022-2023学年高二化学人教版(2019)选择性必修2-3.1 物质的聚集状态与晶体的常识 课件 (41张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2022-12-06 10:10:17 | ||
图片预览










文档简介
(共41张PPT)
第一节 物质的聚集状态与晶体的常识
第一课时
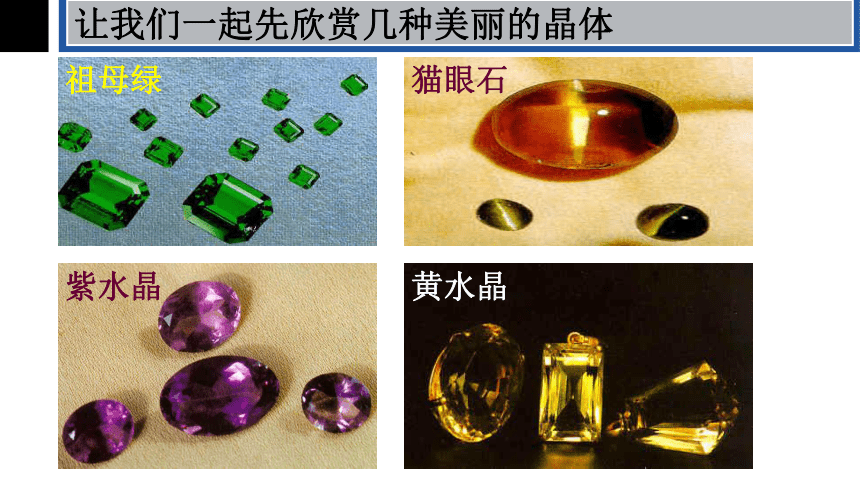
让我们一起先欣赏几种美丽的晶体
金刚石
胆矾
单质硫
雪花
食糖晶体
重
晶
石
让我们一起先欣赏几种美丽的晶体
祖母绿
猫眼石
紫水晶
黄水晶
晶体SiO2和非晶体SiO2的投影示意图
水晶
硅藻土
原子呈周期性有序排列
原子排列相对无序
内部微粒(原子、离子或分子)在空间按一定规律做周期性重复排列构成的固体物质称为晶体
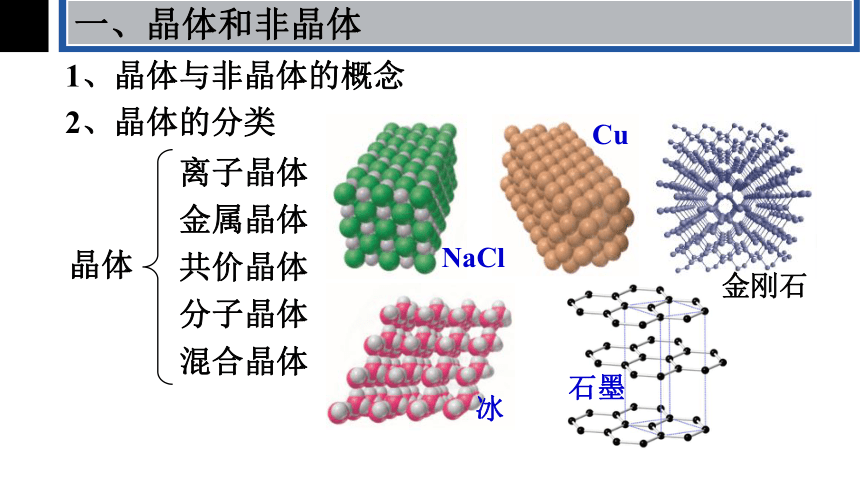
一、晶体和非晶体
1、晶体与非晶体的概念
晶体:
内部微粒(原子、离子或分子)在空间按一定
规律做周期性重复排列构成的固体物质
非晶体:
如橡胶、玻璃等固体,其内部原子或分子
的排列呈现相对无序的分布状态
(又称玻璃体)
Cu
NaCl
冰
一、晶体和非晶体
1、晶体与非晶体的概念
2、晶体的分类
晶体
离子晶体
金属晶体
共价晶体
分子晶体
混合晶体
Cu
NaCl
冰
石墨
金刚石
一、晶体和非晶体
3、晶体的特征与性质
微粒(原子、离子或分子)形成晶体是为了使整个体系能量达到最低的结果。微粒有序的按照一定的周期排列,每个微粒所处的化学环境与物理环境均相同,这样晶体中任意一个微粒都处于受力的平衡状态,是最稳定的状态。
因此晶体在微观层面上的特征就是长程有序(周期性);在宏观层面上的特征就是具有自发形成一定具有对称多面体外观的自范性。
一、晶体和非晶体
3、晶体的特征与性质
微观: 晶体粒子周期性有序排列,能量最低
能自发地呈现多面体外形的性质
(宏观体现)
(1)自范性:
晶体自范性的条件之一:晶体的生长速率适当
(本质特征)
外部正是由于降温速度过快而形成玛瑙,
内部冷却缓慢才形成具有规则多面体的水晶
天然水晶球
玛瑙
水晶
一、晶体和非晶体
3、晶体的特征与性质
微观: 晶体粒子周期性有序排列,能量最低
能自发地呈现多面体外形的性质
(宏观体现)
(1)自范性:
晶体自范性的条件之一:晶体的生长速率适当
(本质特征)
思考:得到晶体的途径,除了冷却的方法,还有没有其它途径?你能列举哪些?
探究实验 —— 获得晶体的途径
实验1、硫晶体的结晶
取少量硫粉置于蒸发皿中,加热至熔融态,停止加热,观察硫晶体的析出
实验2、碘的凝华
在一小烧杯中加入少量碘,用一个表面皿盖在小烧杯上,并在表面皿上加少量冷水。把小烧杯放在石棉网上 加热,观察实验现象
实验3、硫酸铜晶体的析出
取硫酸铜粉末配制高温饱和溶液,冷却析晶
一、晶体和非晶体
获得晶体的三个途径:(P61)
(1) 熔融态物质凝固
(2) 气态物质冷却不经过液态直接凝固(凝华)
(3) 溶质从溶液中析出
凝华得到的碘
从硫酸铜饱和溶液中析出的硫酸铜晶体
从熔融态结晶出来的硫晶体
晶体的特征与性质 —— 体验之旅
方解石CaCO3
(晶体)
玻璃片
(非晶体)
体验之旅一(光学性质):在白纸上划一条横线,分别透过玻璃片和方解石观察这条横线
结论:晶体光学性质的各向异性
各向异性:晶体在不同的方向上表现出不同的物理性质
晶体的特征与性质 —— 体验之旅
方解石CaCO3
(晶体)
玻璃片
(非晶体)
体验之旅二(硬度) :沿垂直方向在玻璃片和方解石表面刻划
方解石:感受到不同方向上的硬度不同,还会发现刻痕的深浅不一样
结论:晶体硬度的各向异性
晶体的特征与性质 —— 体验之旅
方解石CaCO3
(晶体)
玻璃片
(非晶体)
体验之旅三(机械强度):用锤子敲碎玻璃和方解石,又会产生什么奇怪的现象呢?
预测:方解石无限敲击会如何?
方解石的碎片形状相同
结论:晶体机械强度的各向异性
晶体的特征与性质 —— 体验之旅
体验之旅四:在水晶柱面上滴一滴融化的石蜡,用一根红热的铁针刺中凝固的石蜡。
现象:不同方向石蜡融化的快慢不同
结论:晶体导热性的各向异性
一、晶体和非晶体
3、晶体的特征与性质
能自发地呈现多面体外形的性质
(1)自范性:
(2)各向异性:
反映了晶体内部质点排列的有序性
强度、导热性、光学性质等
(3)固定的熔点 (非晶体无固定的熔点)
晶体具有周期性结构,各部分都按同一方式排列,热振动破坏晶格导致晶体融化时,各部分需要相同的温度;非晶体加热时则是逐步软化为流体,没有明确的熔点。
请同学们判断下列物质是晶体还是非晶体?
食盐
明矾
水晶
玛瑙
玻璃砖
石
蜡
思考:(1)能否通过是否有规则几何外形的固体来判断?
(2)粉末状的固体都是非晶体呢?
请同学们判断下列物质是晶体还是非晶体?
事实: 许多固体粉末用肉眼看不到晶体外形,但在光学显微镜下或电子显微镜下可观察到规则的晶体外形
那么怎样判断固体是晶体还是非晶体呢?
K2Cr2O7晶体 KNO3晶体 奈晶体
靠谱的方法:
X—射线衍射实验
一、晶体和非晶体
4、晶体的鉴别:X—射线衍射实验
晶体的周期性结构使它成为天然的三维光栅,周期与X-射线的波长相当,因此能够对X-射线产生衍射
晶体:分立的斑点
粉末:明锐的峰
学以致用 —— 鉴别假宝石
根据晶体的物理性质的各向异性的特点,人们很容易识别用玻璃仿造的假宝石。你能列举一些可能有效的方法鉴别假宝石吗?
①X—射线衍射
②观察宝石的外形,是否具有多面体的外形
④加热,测其是否具有固定的熔点
③观察固体的物理性质是否表现出各向异性
小结:晶体和非晶体的区别
固体 外观 微观结构 自范性 各向异性 熔点
晶 体
非 晶 体
本质区别
鉴别
具有规则的几何外形
粒子在空间周期性有序排列
有
各向异性
固定
不具有规则的几何外形
粒子排列相对无序
无
各向同性
不固定
微观粒子在空间是否呈现周期性有序排列
最科学的方法:X—射线衍射实验
知识拓展 —— 准晶体
美丽化学 —— 晶体之美
第一节 物质的聚集状态与晶体的常识
第二课时
二、晶胞
1、晶胞:描述晶体结构的基本单元
铜晶体
晶体与晶胞的关系可用蜂巢与峰室的关系比喻,然而蜂巢是有形的,晶胞是无形的,是人为划定的。
蜂巢与蜂室
铜晶胞
二、晶胞 —— 金刚石
金刚石晶体结构
金刚石晶胞示意图
二、晶胞
思考与交流:(1)上述铜晶体、金刚石、CO2晶体、NaCl晶体的晶胞的空间构形呈什么形状?
(2)在上述晶体中,晶胞是如何排列的?晶胞之间是否存在空隙?
平行六面体
无隙并置
金刚石晶胞
CO2晶胞
NaCl晶胞
铜晶胞
Na+
Cl-
二、晶胞
无隙并置
二、晶胞
1、晶胞:描述晶体结构的基本单元
2、特征:
一般来说,晶胞通常是一个平行六面体
决定了一个晶胞的上、下、左、右、前、后都有
与之完全相同的晶胞与其无隙并置
无隙: 指相邻的晶胞之间共用顶角、共用棱、共用面
并置: 指从一个晶胞到另一个晶胞只需平移晶胞框架,无需任何转动
二、晶胞 —— 晶胞的划分
例1、铜晶体的一个晶胞中含有_____个铜原子
4
二、晶胞 —— 晶胞的划分
练1、某晶胞的结构如图所示,这种晶体中A、B、C三种粒子数之比是( )
A. 3:9:4 B. 1:4:2 C. 2:9:4 D. 3:8:4
B
解析:
A = 6 × 1/12 = 1/2
B = 3 × 1/6 + 6 × 1/4 = 2
C = 1 × 1 = 1
2、晶胞中原子个数的计算 —— 均摊法
二、晶胞——晶胞中原子个数的计算(均摊法)
均摊法:如某个粒子为x个晶胞所共有,则该粒子有1/x属于一个晶胞。
顶点
面心
棱边
体心
2、晶胞中原子个数的计算 —— 均摊法
二、晶胞——晶胞中原子个数的计算(均摊法)
晶胞中粒子个数计算规律
晶胞 顶点 棱边 面心 体心
立方体
三棱柱
六棱柱
1/8
1/4
1/2
1
1/2
1
1/2
1
二、晶胞——晶胞中原子个数的计算(均摊法)
晶胞中粒子个数计算规律
晶胞 顶点 棱边 面心 体心
立方体 1/8 1/4 1/2 1
三棱柱 1/2 1
六棱柱 1/2 1
1/12
水平1/4 竖1/6
1/6
水平1/4 竖1/3
练2、石墨晶体的层状结构,层内为平面正六边形结构(如图),图中平均每个正六边形占有C原子数为____个、占有的碳碳键数为____个。碳原子数目与碳碳化学键数目之比为_____。
2 : 3
2
3
二、晶胞——晶胞中原子个数的计算(均摊法)
拓展:晶体的密度计算
Na+
Cl-
例2、(1)每个晶胞中平均有____个Na+,____个个Cl-;
(2)在NaCl晶体中,每个Na+周围最近距离的Cl-有___个;每个Cl-周围最近距离的Na+有___个。
(3)在NaCl晶体中,每个Na+周围最近距离的Na+有____个。
(4)该晶胞中,若两个距离最近的Na+核间距为a cm,
则晶体的密度ρ = _______ g·cm-3。
4
4
6
6
12
拓展:晶体的密度计算
ρ = =
Z · M
abc · NA
Z · M
V · NA
晶体的密度
ρ:晶体的密度(一般是g·cm-3)
Z:1个晶胞中化学式数目
M:化学式的摩尔质量(g·mol-1)
V: 1个晶胞的体积(一般是cm3)
NA:阿伏伽德罗常数(mol-1)
abc:晶胞参数(一般是pm或nm)
单位换算: 1m=102cm=109nm=1010 =1012pm
拓展:晶体的密度计算
Na+
Cl-
(4)该晶胞中,若两个距离最近的Na+核间距为a cm, 则晶体的密度ρ = _______ g·cm-3。
ρ = =
Z · M
abc · NA
Z · M
V · NA
acm
晶胞的边长:
晶胞的体积:
ρ = =
Z · M
abc · NA
4×58·5
2√2 a3 ×NA
√2 a cm
2√2 a3 cm3
=
58·5√2
a3 · NA
g·cm-3
拓展:晶体的密度计算
(2018年全国Ⅲ卷)金属Zn晶体中的原子堆积方式如图,六棱柱底边边长为a cm,高为c cm,阿伏伽德罗常数的值为NA,Zn的密度为_______g·cm-3(列出计算式)。
ρ =
Z · M
abc · NA
6×65
6× ×a2c×NA
3
4
√
=
拓展:晶体的密度计算
练4、下图是超导化合物一钙钛矿晶体中晶胞的结构。请回答:(1)该化合物的化学式为_______。
(2)在该化合物晶体中,与某个钛离子距离最近且相等的其他钛离子共有____个。
(3)设该化合物的相对分子质量为M,
密度为a g/cm3,阿伏加德罗常数为
NA,则晶体中钙离子与钛离子之间
的最短距离为__________。
CaTiO3
6
Ca O Ti
拓展:晶体的密度计算
(3)设该化合物的相对分子质量为M,密度为a g/cm3,阿伏加德罗常数为NA,则晶体中钙离子与钛离子之间的最短距离为__________。
Ca O Ti
d
√2 d
√3 d
第一节 物质的聚集状态与晶体的常识
第一课时
让我们一起先欣赏几种美丽的晶体
金刚石
胆矾
单质硫
雪花
食糖晶体
重
晶
石
让我们一起先欣赏几种美丽的晶体
祖母绿
猫眼石
紫水晶
黄水晶
晶体SiO2和非晶体SiO2的投影示意图
水晶
硅藻土
原子呈周期性有序排列
原子排列相对无序
内部微粒(原子、离子或分子)在空间按一定规律做周期性重复排列构成的固体物质称为晶体
一、晶体和非晶体
1、晶体与非晶体的概念
晶体:
内部微粒(原子、离子或分子)在空间按一定
规律做周期性重复排列构成的固体物质
非晶体:
如橡胶、玻璃等固体,其内部原子或分子
的排列呈现相对无序的分布状态
(又称玻璃体)
Cu
NaCl
冰
一、晶体和非晶体
1、晶体与非晶体的概念
2、晶体的分类
晶体
离子晶体
金属晶体
共价晶体
分子晶体
混合晶体
Cu
NaCl
冰
石墨
金刚石
一、晶体和非晶体
3、晶体的特征与性质
微粒(原子、离子或分子)形成晶体是为了使整个体系能量达到最低的结果。微粒有序的按照一定的周期排列,每个微粒所处的化学环境与物理环境均相同,这样晶体中任意一个微粒都处于受力的平衡状态,是最稳定的状态。
因此晶体在微观层面上的特征就是长程有序(周期性);在宏观层面上的特征就是具有自发形成一定具有对称多面体外观的自范性。
一、晶体和非晶体
3、晶体的特征与性质
微观: 晶体粒子周期性有序排列,能量最低
能自发地呈现多面体外形的性质
(宏观体现)
(1)自范性:
晶体自范性的条件之一:晶体的生长速率适当
(本质特征)
外部正是由于降温速度过快而形成玛瑙,
内部冷却缓慢才形成具有规则多面体的水晶
天然水晶球
玛瑙
水晶
一、晶体和非晶体
3、晶体的特征与性质
微观: 晶体粒子周期性有序排列,能量最低
能自发地呈现多面体外形的性质
(宏观体现)
(1)自范性:
晶体自范性的条件之一:晶体的生长速率适当
(本质特征)
思考:得到晶体的途径,除了冷却的方法,还有没有其它途径?你能列举哪些?
探究实验 —— 获得晶体的途径
实验1、硫晶体的结晶
取少量硫粉置于蒸发皿中,加热至熔融态,停止加热,观察硫晶体的析出
实验2、碘的凝华
在一小烧杯中加入少量碘,用一个表面皿盖在小烧杯上,并在表面皿上加少量冷水。把小烧杯放在石棉网上 加热,观察实验现象
实验3、硫酸铜晶体的析出
取硫酸铜粉末配制高温饱和溶液,冷却析晶
一、晶体和非晶体
获得晶体的三个途径:(P61)
(1) 熔融态物质凝固
(2) 气态物质冷却不经过液态直接凝固(凝华)
(3) 溶质从溶液中析出
凝华得到的碘
从硫酸铜饱和溶液中析出的硫酸铜晶体
从熔融态结晶出来的硫晶体
晶体的特征与性质 —— 体验之旅
方解石CaCO3
(晶体)
玻璃片
(非晶体)
体验之旅一(光学性质):在白纸上划一条横线,分别透过玻璃片和方解石观察这条横线
结论:晶体光学性质的各向异性
各向异性:晶体在不同的方向上表现出不同的物理性质
晶体的特征与性质 —— 体验之旅
方解石CaCO3
(晶体)
玻璃片
(非晶体)
体验之旅二(硬度) :沿垂直方向在玻璃片和方解石表面刻划
方解石:感受到不同方向上的硬度不同,还会发现刻痕的深浅不一样
结论:晶体硬度的各向异性
晶体的特征与性质 —— 体验之旅
方解石CaCO3
(晶体)
玻璃片
(非晶体)
体验之旅三(机械强度):用锤子敲碎玻璃和方解石,又会产生什么奇怪的现象呢?
预测:方解石无限敲击会如何?
方解石的碎片形状相同
结论:晶体机械强度的各向异性
晶体的特征与性质 —— 体验之旅
体验之旅四:在水晶柱面上滴一滴融化的石蜡,用一根红热的铁针刺中凝固的石蜡。
现象:不同方向石蜡融化的快慢不同
结论:晶体导热性的各向异性
一、晶体和非晶体
3、晶体的特征与性质
能自发地呈现多面体外形的性质
(1)自范性:
(2)各向异性:
反映了晶体内部质点排列的有序性
强度、导热性、光学性质等
(3)固定的熔点 (非晶体无固定的熔点)
晶体具有周期性结构,各部分都按同一方式排列,热振动破坏晶格导致晶体融化时,各部分需要相同的温度;非晶体加热时则是逐步软化为流体,没有明确的熔点。
请同学们判断下列物质是晶体还是非晶体?
食盐
明矾
水晶
玛瑙
玻璃砖
石
蜡
思考:(1)能否通过是否有规则几何外形的固体来判断?
(2)粉末状的固体都是非晶体呢?
请同学们判断下列物质是晶体还是非晶体?
事实: 许多固体粉末用肉眼看不到晶体外形,但在光学显微镜下或电子显微镜下可观察到规则的晶体外形
那么怎样判断固体是晶体还是非晶体呢?
K2Cr2O7晶体 KNO3晶体 奈晶体
靠谱的方法:
X—射线衍射实验
一、晶体和非晶体
4、晶体的鉴别:X—射线衍射实验
晶体的周期性结构使它成为天然的三维光栅,周期与X-射线的波长相当,因此能够对X-射线产生衍射
晶体:分立的斑点
粉末:明锐的峰
学以致用 —— 鉴别假宝石
根据晶体的物理性质的各向异性的特点,人们很容易识别用玻璃仿造的假宝石。你能列举一些可能有效的方法鉴别假宝石吗?
①X—射线衍射
②观察宝石的外形,是否具有多面体的外形
④加热,测其是否具有固定的熔点
③观察固体的物理性质是否表现出各向异性
小结:晶体和非晶体的区别
固体 外观 微观结构 自范性 各向异性 熔点
晶 体
非 晶 体
本质区别
鉴别
具有规则的几何外形
粒子在空间周期性有序排列
有
各向异性
固定
不具有规则的几何外形
粒子排列相对无序
无
各向同性
不固定
微观粒子在空间是否呈现周期性有序排列
最科学的方法:X—射线衍射实验
知识拓展 —— 准晶体
美丽化学 —— 晶体之美
第一节 物质的聚集状态与晶体的常识
第二课时
二、晶胞
1、晶胞:描述晶体结构的基本单元
铜晶体
晶体与晶胞的关系可用蜂巢与峰室的关系比喻,然而蜂巢是有形的,晶胞是无形的,是人为划定的。
蜂巢与蜂室
铜晶胞
二、晶胞 —— 金刚石
金刚石晶体结构
金刚石晶胞示意图
二、晶胞
思考与交流:(1)上述铜晶体、金刚石、CO2晶体、NaCl晶体的晶胞的空间构形呈什么形状?
(2)在上述晶体中,晶胞是如何排列的?晶胞之间是否存在空隙?
平行六面体
无隙并置
金刚石晶胞
CO2晶胞
NaCl晶胞
铜晶胞
Na+
Cl-
二、晶胞
无隙并置
二、晶胞
1、晶胞:描述晶体结构的基本单元
2、特征:
一般来说,晶胞通常是一个平行六面体
决定了一个晶胞的上、下、左、右、前、后都有
与之完全相同的晶胞与其无隙并置
无隙: 指相邻的晶胞之间共用顶角、共用棱、共用面
并置: 指从一个晶胞到另一个晶胞只需平移晶胞框架,无需任何转动
二、晶胞 —— 晶胞的划分
例1、铜晶体的一个晶胞中含有_____个铜原子
4
二、晶胞 —— 晶胞的划分
练1、某晶胞的结构如图所示,这种晶体中A、B、C三种粒子数之比是( )
A. 3:9:4 B. 1:4:2 C. 2:9:4 D. 3:8:4
B
解析:
A = 6 × 1/12 = 1/2
B = 3 × 1/6 + 6 × 1/4 = 2
C = 1 × 1 = 1
2、晶胞中原子个数的计算 —— 均摊法
二、晶胞——晶胞中原子个数的计算(均摊法)
均摊法:如某个粒子为x个晶胞所共有,则该粒子有1/x属于一个晶胞。
顶点
面心
棱边
体心
2、晶胞中原子个数的计算 —— 均摊法
二、晶胞——晶胞中原子个数的计算(均摊法)
晶胞中粒子个数计算规律
晶胞 顶点 棱边 面心 体心
立方体
三棱柱
六棱柱
1/8
1/4
1/2
1
1/2
1
1/2
1
二、晶胞——晶胞中原子个数的计算(均摊法)
晶胞中粒子个数计算规律
晶胞 顶点 棱边 面心 体心
立方体 1/8 1/4 1/2 1
三棱柱 1/2 1
六棱柱 1/2 1
1/12
水平1/4 竖1/6
1/6
水平1/4 竖1/3
练2、石墨晶体的层状结构,层内为平面正六边形结构(如图),图中平均每个正六边形占有C原子数为____个、占有的碳碳键数为____个。碳原子数目与碳碳化学键数目之比为_____。
2 : 3
2
3
二、晶胞——晶胞中原子个数的计算(均摊法)
拓展:晶体的密度计算
Na+
Cl-
例2、(1)每个晶胞中平均有____个Na+,____个个Cl-;
(2)在NaCl晶体中,每个Na+周围最近距离的Cl-有___个;每个Cl-周围最近距离的Na+有___个。
(3)在NaCl晶体中,每个Na+周围最近距离的Na+有____个。
(4)该晶胞中,若两个距离最近的Na+核间距为a cm,
则晶体的密度ρ = _______ g·cm-3。
4
4
6
6
12
拓展:晶体的密度计算
ρ = =
Z · M
abc · NA
Z · M
V · NA
晶体的密度
ρ:晶体的密度(一般是g·cm-3)
Z:1个晶胞中化学式数目
M:化学式的摩尔质量(g·mol-1)
V: 1个晶胞的体积(一般是cm3)
NA:阿伏伽德罗常数(mol-1)
abc:晶胞参数(一般是pm或nm)
单位换算: 1m=102cm=109nm=1010 =1012pm
拓展:晶体的密度计算
Na+
Cl-
(4)该晶胞中,若两个距离最近的Na+核间距为a cm, 则晶体的密度ρ = _______ g·cm-3。
ρ = =
Z · M
abc · NA
Z · M
V · NA
acm
晶胞的边长:
晶胞的体积:
ρ = =
Z · M
abc · NA
4×58·5
2√2 a3 ×NA
√2 a cm
2√2 a3 cm3
=
58·5√2
a3 · NA
g·cm-3
拓展:晶体的密度计算
(2018年全国Ⅲ卷)金属Zn晶体中的原子堆积方式如图,六棱柱底边边长为a cm,高为c cm,阿伏伽德罗常数的值为NA,Zn的密度为_______g·cm-3(列出计算式)。
ρ =
Z · M
abc · NA
6×65
6× ×a2c×NA
3
4
√
=
拓展:晶体的密度计算
练4、下图是超导化合物一钙钛矿晶体中晶胞的结构。请回答:(1)该化合物的化学式为_______。
(2)在该化合物晶体中,与某个钛离子距离最近且相等的其他钛离子共有____个。
(3)设该化合物的相对分子质量为M,
密度为a g/cm3,阿伏加德罗常数为
NA,则晶体中钙离子与钛离子之间
的最短距离为__________。
CaTiO3
6
Ca O Ti
拓展:晶体的密度计算
(3)设该化合物的相对分子质量为M,密度为a g/cm3,阿伏加德罗常数为NA,则晶体中钙离子与钛离子之间的最短距离为__________。
Ca O Ti
d
√2 d
√3 d
