2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和(第一课时)课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和(第一课时)课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 19:34:12 | ||
图片预览






文档简介
(共22张PPT)
4.2.2 等差数列的前n项和
(第一课时)
高斯出生于一个工匠家庭,幼时家境贫困,但聪敏异常。上小学四年级时,一次老师布置了一道数学习题:“把从1到100的自然数加起来,和是多少?”年仅10岁的小高斯略一思索就得到答案5050,这使老师非常吃惊。那么高斯是采用了什么方法来巧妙地计算出来的呢?
高斯(1777---1855), 德国数学家、物理学家和天文学家。他和牛顿、阿基米德,被誉为有史以来的三大数学家。有“数学王子”之称。
高斯“神速求和”的故事:
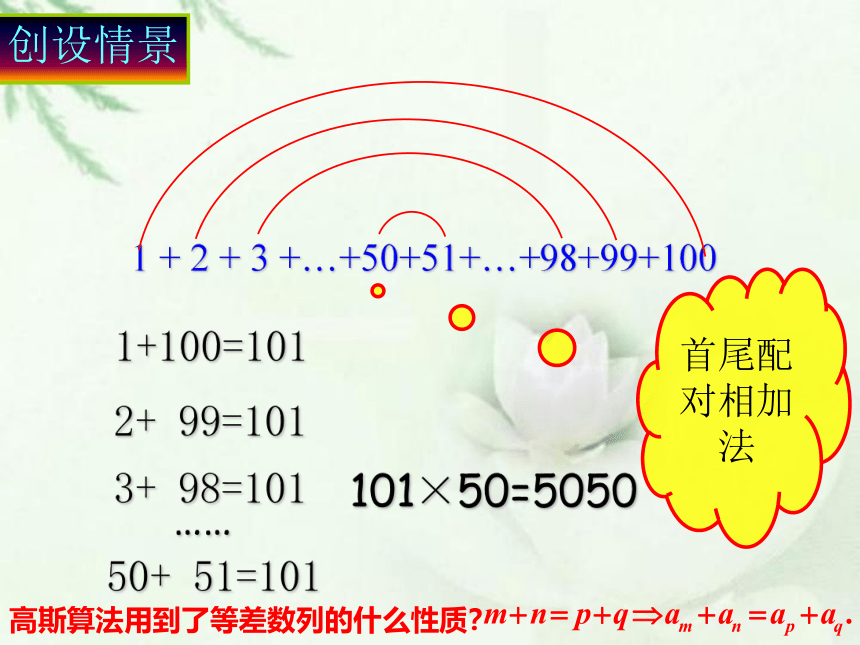
创设情景
1 + 2 + 3 +…+50+51+…+98+99+100
1+100=101
2+ 99=101
3+ 98=101
……
50+ 51=101
101×50=5050
首尾配对相加法
创设情景
高斯算法用到了等差数列的什么性质?
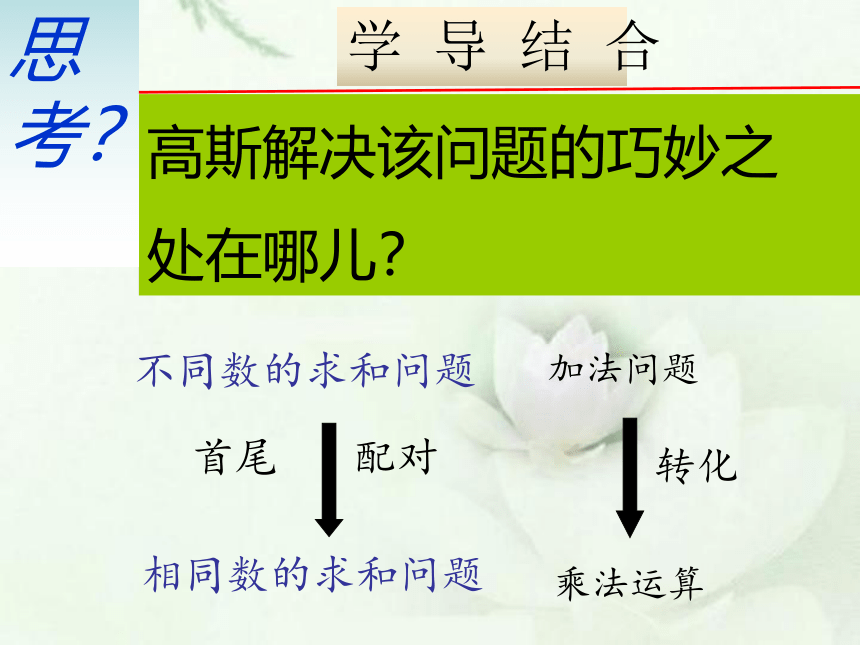
不同数的求和问题
相同数的求和问题
首尾
配对
高斯解决该问题的巧妙之
处在哪儿?
思考?
学 导 结 合
乘法运算
加法问题
转化
科技是国家强盛之基,创新是民族进步之魂
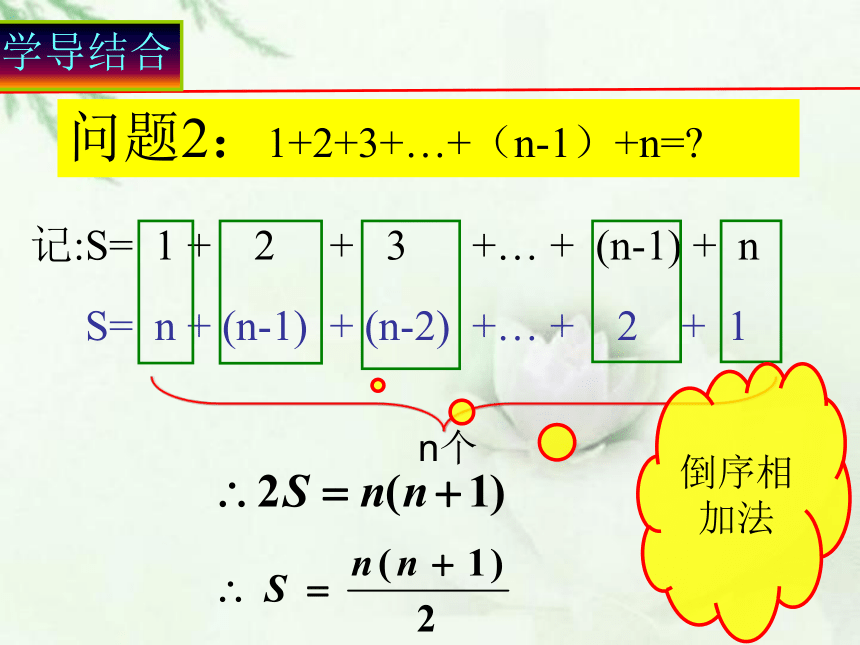
问题2:1+2+3+…+(n-1)+n=
记:S= 1 + 2 + 3 +… + (n-1) + n
S= n + (n-1) + (n-2) +… + 2 + 1
n个
学导结合
倒序相加法
讲授新课
数列{an}的前n项和定义:
一般地,我们称
a1+a2+a3+…+an
为数列{an}的前n项和,用Sn表示,
即 Sn= a1+a2+a3+…+an
Sn= a1 + a2 + a3 +…+ an-1 + an
Sn= an + an-1 + an-2 + … + a2 + a1
对于等差数列 ,我们用两种方式表示
n个
探究新知
等差数列的前n项和公式
公式1
公式2
知
三
求
二
得出新知
n
a1
an
用几何法理解等差数列的前n项和公式
识记新知
我们可结合梯形的面积公式来理解记忆
等差数列前 n 项和公式.
a1
(n-1)d
n
a1
an
将梯形分割成一个平行四边形和一个三角形.
识记新知
分析:
(1)可以直接利用公式求和;
(2)可以先利用的值求出d,再利用公式求和;
应用新知
合作探究
解:
所以
得
整理,得
解得 n=12,或n=-5(舍去)
所以 n=12
解:
练习
思考:上述四道题分别选择哪种公式更方便计算
公式1
公式2
(1) 5+6+7+…+79+80
(2) 1+3+5+…+(2n-1)
思考:如何求下列数列的和?
应用新知
思考1:上述两个式子是什么数列的和?
思考2:从给定的式子中能读取数列的a1,d,n,an中的哪几种数值?
(1)a1=5,d=1,an=80 (2)a1=1,d=2,an=2n-1
思考3:选择哪种求和公式更方便计算?
解:(1)∵数列5,6,7……79,80是等差数列,
可设为{an}且a1=5,d=1,an=80
∴5+(n-1)=80
∴n=76(也可根据数列特征求出80-4=76)
∴S76=3230,∴5+6+7+…+79+80=3230
等差数列
(1) 5+6+7+…+79+80
(2) 1+3+5+…+(2n-1)
思考:如何求下列数列的和?
应用新知
思考1:上述两个式子是什么数列的和?
思考2:从给定的式子中能读取数列的a1,d,n,an中的哪几种数值?
(1)a1=5,d=1,an=80 (2)a1=1,d=2,an=2n-1
思考3:选择哪种求和公式更方便计算?
解:(2)∵数列1,3,5……2n-1是等差数列,
可设为{an}且a1=1,d=2,an=2n-1 项数:n
∴Sn=n2,∴1+3+5+…+(2n-1)=n2
等差数列
练习
解:设等差数列-1,-3,-5为{an},公差为d,
则a1=-1,d=-2,Sn=-100
将上述数值代入
可得n=10
例7、已知等差数列{an}的前10项和是310,前20项和是1220,求等差数列{an}的前n项和Sn.
探究深化
激情展示 我最棒
在等差数列 {an} 中,如果已知五个元素 a1, an, n, d, Sn 中的任意三个, 可以求出其余两个量 .
解题思路一般是:建立方程(组)求解
解:
由题意,知
把它们代入公式
得
解方程组,得
代入
例7、已知等差数列{an}的前10项和是310,前20项和是1220,求等差数列{an}的前n项和Sn.
=3n2+n
练习
一个方法
两个公式
倒序相加法
总结反思
数形结合思想 、转化思想 、 方程思想(知三求二)
三个思想
4.2.2 等差数列的前n项和
(第一课时)
高斯出生于一个工匠家庭,幼时家境贫困,但聪敏异常。上小学四年级时,一次老师布置了一道数学习题:“把从1到100的自然数加起来,和是多少?”年仅10岁的小高斯略一思索就得到答案5050,这使老师非常吃惊。那么高斯是采用了什么方法来巧妙地计算出来的呢?
高斯(1777---1855), 德国数学家、物理学家和天文学家。他和牛顿、阿基米德,被誉为有史以来的三大数学家。有“数学王子”之称。
高斯“神速求和”的故事:
创设情景
1 + 2 + 3 +…+50+51+…+98+99+100
1+100=101
2+ 99=101
3+ 98=101
……
50+ 51=101
101×50=5050
首尾配对相加法
创设情景
高斯算法用到了等差数列的什么性质?
不同数的求和问题
相同数的求和问题
首尾
配对
高斯解决该问题的巧妙之
处在哪儿?
思考?
学 导 结 合
乘法运算
加法问题
转化
科技是国家强盛之基,创新是民族进步之魂
问题2:1+2+3+…+(n-1)+n=
记:S= 1 + 2 + 3 +… + (n-1) + n
S= n + (n-1) + (n-2) +… + 2 + 1
n个
学导结合
倒序相加法
讲授新课
数列{an}的前n项和定义:
一般地,我们称
a1+a2+a3+…+an
为数列{an}的前n项和,用Sn表示,
即 Sn= a1+a2+a3+…+an
Sn= a1 + a2 + a3 +…+ an-1 + an
Sn= an + an-1 + an-2 + … + a2 + a1
对于等差数列 ,我们用两种方式表示
n个
探究新知
等差数列的前n项和公式
公式1
公式2
知
三
求
二
得出新知
n
a1
an
用几何法理解等差数列的前n项和公式
识记新知
我们可结合梯形的面积公式来理解记忆
等差数列前 n 项和公式.
a1
(n-1)d
n
a1
an
将梯形分割成一个平行四边形和一个三角形.
识记新知
分析:
(1)可以直接利用公式求和;
(2)可以先利用的值求出d,再利用公式求和;
应用新知
合作探究
解:
所以
得
整理,得
解得 n=12,或n=-5(舍去)
所以 n=12
解:
练习
思考:上述四道题分别选择哪种公式更方便计算
公式1
公式2
(1) 5+6+7+…+79+80
(2) 1+3+5+…+(2n-1)
思考:如何求下列数列的和?
应用新知
思考1:上述两个式子是什么数列的和?
思考2:从给定的式子中能读取数列的a1,d,n,an中的哪几种数值?
(1)a1=5,d=1,an=80 (2)a1=1,d=2,an=2n-1
思考3:选择哪种求和公式更方便计算?
解:(1)∵数列5,6,7……79,80是等差数列,
可设为{an}且a1=5,d=1,an=80
∴5+(n-1)=80
∴n=76(也可根据数列特征求出80-4=76)
∴S76=3230,∴5+6+7+…+79+80=3230
等差数列
(1) 5+6+7+…+79+80
(2) 1+3+5+…+(2n-1)
思考:如何求下列数列的和?
应用新知
思考1:上述两个式子是什么数列的和?
思考2:从给定的式子中能读取数列的a1,d,n,an中的哪几种数值?
(1)a1=5,d=1,an=80 (2)a1=1,d=2,an=2n-1
思考3:选择哪种求和公式更方便计算?
解:(2)∵数列1,3,5……2n-1是等差数列,
可设为{an}且a1=1,d=2,an=2n-1 项数:n
∴Sn=n2,∴1+3+5+…+(2n-1)=n2
等差数列
练习
解:设等差数列-1,-3,-5为{an},公差为d,
则a1=-1,d=-2,Sn=-100
将上述数值代入
可得n=10
例7、已知等差数列{an}的前10项和是310,前20项和是1220,求等差数列{an}的前n项和Sn.
探究深化
激情展示 我最棒
在等差数列 {an} 中,如果已知五个元素 a1, an, n, d, Sn 中的任意三个, 可以求出其余两个量 .
解题思路一般是:建立方程(组)求解
解:
由题意,知
把它们代入公式
得
解方程组,得
代入
例7、已知等差数列{an}的前10项和是310,前20项和是1220,求等差数列{an}的前n项和Sn.
=3n2+n
练习
一个方法
两个公式
倒序相加法
总结反思
数形结合思想 、转化思想 、 方程思想(知三求二)
三个思想
