2022-2023学年高一上学期数学人教A版(2019)必修第一册5.4.1正弦函数、余弦函数的图象课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册5.4.1正弦函数、余弦函数的图象课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
正弦函数、余弦函数的图象
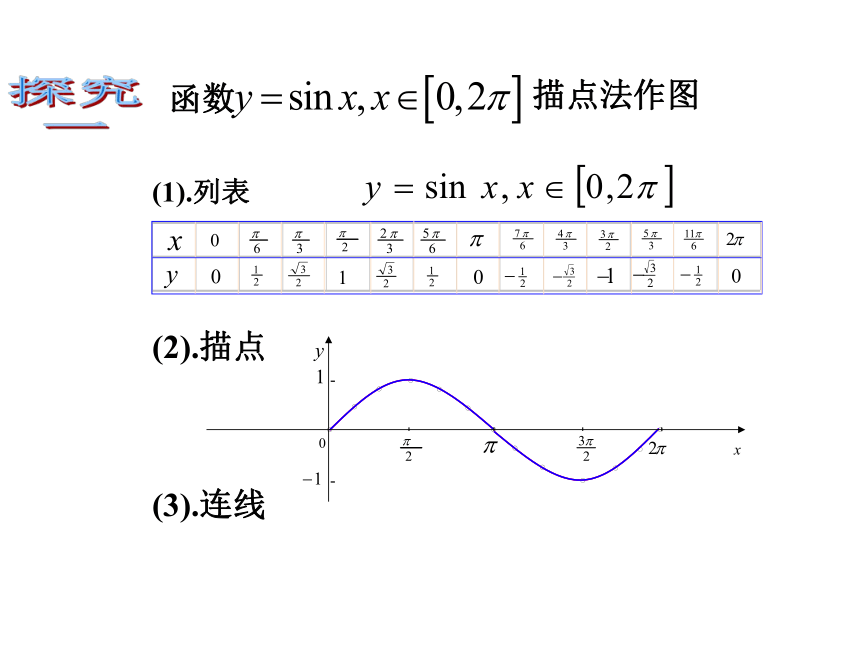
(1).列表
(2).描点
(3).连线
-
-
-
-
-
-
探究一
函数
描点法作图
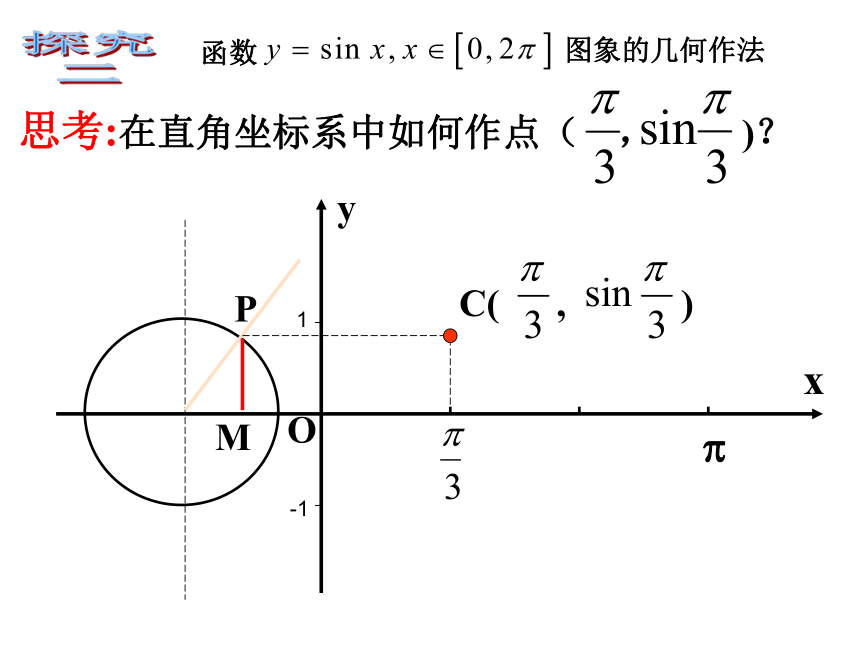
思考:在直角坐标系中如何作点( , )?
P
M
C( , )
y
x
O
1
-1
函数
图象的几何作法
探究二
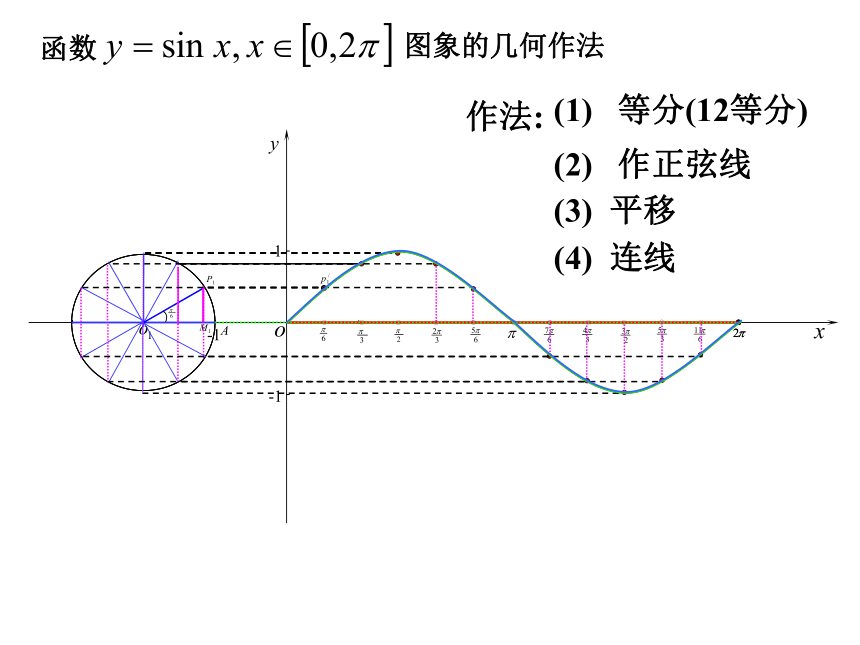
函数
图象的几何作法
-
-
-1
1
-
-
-1
-
-
作法:
(1) 等分(12等分)
(2) 作正弦线
(3) 平移
(4) 连线
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx x [0,2 ]
y=sinx x R
正弦曲线
y
x
o
1
-1
终边相同角的三角函数值相等
即: sin(x+2k )=sinx, k Z
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦、余弦函数的图象
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx=sin(x+ ), x R
余弦曲线
正弦曲线
形状完全一样只是位置不同
正弦、余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx x [0,2 ]
y=sinx x R
正弦曲线
y
x
o
1
-1
如何作出正弦函数的图象(在精确度要求不太高时)?
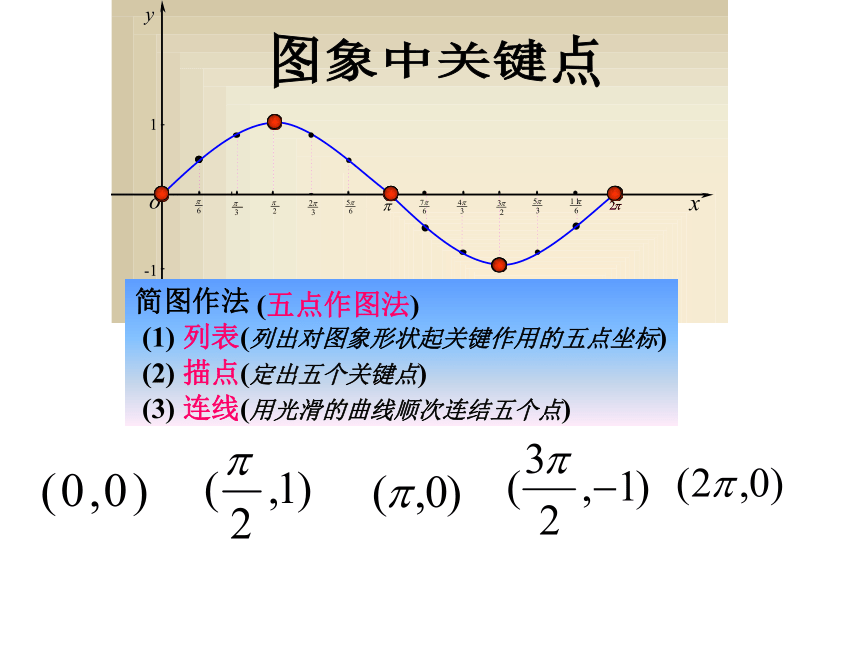
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
五点法画图
图象中关键点
简图作法
(五点作图法)
(1) 列表(列出对图象形状起关键作用的五点坐标)
(2) 描点(定出五个关键点)
(3) 连线(用光滑的曲线顺次连结五个点)
五点法
余弦函数 的五个关键点
物 理 小 实 验
1.单摆实验
2.弹簧振子
演示:沙漏实验
演示:弹簧振子
例1 画出下列函数的简图:
解:(1)按五个关键点列表:
(2)按五个关键点列表:
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
仔细观察正弦、余弦函数的图象,并思考以下几个问题:
(1)正弦、余弦函数的定义域是什么?
(2)正弦、余弦函数的值域是什么?
(3)它们的最值情况如何?
(4)它们的正负值区间如何分?
正弦曲线
余弦曲线
(1)正弦、余弦函数的定义域都是R。
(2)正弦、余弦函数的值域都是[-1,1]。
因为正弦线、余弦线的长度小于或等于单位圆的半径的长度,
所以 即
称为正弦、余弦函数的有界性。
余弦函数 ,当 时, ;
当 时,
-1
y
x
o
1
y=cosx,x [0, 2 ]
y
x
o
1
-1
y=sinx,x [0, 2 ]
正弦函数 , 当 时, ;
当 时, ;
(3)取最大值、最小值情况:
(4)正负值区间:
-1
y
x
o
1
y=cosx,x [0, 2 ]
y
x
o
1
-1
y=sinx,x [0, 2 ]
例1 求下列函数的定义域:
练习:
1、函数 的最大值和最小值分别为 ( )
A、2、-2 B、4、0
C、2、0 D、4、-4
答案:
B
2、求下列函数的定义域:
正弦函数、余弦函数的图象
(1).列表
(2).描点
(3).连线
-
-
-
-
-
-
探究一
函数
描点法作图
思考:在直角坐标系中如何作点( , )?
P
M
C( , )
y
x
O
1
-1
函数
图象的几何作法
探究二
函数
图象的几何作法
-
-
-1
1
-
-
-1
-
-
作法:
(1) 等分(12等分)
(2) 作正弦线
(3) 平移
(4) 连线
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx x [0,2 ]
y=sinx x R
正弦曲线
y
x
o
1
-1
终边相同角的三角函数值相等
即: sin(x+2k )=sinx, k Z
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦、余弦函数的图象
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx=sin(x+ ), x R
余弦曲线
正弦曲线
形状完全一样只是位置不同
正弦、余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx x [0,2 ]
y=sinx x R
正弦曲线
y
x
o
1
-1
如何作出正弦函数的图象(在精确度要求不太高时)?
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
五点法画图
图象中关键点
简图作法
(五点作图法)
(1) 列表(列出对图象形状起关键作用的五点坐标)
(2) 描点(定出五个关键点)
(3) 连线(用光滑的曲线顺次连结五个点)
五点法
余弦函数 的五个关键点
物 理 小 实 验
1.单摆实验
2.弹簧振子
演示:沙漏实验
演示:弹簧振子
例1 画出下列函数的简图:
解:(1)按五个关键点列表:
(2)按五个关键点列表:
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
仔细观察正弦、余弦函数的图象,并思考以下几个问题:
(1)正弦、余弦函数的定义域是什么?
(2)正弦、余弦函数的值域是什么?
(3)它们的最值情况如何?
(4)它们的正负值区间如何分?
正弦曲线
余弦曲线
(1)正弦、余弦函数的定义域都是R。
(2)正弦、余弦函数的值域都是[-1,1]。
因为正弦线、余弦线的长度小于或等于单位圆的半径的长度,
所以 即
称为正弦、余弦函数的有界性。
余弦函数 ,当 时, ;
当 时,
-1
y
x
o
1
y=cosx,x [0, 2 ]
y
x
o
1
-1
y=sinx,x [0, 2 ]
正弦函数 , 当 时, ;
当 时, ;
(3)取最大值、最小值情况:
(4)正负值区间:
-1
y
x
o
1
y=cosx,x [0, 2 ]
y
x
o
1
-1
y=sinx,x [0, 2 ]
例1 求下列函数的定义域:
练习:
1、函数 的最大值和最小值分别为 ( )
A、2、-2 B、4、0
C、2、0 D、4、-4
答案:
B
2、求下列函数的定义域:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
