5.2圆的周长易错题(试题)六年级上册数学人教版(带答案)
文档属性
| 名称 | 5.2圆的周长易错题(试题)六年级上册数学人教版(带答案) |  | |
| 格式 | docx | ||
| 文件大小 | 526.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 11:18:09 | ||
图片预览




文档简介
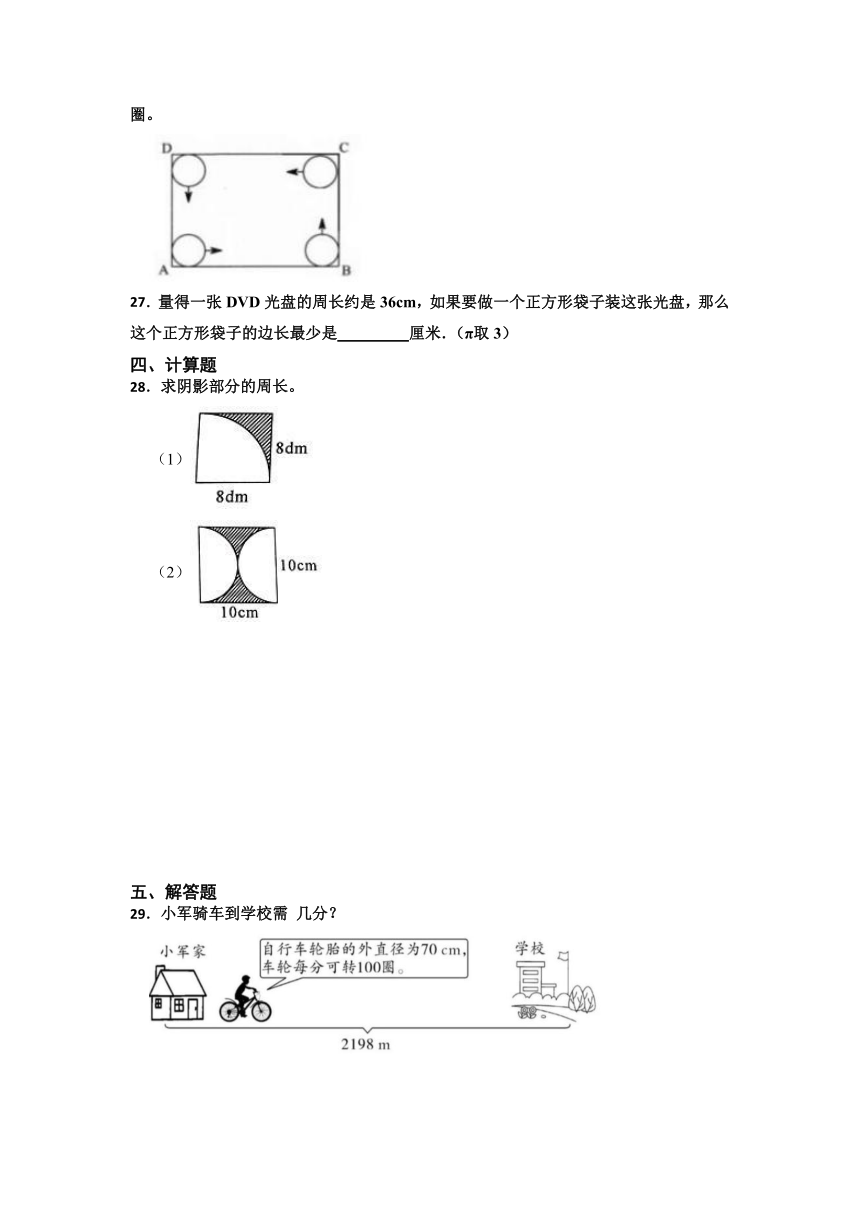
小学数学六年级上册《圆的周长》专题经典易错题(通用版)
一、单选题
1.下图中从M到N,走路①与路②的结果是( )。
A.路①远 B.路②远 C.一样远
2.自行车的前轮半径为30厘米,后轮半径为20厘米。如下图,当前轮向前行驶了5圈回到E点的位置时,后轮F点的位置是下图中的( )。
A. B. C. D.
3.如图,把一支铅笔垂直插入一个半径为1cm的圆形硬纸板的圆心,然后绕一个直径为8cm的量角器的圆弧滚动,铅笔会留下痕迹,此痕迹的长是( )cm。
A.12.56 B.20.7 C.15.7 D.28.26
4.一个半圆的周长是25.7cm,这个半圆的直径是( )。
A.2.57cm B.5cm C.10cm D.314cm
5.下列关于圆的说法正确的是( )。
A.半径确定圆的位置 B.圆是轴对称图形
C.圆周率是周长与半径的比值 D.圆的对称轴是直径
6.把一个周长是18.84分米的圆平均分成两个半圆,每个半圆的周长是( )分米。
A.15.42 B.9.42 C.12.24 D.12.56
7.如图,六位朋友均匀的围坐在圆桌旁聚会,圆桌的半径为110cm,每人离桌边10cm,则图中相邻两人之间的圆弧的长(结果保留π)为( )
A.10π cm B.20π cm C.30π cm D.40π cm
8.如图中有大、中、小三个圆,且中圆与小圆的直径之和等于大圆的直径,已知大圆周长比中圆周长长4π厘米,那么小圆半径是( )厘米.(π为圆周率)
A.4 B.3 C.2 D.1
9.把一个周长为12.56cm的圆剪成两个半圆形,每个半圆形的周长是( )cm。
A.12.56 B.6.28 C.10.28 D.25.12
10.如图,一台压路机的前轮直径是1.2米,如果前轮每分钟转6圈,压路机5分钟前进 米?
A.113.04 B.134.06 C.125.76 D.131.04
11.如下图,四个圆的圆心在一条直线上,大圆的周长与三个小圆的周长之和比较,结果是( )。
A.大圆的周长较长 B.大圆的周长较短
C.相等 D.无法比较
12.从A到B,蚂蚁甲沿①号路线爬行,蚂蚁乙沿②号路线爬,如果它们的速度相同,它们爬行用的时间比,( )。
A.甲用的时间多 B.一样 C.乙用的时间多
13.用一块长12米,宽7米的长方形铁皮剪半径是1.5米的圆,最多能剪( )个.
A.11 B.8 C.10 D.13
14.把一张圆形纸片沿半径平均分成若干份,拼成一个近似长方形,其周长( )。
A.等于圆周长 B.大于圆周长 C.小于圆周长 D.无法比较
15.一辆自行车的车轮半径是30厘米,这辆自行车通过一条1884米长的街道时,车轮要转大约( )周.
A.10 B.100 C.1000 D.2000
二、判断题
16.一个圆形挂钟分针长10cm,这根分针的尖端15分钟所走的路程是15.7cm。( )
17.一个圆的周长是9.42米,剪成两个半圆后每个半圆的周长是4.71米.( )
三、填空题
18.一个时钟的分针长10厘米,从8:00走到8:30,分针针尖走过了 厘米。
19.一个圆的半径扩大到原来的3倍后周长比原来多37.68厘米,原来圆的周长 厘米。
20.一个圆周长、直径、半径的和是27.84厘米,这个圆的半径是 厘米。
21.一个圆形花圃的直径是40米,李大爷每天早晨绕着花圃跑10圈,李大爷每天早晨大约跑 米?如果沿着这个花圃的边线大约每隔5米种一棵杜鹃,大约可种 棵?
22.在标准400m跑道上,参加200m跑,每条跑道宽1.25m,相邻跑道中两人之间的起跑位置大约相差 m。(π取3.14)
23.一辆自行车的车轮半径是30cm,这辆自行车通过一条1413m长的街道时,车轮要转 圈。
24.(如图)一个半圆形花坛的周长是51.4米,半径是 米。
25.一张长18cm、宽15cm的长方形纸,最多可以剪 个周长12.56cm的圆。
26.如图,在长、宽分别为14cm,8cm的方框中,用一个半径为1cm的圆形纸片,无滑动地沿着方框按A-B-C-D-A的方向滚动。(本题中π的值取3)若纸片贴着方框内侧滚动一周回到出发位置,则圆心运动轨迹的长度是 cm,圆形纸片共转动了 圈。
27.量得一张DVD光盘的周长约是36cm,如果要做一个正方形袋子装这张光盘,那么这个正方形袋子的边长最少是 厘米.(π取3)
四、计算题
28.求阴影部分的周长。
(1)
(2)
五、解答题
29.小军骑车到学校需 几分?
30.一辆电动自行车的车轮直径是0.6米,如果每分转180周,这辆电动车5分钟可行多少米?
31.如图,有一只狗被拴在一个建筑物的墙角点A处,这个建筑物的底面是一个边长为8 m的正方形,拴狗的绳长18m。现在狗从点B出发,将绳拉紧并沿顺时针方向跑。狗最多可以跑多少米?
32.大本钟——伦敦市的标志性建筑物.钟盘上时针的长度是2.75m。大本钟的时针经过6小时后,时针的尖端走过的路程是多少米?经过9小时呢?
33.自行车车轮的外直径约为0.75m,晓晓骑自行车通过一座长3768m的大桥,车轮每分钟转200周,通过这座大桥共需要多少分钟?
34.杂技演员表演独轮车走钢丝,车轮的直径是40cm。要骑过31.4m长的钢丝,车轮要转动多少圈?
35.如图,两个圆只有一个公共点C,大圆直径AC为50厘米,小圆直径BC为30厘米。甲、乙两只蚂蚁同时从C点出发,甲蚂蚁以每秒0.6厘米的速度顺时针沿着大圆圆周爬行,乙蚂蚁以同样的速度顺时针沿着小圆圆周爬行。(本题圆周率π计算时取3)
(1)乙蚂蚁第一次爬回到C点时,需要多少秒?
(2)当乙蚂蚁第一次爬回到C点时,甲蚂蚁是否已经经过A点?
(3)甲乙两蚂蚊各自沿着圆周不间断地反复爬行,它们是否会在C点相遇?如果相遇,此时甲蚂蚁至少爬了几圈?如果不能相遇,请说明理由。
36.一辆自行车轮胎外直径50厘米,如果自行车每分钟转120周,这辆自行车每小时能行多少千米?(得数保留整千米)
37.(1)画一个直径是4厘米的圆并标出圆心和直径。
(2)如果把这个圆沿半径平均分成若干份,可以拼成一个近似的( )形。请你求出所拼成的这个图形的周长,把计算过程写在下面。
38.森林运动会上,蚂蚁、虫子要进行赛跑比赛。在猴子裁判画的跑道上,蚂蚁选择外圈的大圆跑道,而虫子选择内圈的小圆跑道。它们速度相同,并且都是同时从点A出发,沿着跑道回到点A。(1米、2米为小圆的直径长度)
(1)第一次比赛,蚂蚁、虫子在图1跑道上,蚂蚁在大圆按顺时针方向走一周,虫子在小圆按①→②→③→④方向回到点A。比赛结果是什么?请通过计算来验证你的结果。
(2)第二次比赛,蚂蚁、虫子在图2跑道上,蚂蚁在大圆按顺时针方向走一周,虫子在小圆按①→②→③→④→⑤→⑥方向回到点A。比赛结果是什么?请通过计算验证结果。
(3)通过两次比赛结果,你有什么发现?请你画图,并通过计算验证你的发现。
39.某赛车的左、右轮的距离是2m,转弯时,外侧的轮子比内侧的轮子要多行一些 路。当该赛车在下面的赛道上跑一圈时,外轮比内轮多行多少米
40.一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过2512米的桥,大约需要几分钟?(车身的长度忽略不计)
41.小明用绳子把4瓶矿泉水捆在一起(如下图),已知每瓶矿泉水的底面直径是6厘米,最后接头处用了12厘米,捆这4瓶矿泉水一共用了多少厘米的绳子?
42.一棵树的横截面近似是圆形。小强和小丽想测量出它的直径。他们拿一根长20米的绳子,绕6圈后还剩下1.16米。这棵树的直径是多少米?
43.一辆自行车的车轮直径是70厘米,自行车车轮每分钟转100周。要通过一座长2.198千米的大桥,需要几分钟?
44.如下图,两个连在一起的轮轴,小轮的半径是5分米,大轮转动2周,小轮转动10周,大轮的半径是多少分米?
45.淘气家离学校距离是1800米,他每天骑自行车回家,自行车车胎直径0.6米,如果自行车车轮平均每分钟转80圈,那么他10分钟从学校能回到家吗?
46.如图,笑笑和淘气分别从A,B处出发,沿半圆走到C,D。笑笑和淘气走过的路程相差多少米?
47.问题:学校运动场如图①,两端是半圆形,中间是正方形运动场,周长是257米.这个运动场的周长是多少米?
分析与解答:某小组采取合作学习的方式探究此问题,以下是该小组三位同学的对话:
甲:“把运动场进行平移变换(如图②),则圆的周长+正方形边长×2=运动场周长.”
乙:“圆的周长可以看作是正方形边长的3.14倍.”
丙:“我们可以用方程的思想来解决问题!”
亲爱的同学,请你帮助他们完成解答.
48.装卸工人把4根圆柱形钢管用铁丝捆扎在一起(如图)。钢管的横截面直径是10厘米,如果铁丝接头处的长度忽略不计,捆扎2圈,需要多长的铁丝?(π取3.14)
49.你见过像下面这样捆扎圆柱形物体的情形吗 仔细观察下,想一想:绕一周的绳子长度与圆柱的个数及其周长,直径有什么关系 (接头不计)
(1)图1绳子的长度=圆周长+ 条直径,图2绳子的长度=圆周长+ 条直径;你的初步发现是: 。
(2)如果把4个直径为10厘米的圆罐按照图3的样子捆两道(每道接头用8厘米),至少要多长的绳子 (得数保留整数)
小学数学六年级上册《圆的周长》专题经典易错题(通用版)参考答案
一、单选题
1.下图中从M到N,走路①与路②的结果是( C )。
A.路①远 B.路②远 C.一样远
2.自行车的前轮半径为30厘米,后轮半径为20厘米。如下图,当前轮向前行驶了5圈回到E点的位置时,后轮F点的位置是下图中的( C )。
A. B. C. D.
3.如图,把一支铅笔垂直插入一个半径为1cm的圆形硬纸板的圆心,然后绕一个直径为8cm的量角器的圆弧滚动,铅笔会留下痕迹,此痕迹的长是( C )cm。
A.12.56 B.20.7 C.15.7 D.28.26
4.一个半圆的周长是25.7cm,这个半圆的直径是( C )。
A.2.57cm B.5cm C.10cm D.314cm
5.下列关于圆的说法正确的是( B )。
A.半径确定圆的位置 B.圆是轴对称图形
C.圆周率是周长与半径的比值 D.圆的对称轴是直径
6.把一个周长是18.84分米的圆平均分成两个半圆,每个半圆的周长是( A )分米。
A.15.42 B.9.42 C.12.24 D.12.56
7.如图,六位朋友均匀的围坐在圆桌旁聚会,圆桌的半径为110cm,每人离桌边10cm,则图中相邻两人之间的圆弧的长(结果保留π)为( D )
A.10π cm B.20π cm C.30π cm D.40π cm
8.如图中有大、中、小三个圆,且中圆与小圆的直径之和等于大圆的直径,已知大圆周长比中圆周长长4π厘米,那么小圆半径是( C )厘米.(π为圆周率)
A.4 B.3 C.2 D.1
9.把一个周长为12.56cm的圆剪成两个半圆形,每个半圆形的周长是( C )cm。
A.12.56 B.6.28 C.10.28 D.25.12
10.如图,一台压路机的前轮直径是1.2米,如果前轮每分钟转6圈,压路机5分钟前进( A )米?
A.113.04 B.134.06 C.125.76 D.131.04
11.如下图,四个圆的圆心在一条直线上,大圆的周长与三个小圆的周长之和比较,结果是( C )。
A.大圆的周长较长 B.大圆的周长较短
C.相等 D.无法比较
12.从A到B,蚂蚁甲沿①号路线爬行,蚂蚁乙沿②号路线爬,如果它们的速度相同,它们爬行用的时间比,( B )。
A.甲用的时间多 B.一样 C.乙用的时间多
13.用一块长12米,宽7米的长方形铁皮剪半径是1.5米的圆,最多能剪( B )个.
A.11 B.8 C.10 D.13
14.把一张圆形纸片沿半径平均分成若干份,拼成一个近似长方形,其周长( B )。
A.等于圆周长 B.大于圆周长 C.小于圆周长 D.无法比较
15.一辆自行车的车轮半径是30厘米,这辆自行车通过一条1884米长的街道时,车轮要转大约( C )周.
A.10 B.100 C.1000 D.2000
二、判断题
16.一个圆形挂钟分针长10cm,这根分针的尖端15分钟所走的路程是15.7cm。( √ )
17.一个圆的周长是9.42米,剪成两个半圆后每个半圆的周长是4.71米.( × )
三、填空题
18.一个时钟的分针长10厘米,从8:00走到8:30,分针针尖走过了 31.4 厘米。
19.一个圆的半径扩大到原来的3倍后周长比原来多37.68厘米,原来圆的周长 18.84 厘米。
20.一个圆周长、直径、半径的和是27.84厘米,这个圆的半径是 3 厘米。
21.一个圆形花圃的直径是40米,李大爷每天早晨绕着花圃跑10圈,李大爷每天早晨大约跑 1256 米?如果沿着这个花圃的边线大约每隔5米种一棵杜鹃,大约可种 25 棵?
22.在标准400m跑道上,参加200m跑,每条跑道宽1.25m,相邻跑道中两人之间的起跑位置大约相差 3.925 m。(π取3.14)
23.一辆自行车的车轮半径是30cm,这辆自行车通过一条1413m长的街道时,车轮要转 750 圈。
24.(如图)一个半圆形花坛的周长是51.4米,半径是 10 米。
25.一张长18cm、宽15cm的长方形纸,最多可以剪 12 个周长12.56cm的圆。
26.如图,在长、宽分别为14cm,8cm的方框中,用一个半径为1cm的圆形纸片,无滑动地沿着方框按A-B-C-D-A的方向滚动。(本题中π的值取3)若纸片贴着方框内侧滚动一周回到出发位置,则圆心运动轨迹的长度是 36 cm,圆形纸片共转动了 6 圈。
27.量得一张DVD光盘的周长约是36cm,如果要做一个正方形袋子装这张光盘,那么这个正方形袋子的边长最少是 12 厘米.(π取3)
四、计算题
28.求阴影部分的周长。
(1)
(2)
(1)阴影部分的周长=8×2+3.14×8×2×
=16+3.14×4
=16+12.56
=28.56(dm);
(2)阴影部分的周长=10×2+3.14×10
=20+31.4
=51.4(cm);
五、解答题
29.小军骑车到学校需 几分?
解:70×3.14=219.8(厘米)
219.8×100=21980(厘米)
21980÷100=219.8(米)
2198÷219.8=10(分)
答:小军骑车到学校需10分。
30.一辆电动自行车的车轮直径是0.6米,如果每分转180周,这辆电动车5分钟可行多少米?
解:3.14×0.6×180×5
=1.884×180×5
=339.12×5
=1695.6(米)
答:这辆电动车5分钟可行1695.6米。
31.如图,有一只狗被拴在一个建筑物的墙角点A处,这个建筑物的底面是一个边长为8 m的正方形,拴狗的绳长18m。现在狗从点B出发,将绳拉紧并沿顺时针方向跑。狗最多可以跑多少米?
解:
×2×3.14×18+×2×3.14×(18-8)+×2×3.14×(18-8-8)
=28.26+15.7+3.14
=47.1(m)
答:狗最多可以跑47.1m。
32.大本钟——伦敦市的标志性建筑物.钟盘上时针的长度是2.75m。大本钟的时针经过6小时后,时针的尖端走过的路程是多少米?经过9小时呢?
解:2.75×2=5.5(米)
3.14×5.5×
=17.27×
=8.635(米)
3.14×5.5×
=17.27×
=12.9525(米))
答:经过6小时走过的路程是8.635米,经过9小时走过的路程是12.9525米。
33.自行车车轮的外直径约为0.75m,晓晓骑自行车通过一座长3768m的大桥,车轮每分钟转200周,通过这座大桥共需要多少分钟?
解:3768÷(3.14×0.75×200)
=3768÷(2.355×200)
=3768÷471
=8(分钟)
答:通过这座大桥共需要8分钟。
34.杂技演员表演独轮车走钢丝,车轮的直径是40cm。要骑过31.4m长的钢丝,车轮要转动多少圈?
解:40cm=0.4m
31.4÷(3.14×0.4)
=31.4÷1.256
=25(圈)
答:车轮要转动25圈。
35.如图,两个圆只有一个公共点C,大圆直径AC为50厘米,小圆直径BC为30厘米。甲、乙两只蚂蚁同时从C点出发,甲蚂蚁以每秒0.6厘米的速度顺时针沿着大圆圆周爬行,乙蚂蚁以同样的速度顺时针沿着小圆圆周爬行。(本题圆周率π计算时取3)
(1)乙蚂蚁第一次爬回到C点时,需要多少秒?
(2)当乙蚂蚁第一次爬回到C点时,甲蚂蚁是否已经经过A点?
(3)甲乙两蚂蚊各自沿着圆周不间断地反复爬行,它们是否会在C点相遇?如果相遇,此时甲蚂蚁至少爬了几圈?如果不能相遇,请说明理由。
(1)解:3×30÷0.6
=90÷0.6
=150(秒)
答:需要150秒。
(2)解:3×50÷2
=150÷2
=75(厘米)
75÷0.6=125(秒)
125秒<150秒
答:当乙蚂蚁第一次爬回到C点时,甲蚂蚁已经经过A点。
(3)解:125×2=250(秒)
150和250的最小公倍数是:2×5×5×3×5
=10×5×3×5
=50×3×5
=150×5
=750
750÷250=3(圈)
答:它们会在C点相遇,此时甲蚂蚁至少爬了3圈。
36.一辆自行车轮胎外直径50厘米,如果自行车每分钟转120周,这辆自行车每小时能行多少千米?(得数保留整千米)
解:3.14×50=157(厘米)
120×157=18840(厘米)=188.4(米)
188.4×60=11304(米)≈11(千米)
答:这辆自行车每小时能行11千米。
37.
(1)画一个直径是4厘米的圆并标出圆心和直径。
(2)如果把这个圆沿半径平均分成若干份,可以拼成一个近似的( )形。请你求出所拼成的这个图形的周长,把计算过程写在下面。
(1)解:如图所示:
(2)解:如果把这个圆沿半径平均分成若干份,可以拼成一个近似的长方形;
长:3.14×4÷2
=12.56÷2
=6.28(厘米)
宽:4÷2=2(厘米)
周长:(6.28+2)×2
=8.28×2
=16.56(厘米)
答:所拼成的这个图形的周长是16.56厘米。
38.森林运动会上,蚂蚁、虫子要进行赛跑比赛。在猴子裁判画的跑道上,蚂蚁选择外圈的大圆跑道,而虫子选择内圈的小圆跑道。它们速度相同,并且都是同时从点A出发,沿着跑道回到点A。(1米、2米为小圆的直径长度)
(1)第一次比赛,蚂蚁、虫子在图1跑道上,蚂蚁在大圆按顺时针方向走一周,虫子在小圆按①→②→③→④方向回到点A。比赛结果是什么?请通过计算来验证你的结果。
(2)第二次比赛,蚂蚁、虫子在图2跑道上,蚂蚁在大圆按顺时针方向走一周,虫子在小圆按①→②→③→④→⑤→⑥方向回到点A。比赛结果是什么?请通过计算验证结果。
(3)通过两次比赛结果,你有什么发现?请你画图,并通过计算验证你的发现。
(1)解:蚂蚁、虫子同时到达终点
蚂蚁:2×3.14×2=12.56(米)
虫子:3.14×2×2=12.56(米)
(2)解:虫子:3.14×1×2+3.14×2
=6.28+6.28
=12.56(米)
答:蚂蚁、虫子同时到达终点。
(3)解:小圆的周长之和等于大圆的周长。
大圆周长:2×3.14×2=12.56(米)
小圆周长和:3.14×1+3.14×3
=3.14+9.42
=12.56(米)
答:大圆周长=小圆周长的和。
39.某赛车的左、右轮的距离是2m,转弯时,外侧的轮子比内侧的轮子要多行一些 路。当该赛车在下面的赛道上跑一圈时,外轮比内轮多行多少米
解:3.14×(50+2×2)-3.14×50
=3.14×4
=12.56(米)
答: 外轮比内轮多行12.56米。
40.一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过2512米的桥,大约需要几分钟?(车身的长度忽略不计)
解:40÷100=0.4(米)
2512÷(3.14×0.4×2×100)
=2512÷(2.512×100)
=2512÷251.2
=10(分钟)
答:大约需要10分钟。
41.小明用绳子把4瓶矿泉水捆在一起(如下图),已知每瓶矿泉水的底面直径是6厘米,最后接头处用了12厘米,捆这4瓶矿泉水一共用了多少厘米的绳子?
解:3.14×6=18.84(厘米)
18.84+12=30.84(厘米)
30.84+6×4=54.84(厘米)
答:捆这4瓶矿泉水一共用了54.84厘米的绳子。
42.一棵树的横截面近似是圆形。小强和小丽想测量出它的直径。他们拿一根长20米的绳子,绕6圈后还剩下1.16米。这棵树的直径是多少米?
解:20-1.16=18.84(米)
18.84÷6=3.14(米)
3.14÷3.14=1(米)
答:这棵树的直径是1米。
43.一辆自行车的车轮直径是70厘米,自行车车轮每分钟转100周。要通过一座长2.198千米的大桥,需要几分钟?
解:2.198×1000=2198(米)
70÷100=0.7(米)
3.14×0.7×100
=2.198×100
=219.8(米)
2198÷219.8=10(分)
答: 需要10分钟 。
44.如下图,两个连在一起的轮轴,小轮的半径是5分米,大轮转动2周,小轮转动10周,大轮的半径是多少分米?
解:2×5×3.14×10÷2÷3.14÷2
=10×3.14×10÷2÷3.14÷2
=31.4×10÷2÷3.14÷2
=314÷2÷3.14÷2
=157÷3.14÷2
=50÷2
=25(分米)
答: 大轮的半径是25分米 。
45.淘气家离学校距离是1800米,他每天骑自行车回家,自行车车胎直径0.6米,如果自行车车轮平均每分钟转80圈,那么他10分钟从学校能回到家吗?
1800÷(3.14×0.6×80)=1800÷150.72≈12(分钟)
12>10
答: 他10分钟从学校不能回到家。
46.如图,笑笑和淘气分别从A,B处出发,沿半圆走到C,D。笑笑和淘气走过的路程相差多少米?
解:3.14×(10+1)-3.14×10
=3.14×11-3.14×10
=3.14×(11-10)
=3.14(米)
答:笑笑和淘气走过的路程相差3.14米。
47.问题:学校运动场如图①,两端是半圆形,中间是正方形运动场,周长是257米.这个运动场的周长是多少米?
分析与解答:某小组采取合作学习的方式探究此问题,以下是该小组三位同学的对话:
甲:“把运动场进行平移变换(如图②),则圆的周长+正方形边长×2=运动场周长.”
乙:“圆的周长可以看作是正方形边长的3.14倍.”
丙:“我们可以用方程的思想来解决问题!”
亲爱的同学,请你帮助他们完成解答.
(1)解:①257÷4=64.25(米)
3.14×64.25+64.25×2
=201.745+128.5
=330.245(米)
②257÷4×3.14+257÷4×2
=201.745+128.5
=330.245(米)
③设正方形的边长为x米,
4x=257
x=257÷4
x=64.25
64.25×3.14+64.25×2
=201.745+128.5
=330.245(米)
答:这个运动场的周长是330.245米。
48.装卸工人把4根圆柱形钢管用铁丝捆扎在一起(如图)。钢管的横截面直径是10厘米,如果铁丝接头处的长度忽略不计,捆扎2圈,需要多长的铁丝?(π取3.14)
解:(10×4+3.14×10)×2
=(40+31.4)×2
=71.4×2
=142.8(厘米)
答:需要142.8厘米长的铁丝。
49.你见过像下面这样捆扎圆柱形物体的情形吗 仔细观察下,想一想:绕一周的绳子长度与圆柱的个数及其周长,直径有什么关系 (接头不计)
(1)图1绳子的长度=圆周长+ 条直径,图2绳子的长度=圆周长+ 条直径;你的初步发现是: 。
(2)如果把4个直径为10厘米的圆罐按照图3的样子捆两道(每道接头用8厘米),至少要多长的绳子 (得数保留整数)
(1)2;3;无论有几个圆柱堆砌,曲线部分之和都是一个圆的周长,绕一周的绳子长度=圆的周长+圆柱的个数×直径。
(2)(3.14×10+10×4)×2+8×2
=(31.4+40)×2+8×2
=71.4×2+16
=142.8+16
=158.8(厘米)
≈159(厘米)
答:至少需要159厘米的绳子
一、单选题
1.下图中从M到N,走路①与路②的结果是( )。
A.路①远 B.路②远 C.一样远
2.自行车的前轮半径为30厘米,后轮半径为20厘米。如下图,当前轮向前行驶了5圈回到E点的位置时,后轮F点的位置是下图中的( )。
A. B. C. D.
3.如图,把一支铅笔垂直插入一个半径为1cm的圆形硬纸板的圆心,然后绕一个直径为8cm的量角器的圆弧滚动,铅笔会留下痕迹,此痕迹的长是( )cm。
A.12.56 B.20.7 C.15.7 D.28.26
4.一个半圆的周长是25.7cm,这个半圆的直径是( )。
A.2.57cm B.5cm C.10cm D.314cm
5.下列关于圆的说法正确的是( )。
A.半径确定圆的位置 B.圆是轴对称图形
C.圆周率是周长与半径的比值 D.圆的对称轴是直径
6.把一个周长是18.84分米的圆平均分成两个半圆,每个半圆的周长是( )分米。
A.15.42 B.9.42 C.12.24 D.12.56
7.如图,六位朋友均匀的围坐在圆桌旁聚会,圆桌的半径为110cm,每人离桌边10cm,则图中相邻两人之间的圆弧的长(结果保留π)为( )
A.10π cm B.20π cm C.30π cm D.40π cm
8.如图中有大、中、小三个圆,且中圆与小圆的直径之和等于大圆的直径,已知大圆周长比中圆周长长4π厘米,那么小圆半径是( )厘米.(π为圆周率)
A.4 B.3 C.2 D.1
9.把一个周长为12.56cm的圆剪成两个半圆形,每个半圆形的周长是( )cm。
A.12.56 B.6.28 C.10.28 D.25.12
10.如图,一台压路机的前轮直径是1.2米,如果前轮每分钟转6圈,压路机5分钟前进 米?
A.113.04 B.134.06 C.125.76 D.131.04
11.如下图,四个圆的圆心在一条直线上,大圆的周长与三个小圆的周长之和比较,结果是( )。
A.大圆的周长较长 B.大圆的周长较短
C.相等 D.无法比较
12.从A到B,蚂蚁甲沿①号路线爬行,蚂蚁乙沿②号路线爬,如果它们的速度相同,它们爬行用的时间比,( )。
A.甲用的时间多 B.一样 C.乙用的时间多
13.用一块长12米,宽7米的长方形铁皮剪半径是1.5米的圆,最多能剪( )个.
A.11 B.8 C.10 D.13
14.把一张圆形纸片沿半径平均分成若干份,拼成一个近似长方形,其周长( )。
A.等于圆周长 B.大于圆周长 C.小于圆周长 D.无法比较
15.一辆自行车的车轮半径是30厘米,这辆自行车通过一条1884米长的街道时,车轮要转大约( )周.
A.10 B.100 C.1000 D.2000
二、判断题
16.一个圆形挂钟分针长10cm,这根分针的尖端15分钟所走的路程是15.7cm。( )
17.一个圆的周长是9.42米,剪成两个半圆后每个半圆的周长是4.71米.( )
三、填空题
18.一个时钟的分针长10厘米,从8:00走到8:30,分针针尖走过了 厘米。
19.一个圆的半径扩大到原来的3倍后周长比原来多37.68厘米,原来圆的周长 厘米。
20.一个圆周长、直径、半径的和是27.84厘米,这个圆的半径是 厘米。
21.一个圆形花圃的直径是40米,李大爷每天早晨绕着花圃跑10圈,李大爷每天早晨大约跑 米?如果沿着这个花圃的边线大约每隔5米种一棵杜鹃,大约可种 棵?
22.在标准400m跑道上,参加200m跑,每条跑道宽1.25m,相邻跑道中两人之间的起跑位置大约相差 m。(π取3.14)
23.一辆自行车的车轮半径是30cm,这辆自行车通过一条1413m长的街道时,车轮要转 圈。
24.(如图)一个半圆形花坛的周长是51.4米,半径是 米。
25.一张长18cm、宽15cm的长方形纸,最多可以剪 个周长12.56cm的圆。
26.如图,在长、宽分别为14cm,8cm的方框中,用一个半径为1cm的圆形纸片,无滑动地沿着方框按A-B-C-D-A的方向滚动。(本题中π的值取3)若纸片贴着方框内侧滚动一周回到出发位置,则圆心运动轨迹的长度是 cm,圆形纸片共转动了 圈。
27.量得一张DVD光盘的周长约是36cm,如果要做一个正方形袋子装这张光盘,那么这个正方形袋子的边长最少是 厘米.(π取3)
四、计算题
28.求阴影部分的周长。
(1)
(2)
五、解答题
29.小军骑车到学校需 几分?
30.一辆电动自行车的车轮直径是0.6米,如果每分转180周,这辆电动车5分钟可行多少米?
31.如图,有一只狗被拴在一个建筑物的墙角点A处,这个建筑物的底面是一个边长为8 m的正方形,拴狗的绳长18m。现在狗从点B出发,将绳拉紧并沿顺时针方向跑。狗最多可以跑多少米?
32.大本钟——伦敦市的标志性建筑物.钟盘上时针的长度是2.75m。大本钟的时针经过6小时后,时针的尖端走过的路程是多少米?经过9小时呢?
33.自行车车轮的外直径约为0.75m,晓晓骑自行车通过一座长3768m的大桥,车轮每分钟转200周,通过这座大桥共需要多少分钟?
34.杂技演员表演独轮车走钢丝,车轮的直径是40cm。要骑过31.4m长的钢丝,车轮要转动多少圈?
35.如图,两个圆只有一个公共点C,大圆直径AC为50厘米,小圆直径BC为30厘米。甲、乙两只蚂蚁同时从C点出发,甲蚂蚁以每秒0.6厘米的速度顺时针沿着大圆圆周爬行,乙蚂蚁以同样的速度顺时针沿着小圆圆周爬行。(本题圆周率π计算时取3)
(1)乙蚂蚁第一次爬回到C点时,需要多少秒?
(2)当乙蚂蚁第一次爬回到C点时,甲蚂蚁是否已经经过A点?
(3)甲乙两蚂蚊各自沿着圆周不间断地反复爬行,它们是否会在C点相遇?如果相遇,此时甲蚂蚁至少爬了几圈?如果不能相遇,请说明理由。
36.一辆自行车轮胎外直径50厘米,如果自行车每分钟转120周,这辆自行车每小时能行多少千米?(得数保留整千米)
37.(1)画一个直径是4厘米的圆并标出圆心和直径。
(2)如果把这个圆沿半径平均分成若干份,可以拼成一个近似的( )形。请你求出所拼成的这个图形的周长,把计算过程写在下面。
38.森林运动会上,蚂蚁、虫子要进行赛跑比赛。在猴子裁判画的跑道上,蚂蚁选择外圈的大圆跑道,而虫子选择内圈的小圆跑道。它们速度相同,并且都是同时从点A出发,沿着跑道回到点A。(1米、2米为小圆的直径长度)
(1)第一次比赛,蚂蚁、虫子在图1跑道上,蚂蚁在大圆按顺时针方向走一周,虫子在小圆按①→②→③→④方向回到点A。比赛结果是什么?请通过计算来验证你的结果。
(2)第二次比赛,蚂蚁、虫子在图2跑道上,蚂蚁在大圆按顺时针方向走一周,虫子在小圆按①→②→③→④→⑤→⑥方向回到点A。比赛结果是什么?请通过计算验证结果。
(3)通过两次比赛结果,你有什么发现?请你画图,并通过计算验证你的发现。
39.某赛车的左、右轮的距离是2m,转弯时,外侧的轮子比内侧的轮子要多行一些 路。当该赛车在下面的赛道上跑一圈时,外轮比内轮多行多少米
40.一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过2512米的桥,大约需要几分钟?(车身的长度忽略不计)
41.小明用绳子把4瓶矿泉水捆在一起(如下图),已知每瓶矿泉水的底面直径是6厘米,最后接头处用了12厘米,捆这4瓶矿泉水一共用了多少厘米的绳子?
42.一棵树的横截面近似是圆形。小强和小丽想测量出它的直径。他们拿一根长20米的绳子,绕6圈后还剩下1.16米。这棵树的直径是多少米?
43.一辆自行车的车轮直径是70厘米,自行车车轮每分钟转100周。要通过一座长2.198千米的大桥,需要几分钟?
44.如下图,两个连在一起的轮轴,小轮的半径是5分米,大轮转动2周,小轮转动10周,大轮的半径是多少分米?
45.淘气家离学校距离是1800米,他每天骑自行车回家,自行车车胎直径0.6米,如果自行车车轮平均每分钟转80圈,那么他10分钟从学校能回到家吗?
46.如图,笑笑和淘气分别从A,B处出发,沿半圆走到C,D。笑笑和淘气走过的路程相差多少米?
47.问题:学校运动场如图①,两端是半圆形,中间是正方形运动场,周长是257米.这个运动场的周长是多少米?
分析与解答:某小组采取合作学习的方式探究此问题,以下是该小组三位同学的对话:
甲:“把运动场进行平移变换(如图②),则圆的周长+正方形边长×2=运动场周长.”
乙:“圆的周长可以看作是正方形边长的3.14倍.”
丙:“我们可以用方程的思想来解决问题!”
亲爱的同学,请你帮助他们完成解答.
48.装卸工人把4根圆柱形钢管用铁丝捆扎在一起(如图)。钢管的横截面直径是10厘米,如果铁丝接头处的长度忽略不计,捆扎2圈,需要多长的铁丝?(π取3.14)
49.你见过像下面这样捆扎圆柱形物体的情形吗 仔细观察下,想一想:绕一周的绳子长度与圆柱的个数及其周长,直径有什么关系 (接头不计)
(1)图1绳子的长度=圆周长+ 条直径,图2绳子的长度=圆周长+ 条直径;你的初步发现是: 。
(2)如果把4个直径为10厘米的圆罐按照图3的样子捆两道(每道接头用8厘米),至少要多长的绳子 (得数保留整数)
小学数学六年级上册《圆的周长》专题经典易错题(通用版)参考答案
一、单选题
1.下图中从M到N,走路①与路②的结果是( C )。
A.路①远 B.路②远 C.一样远
2.自行车的前轮半径为30厘米,后轮半径为20厘米。如下图,当前轮向前行驶了5圈回到E点的位置时,后轮F点的位置是下图中的( C )。
A. B. C. D.
3.如图,把一支铅笔垂直插入一个半径为1cm的圆形硬纸板的圆心,然后绕一个直径为8cm的量角器的圆弧滚动,铅笔会留下痕迹,此痕迹的长是( C )cm。
A.12.56 B.20.7 C.15.7 D.28.26
4.一个半圆的周长是25.7cm,这个半圆的直径是( C )。
A.2.57cm B.5cm C.10cm D.314cm
5.下列关于圆的说法正确的是( B )。
A.半径确定圆的位置 B.圆是轴对称图形
C.圆周率是周长与半径的比值 D.圆的对称轴是直径
6.把一个周长是18.84分米的圆平均分成两个半圆,每个半圆的周长是( A )分米。
A.15.42 B.9.42 C.12.24 D.12.56
7.如图,六位朋友均匀的围坐在圆桌旁聚会,圆桌的半径为110cm,每人离桌边10cm,则图中相邻两人之间的圆弧的长(结果保留π)为( D )
A.10π cm B.20π cm C.30π cm D.40π cm
8.如图中有大、中、小三个圆,且中圆与小圆的直径之和等于大圆的直径,已知大圆周长比中圆周长长4π厘米,那么小圆半径是( C )厘米.(π为圆周率)
A.4 B.3 C.2 D.1
9.把一个周长为12.56cm的圆剪成两个半圆形,每个半圆形的周长是( C )cm。
A.12.56 B.6.28 C.10.28 D.25.12
10.如图,一台压路机的前轮直径是1.2米,如果前轮每分钟转6圈,压路机5分钟前进( A )米?
A.113.04 B.134.06 C.125.76 D.131.04
11.如下图,四个圆的圆心在一条直线上,大圆的周长与三个小圆的周长之和比较,结果是( C )。
A.大圆的周长较长 B.大圆的周长较短
C.相等 D.无法比较
12.从A到B,蚂蚁甲沿①号路线爬行,蚂蚁乙沿②号路线爬,如果它们的速度相同,它们爬行用的时间比,( B )。
A.甲用的时间多 B.一样 C.乙用的时间多
13.用一块长12米,宽7米的长方形铁皮剪半径是1.5米的圆,最多能剪( B )个.
A.11 B.8 C.10 D.13
14.把一张圆形纸片沿半径平均分成若干份,拼成一个近似长方形,其周长( B )。
A.等于圆周长 B.大于圆周长 C.小于圆周长 D.无法比较
15.一辆自行车的车轮半径是30厘米,这辆自行车通过一条1884米长的街道时,车轮要转大约( C )周.
A.10 B.100 C.1000 D.2000
二、判断题
16.一个圆形挂钟分针长10cm,这根分针的尖端15分钟所走的路程是15.7cm。( √ )
17.一个圆的周长是9.42米,剪成两个半圆后每个半圆的周长是4.71米.( × )
三、填空题
18.一个时钟的分针长10厘米,从8:00走到8:30,分针针尖走过了 31.4 厘米。
19.一个圆的半径扩大到原来的3倍后周长比原来多37.68厘米,原来圆的周长 18.84 厘米。
20.一个圆周长、直径、半径的和是27.84厘米,这个圆的半径是 3 厘米。
21.一个圆形花圃的直径是40米,李大爷每天早晨绕着花圃跑10圈,李大爷每天早晨大约跑 1256 米?如果沿着这个花圃的边线大约每隔5米种一棵杜鹃,大约可种 25 棵?
22.在标准400m跑道上,参加200m跑,每条跑道宽1.25m,相邻跑道中两人之间的起跑位置大约相差 3.925 m。(π取3.14)
23.一辆自行车的车轮半径是30cm,这辆自行车通过一条1413m长的街道时,车轮要转 750 圈。
24.(如图)一个半圆形花坛的周长是51.4米,半径是 10 米。
25.一张长18cm、宽15cm的长方形纸,最多可以剪 12 个周长12.56cm的圆。
26.如图,在长、宽分别为14cm,8cm的方框中,用一个半径为1cm的圆形纸片,无滑动地沿着方框按A-B-C-D-A的方向滚动。(本题中π的值取3)若纸片贴着方框内侧滚动一周回到出发位置,则圆心运动轨迹的长度是 36 cm,圆形纸片共转动了 6 圈。
27.量得一张DVD光盘的周长约是36cm,如果要做一个正方形袋子装这张光盘,那么这个正方形袋子的边长最少是 12 厘米.(π取3)
四、计算题
28.求阴影部分的周长。
(1)
(2)
(1)阴影部分的周长=8×2+3.14×8×2×
=16+3.14×4
=16+12.56
=28.56(dm);
(2)阴影部分的周长=10×2+3.14×10
=20+31.4
=51.4(cm);
五、解答题
29.小军骑车到学校需 几分?
解:70×3.14=219.8(厘米)
219.8×100=21980(厘米)
21980÷100=219.8(米)
2198÷219.8=10(分)
答:小军骑车到学校需10分。
30.一辆电动自行车的车轮直径是0.6米,如果每分转180周,这辆电动车5分钟可行多少米?
解:3.14×0.6×180×5
=1.884×180×5
=339.12×5
=1695.6(米)
答:这辆电动车5分钟可行1695.6米。
31.如图,有一只狗被拴在一个建筑物的墙角点A处,这个建筑物的底面是一个边长为8 m的正方形,拴狗的绳长18m。现在狗从点B出发,将绳拉紧并沿顺时针方向跑。狗最多可以跑多少米?
解:
×2×3.14×18+×2×3.14×(18-8)+×2×3.14×(18-8-8)
=28.26+15.7+3.14
=47.1(m)
答:狗最多可以跑47.1m。
32.大本钟——伦敦市的标志性建筑物.钟盘上时针的长度是2.75m。大本钟的时针经过6小时后,时针的尖端走过的路程是多少米?经过9小时呢?
解:2.75×2=5.5(米)
3.14×5.5×
=17.27×
=8.635(米)
3.14×5.5×
=17.27×
=12.9525(米))
答:经过6小时走过的路程是8.635米,经过9小时走过的路程是12.9525米。
33.自行车车轮的外直径约为0.75m,晓晓骑自行车通过一座长3768m的大桥,车轮每分钟转200周,通过这座大桥共需要多少分钟?
解:3768÷(3.14×0.75×200)
=3768÷(2.355×200)
=3768÷471
=8(分钟)
答:通过这座大桥共需要8分钟。
34.杂技演员表演独轮车走钢丝,车轮的直径是40cm。要骑过31.4m长的钢丝,车轮要转动多少圈?
解:40cm=0.4m
31.4÷(3.14×0.4)
=31.4÷1.256
=25(圈)
答:车轮要转动25圈。
35.如图,两个圆只有一个公共点C,大圆直径AC为50厘米,小圆直径BC为30厘米。甲、乙两只蚂蚁同时从C点出发,甲蚂蚁以每秒0.6厘米的速度顺时针沿着大圆圆周爬行,乙蚂蚁以同样的速度顺时针沿着小圆圆周爬行。(本题圆周率π计算时取3)
(1)乙蚂蚁第一次爬回到C点时,需要多少秒?
(2)当乙蚂蚁第一次爬回到C点时,甲蚂蚁是否已经经过A点?
(3)甲乙两蚂蚊各自沿着圆周不间断地反复爬行,它们是否会在C点相遇?如果相遇,此时甲蚂蚁至少爬了几圈?如果不能相遇,请说明理由。
(1)解:3×30÷0.6
=90÷0.6
=150(秒)
答:需要150秒。
(2)解:3×50÷2
=150÷2
=75(厘米)
75÷0.6=125(秒)
125秒<150秒
答:当乙蚂蚁第一次爬回到C点时,甲蚂蚁已经经过A点。
(3)解:125×2=250(秒)
150和250的最小公倍数是:2×5×5×3×5
=10×5×3×5
=50×3×5
=150×5
=750
750÷250=3(圈)
答:它们会在C点相遇,此时甲蚂蚁至少爬了3圈。
36.一辆自行车轮胎外直径50厘米,如果自行车每分钟转120周,这辆自行车每小时能行多少千米?(得数保留整千米)
解:3.14×50=157(厘米)
120×157=18840(厘米)=188.4(米)
188.4×60=11304(米)≈11(千米)
答:这辆自行车每小时能行11千米。
37.
(1)画一个直径是4厘米的圆并标出圆心和直径。
(2)如果把这个圆沿半径平均分成若干份,可以拼成一个近似的( )形。请你求出所拼成的这个图形的周长,把计算过程写在下面。
(1)解:如图所示:
(2)解:如果把这个圆沿半径平均分成若干份,可以拼成一个近似的长方形;
长:3.14×4÷2
=12.56÷2
=6.28(厘米)
宽:4÷2=2(厘米)
周长:(6.28+2)×2
=8.28×2
=16.56(厘米)
答:所拼成的这个图形的周长是16.56厘米。
38.森林运动会上,蚂蚁、虫子要进行赛跑比赛。在猴子裁判画的跑道上,蚂蚁选择外圈的大圆跑道,而虫子选择内圈的小圆跑道。它们速度相同,并且都是同时从点A出发,沿着跑道回到点A。(1米、2米为小圆的直径长度)
(1)第一次比赛,蚂蚁、虫子在图1跑道上,蚂蚁在大圆按顺时针方向走一周,虫子在小圆按①→②→③→④方向回到点A。比赛结果是什么?请通过计算来验证你的结果。
(2)第二次比赛,蚂蚁、虫子在图2跑道上,蚂蚁在大圆按顺时针方向走一周,虫子在小圆按①→②→③→④→⑤→⑥方向回到点A。比赛结果是什么?请通过计算验证结果。
(3)通过两次比赛结果,你有什么发现?请你画图,并通过计算验证你的发现。
(1)解:蚂蚁、虫子同时到达终点
蚂蚁:2×3.14×2=12.56(米)
虫子:3.14×2×2=12.56(米)
(2)解:虫子:3.14×1×2+3.14×2
=6.28+6.28
=12.56(米)
答:蚂蚁、虫子同时到达终点。
(3)解:小圆的周长之和等于大圆的周长。
大圆周长:2×3.14×2=12.56(米)
小圆周长和:3.14×1+3.14×3
=3.14+9.42
=12.56(米)
答:大圆周长=小圆周长的和。
39.某赛车的左、右轮的距离是2m,转弯时,外侧的轮子比内侧的轮子要多行一些 路。当该赛车在下面的赛道上跑一圈时,外轮比内轮多行多少米
解:3.14×(50+2×2)-3.14×50
=3.14×4
=12.56(米)
答: 外轮比内轮多行12.56米。
40.一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过2512米的桥,大约需要几分钟?(车身的长度忽略不计)
解:40÷100=0.4(米)
2512÷(3.14×0.4×2×100)
=2512÷(2.512×100)
=2512÷251.2
=10(分钟)
答:大约需要10分钟。
41.小明用绳子把4瓶矿泉水捆在一起(如下图),已知每瓶矿泉水的底面直径是6厘米,最后接头处用了12厘米,捆这4瓶矿泉水一共用了多少厘米的绳子?
解:3.14×6=18.84(厘米)
18.84+12=30.84(厘米)
30.84+6×4=54.84(厘米)
答:捆这4瓶矿泉水一共用了54.84厘米的绳子。
42.一棵树的横截面近似是圆形。小强和小丽想测量出它的直径。他们拿一根长20米的绳子,绕6圈后还剩下1.16米。这棵树的直径是多少米?
解:20-1.16=18.84(米)
18.84÷6=3.14(米)
3.14÷3.14=1(米)
答:这棵树的直径是1米。
43.一辆自行车的车轮直径是70厘米,自行车车轮每分钟转100周。要通过一座长2.198千米的大桥,需要几分钟?
解:2.198×1000=2198(米)
70÷100=0.7(米)
3.14×0.7×100
=2.198×100
=219.8(米)
2198÷219.8=10(分)
答: 需要10分钟 。
44.如下图,两个连在一起的轮轴,小轮的半径是5分米,大轮转动2周,小轮转动10周,大轮的半径是多少分米?
解:2×5×3.14×10÷2÷3.14÷2
=10×3.14×10÷2÷3.14÷2
=31.4×10÷2÷3.14÷2
=314÷2÷3.14÷2
=157÷3.14÷2
=50÷2
=25(分米)
答: 大轮的半径是25分米 。
45.淘气家离学校距离是1800米,他每天骑自行车回家,自行车车胎直径0.6米,如果自行车车轮平均每分钟转80圈,那么他10分钟从学校能回到家吗?
1800÷(3.14×0.6×80)=1800÷150.72≈12(分钟)
12>10
答: 他10分钟从学校不能回到家。
46.如图,笑笑和淘气分别从A,B处出发,沿半圆走到C,D。笑笑和淘气走过的路程相差多少米?
解:3.14×(10+1)-3.14×10
=3.14×11-3.14×10
=3.14×(11-10)
=3.14(米)
答:笑笑和淘气走过的路程相差3.14米。
47.问题:学校运动场如图①,两端是半圆形,中间是正方形运动场,周长是257米.这个运动场的周长是多少米?
分析与解答:某小组采取合作学习的方式探究此问题,以下是该小组三位同学的对话:
甲:“把运动场进行平移变换(如图②),则圆的周长+正方形边长×2=运动场周长.”
乙:“圆的周长可以看作是正方形边长的3.14倍.”
丙:“我们可以用方程的思想来解决问题!”
亲爱的同学,请你帮助他们完成解答.
(1)解:①257÷4=64.25(米)
3.14×64.25+64.25×2
=201.745+128.5
=330.245(米)
②257÷4×3.14+257÷4×2
=201.745+128.5
=330.245(米)
③设正方形的边长为x米,
4x=257
x=257÷4
x=64.25
64.25×3.14+64.25×2
=201.745+128.5
=330.245(米)
答:这个运动场的周长是330.245米。
48.装卸工人把4根圆柱形钢管用铁丝捆扎在一起(如图)。钢管的横截面直径是10厘米,如果铁丝接头处的长度忽略不计,捆扎2圈,需要多长的铁丝?(π取3.14)
解:(10×4+3.14×10)×2
=(40+31.4)×2
=71.4×2
=142.8(厘米)
答:需要142.8厘米长的铁丝。
49.你见过像下面这样捆扎圆柱形物体的情形吗 仔细观察下,想一想:绕一周的绳子长度与圆柱的个数及其周长,直径有什么关系 (接头不计)
(1)图1绳子的长度=圆周长+ 条直径,图2绳子的长度=圆周长+ 条直径;你的初步发现是: 。
(2)如果把4个直径为10厘米的圆罐按照图3的样子捆两道(每道接头用8厘米),至少要多长的绳子 (得数保留整数)
(1)2;3;无论有几个圆柱堆砌,曲线部分之和都是一个圆的周长,绕一周的绳子长度=圆的周长+圆柱的个数×直径。
(2)(3.14×10+10×4)×2+8×2
=(31.4+40)×2+8×2
=71.4×2+16
=142.8+16
=158.8(厘米)
≈159(厘米)
答:至少需要159厘米的绳子
