4.3.2线段的长短比较 课件(共19张PPT)
文档属性
| 名称 | 4.3.2线段的长短比较 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 348.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
4.3 线段的长短比较
探究新知
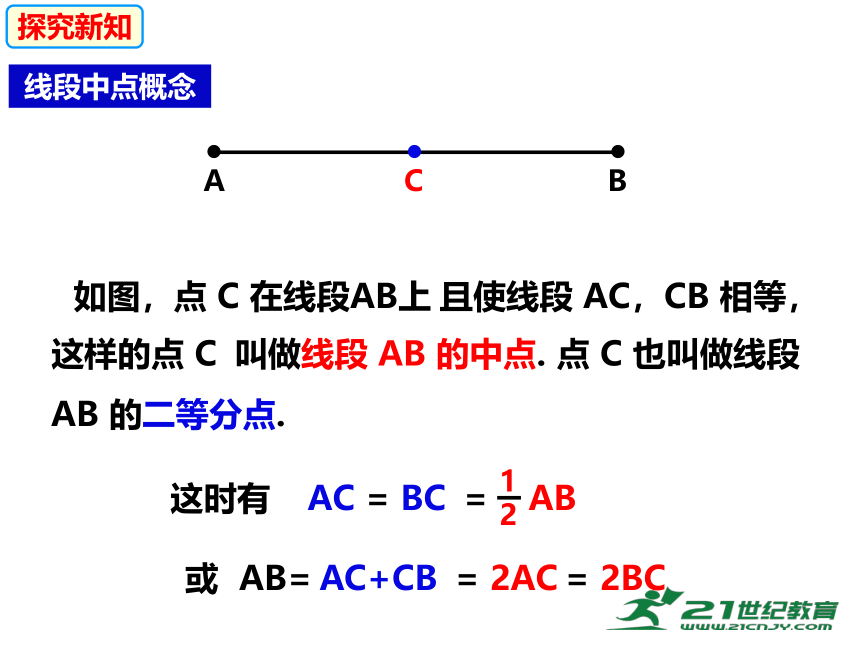
线段中点概念
A
B
C
点 C 也叫做线段
如图,点 C 在线段AB上
且使线段 AC,CB 相等,
这样的点 C
叫做线段 AB 的中点.
AB 的二等分点.
AC = BC
或
这时有
1
2
= AB
AB=
AC+CB
= 2AC
= 2BC
探究新知
C
A
B
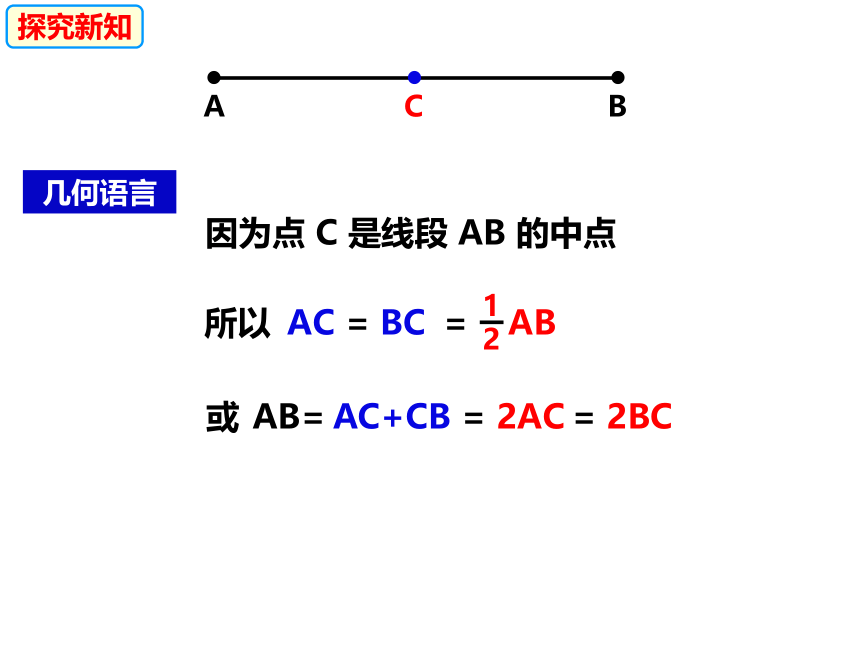
几何语言
AC = BC
或
所以
1
2
= AB
AB=
AC+CB
= 2AC
= 2BC
因为点 C 是线段 AB 的中点
两点之间线段最短
三
思考 2 如上图,人们修建公路遇到大山阻碍时,为什么时常打通一条穿越大山的直的隧道?
思考 1 如图,从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地的最短道路?如果能,请你在图上画出最短路线.
A
B
两点之间的所有连线中,线段最短.
上面问题,反映了线段有如下的基本事实:
你知道吗?
简述:两点之间线段最短.
两点之间线段的长度,
叫做这两点之间的距离.
方法点拨:
距离是指线段的长度,是一个具有单位的数值,而不是线段本身,线段本身是图形.
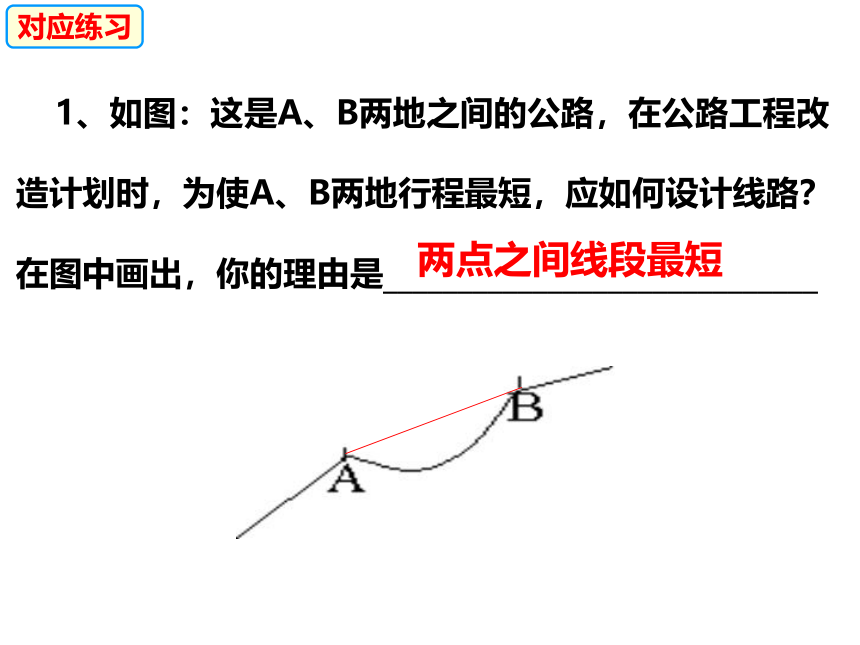
1、如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出,你的理由是_____________________________
两点之间线段最短
对应练习
2、如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
对应练习
A.A→C→D→B B.A→C→F→B C.A→C→E→F→B D.A→C→M→B
B
3、如图点A、B表示两个居民小区,它们分别位于公路MN的两侧,现要在公路边建造一个车站C,使A、B两地居民小区的人乘车所走路程之和最短,那么车站应该建在什么地方?为什么?
A
B
M
N
对应练习
C
A
B
C
D
4、如图,有A、B、C、D四个村庄,这四个村庄要共建一个自来水塔,要求用水管最省.请问自来水塔应建在何处?
E
对应练习
对应练习
5、下列四个生活、生产现象:
① 用两个钉子就可以把木条固定在墙上;
② 植树时,只要定出两棵树的位置,就能确定同一行所在的直线;
③ 从A地到B地,架设电线,总是尽可能沿着线段AB架设;
④ 把弯曲的公路改直,就能缩短路程.其中可用定理“两点之间,线段最短”来解释的现象有 .(填序号)
①③
对应练习
6、平面上有 A,B 两点,且 AB=7cm.
(1) 若在该平面上找一点 C,使 CA+CB=7cm,则点 C 在何处?
(2) 若使 CA+CB>7cm,则点 C 在何处?
(3) 若使 CA+CB<7cm,存在这样的点C吗?
对应练习
7、已知点 B 在直线 AC 上,AB=4cm,AC=6cm,P,Q 分别是 AB,AC 的中点,求线段 PQ 的长.
对应练习
8、如图,B、C 两点把线段 MN 分成三部分,其比为 MB:BC:CN=2:3:4,点 P 是 MN 的中点,PC=2cm,求 MN 的长.
对应练习
9、如图,已知点 D 是线段 AB 上的一点,延长线段AB 至 C,使得 AB=BC,且 DC=5AD,若 BD=4cm,求线段 AC 的长.
对应练习
10、如图,已知线段 AB 和 CD 的公共部分 BD= AB= CD,线段 AB、CD 的中点 E、F 之间距离是 10cm,求AB,CD的长.
1
3
1
4
对应练习
11、线段 AB 上有两点 P,Q ,点 P 将 AB 分成两部分,AP:PB=2:3;点 Q 将 AB 也分成两部分,AQ:QB=4:1;且 PQ=3cm.求 AP,QB的长.
对应练习
12、如图,线段 AB=4,点 O 是线段 AB 上一点,C,D 分别是线段 OA,OB 的中点.
(1) 求线段 CD 的长.
(2) 若把“点O是线段AB上一点”改为“点O是线段AB延长线上一点”,其他条件不变,请你画出图形,并求出CD的长.
C
A
B
D
O
对应练习
13、 如图在数轴上有A,B两点,点A表示的数为-10,点O表示的数为0,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动,点N以每秒2个单位长度的速度从点O向右运动(点M,点N同时出发).
(1) 数轴上点B表示的数是 .
(2) 经过几秒,点M,N到原点的距离相等?
(3) 点N在点B左侧运动的情况下,当点M运动到什么位置时恰好使AM=2BN?
本节课你有什么收获?
4.3 线段的长短比较
探究新知
线段中点概念
A
B
C
点 C 也叫做线段
如图,点 C 在线段AB上
且使线段 AC,CB 相等,
这样的点 C
叫做线段 AB 的中点.
AB 的二等分点.
AC = BC
或
这时有
1
2
= AB
AB=
AC+CB
= 2AC
= 2BC
探究新知
C
A
B
几何语言
AC = BC
或
所以
1
2
= AB
AB=
AC+CB
= 2AC
= 2BC
因为点 C 是线段 AB 的中点
两点之间线段最短
三
思考 2 如上图,人们修建公路遇到大山阻碍时,为什么时常打通一条穿越大山的直的隧道?
思考 1 如图,从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地的最短道路?如果能,请你在图上画出最短路线.
A
B
两点之间的所有连线中,线段最短.
上面问题,反映了线段有如下的基本事实:
你知道吗?
简述:两点之间线段最短.
两点之间线段的长度,
叫做这两点之间的距离.
方法点拨:
距离是指线段的长度,是一个具有单位的数值,而不是线段本身,线段本身是图形.
1、如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出,你的理由是_____________________________
两点之间线段最短
对应练习
2、如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
对应练习
A.A→C→D→B B.A→C→F→B C.A→C→E→F→B D.A→C→M→B
B
3、如图点A、B表示两个居民小区,它们分别位于公路MN的两侧,现要在公路边建造一个车站C,使A、B两地居民小区的人乘车所走路程之和最短,那么车站应该建在什么地方?为什么?
A
B
M
N
对应练习
C
A
B
C
D
4、如图,有A、B、C、D四个村庄,这四个村庄要共建一个自来水塔,要求用水管最省.请问自来水塔应建在何处?
E
对应练习
对应练习
5、下列四个生活、生产现象:
① 用两个钉子就可以把木条固定在墙上;
② 植树时,只要定出两棵树的位置,就能确定同一行所在的直线;
③ 从A地到B地,架设电线,总是尽可能沿着线段AB架设;
④ 把弯曲的公路改直,就能缩短路程.其中可用定理“两点之间,线段最短”来解释的现象有 .(填序号)
①③
对应练习
6、平面上有 A,B 两点,且 AB=7cm.
(1) 若在该平面上找一点 C,使 CA+CB=7cm,则点 C 在何处?
(2) 若使 CA+CB>7cm,则点 C 在何处?
(3) 若使 CA+CB<7cm,存在这样的点C吗?
对应练习
7、已知点 B 在直线 AC 上,AB=4cm,AC=6cm,P,Q 分别是 AB,AC 的中点,求线段 PQ 的长.
对应练习
8、如图,B、C 两点把线段 MN 分成三部分,其比为 MB:BC:CN=2:3:4,点 P 是 MN 的中点,PC=2cm,求 MN 的长.
对应练习
9、如图,已知点 D 是线段 AB 上的一点,延长线段AB 至 C,使得 AB=BC,且 DC=5AD,若 BD=4cm,求线段 AC 的长.
对应练习
10、如图,已知线段 AB 和 CD 的公共部分 BD= AB= CD,线段 AB、CD 的中点 E、F 之间距离是 10cm,求AB,CD的长.
1
3
1
4
对应练习
11、线段 AB 上有两点 P,Q ,点 P 将 AB 分成两部分,AP:PB=2:3;点 Q 将 AB 也分成两部分,AQ:QB=4:1;且 PQ=3cm.求 AP,QB的长.
对应练习
12、如图,线段 AB=4,点 O 是线段 AB 上一点,C,D 分别是线段 OA,OB 的中点.
(1) 求线段 CD 的长.
(2) 若把“点O是线段AB上一点”改为“点O是线段AB延长线上一点”,其他条件不变,请你画出图形,并求出CD的长.
C
A
B
D
O
对应练习
13、 如图在数轴上有A,B两点,点A表示的数为-10,点O表示的数为0,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动,点N以每秒2个单位长度的速度从点O向右运动(点M,点N同时出发).
(1) 数轴上点B表示的数是 .
(2) 经过几秒,点M,N到原点的距离相等?
(3) 点N在点B左侧运动的情况下,当点M运动到什么位置时恰好使AM=2BN?
本节课你有什么收获?
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
