4.4.2角的度量单位与换算 课件(共29张PPT)
文档属性
| 名称 | 4.4.2角的度量单位与换算 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 456.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 13:23:52 | ||
图片预览



文档简介
(共29张PPT)
4.4.2 角的度量单位及换算
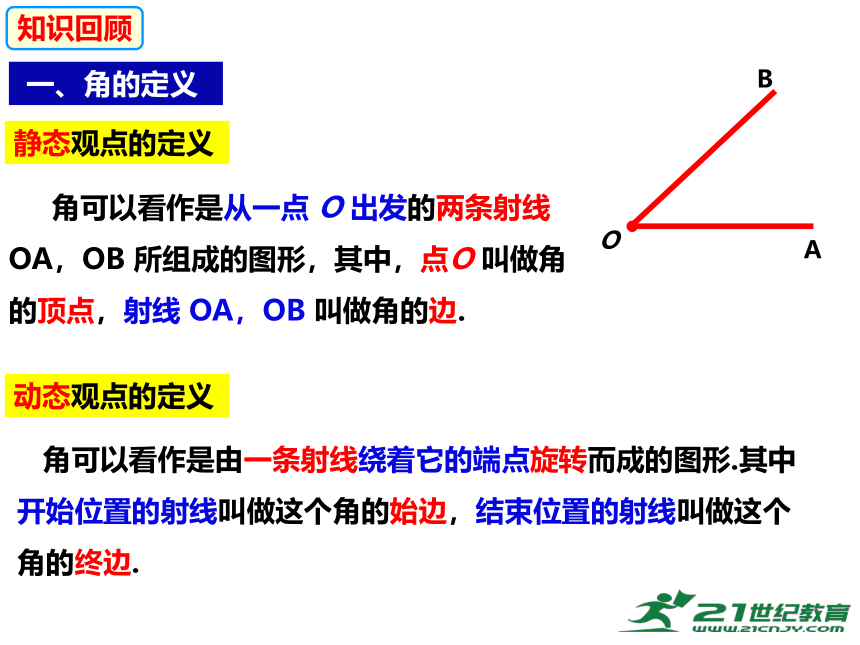
角可以看作是由一条射线绕着它的端点旋转而成的图形.其中开始位置的射线叫做这个角的始边,结束位置的射线叫做这个角的终边.
动态观点的定义
角可以看作是从一点 O 出发的两条射线 OA,OB 所组成的图形,其中,点O 叫做角的顶点,射线 OA,OB 叫做角的边.
O
A
B
静态观点的定义
一、角的定义
知识回顾
当以某一点为顶点的角只有一个时,
要把表示顶点的字母 O 写在中间,
要在角内部靠近顶点处加上弧线,并标上希腊字母.
A和B分别是角两边上的一点,写在两边,可以交换位置.
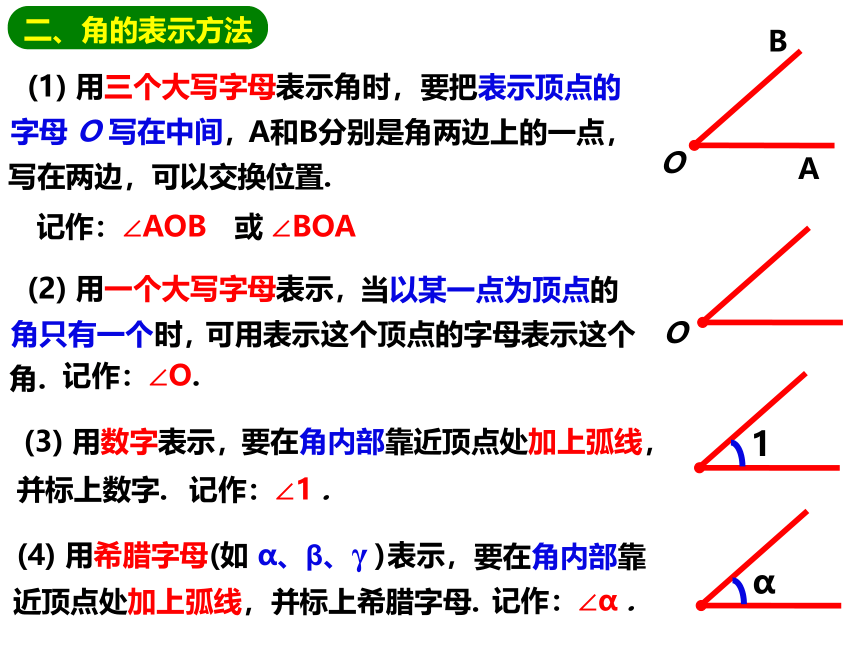
(1) 用三个大写字母表示角时,
O
A
B
记作:∠AOB
二、角的表示方法
或 ∠BOA
(2) 用一个大写字母表示,
O
(3) 用数字表示,
1
记作:∠1 .
可用表示这个顶点的字母表示这个角.
(4) 用希腊字母 表示,
α
记作:∠α .
记作:∠O.
并标上数字.
要在角内部靠近顶点处加上弧线,
(如 α、β、γ )
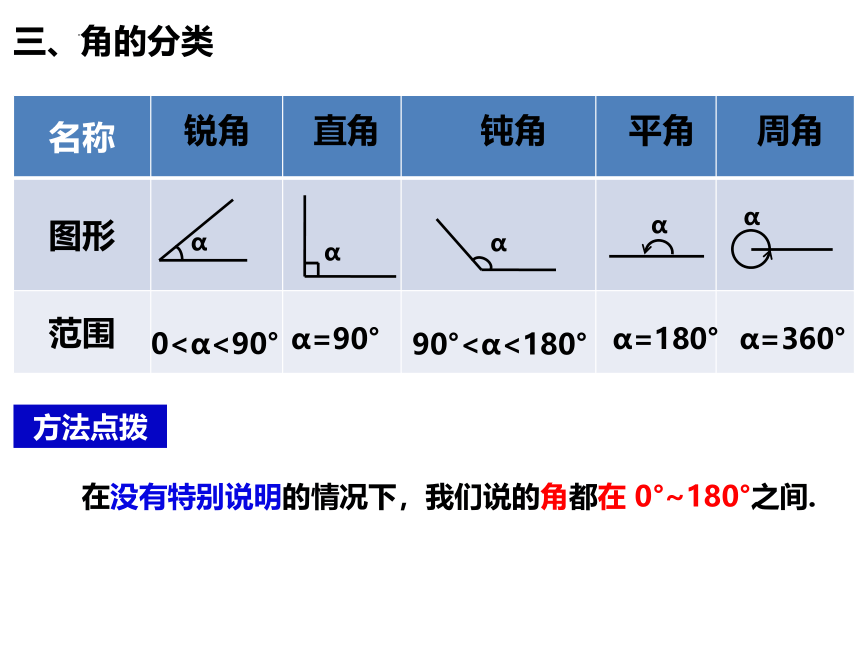
三、角的分类
名称
图形
范围
锐角
直角
钝角
平角
周角
α=360°
α=180°
α=90°
0<α<90°
90°<α<180°
α
α
α
α
α
方法点拨
在没有特别说明的情况下,我们说的角都在 0°~180°之间.
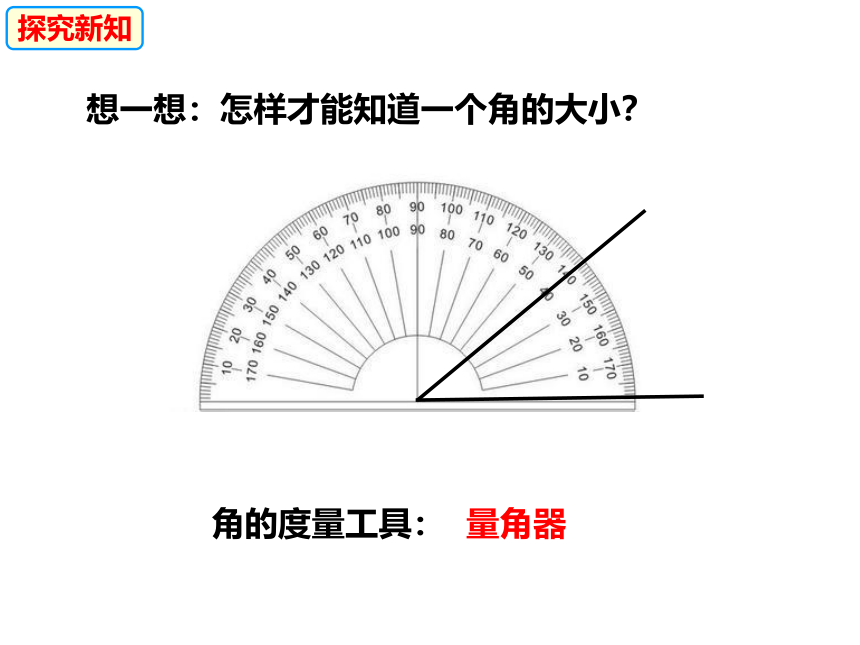
量角器
想一想:怎样才能知道一个角的大小?
角的度量工具:
探究新知
除了“度”之外,还有其它的度量单位吗?
角的度量单位:
把一个周角360等分,
记做 1°.
每一等份就是 1度 的角,
把1°的角60等分,
即 1°=
1分 记作 1′.
把1′的角60等分,
即 1′=
1秒 记作 1″.
度
、分
、秒
每一份就是 1分 的角,
每一份就是 1秒 的角,
或 1′=( )°
或 1″=
1度
1
60
60′
60″
( )′
1
60
方法点拨
角的度、分、秒
是 60 进制的,
这和钟表上的时、分、秒进制相同.
探究新知
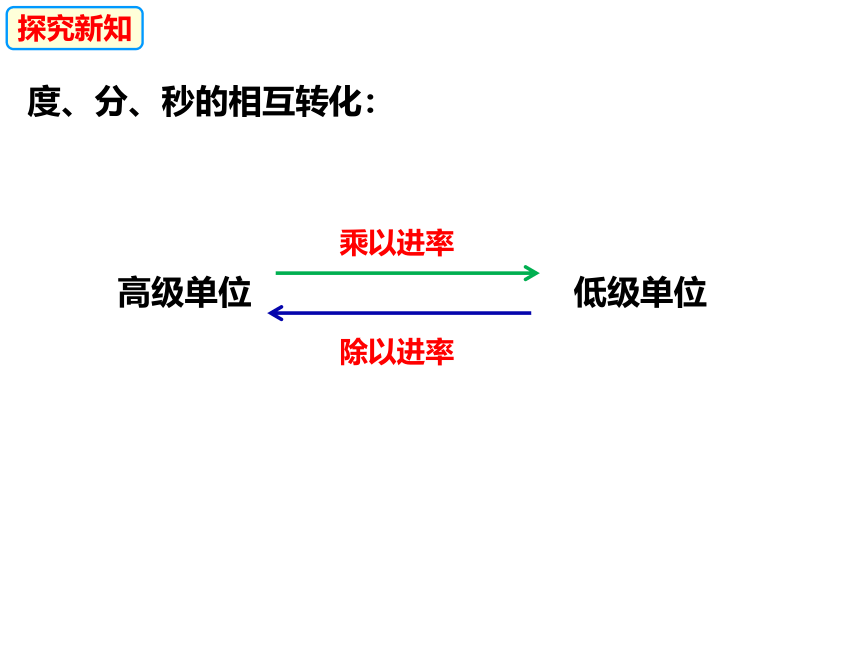
度、分、秒的相互转化:
高级单位
低级单位
乘以进率
除以进率
探究新知
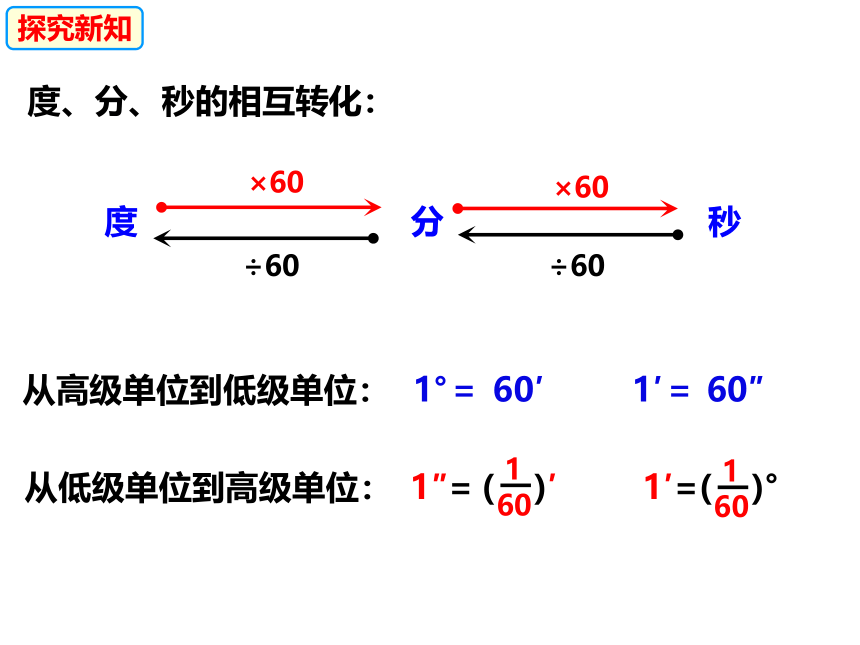
度、分、秒的相互转化:
度
分
÷60
秒
÷60
×60
×60
从高级单位到低级单位:
1°=
60′
1′=
60″
从低级单位到高级单位:
1″=
( )′
1
60
1′=( )°
1
60
要先把度的小数部分化成分,
例 1 角的度量单位的换算
(1) 用度、分、秒表示 30.26°;
解:
(1) 因为 0.26°=
0.6 ′=
所以 30.26°=
由度化为度、分、秒时,
再把分的小数部分化成秒.
0.26
=15.6 ′
0.6
=36 ″
30°15 ′36 ″.
方法点拨
从高级单位到低级单位:1°=60′,1′=60″.
×60′
×60 ″
因为 15"=
再把
(2) 42°18′15″等于多少度?
解:
18.25 ′=
所以 42°18′15″ ≈ 42.304°.
要先把秒化成分,
由度、分、秒化为度时,
例 1 角的度量单位的换算
18.25
15
×
= 0.25′
×( )°
≈ 0.304°
1
60
方法点拨
分化成度.
从低级单位到高级单位:
1″=
( )′
1
60
1′=( )°
1
60
对应练习
1、填空:
(1) 53.37° = ° ′ ″
53
22
12
(2) 24°12′36″= °
24.21
2、1.45°等于多少分?等于多少秒?
对应练习
解:1.45°=
1.45°=
1.45×60'
=87'
87'
=87×60''
=5220''
(1) 25°23′17″+46°53′43″
解:
= 72°17′
例 2 度、分、秒的加、减法运算
原式= 71°76′60″
(2) 75°23′12″ - 46°53′43″
解:
= 28°29′29″
原式= 74°82′72″-46°53′43″
在进行角的度数加、减法的运算时,本着“度与度加减、分与分加减、秒与秒加减”的原则进行,如果不够减时向前借1当60,相加时,满60向前进1.
方法点拨
例 2 度、分、秒的加、减法运算
(3) 90°-37°24′38″
对应练习
= 52°35′22″
解:
原式=
89°59′60″-37°24′38″
例 2 度、分、秒的加、减法运算
解:
原式=
265°125′140″
=267°7′20″
例 3 度、分、秒的乘法运算
53°25′28″×5
方法点拨
然后把分、秒逢60进1位即可.
度数乘以一个数,
先让度、分、秒分别乘以这个数,
例 4 度、分、秒的除法运算
(1) 15°20′ ÷ 6
2°+3°20′÷6
解:
原式=
=2°+200′÷6
=2°+30′+20'÷6
=2°+30′+120”÷6
=2°+30′+20”
方法点拨
=2°30′20”
再将余数化为秒,加到秒位上,用秒位再除以这个数.
把余数乘60化成分,
度数除以一个数,
先用度除以这个数,
加到分位上,
再用分位除以这个数,
解:
原式=
44°+2°22′ ÷ 3
= 44°+142′÷ 3
≈ 44°+47′
(精确到1')
=44°47′
例 4 度、分、秒的除法运算
(2) 134°22′÷3
1、计算
对应练习
(2) 90°-68°17′50″
(3) 52°22′×9
(4) 178°53′÷ 5
(精确到 1′)
(1) 30°19′21″+15°40′42″
2、若 ∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )
对应练习
A. ∠A>∠B>∠C
B. ∠B>∠A>∠C
C. ∠A>∠C>∠B
B. ∠C>∠A>∠B
C
1、如图是中央电视台部分节目的播出时间,分别确定钟表上时针与分针所成的最小角的度数.
巩固练习
每一大格所对角的度数为 30°,
方法点拨
每一小格所对角的度数为 6°.
钟面表盘被平均分成 12 大格,
150°
0°
分针 5min 旋转的角度是 .一天 24h 中时钟的分针和时针组成 次平角, 次周角.
2、小红早晨 8:30 出发,中午 12:30 到家,则小红出发时时针和分针的夹角为 ,到家时时针和分针的夹角为 .
75°
165°
巩固练习
变式练习:
30°
24
24
3、(1) 1点10分时,时钟的时针与分针的夹角是几度?2 点25分时,时钟的时针与分针的夹角又是几度?
巩固练习
① 时针:
方法点拨
每小时转
=30°,
每分钟转
= 0.5°
360°
12
30°
60
② 分针:
每小时转
360°,
每分钟转
= 6°
360°
60
3、 (2) 从1点15分到1点35分,时钟的时针与分针各转了多大角度?
巩固练习
① 时针:
方法点拨
每小时转
=30°,
每分钟转
= 0.5°
360°
12
30°
60
② 分针:
每小时转
360°,
每分钟转
= 6°
360°
60
巩固练习
4、平时测量时,通常以正北、正南方向为基准,描述物体运动的方向,这种表示方向的角叫做方向角,在测绘、航海中经常用到.如图,OA 是表示北偏东 20° 方向的一条射线.仿照画出下列方向的射线:
(1) 北偏西50°;
(2) 南偏东10°;
(3) 西南方向(即南偏西45°)
5、已知一条射线 OA,若从点 O 再引两条射线 OB,OC,使 ∠AOB=72°,∠BOC=36°,求∠AOC的度数.
巩固练习
6、从 6 时到 7 时,这 1 个小时内钟表表面的时针与分针何时的夹角为 60°?
巩固练习
本节课你有什么收获?
角的度量单位:
度
、分
、秒
度
分
÷60
秒
÷60
×60
×60
从高级单位到低级单位:
1°=
60′
1′=
60″
从低级单位到高级单位:
1″=
( )′
1
60
1′=( )°
1
60
4.4.2 角的度量单位及换算
角可以看作是由一条射线绕着它的端点旋转而成的图形.其中开始位置的射线叫做这个角的始边,结束位置的射线叫做这个角的终边.
动态观点的定义
角可以看作是从一点 O 出发的两条射线 OA,OB 所组成的图形,其中,点O 叫做角的顶点,射线 OA,OB 叫做角的边.
O
A
B
静态观点的定义
一、角的定义
知识回顾
当以某一点为顶点的角只有一个时,
要把表示顶点的字母 O 写在中间,
要在角内部靠近顶点处加上弧线,并标上希腊字母.
A和B分别是角两边上的一点,写在两边,可以交换位置.
(1) 用三个大写字母表示角时,
O
A
B
记作:∠AOB
二、角的表示方法
或 ∠BOA
(2) 用一个大写字母表示,
O
(3) 用数字表示,
1
记作:∠1 .
可用表示这个顶点的字母表示这个角.
(4) 用希腊字母 表示,
α
记作:∠α .
记作:∠O.
并标上数字.
要在角内部靠近顶点处加上弧线,
(如 α、β、γ )
三、角的分类
名称
图形
范围
锐角
直角
钝角
平角
周角
α=360°
α=180°
α=90°
0<α<90°
90°<α<180°
α
α
α
α
α
方法点拨
在没有特别说明的情况下,我们说的角都在 0°~180°之间.
量角器
想一想:怎样才能知道一个角的大小?
角的度量工具:
探究新知
除了“度”之外,还有其它的度量单位吗?
角的度量单位:
把一个周角360等分,
记做 1°.
每一等份就是 1度 的角,
把1°的角60等分,
即 1°=
1分 记作 1′.
把1′的角60等分,
即 1′=
1秒 记作 1″.
度
、分
、秒
每一份就是 1分 的角,
每一份就是 1秒 的角,
或 1′=( )°
或 1″=
1度
1
60
60′
60″
( )′
1
60
方法点拨
角的度、分、秒
是 60 进制的,
这和钟表上的时、分、秒进制相同.
探究新知
度、分、秒的相互转化:
高级单位
低级单位
乘以进率
除以进率
探究新知
度、分、秒的相互转化:
度
分
÷60
秒
÷60
×60
×60
从高级单位到低级单位:
1°=
60′
1′=
60″
从低级单位到高级单位:
1″=
( )′
1
60
1′=( )°
1
60
要先把度的小数部分化成分,
例 1 角的度量单位的换算
(1) 用度、分、秒表示 30.26°;
解:
(1) 因为 0.26°=
0.6 ′=
所以 30.26°=
由度化为度、分、秒时,
再把分的小数部分化成秒.
0.26
=15.6 ′
0.6
=36 ″
30°15 ′36 ″.
方法点拨
从高级单位到低级单位:1°=60′,1′=60″.
×60′
×60 ″
因为 15"=
再把
(2) 42°18′15″等于多少度?
解:
18.25 ′=
所以 42°18′15″ ≈ 42.304°.
要先把秒化成分,
由度、分、秒化为度时,
例 1 角的度量单位的换算
18.25
15
×
= 0.25′
×( )°
≈ 0.304°
1
60
方法点拨
分化成度.
从低级单位到高级单位:
1″=
( )′
1
60
1′=( )°
1
60
对应练习
1、填空:
(1) 53.37° = ° ′ ″
53
22
12
(2) 24°12′36″= °
24.21
2、1.45°等于多少分?等于多少秒?
对应练习
解:1.45°=
1.45°=
1.45×60'
=87'
87'
=87×60''
=5220''
(1) 25°23′17″+46°53′43″
解:
= 72°17′
例 2 度、分、秒的加、减法运算
原式= 71°76′60″
(2) 75°23′12″ - 46°53′43″
解:
= 28°29′29″
原式= 74°82′72″-46°53′43″
在进行角的度数加、减法的运算时,本着“度与度加减、分与分加减、秒与秒加减”的原则进行,如果不够减时向前借1当60,相加时,满60向前进1.
方法点拨
例 2 度、分、秒的加、减法运算
(3) 90°-37°24′38″
对应练习
= 52°35′22″
解:
原式=
89°59′60″-37°24′38″
例 2 度、分、秒的加、减法运算
解:
原式=
265°125′140″
=267°7′20″
例 3 度、分、秒的乘法运算
53°25′28″×5
方法点拨
然后把分、秒逢60进1位即可.
度数乘以一个数,
先让度、分、秒分别乘以这个数,
例 4 度、分、秒的除法运算
(1) 15°20′ ÷ 6
2°+3°20′÷6
解:
原式=
=2°+200′÷6
=2°+30′+20'÷6
=2°+30′+120”÷6
=2°+30′+20”
方法点拨
=2°30′20”
再将余数化为秒,加到秒位上,用秒位再除以这个数.
把余数乘60化成分,
度数除以一个数,
先用度除以这个数,
加到分位上,
再用分位除以这个数,
解:
原式=
44°+2°22′ ÷ 3
= 44°+142′÷ 3
≈ 44°+47′
(精确到1')
=44°47′
例 4 度、分、秒的除法运算
(2) 134°22′÷3
1、计算
对应练习
(2) 90°-68°17′50″
(3) 52°22′×9
(4) 178°53′÷ 5
(精确到 1′)
(1) 30°19′21″+15°40′42″
2、若 ∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )
对应练习
A. ∠A>∠B>∠C
B. ∠B>∠A>∠C
C. ∠A>∠C>∠B
B. ∠C>∠A>∠B
C
1、如图是中央电视台部分节目的播出时间,分别确定钟表上时针与分针所成的最小角的度数.
巩固练习
每一大格所对角的度数为 30°,
方法点拨
每一小格所对角的度数为 6°.
钟面表盘被平均分成 12 大格,
150°
0°
分针 5min 旋转的角度是 .一天 24h 中时钟的分针和时针组成 次平角, 次周角.
2、小红早晨 8:30 出发,中午 12:30 到家,则小红出发时时针和分针的夹角为 ,到家时时针和分针的夹角为 .
75°
165°
巩固练习
变式练习:
30°
24
24
3、(1) 1点10分时,时钟的时针与分针的夹角是几度?2 点25分时,时钟的时针与分针的夹角又是几度?
巩固练习
① 时针:
方法点拨
每小时转
=30°,
每分钟转
= 0.5°
360°
12
30°
60
② 分针:
每小时转
360°,
每分钟转
= 6°
360°
60
3、 (2) 从1点15分到1点35分,时钟的时针与分针各转了多大角度?
巩固练习
① 时针:
方法点拨
每小时转
=30°,
每分钟转
= 0.5°
360°
12
30°
60
② 分针:
每小时转
360°,
每分钟转
= 6°
360°
60
巩固练习
4、平时测量时,通常以正北、正南方向为基准,描述物体运动的方向,这种表示方向的角叫做方向角,在测绘、航海中经常用到.如图,OA 是表示北偏东 20° 方向的一条射线.仿照画出下列方向的射线:
(1) 北偏西50°;
(2) 南偏东10°;
(3) 西南方向(即南偏西45°)
5、已知一条射线 OA,若从点 O 再引两条射线 OB,OC,使 ∠AOB=72°,∠BOC=36°,求∠AOC的度数.
巩固练习
6、从 6 时到 7 时,这 1 个小时内钟表表面的时针与分针何时的夹角为 60°?
巩固练习
本节课你有什么收获?
角的度量单位:
度
、分
、秒
度
分
÷60
秒
÷60
×60
×60
从高级单位到低级单位:
1°=
60′
1′=
60″
从低级单位到高级单位:
1″=
( )′
1
60
1′=( )°
1
60
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
