5.5 应用二元一次方程组-里程碑上的数 课件(共25张PPT)
文档属性
| 名称 | 5.5 应用二元一次方程组-里程碑上的数 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 07:19:34 | ||
图片预览







文档简介
(共25张PPT)
第五章 二元一次方程组
5.5应用二元一次方程组--里程碑上的数
北师版 数学 八年级上册
学习目标
1.利用二元一次方程解决数字问题和行程问题。
2.进一步经历和体验列方程组解决实际问题的过程。
3.能分析复杂问题中的数量关系,建立方程组解决问题。
情景导入
悟空顺风探妖踪,千里只行四分钟.
归时四分行六百,风速多少才称雄?
探索新知
利用二元一次方程组解决数字问题
一
小结:多位数表示方法就是在每个数位上的数字乘对应
的数位单位再相加.
理解如何把多位数用代数式表示?
如:523
百
十
个
百
十
个
5×100 + 2×10 + 3
可以写成代数式
探索新知
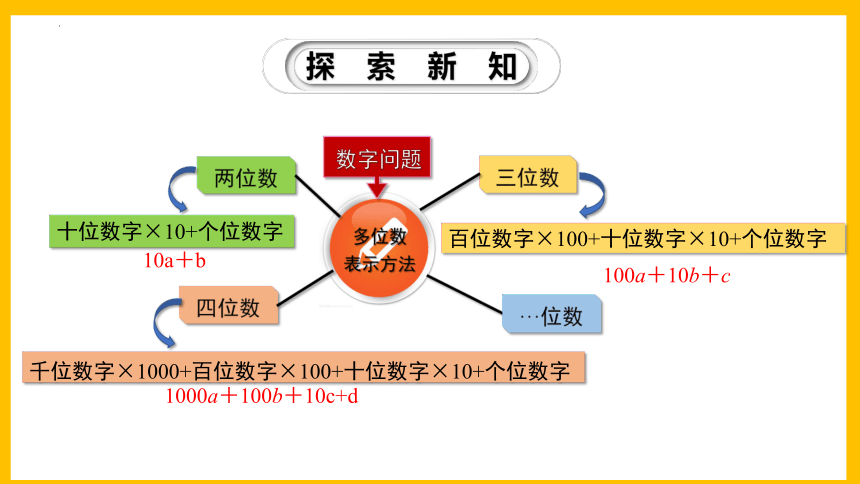
多位数
表示方法
两位数
百位数字×100+十位数字×10+个位数字
千位数字×1000+百位数字×100+十位数字×10+个位数字
十位数字×10+个位数字
三位数
四位数
···位数
10a+b
100a+10b+c
1000a+100b+10c+d
数字问题
探索新知
一个最小的两位自然数等于它的十位数字与个位数字的和的3倍,那么这个两位数是多少?
∵ 10x+y=3(x+y),
∴7x=2y,
∵此数是一个最小的两位自然数,
∴x=2,y=7,
∴这个两位数是27.
解:设十位数字为x,个位数字为y.
探索新知
是一个两位数字,
它的两个数字之和为7.
12:00
13:00
14:00
十位与个位数字与12:00时所看到的正好颠倒了.
比12:00时看到的两位数中间多了个0.
例1 小明爸爸骑着摩托车带着小明在公路上匀速行驶,下图是小明每隔1小时看到的里程情况.你能确定小明在12:00时看到的里程碑上的数吗?
探索新知
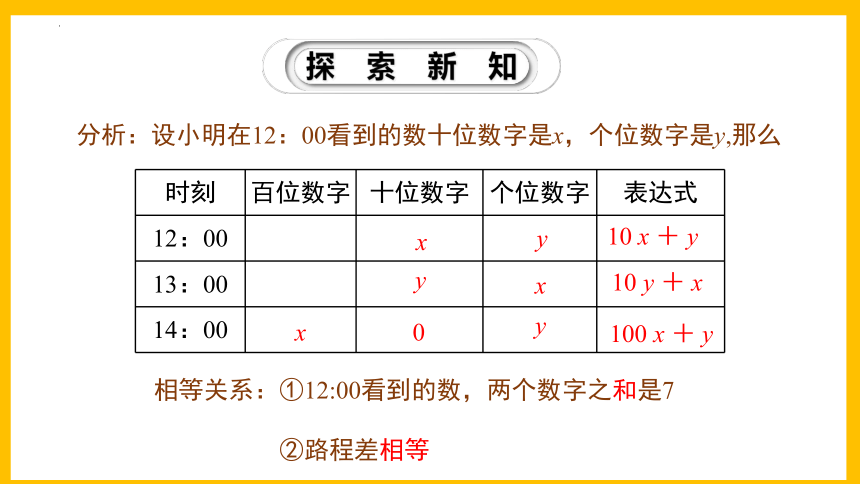
分析:设小明在12:00看到的数十位数字是x,个位数字是y,那么
时刻 百位数字 十位数字 个位数字 表达式
12:00
13:00
14:00
x
y
y
x
10 y + x
x
0
y
100 x + y
相等关系:①12:00看到的数,两个数字之和是7
②路程差相等
10 x + y
探索新知
解:如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么根据以上分析,得方程组:
解得
答:小明在12:00时看到的里程碑上的数是16.
整理得
探索新知
例2:两个两位数的和为 68,在较大的两位数的右边接着写较小的两位数,得到一个四位数; 在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大2178, 求这两个两位数.
分析:设较大的两位数为x,较小的两位数为y,则
两个两位数 左边 右边 表达式
大左小右
小左大右
较大x
较小y
较小y
较大x
100 y + x
10 0x + y
探索新知
解:设较大的两位数为x,较小的两位数为y,则
解方程组,得:
答:这两个两位数分别是45和23.
x+y=68
(100x+y)-(100y+x)=2178
x=45
y=23
总结归纳
探索新知
求两位数或三位数时
不能直接
设这个两位数或
三位数的
把各个数位上的数字
设为未知数
弄清题意
解题的关键
找出等量关系
列出方程组
求解
探索新知
利用二元一次方程组解决行程问题
二
例3 小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路走平均速度60m/min,下坡路平均速度80m/min,上坡路平均速度40m/min,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
探索新知
方法1:直接设元法
分析:设小华家到学校平路长x m,下坡长y m.
平路时间 坡路时间 总时间
上学
放学
平路:60m/min
下坡路:80m/min
上坡路:40m/min
探索新知
解:设小华家到学校平路长x m,下坡长y m.
根据题意,可列方程组:
解方程组,得
答:小明家到学校的距离为700米.
方法1:直接设元法
探索新知
方法2:间接设元法
平路:60m/min
下坡路:80m/min
上坡路:40m/min
分析:设小华下坡路所花时间为x min,
上坡路所花时间为y min.
平路距离 坡路距离
上学
放学
探索新知
方法12:间接设元法
解:设小华下坡路所花时间为xmin,上坡路所花时间为ymin.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
故平路距离:60×(10-5)=300(米)
坡路距离:80×5=400(米)
当堂检测
C
当堂检测
B
当堂检测
3.甲、乙两地相距20千米,小明从甲地向乙地前进,同时,小亮从乙地向甲地前进,2小时相遇.相遇后,小明返回甲地,小亮继续向甲地前进,小明回到甲地时,小亮离甲地还有2千米.若两人都是匀速前进的,则小明、小亮的速度分别为( )
A.4.5千米/时,4.5千米/时
B.3.5千米/时,4.5千米/时
C.5.5千米/时,3.5千米/时
D.5.5千米/时,4.5千米/时
D
当堂检测
4.甲、乙两地相距100千米,一艘轮船往返两地顺流用4小时,逆流用5小时,那么这艘轮船在静水中的速度是_______千米/时,水流速度是______千米/时.
22.5
2.5
5.小华4年后的年龄与小丽4年前的年龄相等,3年后她们两人的年龄和等于她们今年年龄差的3倍.则小华和小丽今年的年龄分别是_________________.
5岁、13岁
当堂检测
当堂检测
当堂检测
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程或方程组的方法来处理这些问题.
2.这种处理问题的过程可以进一步概括为:
3.要注意的是,处理实际问题的方法是多种多样的,图表分析是一种直观简洁的方法,设间接未知数可帮助转化问题,还可运用化归等数学思想方法,应根据具体问题灵活选用.
问题 方程(组) 解答
抽象 检验
分析 求解
第五章 二元一次方程组
5.5应用二元一次方程组--里程碑上的数
北师版 数学 八年级上册
学习目标
1.利用二元一次方程解决数字问题和行程问题。
2.进一步经历和体验列方程组解决实际问题的过程。
3.能分析复杂问题中的数量关系,建立方程组解决问题。
情景导入
悟空顺风探妖踪,千里只行四分钟.
归时四分行六百,风速多少才称雄?
探索新知
利用二元一次方程组解决数字问题
一
小结:多位数表示方法就是在每个数位上的数字乘对应
的数位单位再相加.
理解如何把多位数用代数式表示?
如:523
百
十
个
百
十
个
5×100 + 2×10 + 3
可以写成代数式
探索新知
多位数
表示方法
两位数
百位数字×100+十位数字×10+个位数字
千位数字×1000+百位数字×100+十位数字×10+个位数字
十位数字×10+个位数字
三位数
四位数
···位数
10a+b
100a+10b+c
1000a+100b+10c+d
数字问题
探索新知
一个最小的两位自然数等于它的十位数字与个位数字的和的3倍,那么这个两位数是多少?
∵ 10x+y=3(x+y),
∴7x=2y,
∵此数是一个最小的两位自然数,
∴x=2,y=7,
∴这个两位数是27.
解:设十位数字为x,个位数字为y.
探索新知
是一个两位数字,
它的两个数字之和为7.
12:00
13:00
14:00
十位与个位数字与12:00时所看到的正好颠倒了.
比12:00时看到的两位数中间多了个0.
例1 小明爸爸骑着摩托车带着小明在公路上匀速行驶,下图是小明每隔1小时看到的里程情况.你能确定小明在12:00时看到的里程碑上的数吗?
探索新知
分析:设小明在12:00看到的数十位数字是x,个位数字是y,那么
时刻 百位数字 十位数字 个位数字 表达式
12:00
13:00
14:00
x
y
y
x
10 y + x
x
0
y
100 x + y
相等关系:①12:00看到的数,两个数字之和是7
②路程差相等
10 x + y
探索新知
解:如果设小明在12:00时看到的数的十位数字是x,个位数字是y,那么根据以上分析,得方程组:
解得
答:小明在12:00时看到的里程碑上的数是16.
整理得
探索新知
例2:两个两位数的和为 68,在较大的两位数的右边接着写较小的两位数,得到一个四位数; 在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大2178, 求这两个两位数.
分析:设较大的两位数为x,较小的两位数为y,则
两个两位数 左边 右边 表达式
大左小右
小左大右
较大x
较小y
较小y
较大x
100 y + x
10 0x + y
探索新知
解:设较大的两位数为x,较小的两位数为y,则
解方程组,得:
答:这两个两位数分别是45和23.
x+y=68
(100x+y)-(100y+x)=2178
x=45
y=23
总结归纳
探索新知
求两位数或三位数时
不能直接
设这个两位数或
三位数的
把各个数位上的数字
设为未知数
弄清题意
解题的关键
找出等量关系
列出方程组
求解
探索新知
利用二元一次方程组解决行程问题
二
例3 小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路走平均速度60m/min,下坡路平均速度80m/min,上坡路平均速度40m/min,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
探索新知
方法1:直接设元法
分析:设小华家到学校平路长x m,下坡长y m.
平路时间 坡路时间 总时间
上学
放学
平路:60m/min
下坡路:80m/min
上坡路:40m/min
探索新知
解:设小华家到学校平路长x m,下坡长y m.
根据题意,可列方程组:
解方程组,得
答:小明家到学校的距离为700米.
方法1:直接设元法
探索新知
方法2:间接设元法
平路:60m/min
下坡路:80m/min
上坡路:40m/min
分析:设小华下坡路所花时间为x min,
上坡路所花时间为y min.
平路距离 坡路距离
上学
放学
探索新知
方法12:间接设元法
解:设小华下坡路所花时间为xmin,上坡路所花时间为ymin.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
故平路距离:60×(10-5)=300(米)
坡路距离:80×5=400(米)
当堂检测
C
当堂检测
B
当堂检测
3.甲、乙两地相距20千米,小明从甲地向乙地前进,同时,小亮从乙地向甲地前进,2小时相遇.相遇后,小明返回甲地,小亮继续向甲地前进,小明回到甲地时,小亮离甲地还有2千米.若两人都是匀速前进的,则小明、小亮的速度分别为( )
A.4.5千米/时,4.5千米/时
B.3.5千米/时,4.5千米/时
C.5.5千米/时,3.5千米/时
D.5.5千米/时,4.5千米/时
D
当堂检测
4.甲、乙两地相距100千米,一艘轮船往返两地顺流用4小时,逆流用5小时,那么这艘轮船在静水中的速度是_______千米/时,水流速度是______千米/时.
22.5
2.5
5.小华4年后的年龄与小丽4年前的年龄相等,3年后她们两人的年龄和等于她们今年年龄差的3倍.则小华和小丽今年的年龄分别是_________________.
5岁、13岁
当堂检测
当堂检测
当堂检测
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程或方程组的方法来处理这些问题.
2.这种处理问题的过程可以进一步概括为:
3.要注意的是,处理实际问题的方法是多种多样的,图表分析是一种直观简洁的方法,设间接未知数可帮助转化问题,还可运用化归等数学思想方法,应根据具体问题灵活选用.
问题 方程(组) 解答
抽象 检验
分析 求解
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
