28.2.2 解直角三角形的应用(1)(课件)(共24张PPT)
文档属性
| 名称 | 28.2.2 解直角三角形的应用(1)(课件)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
解直角三角形的应用(1)
1.巩固解直角三角形有关知识; (重点)
2.能运用解直角三角形知识解决仰角和俯角有关的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路. (重点、难点)
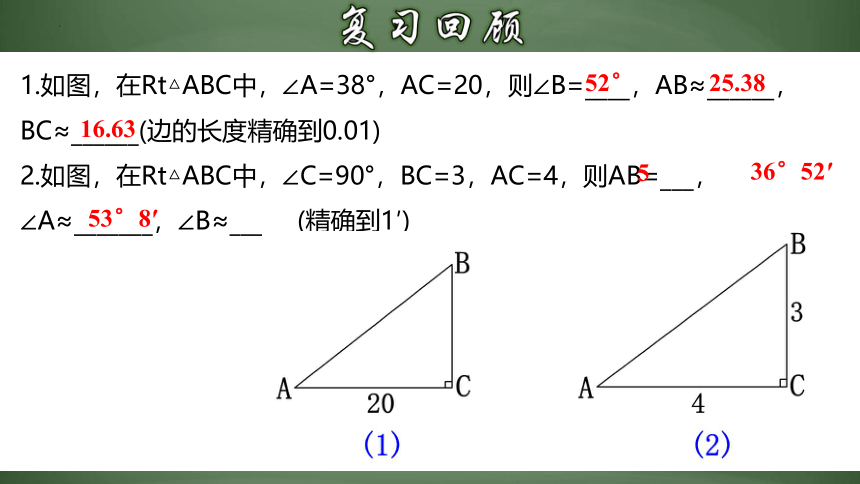
1.如图,在Rt△ABC中,∠A=38°,AC=20,则∠B=____,AB≈______,BC≈______(边的长度精确到0.01)
2.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则AB=___,∠A≈_______,∠B≈______(精确到1′)
52°
25.38
16.63
5
36°52′
53°8′
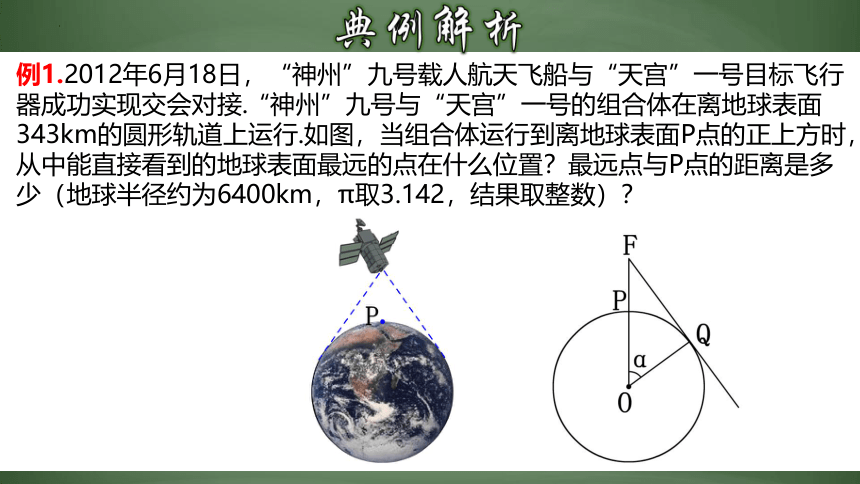
例1.2012年6月18日,“神州”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.“神州”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行.如图,当组合体运行到离地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P点的距离是多少(地球半径约为6400km,π取3.142,结果取整数)?
解:设∠POQ=α,在右图中,FQ是⊙O的切线,△FOQ是
直角三角形.
∵ cosα= = ≈0.9491
∴ α≈18.36°
∴ 的长为 (km)
由此可知,当组合体在P点正上方时,从中观测地球表面时的最远点距离P点约2051km.
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
2.根据条件的特点,适当选用锐角三角函数去解直角三角形;
画出平面图形,转化为解直角三角形的问题
3.得到数学问题的答案;
4.得到实际问题的答案.
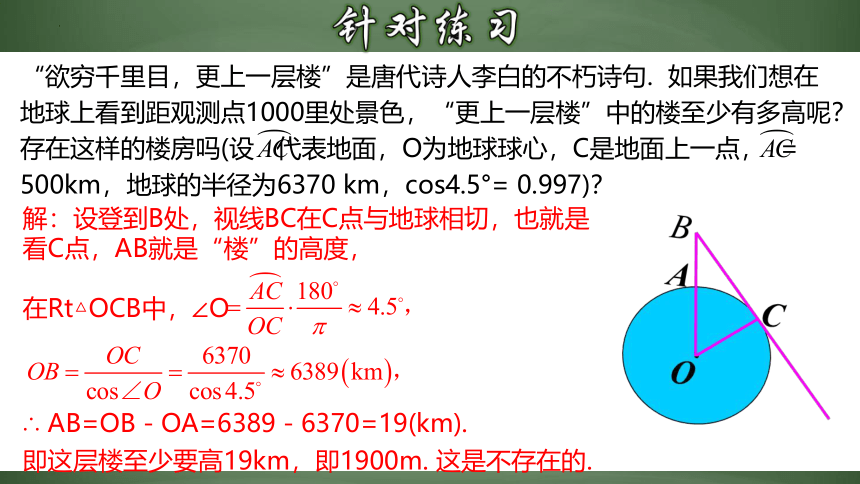
“欲穷千里目,更上一层楼”是唐代诗人李白的不朽诗句. 如果我们想在地球上看到距观测点1000里处景色,“更上一层楼”中的楼至少有多高呢?存在这样的楼房吗(设 代表地面,O为地球球心,C是地面上一点, =
500km,地球的半径为6370 km,cos4.5°= 0.997)?
解:设登到B处,视线BC在C点与地球相切,也就是
看C点,AB就是“楼”的高度,
∴ AB=OB-OA=6389-6370=19(km).
即这层楼至少要高19km,即1900m. 这是不存在的.
在Rt△OCB中,∠O
例2.热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,这栋楼有多高(结果取整数)?
在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
解:如图,α=30,β=60°,AD=120.
∵ tanα= ,tanβ=
∴ BD=AD tanα=120×tan30°=120× =40
CD=AD tanβ=120×tan60°=120×=120
∴ BC=BD+CD=40+120=160≈277(m)
因此,这栋楼高约为277m.
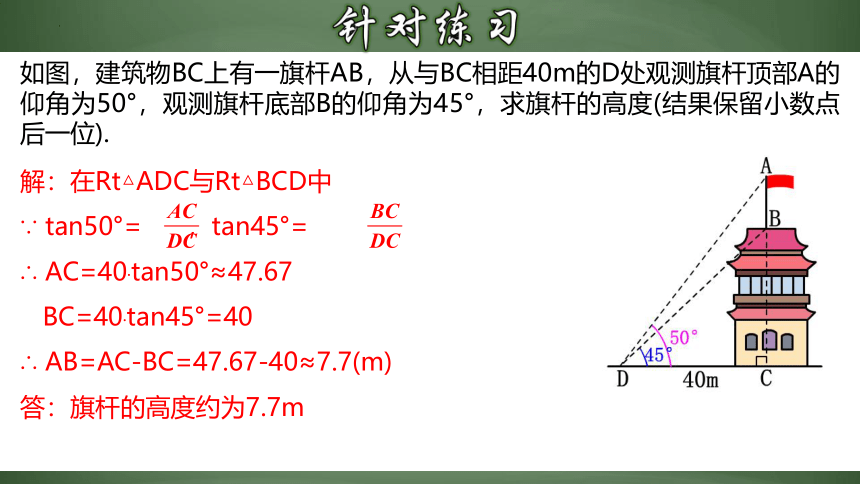
如图,建筑物BC上有一旗杆AB,从与BC相距40m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,求旗杆的高度(结果保留小数点后一位).
解:在Rt△ADC与Rt△BCD中
∵ tan50°= ,tan45°=
∴ AC=40·tan50°≈47.67
BC=40·tan45°=40
∴ AB=AC-BC=47.67-40≈7.7(m)
答:旗杆的高度约为7.7m
例3.如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为30°,已知AB=6m,DE=10m,求乙楼AC的高度(参考数据: ≈1.41,≈1.73,精确到0. 1m).
解:如图,过点E作EF⊥AC于F,则四边形CDEF为矩形.
∴EF=CD,CF=DE=1Om
由题意得∠DAC=∠ADC=45°,∠BEF=30°
设AC=xm,则CD=EF=xm,BF=AC-CF-AB=(x-16)m
在Rt△BEF中,tan∠BEF=
即 ,解得x≈37.8(m)
答:乙楼AC的高度约为37.8m
如图,在数学活动课上,某学习小组在校园内用测量仪测量一棵树的高度,在C处测得,在E处测得,米,仪器高度米,请根据测量的数据计算这棵树的高度(结果精确到0.1米).(参考数据:,,,,,)
解:延长交于H,则易知,
设(米),
,
,
在中,,
,
在中,,
如图,在数学活动课上,某学习小组在校园内用测量仪测量一棵树的高度,在C处测得,在E处测得,米,仪器高度米,请根据测量的数据计算这棵树的高度(结果精确到0.1米).(参考数据:,,,,,)
,
,
即(米);
又,
四边形为矩形,
(米)
答:这棵树AB的高度为米.
1.从一艘船上测得海岸_上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米 B.14米 C.21米 D.42米.
2.身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
A.甲 B.乙 C.丙 D.丁
A
D
3.如图,某航天飞船在地球表面点P的正上方A处,从A处观测到地球表面的最远点Q,若∠QAP=a,地球半径为R,则航天飞船距离地球表面的最近距离AP以及P,Q两点间的地面距离分别是( )
A. B.
C. D.
B
4.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BC0=x,则点A到OC的距离等于( )
A. a·sinx+b·sinx
B. a·cosx+b·cosx
C. a·sinx+b·cosx
D. a·cosx+b·sinx
D
5.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为
_________m.(结果保留根号)
6.如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为______米. (结果保留根号)
5+5
1
7.某公共场所准备改善原有楼梯的安全性能,把倾角由45°减至30°,楼梯高度不变.已知楼梯原长4m,那么调整的楼梯.会增加多长 楼梯多占了多长一段地面
解:在Rt△ABC中,AB=4,∠ABC=45°
∴BC=AC=AB·sin45°=2m
在Rt△ADC中,AC=2,∠ADC=30°
∴AD= m,DC= m
∴AD-AB=(4-4)m,DC-BC=(2-2)m
答:调整后楼梯会增加(4-4)m,占地会加长(2-2)m.
8.如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m)
解:在Rt△ACD中,∠A=30°
∴tan30 °= ∴AC=CD
在Rt△BCD中,∠CBD=60°
∴tan60°= ,∴BC=CD
∵AC-BC=50,∴CD-CD=50 解得,CD≈43
答:该塔约为43m高.
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
解:由题意得,,
则四边形均为矩形.
所以米,米,
在中,,则.设米,
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
在中,,
则,即,
解得:,
所以米,
则(米).
答:八仙阁AB的高度为48米.
10.如图,某学习小组在学习了“利用三角函数测高后”,选定测量小河对面一幢建筑物的高度.他们先在斜坡的D处,测得建筑物顶端B的仰角为,且D离地面的高度为9米,坡底的长度米,然后在A处测得建筑物顶端B的仰角为,点E,A,C在同一水平线上,求建筑物的高度.(结果精确到1米,参考数据:)
解:过点作,交于点.
∵,,,
∴四边形为矩形,
∴,米,
又∵,,
∴,
10.如图,某学习小组在学习了“利用三角函数测高后”,选定测量小河对面一幢建筑物的高度.他们先在斜坡的D处,测得建筑物顶端B的仰角为,且D离地面的高度为9米,坡底的长度米,然后在A处测得建筑物顶端B的仰角为,点E,A,C在同一水平线上,求建筑物的高度.(结果精确到1米,参考数据:)
∴,
又∵,
∴,
即,
∴米.
解直角三角形的应用(1)
1.巩固解直角三角形有关知识; (重点)
2.能运用解直角三角形知识解决仰角和俯角有关的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路. (重点、难点)
1.如图,在Rt△ABC中,∠A=38°,AC=20,则∠B=____,AB≈______,BC≈______(边的长度精确到0.01)
2.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则AB=___,∠A≈_______,∠B≈______(精确到1′)
52°
25.38
16.63
5
36°52′
53°8′
例1.2012年6月18日,“神州”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.“神州”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行.如图,当组合体运行到离地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P点的距离是多少(地球半径约为6400km,π取3.142,结果取整数)?
解:设∠POQ=α,在右图中,FQ是⊙O的切线,△FOQ是
直角三角形.
∵ cosα= = ≈0.9491
∴ α≈18.36°
∴ 的长为 (km)
由此可知,当组合体在P点正上方时,从中观测地球表面时的最远点距离P点约2051km.
利用解直角三角形解决实际问题的一般过程:
1.将实际问题抽象为数学问题;
2.根据条件的特点,适当选用锐角三角函数去解直角三角形;
画出平面图形,转化为解直角三角形的问题
3.得到数学问题的答案;
4.得到实际问题的答案.
“欲穷千里目,更上一层楼”是唐代诗人李白的不朽诗句. 如果我们想在地球上看到距观测点1000里处景色,“更上一层楼”中的楼至少有多高呢?存在这样的楼房吗(设 代表地面,O为地球球心,C是地面上一点, =
500km,地球的半径为6370 km,cos4.5°= 0.997)?
解:设登到B处,视线BC在C点与地球相切,也就是
看C点,AB就是“楼”的高度,
∴ AB=OB-OA=6389-6370=19(km).
即这层楼至少要高19km,即1900m. 这是不存在的.
在Rt△OCB中,∠O
例2.热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,这栋楼有多高(结果取整数)?
在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
解:如图,α=30,β=60°,AD=120.
∵ tanα= ,tanβ=
∴ BD=AD tanα=120×tan30°=120× =40
CD=AD tanβ=120×tan60°=120×=120
∴ BC=BD+CD=40+120=160≈277(m)
因此,这栋楼高约为277m.
如图,建筑物BC上有一旗杆AB,从与BC相距40m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,求旗杆的高度(结果保留小数点后一位).
解:在Rt△ADC与Rt△BCD中
∵ tan50°= ,tan45°=
∴ AC=40·tan50°≈47.67
BC=40·tan45°=40
∴ AB=AC-BC=47.67-40≈7.7(m)
答:旗杆的高度约为7.7m
例3.如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为30°,已知AB=6m,DE=10m,求乙楼AC的高度(参考数据: ≈1.41,≈1.73,精确到0. 1m).
解:如图,过点E作EF⊥AC于F,则四边形CDEF为矩形.
∴EF=CD,CF=DE=1Om
由题意得∠DAC=∠ADC=45°,∠BEF=30°
设AC=xm,则CD=EF=xm,BF=AC-CF-AB=(x-16)m
在Rt△BEF中,tan∠BEF=
即 ,解得x≈37.8(m)
答:乙楼AC的高度约为37.8m
如图,在数学活动课上,某学习小组在校园内用测量仪测量一棵树的高度,在C处测得,在E处测得,米,仪器高度米,请根据测量的数据计算这棵树的高度(结果精确到0.1米).(参考数据:,,,,,)
解:延长交于H,则易知,
设(米),
,
,
在中,,
,
在中,,
如图,在数学活动课上,某学习小组在校园内用测量仪测量一棵树的高度,在C处测得,在E处测得,米,仪器高度米,请根据测量的数据计算这棵树的高度(结果精确到0.1米).(参考数据:,,,,,)
,
,
即(米);
又,
四边形为矩形,
(米)
答:这棵树AB的高度为米.
1.从一艘船上测得海岸_上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米 B.14米 C.21米 D.42米.
2.身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
A.甲 B.乙 C.丙 D.丁
A
D
3.如图,某航天飞船在地球表面点P的正上方A处,从A处观测到地球表面的最远点Q,若∠QAP=a,地球半径为R,则航天飞船距离地球表面的最近距离AP以及P,Q两点间的地面距离分别是( )
A. B.
C. D.
B
4.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BC0=x,则点A到OC的距离等于( )
A. a·sinx+b·sinx
B. a·cosx+b·cosx
C. a·sinx+b·cosx
D. a·cosx+b·sinx
D
5.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为
_________m.(结果保留根号)
6.如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为______米. (结果保留根号)
5+5
1
7.某公共场所准备改善原有楼梯的安全性能,把倾角由45°减至30°,楼梯高度不变.已知楼梯原长4m,那么调整的楼梯.会增加多长 楼梯多占了多长一段地面
解:在Rt△ABC中,AB=4,∠ABC=45°
∴BC=AC=AB·sin45°=2m
在Rt△ADC中,AC=2,∠ADC=30°
∴AD= m,DC= m
∴AD-AB=(4-4)m,DC-BC=(2-2)m
答:调整后楼梯会增加(4-4)m,占地会加长(2-2)m.
8.如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m)
解:在Rt△ACD中,∠A=30°
∴tan30 °= ∴AC=CD
在Rt△BCD中,∠CBD=60°
∴tan60°= ,∴BC=CD
∵AC-BC=50,∴CD-CD=50 解得,CD≈43
答:该塔约为43m高.
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
解:由题意得,,
则四边形均为矩形.
所以米,米,
在中,,则.设米,
9.八仙阁是八仙山公园里的一个主景区,八仙阁也是晋江的一个标志性建筑.在阁楼上可以看到整个八仙山公园全景,甚至周围景观都能尽收眼底.小明想知道它的高度.于是走到点C处,测得此时塔尖A的仰角是37,向前走了15.5米至点F处,测得此时塔尖A的仰角是,已知小明的眼睛离地面高度是1.5米,请聪明的你帮他求出八仙阁AB的高度.(参考数据:,,)
在中,,
则,即,
解得:,
所以米,
则(米).
答:八仙阁AB的高度为48米.
10.如图,某学习小组在学习了“利用三角函数测高后”,选定测量小河对面一幢建筑物的高度.他们先在斜坡的D处,测得建筑物顶端B的仰角为,且D离地面的高度为9米,坡底的长度米,然后在A处测得建筑物顶端B的仰角为,点E,A,C在同一水平线上,求建筑物的高度.(结果精确到1米,参考数据:)
解:过点作,交于点.
∵,,,
∴四边形为矩形,
∴,米,
又∵,,
∴,
10.如图,某学习小组在学习了“利用三角函数测高后”,选定测量小河对面一幢建筑物的高度.他们先在斜坡的D处,测得建筑物顶端B的仰角为,且D离地面的高度为9米,坡底的长度米,然后在A处测得建筑物顶端B的仰角为,点E,A,C在同一水平线上,求建筑物的高度.(结果精确到1米,参考数据:)
∴,
又∵,
∴,
即,
∴米.
