2022-2023学年高一上学期数学人教A版(2019)必修第一册4.4对数函数 限时训练(含答案)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册4.4对数函数 限时训练(含答案) | 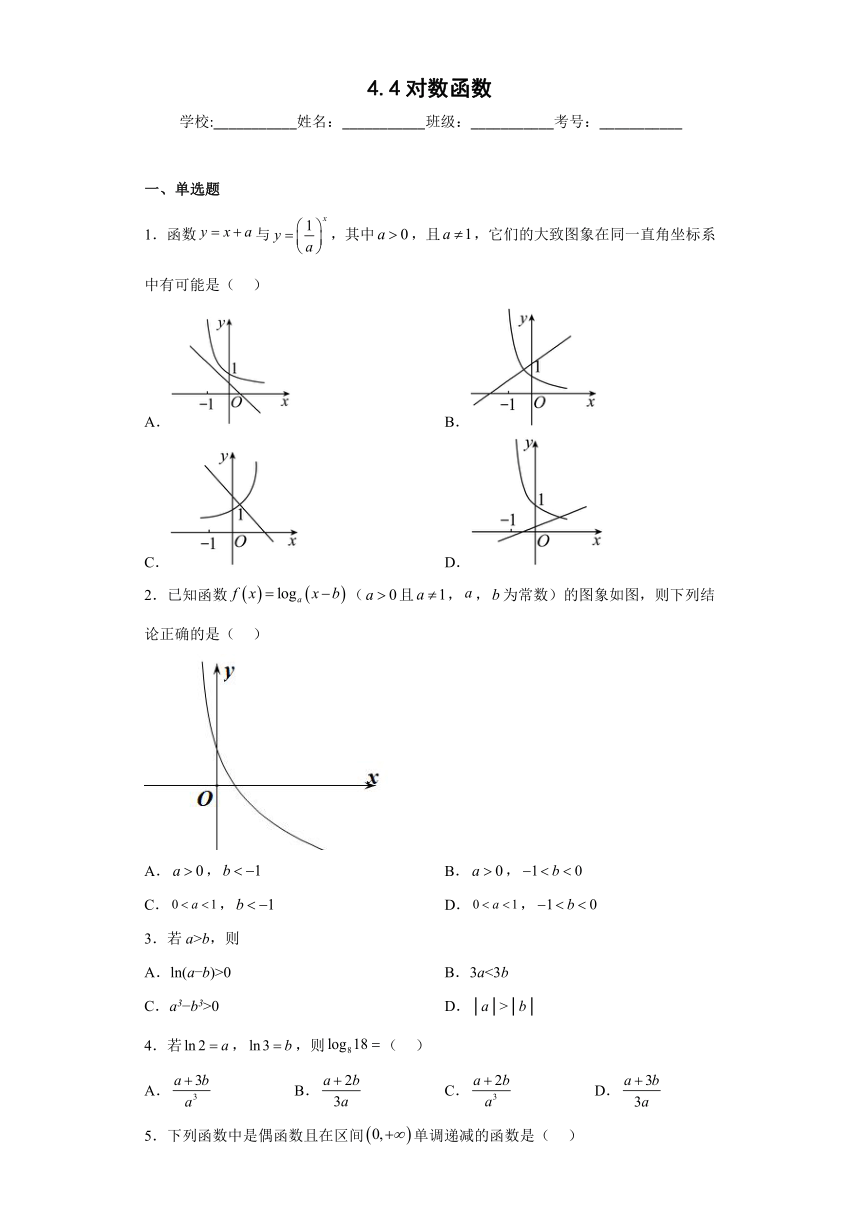 | |
| 格式 | docx | ||
| 文件大小 | 536.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 21:02:03 | ||
图片预览





文档简介
4.4对数函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数与,其中,且,它们的大致图象在同一直角坐标系中有可能是( )
A. B.
C. D.
2.已知函数(且,,为常数)的图象如图,则下列结论正确的是( )
A., B.,
C., D.,
3.若a>b,则
A.ln(a b)>0 B.3a<3b
C.a3 b3>0 D.│a│>│b│
4.若,,则( )
A. B. C. D.
5.下列函数中是偶函数且在区间单调递减的函数是( )
A. B. C. D.
6.函数的单调递减区间是( )
A. B. C. D.
7.设,,则( )
A. B.
C. D.
8.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为
A.1010.1 B.10.1 C.lg10.1 D.
二、多选题
9.,则下列a,b的关系中,不可能成立的有( )
A. B. C. D.
10.设函数=ln(x2-x+1),则下列命题中正确的是( )
A.函数的定义域为R
B.函数是增函数
C.函数的值域为R
D.函数的图象关于直线x=对称
11.若,,则下列表达正确的是( )
A. B.
C. D.
12.若,,则( )
A. B.
C. D.
三、填空题
13.函数的定义域是____________.
14.已知定义在R上的函数在区间上单调递增,且的图象关于对称,若实数a满足,则a的取值范围是___________.
15.已知函数的定义域是R,则实数a的取值范围是___.
四、解答题
16.已知函数.
(1)求函数的解析式;
(2)求的值;
(3)解方程.
17.已知函数.
(1)判断在其定义域上的单调性,并用单调性的定义证明你的结论;
(2)解关于的不等式.
18.如图,某灌溉渠的横断面是等腰梯形,底宽2m,渠深为1.8m,斜坡的倾斜角是45°(无水状态不考虑).
(1)试将横断面中水的面积()表示成水深(m)的函数;
(2)当水深为1.2m时,求横断面中水的面积.
参考答案:
1.B
【解析】利用函数是增函数,排除A,C,然后分别对B,D的图象分析,假设函数的图象是正确的,从而可得的范围,进而可得指数函数的图象
【详解】解:对于A,C,由于函数是增函数,图象应该呈上升趋势,所以A,C错误;
对于B,若函数的图象是正确的,则,所以,所以函数是正确的,所以B正确;
对于D,若函数的图象是正确的,则,所以,所以函数是增函数,所以D错误,
故选:B
2.D
【分析】根据函数图象及对数函数的性质可求解.
【详解】因为函数为减函数,所以
又因为函数图象与轴的交点在正半轴,所以,即
又因为函数图象与轴有交点,所以,所以,
故选:D
3.C
【分析】本题也可用直接法,因为,所以,当时,,知A错,因为是增函数,所以,故B错;因为幂函数是增函数,,所以,知C正确;取,满足,,知D错.
【详解】取,满足,,知A错,排除A;因为,知B错,排除B;取,满足,,知D错,排除D,因为幂函数是增函数,,所以,故选C.
【点睛】本题主要考查对数函数性质、指数函数性质、幂函数性质及绝对值意义,渗透了逻辑推理和运算能力素养,利用特殊值排除即可判断.
4.B
【分析】先换底,然后由对数运算性质可得.
【详解】.
故选:B
5.A
【分析】利用幂指对函数的性质逐一分析给定四个函数的单调性和奇偶性,可得结论.
【详解】解:是偶函数且在区间上单调递减,满足条件;
是非奇非 偶函数,不满足条件;
是偶函数,但在区间上单调递增,不满足条件;
是奇函数不是偶函数,不合题意.
故选:.
6.A
【分析】利用换元法求解,先求出函数的定义域,然后换元,令,则,求出函数的单调区间,再利用“同增异减”可求得答案
【详解】解:由,得,得或,
令(或),则,
因为二次函数在单调递减,在上单调递增,而在定义域内单调递增,
所以的单调递减区间为,
故选:A
7.D
【分析】根据对数函数的性质可得, ,由此可判断得选项.
【详解】解:因为,,所以,所以,故排除A、B选项;
又,且,所以,
故选:D.
8.A
【解析】由题意得到关于的等式,结合对数的运算法则可得亮度的比值.
【详解】两颗星的星等与亮度满足,令,
.
故选A.
【点睛】本题以天文学问题为背景,考查考生的数学应用意识 信息处理能力 阅读理解能力以及指数对数运算.
9.CD
【解析】令结合对数函数图象,分类讨论,,时a,b的关系即可知不成立的选项.
【详解】令,有,
而函数图象如下:
当时,有,有,有,
故选:CD
【点睛】本题考查了对数函数,利用对数函数的性质,结合函数图象判断参数的大小关系,属于基础题.
10.AD
【分析】求得对数型复合函数的定义域、单调性、值域以及对称性,即可判断和选择.
【详解】A正确,∵x2-x+1=>0恒成立,∴函数的定义域为R;
B错误,函数y=ln(x2-x+1)在x>时是增函数,在x<时是减函数;
C错误,由x2-x+1=可得y=ln(x2-x+1)≥,∴函数的值域为;
D正确,,故函数的图象关于直线x=对称.
故选:.
【点睛】本题考查对数型复合函数性质的求解,属综合基础题.
11.AB
【分析】由对数函数和指数函数、幂函数的性质判断.
【详解】解:∵,∴函数在上单调递减,
又∵,
∴,
∴,
即,所以选项A正确,选项B正确,
∵幂函数在上单调递增,且,
∴,所以选项C错误,
∵指数函数在R上单调递减,且,
∴,所以选项D错误,
故选:AB.
12.ACD
【分析】利用指对数的运算性质及其关系求出、、,结合对数函数的单调性判断各选项的正误.
【详解】由题设,,即,A正确;
,即,B错误,D正确;
由,则,C正确;
故选:ACD
13.
【分析】根据分母不为零、真数大于零列不等式组,解得结果.
【详解】由题意得,
故答案为:
【点睛】本题考查函数定义域,考查基本分析求解能力,属基础题.
14.
【分析】由题可判断f(x)为偶函数,再根据单调性即可求解不等式.
【详解】根据题意的图象关于对称,则函数的图象关于y轴对称,即函数为偶函数,
由得,
又由函数在区间上单调递增,
则,
解可得:.
故答案为:.
15.
【分析】问题转化为ax>对于任意实数x恒成立,然后对x分类,再由配方法求最值,即可求得实数a的取值范围.
【详解】解:∵函数的定义域是R,
∴+ax>0对于任意实数x恒成立,
即ax>对于任意实数x恒成立,
当x=0时,上式化为0>﹣1,此式对任意实数a都成立;
当x>0时,则a>=,
∵x>0,∴,则≥,
则≤,可得a>;
当x<0时,则a<,
∵x<0,∴,则>1,
则>1,可得a≤1.
综上可得,实数a的取值范围是.
故答案为:.
16.(1);(2)1;(3)或.
【分析】(1)利用方程组法求解,把函数中的换成,得到一个式子,然后和已知的函数关系式联立方程组可求出的解析式;
(2)直接代值求解;
(3)由题意可得,化简可求得结果.
【详解】解:(1)函数的定义域为,
,①
上式中把换成,得,
即.②
将②代入①,得,
∴.
(2).
(3)∵,
∴,可得,
解得或,
∴或.
17.(1)在R上是增函数,证明见解析;(2).
【分析】(1)由题可判断函数为奇函数且为增函数,利用定义法的步骤证明即可;
(2)利用函数的单调性及对数函数的单调性即解.
【详解】(1),则函数是奇函数,
则当时,设,
则
,
,
,即,,
则,即,
则在,上是增函数,
是上的奇函数,
在上是增函数.
(2)在上是增函数,
不等式等价为不等式,
即.
即不等式的解集为.
18.(1)
(2)3.84
【分析】(1)根据给定条件利用梯形的面积公式列式化简即得.
(2)由(1)得出的函数的解析式,代入计算可得答案.
(1)
依题意,横断面中的水面是下底为2m,上底为m,高为h m的等腰梯形,
所以.
(2)
由(1)知,,,
所以当水深为1.2m时,横断面水中的面积为3.84.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数与,其中,且,它们的大致图象在同一直角坐标系中有可能是( )
A. B.
C. D.
2.已知函数(且,,为常数)的图象如图,则下列结论正确的是( )
A., B.,
C., D.,
3.若a>b,则
A.ln(a b)>0 B.3a<3b
C.a3 b3>0 D.│a│>│b│
4.若,,则( )
A. B. C. D.
5.下列函数中是偶函数且在区间单调递减的函数是( )
A. B. C. D.
6.函数的单调递减区间是( )
A. B. C. D.
7.设,,则( )
A. B.
C. D.
8.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为
A.1010.1 B.10.1 C.lg10.1 D.
二、多选题
9.,则下列a,b的关系中,不可能成立的有( )
A. B. C. D.
10.设函数=ln(x2-x+1),则下列命题中正确的是( )
A.函数的定义域为R
B.函数是增函数
C.函数的值域为R
D.函数的图象关于直线x=对称
11.若,,则下列表达正确的是( )
A. B.
C. D.
12.若,,则( )
A. B.
C. D.
三、填空题
13.函数的定义域是____________.
14.已知定义在R上的函数在区间上单调递增,且的图象关于对称,若实数a满足,则a的取值范围是___________.
15.已知函数的定义域是R,则实数a的取值范围是___.
四、解答题
16.已知函数.
(1)求函数的解析式;
(2)求的值;
(3)解方程.
17.已知函数.
(1)判断在其定义域上的单调性,并用单调性的定义证明你的结论;
(2)解关于的不等式.
18.如图,某灌溉渠的横断面是等腰梯形,底宽2m,渠深为1.8m,斜坡的倾斜角是45°(无水状态不考虑).
(1)试将横断面中水的面积()表示成水深(m)的函数;
(2)当水深为1.2m时,求横断面中水的面积.
参考答案:
1.B
【解析】利用函数是增函数,排除A,C,然后分别对B,D的图象分析,假设函数的图象是正确的,从而可得的范围,进而可得指数函数的图象
【详解】解:对于A,C,由于函数是增函数,图象应该呈上升趋势,所以A,C错误;
对于B,若函数的图象是正确的,则,所以,所以函数是正确的,所以B正确;
对于D,若函数的图象是正确的,则,所以,所以函数是增函数,所以D错误,
故选:B
2.D
【分析】根据函数图象及对数函数的性质可求解.
【详解】因为函数为减函数,所以
又因为函数图象与轴的交点在正半轴,所以,即
又因为函数图象与轴有交点,所以,所以,
故选:D
3.C
【分析】本题也可用直接法,因为,所以,当时,,知A错,因为是增函数,所以,故B错;因为幂函数是增函数,,所以,知C正确;取,满足,,知D错.
【详解】取,满足,,知A错,排除A;因为,知B错,排除B;取,满足,,知D错,排除D,因为幂函数是增函数,,所以,故选C.
【点睛】本题主要考查对数函数性质、指数函数性质、幂函数性质及绝对值意义,渗透了逻辑推理和运算能力素养,利用特殊值排除即可判断.
4.B
【分析】先换底,然后由对数运算性质可得.
【详解】.
故选:B
5.A
【分析】利用幂指对函数的性质逐一分析给定四个函数的单调性和奇偶性,可得结论.
【详解】解:是偶函数且在区间上单调递减,满足条件;
是非奇非 偶函数,不满足条件;
是偶函数,但在区间上单调递增,不满足条件;
是奇函数不是偶函数,不合题意.
故选:.
6.A
【分析】利用换元法求解,先求出函数的定义域,然后换元,令,则,求出函数的单调区间,再利用“同增异减”可求得答案
【详解】解:由,得,得或,
令(或),则,
因为二次函数在单调递减,在上单调递增,而在定义域内单调递增,
所以的单调递减区间为,
故选:A
7.D
【分析】根据对数函数的性质可得, ,由此可判断得选项.
【详解】解:因为,,所以,所以,故排除A、B选项;
又,且,所以,
故选:D.
8.A
【解析】由题意得到关于的等式,结合对数的运算法则可得亮度的比值.
【详解】两颗星的星等与亮度满足,令,
.
故选A.
【点睛】本题以天文学问题为背景,考查考生的数学应用意识 信息处理能力 阅读理解能力以及指数对数运算.
9.CD
【解析】令结合对数函数图象,分类讨论,,时a,b的关系即可知不成立的选项.
【详解】令,有,
而函数图象如下:
当时,有,有,有,
故选:CD
【点睛】本题考查了对数函数,利用对数函数的性质,结合函数图象判断参数的大小关系,属于基础题.
10.AD
【分析】求得对数型复合函数的定义域、单调性、值域以及对称性,即可判断和选择.
【详解】A正确,∵x2-x+1=>0恒成立,∴函数的定义域为R;
B错误,函数y=ln(x2-x+1)在x>时是增函数,在x<时是减函数;
C错误,由x2-x+1=可得y=ln(x2-x+1)≥,∴函数的值域为;
D正确,,故函数的图象关于直线x=对称.
故选:.
【点睛】本题考查对数型复合函数性质的求解,属综合基础题.
11.AB
【分析】由对数函数和指数函数、幂函数的性质判断.
【详解】解:∵,∴函数在上单调递减,
又∵,
∴,
∴,
即,所以选项A正确,选项B正确,
∵幂函数在上单调递增,且,
∴,所以选项C错误,
∵指数函数在R上单调递减,且,
∴,所以选项D错误,
故选:AB.
12.ACD
【分析】利用指对数的运算性质及其关系求出、、,结合对数函数的单调性判断各选项的正误.
【详解】由题设,,即,A正确;
,即,B错误,D正确;
由,则,C正确;
故选:ACD
13.
【分析】根据分母不为零、真数大于零列不等式组,解得结果.
【详解】由题意得,
故答案为:
【点睛】本题考查函数定义域,考查基本分析求解能力,属基础题.
14.
【分析】由题可判断f(x)为偶函数,再根据单调性即可求解不等式.
【详解】根据题意的图象关于对称,则函数的图象关于y轴对称,即函数为偶函数,
由得,
又由函数在区间上单调递增,
则,
解可得:.
故答案为:.
15.
【分析】问题转化为ax>对于任意实数x恒成立,然后对x分类,再由配方法求最值,即可求得实数a的取值范围.
【详解】解:∵函数的定义域是R,
∴+ax>0对于任意实数x恒成立,
即ax>对于任意实数x恒成立,
当x=0时,上式化为0>﹣1,此式对任意实数a都成立;
当x>0时,则a>=,
∵x>0,∴,则≥,
则≤,可得a>;
当x<0时,则a<,
∵x<0,∴,则>1,
则>1,可得a≤1.
综上可得,实数a的取值范围是.
故答案为:.
16.(1);(2)1;(3)或.
【分析】(1)利用方程组法求解,把函数中的换成,得到一个式子,然后和已知的函数关系式联立方程组可求出的解析式;
(2)直接代值求解;
(3)由题意可得,化简可求得结果.
【详解】解:(1)函数的定义域为,
,①
上式中把换成,得,
即.②
将②代入①,得,
∴.
(2).
(3)∵,
∴,可得,
解得或,
∴或.
17.(1)在R上是增函数,证明见解析;(2).
【分析】(1)由题可判断函数为奇函数且为增函数,利用定义法的步骤证明即可;
(2)利用函数的单调性及对数函数的单调性即解.
【详解】(1),则函数是奇函数,
则当时,设,
则
,
,
,即,,
则,即,
则在,上是增函数,
是上的奇函数,
在上是增函数.
(2)在上是增函数,
不等式等价为不等式,
即.
即不等式的解集为.
18.(1)
(2)3.84
【分析】(1)根据给定条件利用梯形的面积公式列式化简即得.
(2)由(1)得出的函数的解析式,代入计算可得答案.
(1)
依题意,横断面中的水面是下底为2m,上底为m,高为h m的等腰梯形,
所以.
(2)
由(1)知,,,
所以当水深为1.2m时,横断面水中的面积为3.84.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
