八年级数学上册第一章图像的全等单元复习题
文档属性
| 名称 | 八年级数学上册第一章图像的全等单元复习题 |  | |
| 格式 | zip | ||
| 文件大小 | 174.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-31 11:13:47 | ||
图片预览

文档简介
第一章检测卷
总分100分 时间90分钟 成绩评定
一、看一看,选一选(每题3分,共30分)
1.A 在△ABC中, ∠C=∠B,与△ABC全等的三角形有一个角是100°,那么△ABC中与这个角对应的角是 ( )
A.∠B B.∠A C.∠C D.∠B或∠C
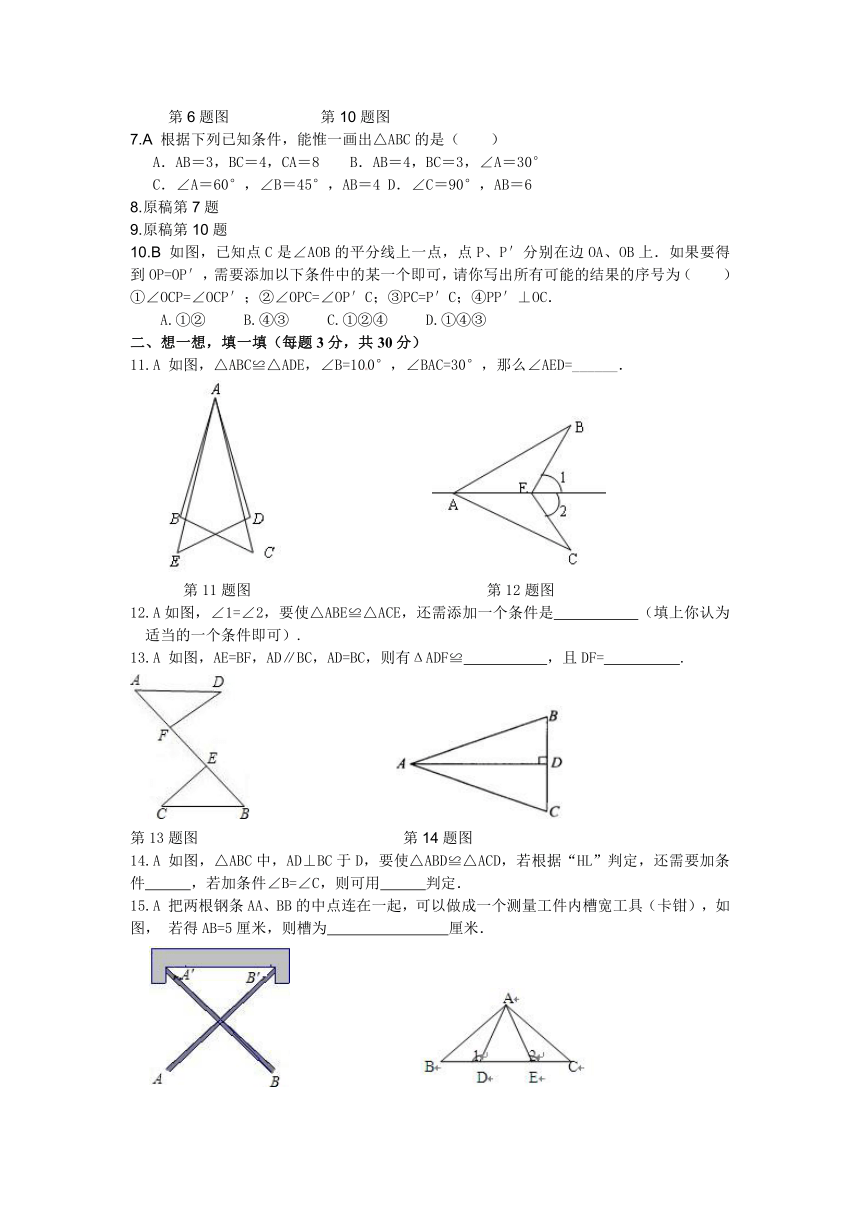
2.A 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
第2题图 第3题图
3.A 如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS C.AAS D.ASA
4. 如图是一个风筝设计图,其主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,且AB≠AD,则下列判断不正确的是( )
A.△ABD≌△CBD B.△ABC≌△ADC C.△AOB≌△COB D.△AOD≌△COD
第4题图 第5题图
5. 如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A.△ACE≌△BCD B.△BGC≌△AFC C.△DCG≌△ECF D.△ADB≌△CEA
6.A 在△ABC中,∠A=90°,CD平分∠ACB,DE⊥BC于点E,若AB=6,则DE+DB=( )
A.4 B. 5 C. 6 D. 7
第6题图 第10题图
7.A 根据下列已知条件,能惟一画出△ABC的是( )
A.AB=3,BC=4,CA=8 B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=6
8.原稿第7题
9.原稿第10题
10.B 如图,已知点C是∠AOB的平分线上一点,点P、P′分别在边OA、OB上.如果要得到OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能的结果的序号为( )
①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
A.①② B.④③ C.①②④ D.①④③
二、想一想,填一填(每题3分,共30分)
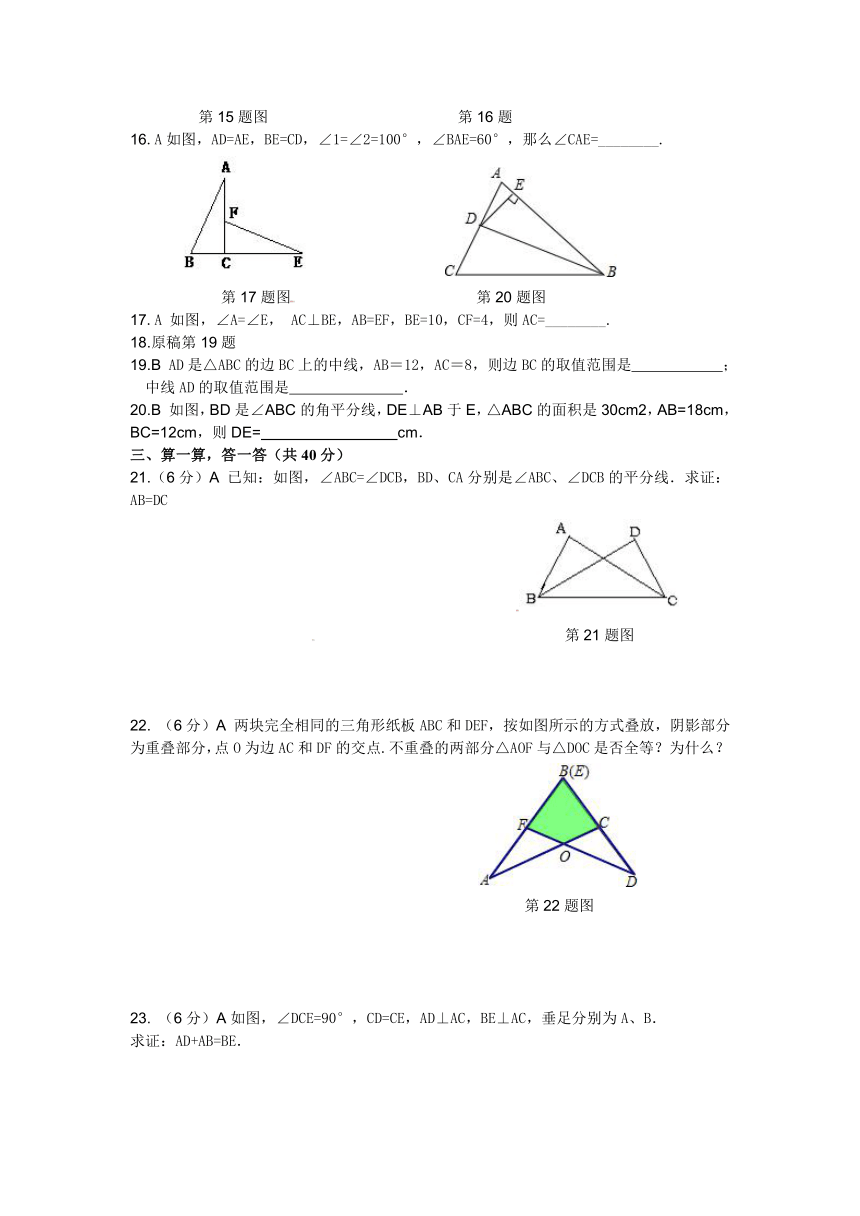
11.A 如图,△ABC≌△ADE,∠B=100°,∠BAC=30°,那么∠AED=______.
第11题图 第12题图
12.A如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是 (填上你认为适当的一个条件即可).
13.A 如图,AE=BF,AD∥BC,AD=BC,则有ΔADF≌ ,且DF= .
第13题图 第14题图
14.A 如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件 ,若加条件∠B=∠C,则可用 判定.
15.A 把两根钢条AA、BB的中点连在一起,可以做成一个测量工件内槽宽工具(卡钳),如图, 若得AB=5厘米,则槽为 厘米.
第15题图 第16题
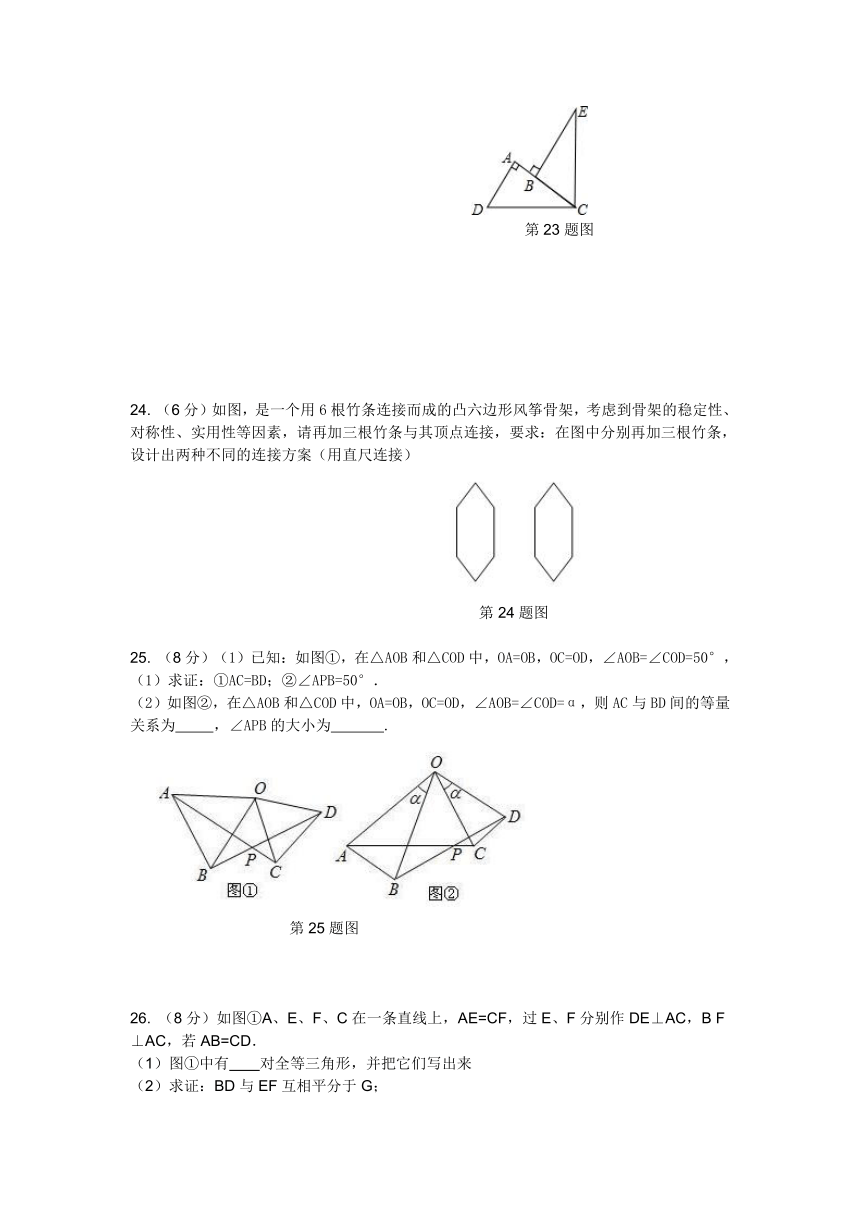
16.A如图,AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,那么∠CAE=________.
第17题图 第20题图
17.A 如图,∠A=∠E, AC⊥BE,AB=EF,BE=10,CF=4,则AC=________.
18.原稿第19题
19.B AD是△ABC的边BC上的中线,AB=12,AC=8,则边BC的取值范围是 ;中线AD的取值范围是 .
20.B 如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=18cm,BC=12cm,则DE= cm.
三、算一算,答一答(共40分)
21.(6分)A 已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC
第21题图
22. (6分)A 两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等?为什么?
第22题图
23. (6分)A如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B.
求证:AD+AB=BE.
第23题图
24. (6分)如图,是一个用6根竹条连接而成的凸六边形风筝骨架,考虑到骨架的稳定性、对称性、实用性等因素,请再加三根竹条与其顶点连接,要求:在图中分别再加三根竹条,设计出两种不同的连接方案(用直尺连接)
第24题图
25. (8分)(1)已知:如图①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°,(1)求证:①AC=BD;②∠APB=50°.
(2)如图②,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD间的等量关系为 ,∠APB的大小为 .
第25题图
26. (8分)如图①A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,B F⊥AC,若AB=CD.
(1)图①中有 对全等三角形,并把它们写出来
(2)求证:BD与EF互相平分于G;
(3)若将△ABF的边AF沿GA方向移动变为图②时,其余条件不变,第(2)题中的结论是否成立,如果成立,请予证明.
第26题图
一、1.D 点拨:∵一个三角形中只能有一个钝角.∴100°的角只能是等腰三角形中的顶角.∴∠B=∠C是底角,∠A是顶角,∴△ABC中与这个角对应的角是∠A.
2.C
3.D 点拨:亮亮可以量取∠A和∠C度数,AC的长度,利用ASA画一个和书上完全一样的三角形.
4.B
5.D
6.C 点拨:根据角平分线性质可知AD=DE,所以DE+DB=AD+BD=AB=6.
7.B 点拨:A中AC与BC两边之差大于第三边,所以A不能作出三角形;B中两角夹一边,形状固定,所以可作唯一三角形;C中∠A并不是AB,BC的夹角,所以可画出多个三角形;D中两个锐角也不确定,也可画出多个三角形.
10.C 点拨:①若加∠OCP=∠OCP′,则根据ASA可证明△OPC≌△OP′C,得OP=OP′;②若加∠OPC=∠OP′C,则根据AAS可证明△OPC≌△OP′C,得OP=OP′;③若加PC=P′C,则不能证明△OPC≌△OP′C,不能得到OP=OP′;④若加PP′⊥OC,则根据ASA可证明△OPC≌△OP′C,得OP=OP′.
二、11.50°
12.答案不唯一,如∠B=∠C等
13.△BCE,CE
14. AB=ACAB=AC,AAS
15.5 点拨:连接AB,A′B′,O为AB′和BA′的中点,∴OA′=OB,OA=OB′,∵∠A′OB′=∠AOB∴△OA′B′≌△OAB,即A′B′=AB,故A′B′=5cm.
16. 40° 点拨:∵∠1=∠2=100°,∴∠ADE=∠AED=80°,∴∠DAE=20°,在△BAE和△CAD中,AD=AE,∠ADE=∠AED ,BE=CD,∴△BAE≌△CAD,∴∠CAD=∠BAE=60°,∴∠CAE=40°.
17.6
19. 4<BC<20,2<AD<10 点拨:在△ABC中,则AB-AC<BC<AB+AC,即12-8<BC<12+8,4<BC<20,延长AD至点E,使AD=DE,连接BE,∵AD是△ABC的边BC上的中线,∴BD=CD,又∠ADC=∠BDE,AD=DE∴△ACD≌△EBD,∴BE=AC,
在△ABE中,AB-BE<AE<AB+BE,即AB-AC<AE<AB+AC,12-8<AE<12+8,即4<AE<20,∴2<AD<10.
20.2 点拨:过点D,作DF⊥BC,垂足为点F∵BD是∠ABC的角平分线,DE⊥AB,∴DE=DF,∵△ABC的面积是30cm2,AB=18cm,BC=12cm,∴S△ABC=DE AB+DF BC,即×18×DE+×12×DE=30,∴DE=2(cm).
21. ∵∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线,
∴∠ACB=∠DBC,
在△ABC与△DCB中,
∴△ABC≌△DCB,
∴AB=DC.
22. 全等.理由如下:
∵两三角形纸板完全相同,
∴BC=BF,AB=BD,∠A=∠D,
∴AB-BF=BD-BC,即AF=DC.
在△AOF和△DOC中,
∴△AOF≌△DOC(AAS).
23. ∵∠DCE=90°(已知),
∴∠ECB+∠ACD=90°,
∵EB⊥AC,
∴∠E+∠ECB=90°.
∴∠ACD=∠E.
∵AD⊥AC,BE⊥AC,
∴∠A=∠EBC=90°.
在Rt△ACD和Rt△BEC中,
∴Rt△ACD≌Rt△BEC(AAS).
∴AD=BC,AC=BE,
∴AD+AB=BC+AB=AC.
∴AD+AB=BE.
24.
25. ∵∠AOB=∠COD=50°,∴∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,∴∠APB=∠AOB=50°.
(2)相等,∠APB=α.
26. (1)图①中有3对全等三角形,它们是△AFB≌△DEC,△DEG≌△BFG,△AGB≌△CGD.
(2)∵DE⊥AC,B F⊥AC,
∴∠AFB=∠CED=90°
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵AB=CD,
∴△ABF≌△CDE,
∴ED=BF.
由∠AFB=∠CED=90°得DE∥BF,
∴∠EDG=∠GBF,
∵∠EGD和∠FGB是对顶角,ED=BF,
△DEG≌△BFG,
∴EG=FG,DG=BG,
∴BD与EF互相平分于G;
(3)第(2)题中的结论成立,
理由:∵AE=CF,
∴AE-EF=CF-EF,即AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
∵AB=CD,
∴△ABF≌△CED,
∴BF=ED.
∵∠BFG=∠DEG=90°,
∴BF∥ED,
∴∠FBG=∠EDG,
∴△BFG≌△DEG,
∴FG=GE,BG=GD,
即第(2)题中的结论仍然成立.
总分100分 时间90分钟 成绩评定
一、看一看,选一选(每题3分,共30分)
1.A 在△ABC中, ∠C=∠B,与△ABC全等的三角形有一个角是100°,那么△ABC中与这个角对应的角是 ( )
A.∠B B.∠A C.∠C D.∠B或∠C
2.A 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
第2题图 第3题图
3.A 如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS C.AAS D.ASA
4. 如图是一个风筝设计图,其主体部分(四边形ABCD)关于BD所在的直线对称,AC与BD相交于点O,且AB≠AD,则下列判断不正确的是( )
A.△ABD≌△CBD B.△ABC≌△ADC C.△AOB≌△COB D.△AOD≌△COD
第4题图 第5题图
5. 如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A.△ACE≌△BCD B.△BGC≌△AFC C.△DCG≌△ECF D.△ADB≌△CEA
6.A 在△ABC中,∠A=90°,CD平分∠ACB,DE⊥BC于点E,若AB=6,则DE+DB=( )
A.4 B. 5 C. 6 D. 7
第6题图 第10题图
7.A 根据下列已知条件,能惟一画出△ABC的是( )
A.AB=3,BC=4,CA=8 B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=6
8.原稿第7题
9.原稿第10题
10.B 如图,已知点C是∠AOB的平分线上一点,点P、P′分别在边OA、OB上.如果要得到OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能的结果的序号为( )
①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
A.①② B.④③ C.①②④ D.①④③
二、想一想,填一填(每题3分,共30分)
11.A 如图,△ABC≌△ADE,∠B=100°,∠BAC=30°,那么∠AED=______.
第11题图 第12题图
12.A如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是 (填上你认为适当的一个条件即可).
13.A 如图,AE=BF,AD∥BC,AD=BC,则有ΔADF≌ ,且DF= .
第13题图 第14题图
14.A 如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件 ,若加条件∠B=∠C,则可用 判定.
15.A 把两根钢条AA、BB的中点连在一起,可以做成一个测量工件内槽宽工具(卡钳),如图, 若得AB=5厘米,则槽为 厘米.
第15题图 第16题
16.A如图,AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,那么∠CAE=________.
第17题图 第20题图
17.A 如图,∠A=∠E, AC⊥BE,AB=EF,BE=10,CF=4,则AC=________.
18.原稿第19题
19.B AD是△ABC的边BC上的中线,AB=12,AC=8,则边BC的取值范围是 ;中线AD的取值范围是 .
20.B 如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=18cm,BC=12cm,则DE= cm.
三、算一算,答一答(共40分)
21.(6分)A 已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC
第21题图
22. (6分)A 两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等?为什么?
第22题图
23. (6分)A如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B.
求证:AD+AB=BE.
第23题图
24. (6分)如图,是一个用6根竹条连接而成的凸六边形风筝骨架,考虑到骨架的稳定性、对称性、实用性等因素,请再加三根竹条与其顶点连接,要求:在图中分别再加三根竹条,设计出两种不同的连接方案(用直尺连接)
第24题图
25. (8分)(1)已知:如图①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°,(1)求证:①AC=BD;②∠APB=50°.
(2)如图②,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD间的等量关系为 ,∠APB的大小为 .
第25题图
26. (8分)如图①A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,B F⊥AC,若AB=CD.
(1)图①中有 对全等三角形,并把它们写出来
(2)求证:BD与EF互相平分于G;
(3)若将△ABF的边AF沿GA方向移动变为图②时,其余条件不变,第(2)题中的结论是否成立,如果成立,请予证明.
第26题图
一、1.D 点拨:∵一个三角形中只能有一个钝角.∴100°的角只能是等腰三角形中的顶角.∴∠B=∠C是底角,∠A是顶角,∴△ABC中与这个角对应的角是∠A.
2.C
3.D 点拨:亮亮可以量取∠A和∠C度数,AC的长度,利用ASA画一个和书上完全一样的三角形.
4.B
5.D
6.C 点拨:根据角平分线性质可知AD=DE,所以DE+DB=AD+BD=AB=6.
7.B 点拨:A中AC与BC两边之差大于第三边,所以A不能作出三角形;B中两角夹一边,形状固定,所以可作唯一三角形;C中∠A并不是AB,BC的夹角,所以可画出多个三角形;D中两个锐角也不确定,也可画出多个三角形.
10.C 点拨:①若加∠OCP=∠OCP′,则根据ASA可证明△OPC≌△OP′C,得OP=OP′;②若加∠OPC=∠OP′C,则根据AAS可证明△OPC≌△OP′C,得OP=OP′;③若加PC=P′C,则不能证明△OPC≌△OP′C,不能得到OP=OP′;④若加PP′⊥OC,则根据ASA可证明△OPC≌△OP′C,得OP=OP′.
二、11.50°
12.答案不唯一,如∠B=∠C等
13.△BCE,CE
14. AB=ACAB=AC,AAS
15.5 点拨:连接AB,A′B′,O为AB′和BA′的中点,∴OA′=OB,OA=OB′,∵∠A′OB′=∠AOB∴△OA′B′≌△OAB,即A′B′=AB,故A′B′=5cm.
16. 40° 点拨:∵∠1=∠2=100°,∴∠ADE=∠AED=80°,∴∠DAE=20°,在△BAE和△CAD中,AD=AE,∠ADE=∠AED ,BE=CD,∴△BAE≌△CAD,∴∠CAD=∠BAE=60°,∴∠CAE=40°.
17.6
19. 4<BC<20,2<AD<10 点拨:在△ABC中,则AB-AC<BC<AB+AC,即12-8<BC<12+8,4<BC<20,延长AD至点E,使AD=DE,连接BE,∵AD是△ABC的边BC上的中线,∴BD=CD,又∠ADC=∠BDE,AD=DE∴△ACD≌△EBD,∴BE=AC,
在△ABE中,AB-BE<AE<AB+BE,即AB-AC<AE<AB+AC,12-8<AE<12+8,即4<AE<20,∴2<AD<10.
20.2 点拨:过点D,作DF⊥BC,垂足为点F∵BD是∠ABC的角平分线,DE⊥AB,∴DE=DF,∵△ABC的面积是30cm2,AB=18cm,BC=12cm,∴S△ABC=DE AB+DF BC,即×18×DE+×12×DE=30,∴DE=2(cm).
21. ∵∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线,
∴∠ACB=∠DBC,
在△ABC与△DCB中,
∴△ABC≌△DCB,
∴AB=DC.
22. 全等.理由如下:
∵两三角形纸板完全相同,
∴BC=BF,AB=BD,∠A=∠D,
∴AB-BF=BD-BC,即AF=DC.
在△AOF和△DOC中,
∴△AOF≌△DOC(AAS).
23. ∵∠DCE=90°(已知),
∴∠ECB+∠ACD=90°,
∵EB⊥AC,
∴∠E+∠ECB=90°.
∴∠ACD=∠E.
∵AD⊥AC,BE⊥AC,
∴∠A=∠EBC=90°.
在Rt△ACD和Rt△BEC中,
∴Rt△ACD≌Rt△BEC(AAS).
∴AD=BC,AC=BE,
∴AD+AB=BC+AB=AC.
∴AD+AB=BE.
24.
25. ∵∠AOB=∠COD=50°,∴∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,∴∠APB=∠AOB=50°.
(2)相等,∠APB=α.
26. (1)图①中有3对全等三角形,它们是△AFB≌△DEC,△DEG≌△BFG,△AGB≌△CGD.
(2)∵DE⊥AC,B F⊥AC,
∴∠AFB=∠CED=90°
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵AB=CD,
∴△ABF≌△CDE,
∴ED=BF.
由∠AFB=∠CED=90°得DE∥BF,
∴∠EDG=∠GBF,
∵∠EGD和∠FGB是对顶角,ED=BF,
△DEG≌△BFG,
∴EG=FG,DG=BG,
∴BD与EF互相平分于G;
(3)第(2)题中的结论成立,
理由:∵AE=CF,
∴AE-EF=CF-EF,即AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
∵AB=CD,
∴△ABF≌△CED,
∴BF=ED.
∵∠BFG=∠DEG=90°,
∴BF∥ED,
∴∠FBG=∠EDG,
∴△BFG≌△DEG,
∴FG=GE,BG=GD,
即第(2)题中的结论仍然成立.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
