江西省南昌市三校2022-2023学年高三上学期第一次联考(11月期中考试)数学(理)试题(pdf 含答案)
文档属性
| 名称 | 江西省南昌市三校2022-2023学年高三上学期第一次联考(11月期中考试)数学(理)试题(pdf 含答案) |  | |
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 20:51:38 | ||
图片预览




文档简介
南昌市三校 高三上学期第 -次联考
数学试卷〈理科〉
命题人z涂方珍 学校z南昌十中 考试时长: 120分钟 试卷总分: 150分
一、选择题: (本题共12小题, 每小题5分, 共60分.在每小题给出的四个选项中, 只有一
项是符合题目要求的.〉
l已知集合M十二子。)叫(| 升到)则MnN=C
A. [-4,-1] B.[-l,3) c.[-4,3) D. [-1,3]
2. 设平而向窒石, E均为单位!句蠢,贝I] “ 1ci-2E1 12ri + E1 ”是 "ri .L E”= 的〈 〉
A充分而不必要条件 B.必要而不充分条件
c. 充分必要条件 D.既不充分也不必要条件
3. 己知函数 f(x)=t''
x. 0, 则f(ln2) =
lf(x -1), x > 0
2
-4 A. 甲 B. C. 2e D. 4e
e
4 虫11 图,在 今 ABC中, BN = 扣,设五百 = a, Al斗,则五百=( )
A. 『 3- 3『 1- 1- 3- :i『 1-α--b - B. -a--b C . -a +-b D. -a +-b
4 4
5.如|望所示 . 在平面直角坐标系中 , 角α和角β均以 Ox 为始边. 终边分别为射线 OA和 OB , 射线 OA,
与单位圆的交点分别为Al(- 3
π
oc ,-4 11, C(-1,0) 着 LBOC = 一 , 贝ljcos(β- α)的值是(
5 5) 6
A. -叫
5 B. 3+4.jj
IO 10
I '1,('., I ,
c. 4-3
-fS
D. 4+3.jj
<:
IO 10
6通过研究正五边形和正十边形的作囚,古希腊数学家毕达哥拉斯发现了黄金分割率,黄金分割率的值也
‘反-I J石二骂王
可以归川
A. -2 B. -J2 c . .fi. o.Js-1
高三数学(理科)三校联考试卷 第1页(共4页)
7己知过点 A (α,0)作曲线 'y = (t-x)e 的切线有且仅有l条 , 贝归=〈 〉
A.-3 B.3 c.-3或1 D. 3或l
8己知何数f(明R上是增函数若α =-f(I咱i), b=f(l唱4.1), c=f(俨勺,则日, b, c的大小关系
为( )
A. a9.在A ABC 中 , 角 A 8, C F斤对的边分别为 a, b, c. 若 2acos C + b = 2c cos A . c = ...[3a , 贝IJ LA=(
A. 1t B.π c.2: o.I主
6 4 3 3
10.已知函数/(们{(气?当二飞\5'8,若数列{向}满足an = f(η)(nεN*)且{时是递晰列,则实数α的取
值?也图是( )
A. (2,3) B.(2,3) c.(!,3) D.[!,3)
π
11. 已知函数 f(x) = 2sin(x +伊)cosx-sinψ(|ψ|〈 -2 ) , 且对于任意x E R , 都有 't (x+-)=-f(--x). 下列3 3
ππ 、 J也 γ .11
序号中 , ① f(x) 在区间[-一6 ’-6 ]上单调递增’ ②/(0)=工
-
2 , ③着!( 2 )-丘 , 贝iJ f(xo -一12 )=一3 3 ,
④
4π
着实数m使得为程 f(x)-m = 。在(0,τ)上恰有与·勺 , 以X1ω
x 口+、,& x +x -π 的
3 正 确 序亏有
A①②③ B.①③④ c. ①②④ D.②③④
12.黎曼函数 R(x)是一个特殊函数 . 由德国数学家黎曼发现并提出 , 该函数定义在(0, 1)上 . 当x =!巾q,
都是正整数,:为最俏真分数)时,R(们 i;当x=O或1或x为CO, 1)内的无理数毗 R(x) = 0.若9
(x + 1)1'1偶 l苟 敛, g(x + 2);但奇民数,当xε(0,1)时, g(x) = R(x) 则, (
A.g(平)>抖 (cos2创川的主 g(cos2圳(呻)
(平)>i且g(co内呻)三 g(cos2B.g 彻(的)
C.g(平)=如(cos2阳印)三 g(co泸α)g(si
D.g(平)=i g(cos2且 asi训)三 g(c的)仰in2{3)
二、填空题(本题共 4 小题, 每小题 5 分, 共 20 分〉
高三数学(理科)三校联考试卷 第2页(共4页)
13 已知aeR若复数z = a2-a-2 + (α2 +3α + 2)i为纯虚数 , 贝1Ja = 一一一一一一
14.如图 , 扇环ABCD 巾,弧AD=4,弧ic = 2, IABI = 1co1 = 1,
Yrn扇1不ABCD的面积S = ·
一一一一 ·(;二〉
15 已知函数 f(x) 是定义域为 R 的奇函数 . 当 x>O 时 ’, / (-x) > 2/(x) , 且 f(3)=0 , 则不等式
f(x)>O 的解的一一一
16.锐角A ABC中 , α , b, c为角A, B, C所对的边 , 点C为A ABC的重心 , 若AG .l BG,则cosC的取值范
图为
三、简答题〈本题共 5 小题,每小题 12 分,共 60 分〉
l 7 . (12 分)已知函数f(x) = 1-J'Jsin2x + 2cos与
(1)求f(x)的最大值及取得最大值的的x集合J
(2)设A ABC的角A, B, C的对边分别为α , b, c , 且α= 1, f(A) = 0求. b+c的取值范围
18. (12分)如图,在三棱柱 ABC-A1 B1C1 中,侧面AA I C ,IC .L底面AβC 侧面AA CC是菱形 ,1 1
LA AC = 60'「 . ζA CB=90° , AC=BC=2I
c,
(1 )若D为A C的中点 , 求证: AD.LA
1 I B;
2( )求二面角 A-A1C-B1 的正弦僵
B
19. 1( 2分)某校组织围棋比赛, 每场比赛采用五局三胜制( 一方先胜三局即获胜 , 比赛结束)、 比赛采
用积分制 , 积分规则如下 每场比赛中 , 如果四局及四局以内结束比赛 , 取胜的一方积 3 分. 负者积 0
分j五局结束比赛 . 取胜的一方积2分负者积1分已知甲乙丙人比赛 . 甲每局获胜的概率 为士
(1 )在一场比赛中 , 甲的积分为X, 求X的概率分布列 ,
高三数学(理科)三校联考试卷 第3页(共4页)
(2)求甲在参加三场比赛后 , 积分之和为5分的概率
20 (12分)己知困C: (x -1)2 + 2 y = l 椭圆M 王: + 丘, = l .
8 4
( l)求-liE:因 ctt椭圆M内:
(2)若因C的切J线m与椭圆 M 交于 P, Q 两点 , F为椭圆M伯右焦点 , 求A FPQ 丽积的最大值 .
21时)已知函数f叫i~) tox 卡叫
(l)若 f(x) 在(O,+oo)单调递增 , 求。的值.
I 3
(2)当-<α x< - e 时 , 设函数 g(x)-_ f( ) 一一- 的:最小值为h(α) , 求函数 h(α)的值城 .
4 4 x
四、选{故题
22 ( 10分)[选修4.4: 坐标系与参数为程]
lI x=a.+-.J3 二-t
在平商直角坐标x0,中 , 直线l的参数方程为{I 2 (I 为参数, 。 为常数) 以原点。为极点, x
l
I v=-t
L 2
4cosθ
轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ= --:-:;-::-
sm 11
(1 )求直线l的普通方程和lffi线C的直角坐标方程:
(2)设直线l与曲线C相交于 A,B 网点 , 若IABI = 16 , 求。 的值.
23 (10分)[选修4-5: 不等式选讲 l
已知函数f(x) =Ix+αl+2lx-lj.
( l)当α=2时 , 求不等式 f(x) 至4的解集j
(2)若 3x E (1,2) , 使得不等式 f(x) >川成立 , 求实数。的取值范围。
高三数学(理科)三校联考试卷 第4页(共4页)
高三上学期第-次三校联考数学(理科〉试卷参考答案及评分标准
一、选择题: (本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的. 〉
|序号I 1 I2 I 3 I 4 I s I 6 I 1 I s I 9 I 10 I 11 I 12 I
|答案I B lei A ID I c I BI c I BI A I A ID I c I
二、填空题〈本题共4小题,每小题5分,共20分〉
13. 2 14. 3 15. (-3,0)U(3,+oo) 16. 且,手),
三 、 简答题{本题共5小题, 每小题12分, 共60分}
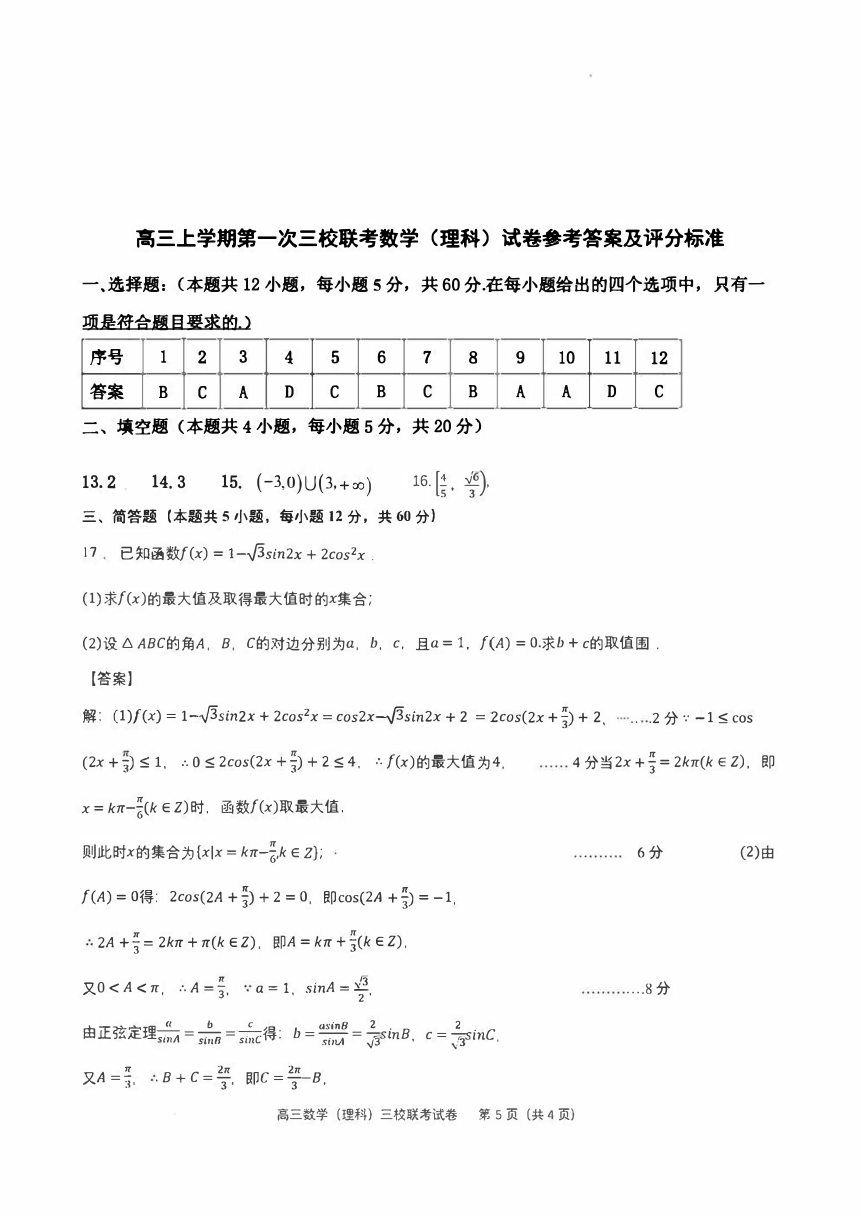
17 已知函数f(x) = 1-,/3sin2x + 2cos2x .
(1)求f(x)的最大值及取得最大值时的x集合J
(2)设 A ABC的角A, B, C的对边分别为α , b, c,且α= 1, f(A) = 0.求b+c的取值圈。
[答案]
解:(l)f(对= 1『,/3sin2川 2cos2x = cos2x刊3sin2x + 2 = 2cos(2x +争+ 2, .. .2 分 ·: -1 三 cos
π
(2x + 3)- 三 1, :. 0 三 2cos(2x + 3-) + 2 三 4, :. f(x)的最大值为 4. 4 分当2x+ = 2kπ(k ε Z) 即,
x=k -π Ick ε Z)时, 函数f(x)取最大值 ,
则此时x的集合为 {xlx=kπ-I.k εZ}; 6分 (2)由
f(A) = 0得: 2cos(2A + ) + 2 = 0 , 即cos(2A +号=-1.
2A +i= 2kπ + π(k ε Z), 目PA=kπ + (k ε Z).
又O由正弦定理力=:如=;二z:I导: b= 好=去=sinB, c =会叭
叉A 斗 .B+C=子 EIPC =子-8,, ,
高三数学(理科)三校联考试卷 第 5 页(共 4 页)
2 2 I 12π 飞|:. b + c = (sinB +s inC) = lsin8 + --::/3 --::j3 sin lτ
-8 JJ
=去(sinB +手cosB +卡inB) = 2(手sinB +争osB) = 2s附+ i), ... 10 分
·A = . . B ε (咛) , · 8 + E (i. f). 如(8 咔) εci.11.
贝ljb+c的取值范围为(1,2) .12分
18 如图 在三棱柱 ABC-A B,C 中 . 侧 面 AA,C,C, , ..1底 面 ABC1 , 侧 面 AA 1C1C是 菱 形 ,
L.A AC = 60., L.ACB = 90·. AC= BC= 2 c,
1
(1)若 D 为 A,C 的中点 求证’. AD .l A,B;
(2)求二面角 A-A,C-B 的正弦值。
,
[答案] (1)见解析 (2) 主 B
[详解] (1) ·:侧面AA ICIC是菱形 , :. AA, =AC.
·: D 为 .4ic的中点,二 AD ..l.4iC.
·.·侧面 A.4icp i底面 ABC ,似roo AA1c,cn底面 ABC=AC, L乙ACB=90。 , BC c底面 ABC,
BC .l侧面AA 1C1C.
·: AD c侧面AA 1C1C. :. BC .l AD.
·: A,cnsc=c. 二 AD..l 平面 A BC.I
·: A,B c平面 A BC ,二 AD..lA B ·····5 分
1 1
[2]取AiC1 中点 .连接 CE , 从而 CE ..lA,CI ’又由A 1C1 IIAC.则 C'E ..lAC,
·川则面 A.4icp i底面 ABC ,侧面AA1c1cn底面 ABC=AC,
:. CE .l底面 ABC.
以 C 为坐标原点 , 以 CA, CB. CE 为 x 轴,y轴 , z 轴建立空间直角坐标系,如下图
由己知条件和上图可知, C(O,0, 0), A(2, 0, 0). A (l, 0, Ji). B1 (-1, 2,占) ,i
由题意可知 平面AA C的一个法向量为 → ........ , 分I CB= 7( 0,2,0)
高三数学(理科)三校联考试卷 第6页(共4页)
c,
不妨设;=(矶,Yi,Z,)平面码CB 的一个法向量,
因为CA, = (l,O,J3) ’ CB, = (-l,2,J3)’
ICA二 ·ii=O =字」Ix,+、从而J t一二 ←/3z,
= 0
l 一
lCB ·月= 0, l-x +2y ..J3 =01 1 + z1
令 z, = J3 ,贝IJ x = -3. y = -3. 1 1 目p; = (-3,-3,J3), …9 分
设二面角 A-A1C-B1 为θ . 由图可知θ为钝角 ,
→ → _ I ’
从而 CB· n I _ l'J I 句J ?cos() = - I cos < CB, - -n >I一一了τ - 弓丰 , 目Psinθ=-工牛 ,
ICBllnl ’ 7
故二面角 A-A1C-B 的正弦值为2主 ··12分
,
7
19.某校组织围棋比赛 , 每场比赛采用五局三胜制(一方先胜三局即获胜 , 比赛结束) 比赛采用积分
制, 积分规则如下 每场比赛中 , 如果囚局及四局以内结束比赛 , 取胜的一方积3分 , 负者积0分, 五
局结束比我取胜的一方积 2 分 . 负者积 1 分已知甲乙两人脱 . 甲每局获胜的概率为÷
(1)在一场比赛中 , 甲的积分为 x 求 x 的概率分布列 ,
(2)求甲在参加三场比赛后积分之和为5分的概率
[答案] (1)见解析 (2)一一一333
2048
[详解] (1)由题意可知 , X可能取值为O, 1, 2, 3 ,
当 X=O 时 , 则前三场比赛都输或前三场比赛赢一场且第四场比赛输,
则 P(X =0) =( 1 - 一l),3 +C;, 一I ·(l I, I-一)2(1 --) = 5一 ,
2 , 2 2 2 16
当 X = l 时 , 前四场比赛赢两场且第五场比赛输 ,
则 = =C;, P(X I) ·(一I)。2 . (l - -l)。2 . (1 -一1 )=-3 ;
崎 2 2 2 16
当 X=2 时 , 前四场比赛赢两场且第五场比赛赢 ,
则 P(X = 2) = C!
、 ·(一l )2句 ·(1-一i )2。 .一1 =一3 ·
呼 2 2 2 16
当 X=3 时 , 前三场比赛都赢或前三场比赛赢两场且第四场比赛赢 ,
则 2P(X=3)=(一)3 ÷c;。 ·(一l )。2 (l -一l )一I = 5 一 ,
, 2 2 2 16
故x 的概率分布列如下
高三数学(理科)三校联考试卷 第7页(共4页)
x 。 1 2 3
5 3 3 5
16 16 16 16
····6分
[小问 2详解]设甲在参加三场比赛后 , 积分之和为5分为事件A,
则甲的三场比赛积分分别为 l 、 1、 3 或者0 、 2、 3 或者 1 、 2、 2,
故 = 3 3 5 A 3 · 5 3 5 · 3 3 3 333 P(A) 3 一·一·一+ 一-一·一+ 3 一·一-一=一一·
16 16 16 ' 16 16 16 16 16 16 2048
333
故甲在参加三场比赛后, 积分之和为5分为 -一- ........................ ,.,12分
2048
20. (12分〉己知刨C:你-1)2 +l=l , 椭圆M: ζ + L =I.
8 4
(I)求证:囱IC在椭圆M内:
(2)若因C的切线m与椭圆M交于 P, Q 两点 , F为椭圆M的右焦点 , 求A FPQ 面积的最大值 .
20. ( 12 分}
解:(I )副心C(l,O),半径,·=I.设 A(x.y) 为lllli阕M」工一点, ’’分
则 、IAC 「=(x-1),2 + y,' =(x-1},' +4--I , I I , ? .r' =士二, .,
' -2.r + 5 =τ(x-2)' +3. 9·, 分
._. -2.fi. x 2.fi.
.\二监 x=2时, JACJ有.Q小ffJ..J5 . ….......…·4分
而 .Jj > I,即JACJ川,放点A总在例C外 .
.· . 刨Ci!:椭阴IM内 . ……......... 5分
〈注:其他方法,合理正确均可得分〉
(2)若直线川斜率不存在,,, 不能过点F(2.的,贝。’”的方程只能为x=O.
I PQJ=4, =4. ….......…··7s..,咀 分
者应线m斜息存在.设刑的方程J】 y=kx+1, P(x,,y,), Q(x,,y,).
I k +1 J I I
曲直线,II与刨C相iJJ得 ' -τ =I,化衍得 I + 2 1 =I,则 k = ← - I),,笋0. ·········8分
.Jk'+I 21
[ x' y'
’
! 引m 言 4 得(2k2 + I)泸 + 4ktx+2t2 -8=0.
[y=kx+t
则 x. + λ 。 =兰k ι ,川=兰
二!_ ………
,
‘ I '
·9分
+ 2k‘ + I
A=( -4灿1)(2/1 咿“k2 -81 2 +3
J毕+812
JPQJ=Ji'百 Jx,-x,1 = ·丘ζι ’2k' F(2,0)茹lj m (l(J.W附h嘻 -刊 占可;
EEF-日
川 F M川U
设 s=t' +I,则 s> I,
sM ro = 王三?_=3JBI0l= ♂1<4 . BB 分I +I s 舍 V s' s
·. t::.FPQ 面积的极大li'l为4. 饨,- 分
21 (12 分)已知函数 f(x) = I .!_x2 - α·x I In x - .!_ x2 + ax
2 J
(l)若 f(x) 在(0, +oo)单调递增,求u的值:
I 3 f(x)
(2)当一〈α -< e 时,设函数 g(λ. )-_ 一一的最小值为 h(时,求函数 h(α)的值域.
4 4 x
’
解: (I) f 。) = (x-α) lnx.
’
因为 f(x) 在(0,+ >)单调递增,所以/ (x) 三 0 ,即 (x - α) lnx 兰 O
( i )当 x>l 时, lnx>O,则需 x-a 主 0 ,故 a 三x ’ fiPa 三l:
min
( ii )当 x= l 时, lnx=O,贝1Jaε R,
(iii)当 0< x < I 时, lnx综上述,α=I. 4分
g = f(x) -卜( l - J| l 刊 , _ l a l (x) 一一 ,g(x)-一 lnx 一 +一 ,g"(x) = 一 + 寸 ·因为
x 2 ) 4 2 x 4 2x x'
I 3
一
4 < a<-4 e,所以扩(
x) > 0,所以g ’(x) 在(O, +oo)单调递增
又因为g’
α3
(I)=-α+一 < O,g'(e) =-一 +一 >0.所以存在x0 E
’
(l,e ),使g (x0 )=0,
e 4
且当xε(0,x ’0 ) 时,g (x) < 0 ,函数 g(x) 单调即成:
当xε (x ,+oo)时,g’(x) > 0,函数 g(x) 调边j曾0
问明小值为忡。)=(1与才}叫
’ 1 ( 3 1 1 由g (x 一 一 -一0 ) = 0,得α=一~h与+ ~’囚此 hα( )=| Xo x Ir O ltn4 4 2 0 !
( J 1 1 令古 x) =-xlnx+-x,x E ’(I,吟,则 τ ( 3 x) =一lnx 一+ >0.2 4 2 4
J
所以 3 r(x)在区间(l,e )上单调递增,又回为一 < a<-e, !1.,(1 1 3 )=一 , r (e) =-e,
4 4 4 4
所以l < x0 < e , f.!I] x0 ij;(遍(1,功的每一个值,
令伊(x)=l(-3 x--l xlnx,Jl lnx(I I 2 J 0函
\4 2 ! 2 4 4 4
数ψ阳 M 单调递增 Y.. rp(川ψ(e)= ,所以0<仰)〈:-
攸函数 h
22 · ( 10 分) (选f1妻 4-4 :坐标系与参数方程l
lx=a + 主 t
在平面直角坐标 xOy 中,直线l的参数方程为↓ 2 ( I 为参数, 。 为常数)·以原点。为极点, xI
[Y = 2 t
轴正半轴为极轴建立瞅瞅,曲线 C的极姗姗为ρ=坐车手
sm-(f
(I)求直线l的普通方程和曲线C的直角坐标方程:
(2)设窒线/与仙线C相交于A、8两点,若IABl=I6,求α的俏.
--13 x- ---13 v a= "’ υ , a
(1) 3 3 . y 阳 : (2) a= l
lx=a+主 t
[详解l C I ) ·:直线l的参数方程为↓ 2 ( I 为参数,a为常数) ,J
[Y = /
消去参数I韧的普通方程为: y = 孚(卜。) nlix γ丑。= O. 2 分
.) 3
4cosθ
·.·ρ = --:---,-τ了, 二 ρsin
2 θ = 4cosθ 即 p2 sio 2 8=4ρcosθ , 即 y2 =4x.
SlOσ
=
故曲线C的直角坐标方程为y2 =4x. . ........5 分
C II )将直线l的参数方程代入曲线中得 2t -8-/3t-16a =0 , -……….. 7分
A =κυ 《 0 + 句J 、‘,J 〉 Aυ 20〉 。3
h + 8 JV I
’吃 士,3 AY 分
- = 「岭1 0
rzla1,dBEElt飞 ’叩2
2
|础 l=lt, -tzl 呐叫 ) -川而…= [. .10分
23 . [选修4-5;不等式选讲]
已知函数f(x) =Ix + α1+21x-ll.
(I )当=。= 2 时, 求不等式 f(x)至 4的解集;
(2)若:lxε[1,2] , 使得不等式 f(x)>x 2 成立 , 求实数a的取值范围
解:(1)当α=2时 , /(x)=lx+ 21+21x-ll.
当时 -2时 f(x) = -川 - 2x 山4 解得X主 - ; 此时XE0;
当-2当x>l时只x) =川山 - 2至 4 解得X三:此时 l因此当α= 2时不等式 f(x) 4的解制[o,1] 5分
(2)当 1豆 x豆2 肘 Ix + αI +21 x -11> x2, 可化为 Ix + αI> x2 -2x+2.
所以 x α x2 + >
, -2x+2 2 或 x+ a < -x + 2x -2
2 2
即存在 XE [1,2], 使得 α > x -3x+2 或 a<-x + x-2
。> x2 -3x + 2 = ( x -% ) 2 --l- . 因为阴阳所以川x 山 -i 则 α > -i,
,
。<-x2 + x - 2 = -( x -! y - 2'!_ . 因为民[川, 所以 -x +x-2 三 -2. 所以 a<-2,
2 J 4
(-oo,-2)UI -斗 +oo)
,
因此 , 实数a的取值范因为 \ 『 /
数学试卷〈理科〉
命题人z涂方珍 学校z南昌十中 考试时长: 120分钟 试卷总分: 150分
一、选择题: (本题共12小题, 每小题5分, 共60分.在每小题给出的四个选项中, 只有一
项是符合题目要求的.〉
l已知集合M十二子。)叫(| 升到)则MnN=C
A. [-4,-1] B.[-l,3) c.[-4,3) D. [-1,3]
2. 设平而向窒石, E均为单位!句蠢,贝I] “ 1ci-2E1 12ri + E1 ”是 "ri .L E”= 的〈 〉
A充分而不必要条件 B.必要而不充分条件
c. 充分必要条件 D.既不充分也不必要条件
3. 己知函数 f(x)=t''
x. 0, 则f(ln2) =
lf(x -1), x > 0
2
-4 A. 甲 B. C. 2e D. 4e
e
4 虫11 图,在 今 ABC中, BN = 扣,设五百 = a, Al斗,则五百=( )
A. 『 3- 3『 1- 1- 3- :i『 1-α--b - B. -a--b C . -a +-b D. -a +-b
4 4
5.如|望所示 . 在平面直角坐标系中 , 角α和角β均以 Ox 为始边. 终边分别为射线 OA和 OB , 射线 OA,
与单位圆的交点分别为Al(- 3
π
oc ,-4 11, C(-1,0) 着 LBOC = 一 , 贝ljcos(β- α)的值是(
5 5) 6
A. -叫
5 B. 3+4.jj
IO 10
I '1,('., I ,
c. 4-3
-fS
D. 4+3.jj
<:
IO 10
6通过研究正五边形和正十边形的作囚,古希腊数学家毕达哥拉斯发现了黄金分割率,黄金分割率的值也
‘反-I J石二骂王
可以归川
A. -2 B. -J2 c . .fi. o.Js-1
高三数学(理科)三校联考试卷 第1页(共4页)
7己知过点 A (α,0)作曲线 'y = (t-x)e 的切线有且仅有l条 , 贝归=〈 〉
A.-3 B.3 c.-3或1 D. 3或l
8己知何数f(明R上是增函数若α =-f(I咱i), b=f(l唱4.1), c=f(俨勺,则日, b, c的大小关系
为( )
A. a
A. 1t B.π c.2: o.I主
6 4 3 3
10.已知函数/(们{(气?当二飞\5'8,若数列{向}满足an = f(η)(nεN*)且{时是递晰列,则实数α的取
值?也图是( )
A. (2,3) B.(2,3) c.(!,3) D.[!,3)
π
11. 已知函数 f(x) = 2sin(x +伊)cosx-sinψ(|ψ|〈 -2 ) , 且对于任意x E R , 都有 't (x+-)=-f(--x). 下列3 3
ππ 、 J也 γ .11
序号中 , ① f(x) 在区间[-一6 ’-6 ]上单调递增’ ②/(0)=工
-
2 , ③着!( 2 )-丘 , 贝iJ f(xo -一12 )=一3 3 ,
④
4π
着实数m使得为程 f(x)-m = 。在(0,τ)上恰有与·勺 , 以X1
x 口+、,& x +x -π 的
3 正 确 序亏有
A①②③ B.①③④ c. ①②④ D.②③④
12.黎曼函数 R(x)是一个特殊函数 . 由德国数学家黎曼发现并提出 , 该函数定义在(0, 1)上 . 当x =!巾q,
都是正整数,:为最俏真分数)时,R(们 i;当x=O或1或x为CO, 1)内的无理数毗 R(x) = 0.若9
(x + 1)1'1偶 l苟 敛, g(x + 2);但奇民数,当xε(0,1)时, g(x) = R(x) 则, (
A.g(平)>抖 (cos2创川的主 g(cos2圳(呻)
(平)>i且g(co内呻)三 g(cos2B.g 彻(的)
C.g(平)=如(cos2阳印)三 g(co泸α)g(si
D.g(平)=i g(cos2且 asi训)三 g(c的)仰in2{3)
二、填空题(本题共 4 小题, 每小题 5 分, 共 20 分〉
高三数学(理科)三校联考试卷 第2页(共4页)
13 已知aeR若复数z = a2-a-2 + (α2 +3α + 2)i为纯虚数 , 贝1Ja = 一一一一一一
14.如图 , 扇环ABCD 巾,弧AD=4,弧ic = 2, IABI = 1co1 = 1,
Yrn扇1不ABCD的面积S = ·
一一一一 ·(;二〉
15 已知函数 f(x) 是定义域为 R 的奇函数 . 当 x>O 时 ’, / (-x) > 2/(x) , 且 f(3)=0 , 则不等式
f(x)>O 的解的一一一
16.锐角A ABC中 , α , b, c为角A, B, C所对的边 , 点C为A ABC的重心 , 若AG .l BG,则cosC的取值范
图为
三、简答题〈本题共 5 小题,每小题 12 分,共 60 分〉
l 7 . (12 分)已知函数f(x) = 1-J'Jsin2x + 2cos与
(1)求f(x)的最大值及取得最大值的的x集合J
(2)设A ABC的角A, B, C的对边分别为α , b, c , 且α= 1, f(A) = 0求. b+c的取值范围
18. (12分)如图,在三棱柱 ABC-A1 B1C1 中,侧面AA I C ,IC .L底面AβC 侧面AA CC是菱形 ,1 1
LA AC = 60'「 . ζA CB=90° , AC=BC=2I
c,
(1 )若D为A C的中点 , 求证: AD.LA
1 I B;
2( )求二面角 A-A1C-B1 的正弦僵
B
19. 1( 2分)某校组织围棋比赛, 每场比赛采用五局三胜制( 一方先胜三局即获胜 , 比赛结束)、 比赛采
用积分制 , 积分规则如下 每场比赛中 , 如果四局及四局以内结束比赛 , 取胜的一方积 3 分. 负者积 0
分j五局结束比赛 . 取胜的一方积2分负者积1分已知甲乙丙人比赛 . 甲每局获胜的概率 为士
(1 )在一场比赛中 , 甲的积分为X, 求X的概率分布列 ,
高三数学(理科)三校联考试卷 第3页(共4页)
(2)求甲在参加三场比赛后 , 积分之和为5分的概率
20 (12分)己知困C: (x -1)2 + 2 y = l 椭圆M 王: + 丘, = l .
8 4
( l)求-liE:因 ctt椭圆M内:
(2)若因C的切J线m与椭圆 M 交于 P, Q 两点 , F为椭圆M伯右焦点 , 求A FPQ 丽积的最大值 .
21时)已知函数f叫i~) tox 卡叫
(l)若 f(x) 在(O,+oo)单调递增 , 求。的值.
I 3
(2)当-<α x< - e 时 , 设函数 g(x)-_ f( ) 一一- 的:最小值为h(α) , 求函数 h(α)的值城 .
4 4 x
四、选{故题
22 ( 10分)[选修4.4: 坐标系与参数为程]
lI x=a.+-.J3 二-t
在平商直角坐标x0,中 , 直线l的参数方程为{I 2 (I 为参数, 。 为常数) 以原点。为极点, x
l
I v=-t
L 2
4cosθ
轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ= --:-:;-::-
sm 11
(1 )求直线l的普通方程和lffi线C的直角坐标方程:
(2)设直线l与曲线C相交于 A,B 网点 , 若IABI = 16 , 求。 的值.
23 (10分)[选修4-5: 不等式选讲 l
已知函数f(x) =Ix+αl+2lx-lj.
( l)当α=2时 , 求不等式 f(x) 至4的解集j
(2)若 3x E (1,2) , 使得不等式 f(x) >川成立 , 求实数。的取值范围。
高三数学(理科)三校联考试卷 第4页(共4页)
高三上学期第-次三校联考数学(理科〉试卷参考答案及评分标准
一、选择题: (本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的. 〉
|序号I 1 I2 I 3 I 4 I s I 6 I 1 I s I 9 I 10 I 11 I 12 I
|答案I B lei A ID I c I BI c I BI A I A ID I c I
二、填空题〈本题共4小题,每小题5分,共20分〉
13. 2 14. 3 15. (-3,0)U(3,+oo) 16. 且,手),
三 、 简答题{本题共5小题, 每小题12分, 共60分}
17 已知函数f(x) = 1-,/3sin2x + 2cos2x .
(1)求f(x)的最大值及取得最大值时的x集合J
(2)设 A ABC的角A, B, C的对边分别为α , b, c,且α= 1, f(A) = 0.求b+c的取值圈。
[答案]
解:(l)f(对= 1『,/3sin2川 2cos2x = cos2x刊3sin2x + 2 = 2cos(2x +争+ 2, .. .2 分 ·: -1 三 cos
π
(2x + 3)- 三 1, :. 0 三 2cos(2x + 3-) + 2 三 4, :. f(x)的最大值为 4. 4 分当2x+ = 2kπ(k ε Z) 即,
x=k -π Ick ε Z)时, 函数f(x)取最大值 ,
则此时x的集合为 {xlx=kπ-I.k εZ}; 6分 (2)由
f(A) = 0得: 2cos(2A + ) + 2 = 0 , 即cos(2A +号=-1.
2A +i= 2kπ + π(k ε Z), 目PA=kπ + (k ε Z).
又O
叉A 斗 .B+C=子 EIPC =子-8,, ,
高三数学(理科)三校联考试卷 第 5 页(共 4 页)
2 2 I 12π 飞|:. b + c = (sinB +s inC) = lsin8 + --::/3 --::j3 sin lτ
-8 JJ
=去(sinB +手cosB +卡inB) = 2(手sinB +争osB) = 2s附+ i), ... 10 分
·A = . . B ε (咛) , · 8 + E (i. f). 如(8 咔) εci.11.
贝ljb+c的取值范围为(1,2) .12分
18 如图 在三棱柱 ABC-A B,C 中 . 侧 面 AA,C,C, , ..1底 面 ABC1 , 侧 面 AA 1C1C是 菱 形 ,
L.A AC = 60., L.ACB = 90·. AC= BC= 2 c,
1
(1)若 D 为 A,C 的中点 求证’. AD .l A,B;
(2)求二面角 A-A,C-B 的正弦值。
,
[答案] (1)见解析 (2) 主 B
[详解] (1) ·:侧面AA ICIC是菱形 , :. AA, =AC.
·: D 为 .4ic的中点,二 AD ..l.4iC.
·.·侧面 A.4icp i底面 ABC ,似roo AA1c,cn底面 ABC=AC, L乙ACB=90。 , BC c底面 ABC,
BC .l侧面AA 1C1C.
·: AD c侧面AA 1C1C. :. BC .l AD.
·: A,cnsc=c. 二 AD..l 平面 A BC.I
·: A,B c平面 A BC ,二 AD..lA B ·····5 分
1 1
[2]取AiC1 中点 .连接 CE , 从而 CE ..lA,CI ’又由A 1C1 IIAC.则 C'E ..lAC,
·川则面 A.4icp i底面 ABC ,侧面AA1c1cn底面 ABC=AC,
:. CE .l底面 ABC.
以 C 为坐标原点 , 以 CA, CB. CE 为 x 轴,y轴 , z 轴建立空间直角坐标系,如下图
由己知条件和上图可知, C(O,0, 0), A(2, 0, 0). A (l, 0, Ji). B1 (-1, 2,占) ,i
由题意可知 平面AA C的一个法向量为 → ........ , 分I CB= 7( 0,2,0)
高三数学(理科)三校联考试卷 第6页(共4页)
c,
不妨设;=(矶,Yi,Z,)平面码CB 的一个法向量,
因为CA, = (l,O,J3) ’ CB, = (-l,2,J3)’
ICA二 ·ii=O =字」Ix,+、从而J t一二 ←/3z,
= 0
l 一
lCB ·月= 0, l-x +2y ..J3 =01 1 + z1
令 z, = J3 ,贝IJ x = -3. y = -3. 1 1 目p; = (-3,-3,J3), …9 分
设二面角 A-A1C-B1 为θ . 由图可知θ为钝角 ,
→ → _ I ’
从而 CB· n I _ l'J I 句J ?cos() = - I cos < CB, - -n >I一一了τ - 弓丰 , 目Psinθ=-工牛 ,
ICBllnl ’ 7
故二面角 A-A1C-B 的正弦值为2主 ··12分
,
7
19.某校组织围棋比赛 , 每场比赛采用五局三胜制(一方先胜三局即获胜 , 比赛结束) 比赛采用积分
制, 积分规则如下 每场比赛中 , 如果囚局及四局以内结束比赛 , 取胜的一方积3分 , 负者积0分, 五
局结束比我取胜的一方积 2 分 . 负者积 1 分已知甲乙两人脱 . 甲每局获胜的概率为÷
(1)在一场比赛中 , 甲的积分为 x 求 x 的概率分布列 ,
(2)求甲在参加三场比赛后积分之和为5分的概率
[答案] (1)见解析 (2)一一一333
2048
[详解] (1)由题意可知 , X可能取值为O, 1, 2, 3 ,
当 X=O 时 , 则前三场比赛都输或前三场比赛赢一场且第四场比赛输,
则 P(X =0) =( 1 - 一l),3 +C;, 一I ·(l I, I-一)2(1 --) = 5一 ,
2 , 2 2 2 16
当 X = l 时 , 前四场比赛赢两场且第五场比赛输 ,
则 = =C;, P(X I) ·(一I)。2 . (l - -l)。2 . (1 -一1 )=-3 ;
崎 2 2 2 16
当 X=2 时 , 前四场比赛赢两场且第五场比赛赢 ,
则 P(X = 2) = C!
、 ·(一l )2句 ·(1-一i )2。 .一1 =一3 ·
呼 2 2 2 16
当 X=3 时 , 前三场比赛都赢或前三场比赛赢两场且第四场比赛赢 ,
则 2P(X=3)=(一)3 ÷c;。 ·(一l )。2 (l -一l )一I = 5 一 ,
, 2 2 2 16
故x 的概率分布列如下
高三数学(理科)三校联考试卷 第7页(共4页)
x 。 1 2 3
5 3 3 5
16 16 16 16
····6分
[小问 2详解]设甲在参加三场比赛后 , 积分之和为5分为事件A,
则甲的三场比赛积分分别为 l 、 1、 3 或者0 、 2、 3 或者 1 、 2、 2,
故 = 3 3 5 A 3 · 5 3 5 · 3 3 3 333 P(A) 3 一·一·一+ 一-一·一+ 3 一·一-一=一一·
16 16 16 ' 16 16 16 16 16 16 2048
333
故甲在参加三场比赛后, 积分之和为5分为 -一- ........................ ,.,12分
2048
20. (12分〉己知刨C:你-1)2 +l=l , 椭圆M: ζ + L =I.
8 4
(I)求证:囱IC在椭圆M内:
(2)若因C的切线m与椭圆M交于 P, Q 两点 , F为椭圆M的右焦点 , 求A FPQ 面积的最大值 .
20. ( 12 分}
解:(I )副心C(l,O),半径,·=I.设 A(x.y) 为lllli阕M」工一点, ’’分
则 、IAC 「=(x-1),2 + y,' =(x-1},' +4--I , I I , ? .r' =士二, .,
' -2.r + 5 =τ(x-2)' +3. 9·, 分
._. -2.fi. x 2.fi.
.\二监 x=2时, JACJ有.Q小ffJ..J5 . ….......…·4分
而 .Jj > I,即JACJ川,放点A总在例C外 .
.· . 刨Ci!:椭阴IM内 . ……......... 5分
〈注:其他方法,合理正确均可得分〉
(2)若直线川斜率不存在,,, 不能过点F(2.的,贝。’”的方程只能为x=O.
I PQJ=4, =4. ….......…··7s..,咀 分
者应线m斜息存在.设刑的方程J】 y=kx+1, P(x,,y,), Q(x,,y,).
I k +1 J I I
曲直线,II与刨C相iJJ得 ' -τ =I,化衍得 I + 2 1 =I,则 k = ← - I),,笋0. ·········8分
.Jk'+I 21
[ x' y'
’
! 引m 言 4 得(2k2 + I)泸 + 4ktx+2t2 -8=0.
[y=kx+t
则 x. + λ 。 =兰k ι ,川=兰
二!_ ………
,
‘ I '
·9分
+ 2k‘ + I
A=( -4灿1)(2/1 咿“k2 -81 2 +3
J毕+812
JPQJ=Ji'百 Jx,-x,1 = ·丘ζι ’2k' F(2,0)茹lj m (l(J.W附h嘻 -刊 占可;
EEF-日
川 F M川U
设 s=t' +I,则 s> I,
sM ro = 王三?_=3JBI0l= ♂1<4 . BB 分I +I s 舍 V s' s
·. t::.FPQ 面积的极大li'l为4. 饨,- 分
21 (12 分)已知函数 f(x) = I .!_x2 - α·x I In x - .!_ x2 + ax
2 J
(l)若 f(x) 在(0, +oo)单调递增,求u的值:
I 3 f(x)
(2)当一〈α -< e 时,设函数 g(λ. )-_ 一一的最小值为 h(时,求函数 h(α)的值域.
4 4 x
’
解: (I) f 。) = (x-α) lnx.
’
因为 f(x) 在(0,+ >)单调递增,所以/ (x) 三 0 ,即 (x - α) lnx 兰 O
( i )当 x>l 时, lnx>O,则需 x-a 主 0 ,故 a 三x ’ fiPa 三l:
min
( ii )当 x= l 时, lnx=O,贝1Jaε R,
(iii)当 0< x < I 时, lnx
g = f(x) -卜( l - J| l 刊 , _ l a l (x) 一一 ,g(x)-一 lnx 一 +一 ,g"(x) = 一 + 寸 ·因为
x 2 ) 4 2 x 4 2x x'
I 3
一
4 < a<-4 e,所以扩(
x) > 0,所以g ’(x) 在(O, +oo)单调递增
又因为g’
α3
(I)=-α+一 < O,g'(e) =-一 +一 >0.所以存在x0 E
’
(l,e ),使g (x0 )=0,
e 4
且当xε(0,x ’0 ) 时,g (x) < 0 ,函数 g(x) 单调即成:
当xε (x ,+oo)时,g’(x) > 0,函数 g(x) 调边j曾0
问明小值为忡。)=(1与才}叫
’ 1 ( 3 1 1 由g (x 一 一 -一0 ) = 0,得α=一~h与+ ~’囚此 hα( )=| Xo x Ir O ltn4 4 2 0 !
( J 1 1 令古 x) =-xlnx+-x,x E ’(I,吟,则 τ ( 3 x) =一lnx 一+ >0.2 4 2 4
J
所以 3 r(x)在区间(l,e )上单调递增,又回为一 < a<-e, !1.,(1 1 3 )=一 , r (e) =-e,
4 4 4 4
所以l < x0 < e , f.!I] x0 ij;(遍(1,功的每一个值,
令伊(x)=l(-3 x--l xlnx,Jl lnx(I I 2 J
\4 2 ! 2 4 4 4
数ψ阳 M 单调递增 Y.. rp(川ψ(e)= ,所以0<仰)〈:-
攸函数 h
22 · ( 10 分) (选f1妻 4-4 :坐标系与参数方程l
lx=a + 主 t
在平面直角坐标 xOy 中,直线l的参数方程为↓ 2 ( I 为参数, 。 为常数)·以原点。为极点, xI
[Y = 2 t
轴正半轴为极轴建立瞅瞅,曲线 C的极姗姗为ρ=坐车手
sm-(f
(I)求直线l的普通方程和曲线C的直角坐标方程:
(2)设窒线/与仙线C相交于A、8两点,若IABl=I6,求α的俏.
--13 x- ---13 v a= "’ υ , a
(1) 3 3 . y 阳 : (2) a= l
lx=a+主 t
[详解l C I ) ·:直线l的参数方程为↓ 2 ( I 为参数,a为常数) ,J
[Y = /
消去参数I韧的普通方程为: y = 孚(卜。) nlix γ丑。= O. 2 分
.) 3
4cosθ
·.·ρ = --:---,-τ了, 二 ρsin
2 θ = 4cosθ 即 p2 sio 2 8=4ρcosθ , 即 y2 =4x.
SlOσ
=
故曲线C的直角坐标方程为y2 =4x. . ........5 分
C II )将直线l的参数方程代入曲线中得 2t -8-/3t-16a =0 , -……….. 7分
A =κυ 《 0 + 句J 、‘,J 〉 Aυ 20〉 。3
h + 8 JV I
’吃 士,3 AY 分
- = 「岭1 0
rzla1,dBEElt飞 ’叩2
2
|础 l=lt, -tzl 呐叫 ) -川而…= [. .10分
23 . [选修4-5;不等式选讲]
已知函数f(x) =Ix + α1+21x-ll.
(I )当=。= 2 时, 求不等式 f(x)至 4的解集;
(2)若:lxε[1,2] , 使得不等式 f(x)>x 2 成立 , 求实数a的取值范围
解:(1)当α=2时 , /(x)=lx+ 21+21x-ll.
当时 -2时 f(x) = -川 - 2x 山4 解得X主 - ; 此时XE0;
当-2
(2)当 1豆 x豆2 肘 Ix + αI +21 x -11> x2, 可化为 Ix + αI> x2 -2x+2.
所以 x α x2 + >
, -2x+2 2 或 x+ a < -x + 2x -2
2 2
即存在 XE [1,2], 使得 α > x -3x+2 或 a<-x + x-2
。> x2 -3x + 2 = ( x -% ) 2 --l- . 因为阴阳所以川x 山 -i 则 α > -i,
,
。<-x2 + x - 2 = -( x -! y - 2'!_ . 因为民[川, 所以 -x +x-2 三 -2. 所以 a<-2,
2 J 4
(-oo,-2)UI -斗 +oo)
,
因此 , 实数a的取值范因为 \ 『 /
同课章节目录
