人教B版高中数学选择性必修第一册《2.2两条直线的位置关系》名师课件(共31张PPT)
文档属性
| 名称 | 人教B版高中数学选择性必修第一册《2.2两条直线的位置关系》名师课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 21:54:29 | ||
图片预览








文档简介
(共31张PPT)
复习引入
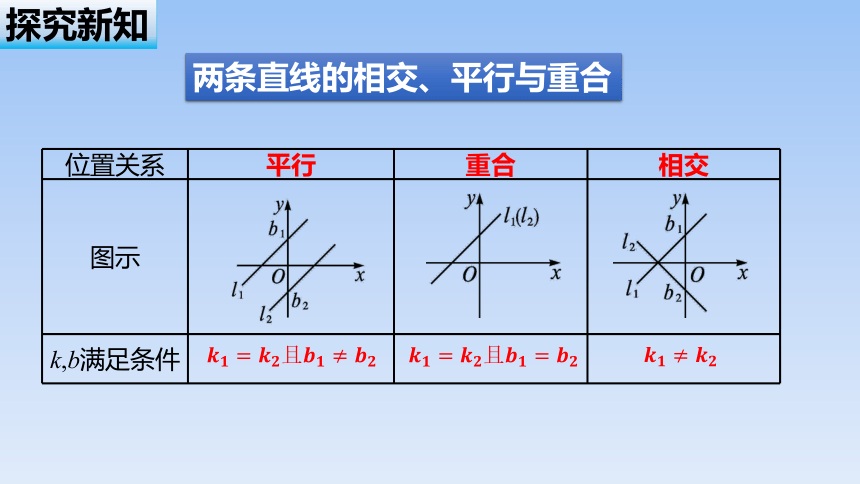
直线的方程
点斜式:
斜截式:
截距式:
一般式:
人教B版同步教材名师课件
两条直线的位置关系
学习目标
学 习 目 标 核心素养
理解并掌握两条直线平行的条件及两条直线垂直的条件 数学抽象
掌握利用解方程组求两条直线的交点坐标的方法 数学运算
学习目标
学习目标:
1.理解通过方程组给出的两条直线相交、平行、重合的条件.
2.能根据已知条件判断两直线的平行与垂直.
3.能应用两条直线的平行或垂直解决实际问题.
学科核心素养:
通过对两条直线平行与垂直的学习,提升直观想象、逻辑推理和数学运算的数学素养.
探究新知
若两直线的斜率均存在,我们可以利用斜率和在轴上的截距判断两直线的位置关系,其方法如下:
设
两条直线的相交、平行与重合
1.几何方法判断
探究新知
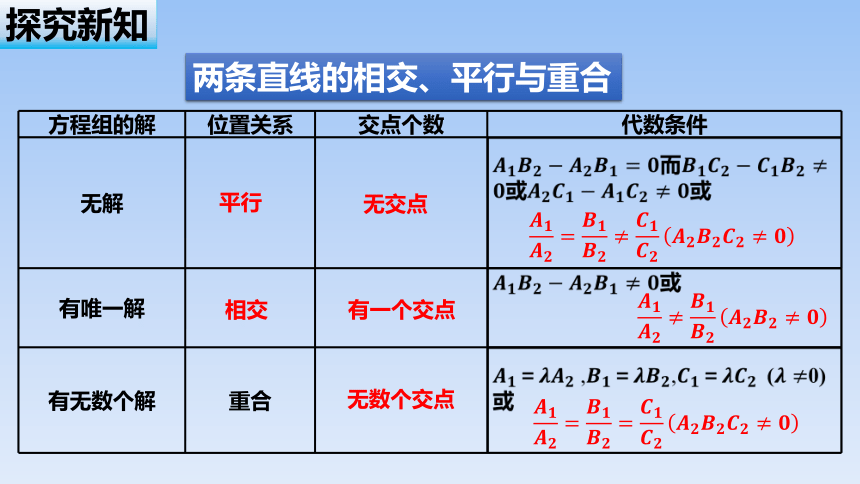
位置关系 平行 重合 相交
图示
k,b满足条件
两条直线的相交、平行与重合
探究新知
两条直线的位置关系,可以用方程组的解进行判断(如下表所示)
两条直线的相交、平行与重合
2.代数法判断
探究新知
方程组的解 位置关系 交点个数 代数条件
无解
有唯一解
有无数个解 重合
两条直线的相交、平行与重合
平行
无交点
相交
有一个交点
无数个交点
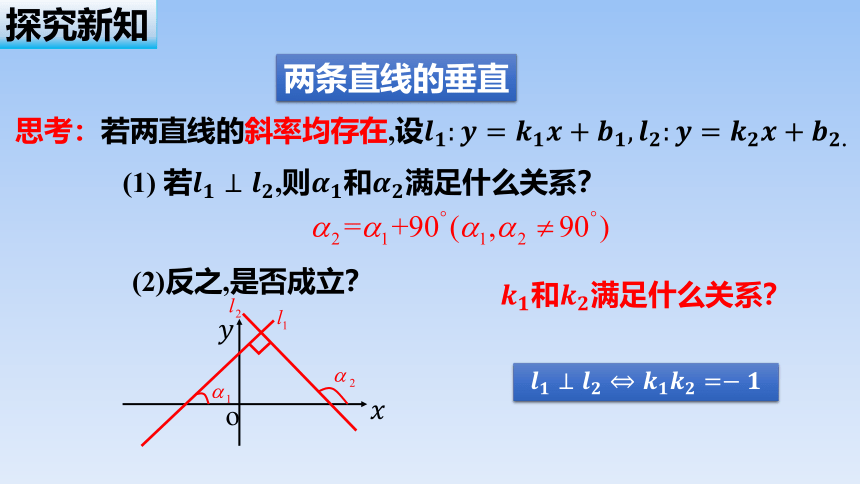
(2)反之,是否成立?
o
探究新知
思考:若两直线的斜率均存在,设.
(1) 若,则和满足什么关系?
满足什么关系?
两条直线的垂直
o
探究新知
思考:若直线垂直,我们该怎么样去判断它们是否垂直呢?
是直线的一个法向量,
是直线的一个法向量
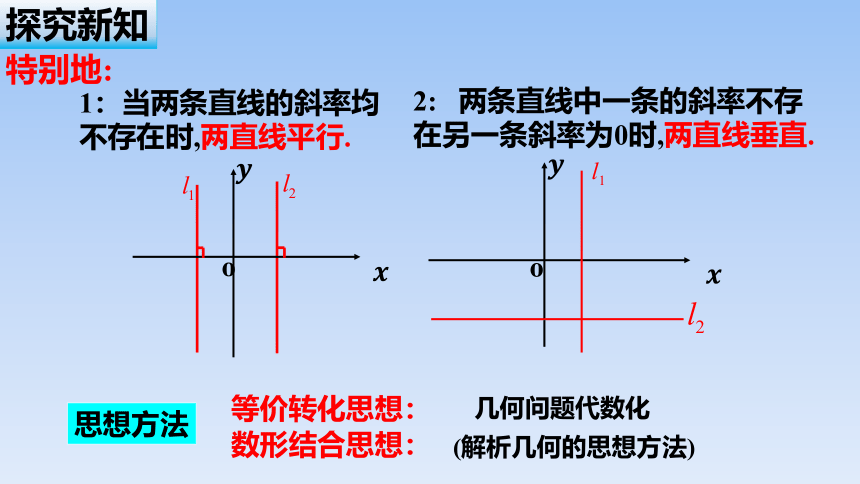
1:当两条直线的斜率均不存在时,两直线平行.
o
特别地:
o
2: 两条直线中一条的斜率不存在另一条斜率为0时,两直线垂直.
等价转化思想:
(解析几何的思想方法)
数形结合思想:
几何问题代数化
思想方法
探究新知
C
典例讲解
(2)根据下列给定的条件,判断直线与直线是否平行:
①经过点经过点,;
②的倾斜角为60°,经过点,;
③平行于轴, 经过点;
④经过点经过点.
例1、(1)直线的斜率,直线经过点, ,则的值为( )
解析
(1)因为的斜率且,所以,即,所以.
(2)①由题意知,, ,因为,且四点不共线,所以.
②由题意知, , ,因为, 所以或重合.
C
典例讲解
(2)根据下列给定的条件,判断直线与直线是否平行:
①经过点经过点,;
②的倾斜角为60°,经过点,;
③平行于轴, 经过点;
④经过点经过点.
例1、(1)直线的斜率,直线经过点, ,则的值为( )
解析
(2)③由题意知, 的斜率不存在,且不是轴, 的斜率也不存在,恰好是轴.所以.
④由题意知,, ,虽然,但是四点共线,所以重合.
例2、判断下列各小题中的直线l1与l2是否平行:
(1)l1经过点A(-1,-2),B(2,1),l2经过点M(3,4),N(-1,-1);
(2)l1的斜率为1,l2经过点A(1,1),B(2,2);
(3)l1经过点A(0,1),B(1,0),l2经过点M(-1,3),N(2,0);
(4)l1经过点A(-3,2),B(-3,10),l2经过点M(5,-2),N(5,5).
典例讲解
(1), ,, 不平行.
(2) , ,, 故或重合.
(3) , ,则有, 又, 则不共线.故
(4)由已知点的坐标,得均与轴垂直且不重合,故有
解析
(1)判断两条直线平行,应首先看两条直线的斜率是否存在,即先看两点的横坐标是否相等,对于横坐标相等是特殊情况,应特殊判断.再证明两条直线平行时,要区分平行与重合,必须强调不共线才能确定平行.因为斜率相等也可以推出两条直线重合.
(2)应用两条直线平行求参数值时,应分斜率存在与不存在两种情况求解.
方法归纳
变式训练
(1)由题意知方程2x2-4x+m-1=0的两实根相等,所以Δ=(-4)2-4×2×(m-1)=0.解之得m=3.
1.(1)已知两平行直线的斜率是方程2x2-4x+m-1=0的两实根,则m的值为( )
A.1 B.-1 C.3 D.-3
(2)已知P(-2,m),Q(m,4),M(m+2,3),N(1,1),若直线PQ∥直线MN,求m的值.
解析
C
(2)当时,直线PQ的斜率不存在,而直线MN的斜率存在,MN与PQ不平行,不合题意;
当时,直线MN的斜率不存在,而直线PQ的斜率存在,MN与PQ不平行,不合题意;
当且时,kPQ== , kMN== .
变式训练
1.(1)已知两平行直线的斜率是方程2x2-4x+m-1=0的两实根,则m的值为( )
A.1 B.-1 C.3 D.-3
(2)已知P(-2,m),Q(m,4),M(m+2,3),N(1,1),若直线PQ∥直线MN,求m的值.
解析
C
因为直线PQ∥直线MN,所以kPQ=kMN,即,解得m=0或m=1.
当m=0或1时,由图形知,两直线不重合.
综上,m的值为0或1.
典例讲解
例3、(1)直线l1经过点A(3,2),B(3,-1),直线l2经过点M(1,1),N(2,1),判断l1与l2是否垂直;
(2)已知直线l1经过点A(3,a),B(a-2,3),直线l2经过点C(2,3),D(-1,a-2),若l1⊥l2,求a的值.
(1)直线l1的斜率不存在,直线l2的斜率为0,所以l1⊥l2.
(2)由题意,知直线l2的斜率k2一定存在,直线l1的斜率可能不存在.
当直线l1的斜率不存在时,3=a-2,即a=5,此时k2=0,则l1⊥l2,满足题意.
当直线的斜率存在时,, .由,知,即×,解得.综上所述, 的值为0或5.
解析
(1)若斜率存在,求出斜率,利用垂直的条件判断;若斜率不存在,可结合图形判断.
(2)当两直线的斜率都存在时,由斜率之积等于-1求解;若一条直线的斜率不存在,由另一条直线的斜率为0求解.
(3)计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式时要对参数进行讨论.
方法归纳
变式训练
2.直线l1,l2的斜率是方程x2-2021x-1=0的两实根,则l1与l2的关系是__________.
Δ=(-2 021)2-4×1×(-1)=2 0212+4>0,x1x2=-1.即l1、l2的斜率之积k1k2=-1. 所以l1⊥l2.
l1⊥l2
解析
例4、如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5 m,宽AB=3 m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?
典例讲解
由AD=5 m,AB=3 m,可得C(5,0),D(5,3),A(0,3).设点M的坐标为(x,0),因为AC⊥DM,所以kAC·kDM=-1.所以× =-1,即x= =3.2,
即当BM=3.2 m时,两条小路AC与DM相互垂直.
解析
如图,以点B为坐标原点,BC,BA所在直线分别为x轴,y轴建立直角坐标系.
(1)建立恰当的直角坐标系;
(2)将“形”转化为“数”进行运算;
(3)将计算结果转化为实际问题中的所求解问题.
利用坐标法解决实际问题的三个步骤
方法归纳
变式训练
3.已知A(2,2+2),B(-2,2),C(0,2-2 ),D(4,2)四个点,顺次连接这四点,试判断四边形ABCD的形状.(说明理由)
因为kAB= = ,kBC= =-,
kAD= =- ,kCD= = ,所以kAB=kCD,kBC=kAD.
所以AB∥CD且BC∥AD,所以四边形是平行四边形,
解析
又因为,所以⊥,所以四边形是矩形.
又因为,,,
所以四边形不是正方形,所以四边形是矩形
(1)当直线l1∥直线l2时,可能它们的斜率都存在且相等,也可能斜率都不存在.
(2)直线l1,l2的斜率分别为k1,k2,当k1=k2时,l1∥l2或l1与l2重合.
(3)对于不重合的直线l1,l2,其倾斜角分别为α,β,有l1∥l2 α=β.
素养提炼
理解两条直线平行与斜率之间的关系
(1)利用l1⊥l2 k1·k2=-1,判断两条直线垂直的前提是这两条直线的斜率都存在,且都不为0.
(2)如果k1·k2≠-1,则这两条直线一定不会垂直.
(3)若两条直线中,一条直线斜率不存在,同时另一条直线斜率等于零,则这两条直线垂直.
这样,两条直线垂直的判定的条件就可叙述为:l1⊥l2 k1·k2=-1或一条直线斜率不存在,同时另一条直线斜率等于零.
素养提炼
理解两条直线垂直与斜率之间的关系
用坐标法研究数学问题是指在平面直角坐标系的基础上,
用坐标表示点,用方程表示曲线,通过对坐标和方程的代数化处理,
来解决平面图形的性质或平面图形中一些位置关系的判定.
素养提炼
坐标法解决数学问题的指导思想
当堂练习
解析
1.已知A(2,0),B(3,3),直线l∥AB,则直线l的斜率k等于( )
A.-3 B.3 C.- D.
B
因为直线l ∥AB,所以
2.若经过点(3,a)、(-2,0)的直线与经过点(3,-4)且斜率为的直线垂直,则a的值为( )
A. B. C.10 D.-10
D
解析
当堂练习
3.若不同两点P、Q的坐标分别为(a,b),(3-b,3-a),则线段PQ的垂直平分线的斜率为________.
由两点的斜率公式可得:,所以线段PQ的垂直平分线的斜率为-1.
-1
解析
4.已知点A(1,2)和点B(0,0),点P在y轴上,若∠BAP为直角,则点P的坐标为________.
设P(0,y),因为∠BAP为直角,所以kAB·kAP=-1,即,解得.
解析
当堂练习
5.已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,试求点D的坐标.
设D(x,y),
∵AB⊥CD且AD∥BC,
.
解析
归纳小结
两直线的位置关系
平行
重合
相交
斜截式方程的判定
一般式方程的判定
垂直
斜截式方程的判定
一般式方程的判定
交点坐标
作 业
课本P91页练习第1,4题
P92页练习第2,6题
复习引入
直线的方程
点斜式:
斜截式:
截距式:
一般式:
人教B版同步教材名师课件
两条直线的位置关系
学习目标
学 习 目 标 核心素养
理解并掌握两条直线平行的条件及两条直线垂直的条件 数学抽象
掌握利用解方程组求两条直线的交点坐标的方法 数学运算
学习目标
学习目标:
1.理解通过方程组给出的两条直线相交、平行、重合的条件.
2.能根据已知条件判断两直线的平行与垂直.
3.能应用两条直线的平行或垂直解决实际问题.
学科核心素养:
通过对两条直线平行与垂直的学习,提升直观想象、逻辑推理和数学运算的数学素养.
探究新知
若两直线的斜率均存在,我们可以利用斜率和在轴上的截距判断两直线的位置关系,其方法如下:
设
两条直线的相交、平行与重合
1.几何方法判断
探究新知
位置关系 平行 重合 相交
图示
k,b满足条件
两条直线的相交、平行与重合
探究新知
两条直线的位置关系,可以用方程组的解进行判断(如下表所示)
两条直线的相交、平行与重合
2.代数法判断
探究新知
方程组的解 位置关系 交点个数 代数条件
无解
有唯一解
有无数个解 重合
两条直线的相交、平行与重合
平行
无交点
相交
有一个交点
无数个交点
(2)反之,是否成立?
o
探究新知
思考:若两直线的斜率均存在,设.
(1) 若,则和满足什么关系?
满足什么关系?
两条直线的垂直
o
探究新知
思考:若直线垂直,我们该怎么样去判断它们是否垂直呢?
是直线的一个法向量,
是直线的一个法向量
1:当两条直线的斜率均不存在时,两直线平行.
o
特别地:
o
2: 两条直线中一条的斜率不存在另一条斜率为0时,两直线垂直.
等价转化思想:
(解析几何的思想方法)
数形结合思想:
几何问题代数化
思想方法
探究新知
C
典例讲解
(2)根据下列给定的条件,判断直线与直线是否平行:
①经过点经过点,;
②的倾斜角为60°,经过点,;
③平行于轴, 经过点;
④经过点经过点.
例1、(1)直线的斜率,直线经过点, ,则的值为( )
解析
(1)因为的斜率且,所以,即,所以.
(2)①由题意知,, ,因为,且四点不共线,所以.
②由题意知, , ,因为, 所以或重合.
C
典例讲解
(2)根据下列给定的条件,判断直线与直线是否平行:
①经过点经过点,;
②的倾斜角为60°,经过点,;
③平行于轴, 经过点;
④经过点经过点.
例1、(1)直线的斜率,直线经过点, ,则的值为( )
解析
(2)③由题意知, 的斜率不存在,且不是轴, 的斜率也不存在,恰好是轴.所以.
④由题意知,, ,虽然,但是四点共线,所以重合.
例2、判断下列各小题中的直线l1与l2是否平行:
(1)l1经过点A(-1,-2),B(2,1),l2经过点M(3,4),N(-1,-1);
(2)l1的斜率为1,l2经过点A(1,1),B(2,2);
(3)l1经过点A(0,1),B(1,0),l2经过点M(-1,3),N(2,0);
(4)l1经过点A(-3,2),B(-3,10),l2经过点M(5,-2),N(5,5).
典例讲解
(1), ,, 不平行.
(2) , ,, 故或重合.
(3) , ,则有, 又, 则不共线.故
(4)由已知点的坐标,得均与轴垂直且不重合,故有
解析
(1)判断两条直线平行,应首先看两条直线的斜率是否存在,即先看两点的横坐标是否相等,对于横坐标相等是特殊情况,应特殊判断.再证明两条直线平行时,要区分平行与重合,必须强调不共线才能确定平行.因为斜率相等也可以推出两条直线重合.
(2)应用两条直线平行求参数值时,应分斜率存在与不存在两种情况求解.
方法归纳
变式训练
(1)由题意知方程2x2-4x+m-1=0的两实根相等,所以Δ=(-4)2-4×2×(m-1)=0.解之得m=3.
1.(1)已知两平行直线的斜率是方程2x2-4x+m-1=0的两实根,则m的值为( )
A.1 B.-1 C.3 D.-3
(2)已知P(-2,m),Q(m,4),M(m+2,3),N(1,1),若直线PQ∥直线MN,求m的值.
解析
C
(2)当时,直线PQ的斜率不存在,而直线MN的斜率存在,MN与PQ不平行,不合题意;
当时,直线MN的斜率不存在,而直线PQ的斜率存在,MN与PQ不平行,不合题意;
当且时,kPQ== , kMN== .
变式训练
1.(1)已知两平行直线的斜率是方程2x2-4x+m-1=0的两实根,则m的值为( )
A.1 B.-1 C.3 D.-3
(2)已知P(-2,m),Q(m,4),M(m+2,3),N(1,1),若直线PQ∥直线MN,求m的值.
解析
C
因为直线PQ∥直线MN,所以kPQ=kMN,即,解得m=0或m=1.
当m=0或1时,由图形知,两直线不重合.
综上,m的值为0或1.
典例讲解
例3、(1)直线l1经过点A(3,2),B(3,-1),直线l2经过点M(1,1),N(2,1),判断l1与l2是否垂直;
(2)已知直线l1经过点A(3,a),B(a-2,3),直线l2经过点C(2,3),D(-1,a-2),若l1⊥l2,求a的值.
(1)直线l1的斜率不存在,直线l2的斜率为0,所以l1⊥l2.
(2)由题意,知直线l2的斜率k2一定存在,直线l1的斜率可能不存在.
当直线l1的斜率不存在时,3=a-2,即a=5,此时k2=0,则l1⊥l2,满足题意.
当直线的斜率存在时,, .由,知,即×,解得.综上所述, 的值为0或5.
解析
(1)若斜率存在,求出斜率,利用垂直的条件判断;若斜率不存在,可结合图形判断.
(2)当两直线的斜率都存在时,由斜率之积等于-1求解;若一条直线的斜率不存在,由另一条直线的斜率为0求解.
(3)计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式时要对参数进行讨论.
方法归纳
变式训练
2.直线l1,l2的斜率是方程x2-2021x-1=0的两实根,则l1与l2的关系是__________.
Δ=(-2 021)2-4×1×(-1)=2 0212+4>0,x1x2=-1.即l1、l2的斜率之积k1k2=-1. 所以l1⊥l2.
l1⊥l2
解析
例4、如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5 m,宽AB=3 m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?
典例讲解
由AD=5 m,AB=3 m,可得C(5,0),D(5,3),A(0,3).设点M的坐标为(x,0),因为AC⊥DM,所以kAC·kDM=-1.所以× =-1,即x= =3.2,
即当BM=3.2 m时,两条小路AC与DM相互垂直.
解析
如图,以点B为坐标原点,BC,BA所在直线分别为x轴,y轴建立直角坐标系.
(1)建立恰当的直角坐标系;
(2)将“形”转化为“数”进行运算;
(3)将计算结果转化为实际问题中的所求解问题.
利用坐标法解决实际问题的三个步骤
方法归纳
变式训练
3.已知A(2,2+2),B(-2,2),C(0,2-2 ),D(4,2)四个点,顺次连接这四点,试判断四边形ABCD的形状.(说明理由)
因为kAB= = ,kBC= =-,
kAD= =- ,kCD= = ,所以kAB=kCD,kBC=kAD.
所以AB∥CD且BC∥AD,所以四边形是平行四边形,
解析
又因为,所以⊥,所以四边形是矩形.
又因为,,,
所以四边形不是正方形,所以四边形是矩形
(1)当直线l1∥直线l2时,可能它们的斜率都存在且相等,也可能斜率都不存在.
(2)直线l1,l2的斜率分别为k1,k2,当k1=k2时,l1∥l2或l1与l2重合.
(3)对于不重合的直线l1,l2,其倾斜角分别为α,β,有l1∥l2 α=β.
素养提炼
理解两条直线平行与斜率之间的关系
(1)利用l1⊥l2 k1·k2=-1,判断两条直线垂直的前提是这两条直线的斜率都存在,且都不为0.
(2)如果k1·k2≠-1,则这两条直线一定不会垂直.
(3)若两条直线中,一条直线斜率不存在,同时另一条直线斜率等于零,则这两条直线垂直.
这样,两条直线垂直的判定的条件就可叙述为:l1⊥l2 k1·k2=-1或一条直线斜率不存在,同时另一条直线斜率等于零.
素养提炼
理解两条直线垂直与斜率之间的关系
用坐标法研究数学问题是指在平面直角坐标系的基础上,
用坐标表示点,用方程表示曲线,通过对坐标和方程的代数化处理,
来解决平面图形的性质或平面图形中一些位置关系的判定.
素养提炼
坐标法解决数学问题的指导思想
当堂练习
解析
1.已知A(2,0),B(3,3),直线l∥AB,则直线l的斜率k等于( )
A.-3 B.3 C.- D.
B
因为直线l ∥AB,所以
2.若经过点(3,a)、(-2,0)的直线与经过点(3,-4)且斜率为的直线垂直,则a的值为( )
A. B. C.10 D.-10
D
解析
当堂练习
3.若不同两点P、Q的坐标分别为(a,b),(3-b,3-a),则线段PQ的垂直平分线的斜率为________.
由两点的斜率公式可得:,所以线段PQ的垂直平分线的斜率为-1.
-1
解析
4.已知点A(1,2)和点B(0,0),点P在y轴上,若∠BAP为直角,则点P的坐标为________.
设P(0,y),因为∠BAP为直角,所以kAB·kAP=-1,即,解得.
解析
当堂练习
5.已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,试求点D的坐标.
设D(x,y),
∵AB⊥CD且AD∥BC,
.
解析
归纳小结
两直线的位置关系
平行
重合
相交
斜截式方程的判定
一般式方程的判定
垂直
斜截式方程的判定
一般式方程的判定
交点坐标
作 业
课本P91页练习第1,4题
P92页练习第2,6题
