【新课标】6.1.1平均数 课件(共22张PPT)
文档属性
| 名称 | 【新课标】6.1.1平均数 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 10:56:15 | ||
图片预览







文档简介
(共22张PPT)
6.1.1平均数
北师大版八年级上册
教学目标
1.掌握算术平均数和加权平均数的概念,会求一组数据的算术平均数和加权平均数。
2.会用算术平均数和加权平均数解决实际生活中的题。
情境导入
右图表示的是甲、乙、丙三人的射击成绩,谁的成绩更好,谁更稳定?你是怎么判断的?除了直观感觉外,我们如何用量化的数据来刻画“更好”“更稳定”呢?
新知讲解
在篮球比赛中,队员的身高、年龄都是影响球队实力的因素,如何衡量两个球队队员的身高?怎样理解“甲队队员的身高比乙队更高”?怎样理解“甲队队员比乙队更年轻”?
中国男子篮球职业联赛2011~2012赛季冠、亚军球队队员身高、年龄如下:
北京金隅队 广东东莞银行队
号码 身高/cm 年龄/岁 号码 身高/cm 年龄/岁
3 188 35 3 205 31
6 175 28 5 206 21
7 190 27 6 188 23
8 188 22 7 196 29
新知讲解
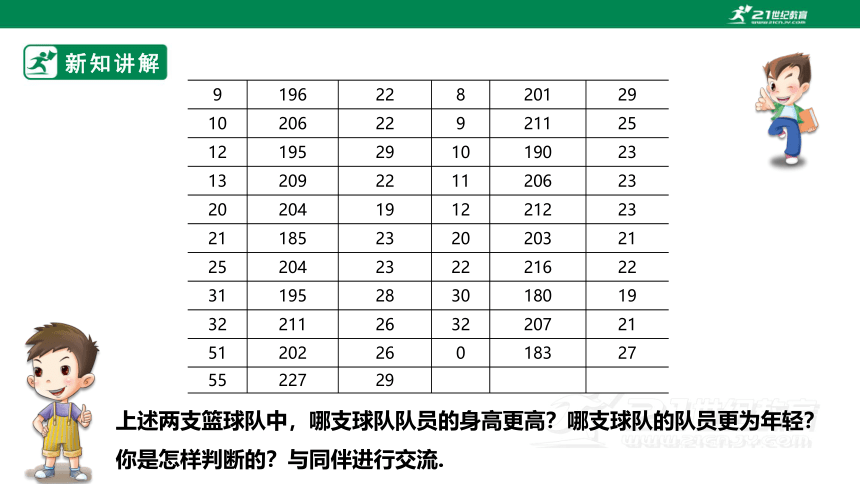
9 196 22 8 201 29
10 206 22 9 211 25
12 195 29 10 190 23
13 209 22 11 206 23
20 204 19 12 212 23
21 185 23 20 203 21
25 204 23 22 216 22
31 195 28 30 180 19
32 211 26 32 207 21
51 202 26 0 183 27
55 227 29
上述两支篮球队中,哪支球队队员的身高更高?哪支球队的队员更为年轻?你是怎样判断的?与同伴进行交流.
归纳总结
算术平均数:一般地,如果有 n 个数 x1,x2, ,xn,那么我们把 (x1+x2+ +xn) 叫做这 n 个数的算术平均数,简称平均数,记作 ,读作 x 拔,则 =(x1+x2+ +xn).
想一想
小明是这样计算北京金隅队队员的平均年龄的:
平均年龄=(19×1+22×4+23×2+26×2+27×1+28×2+29×2+35×1)÷(1+4+2+2+1+2+2+1)=25.4(岁)
你能说说小明这样做的道理吗?
典例精析
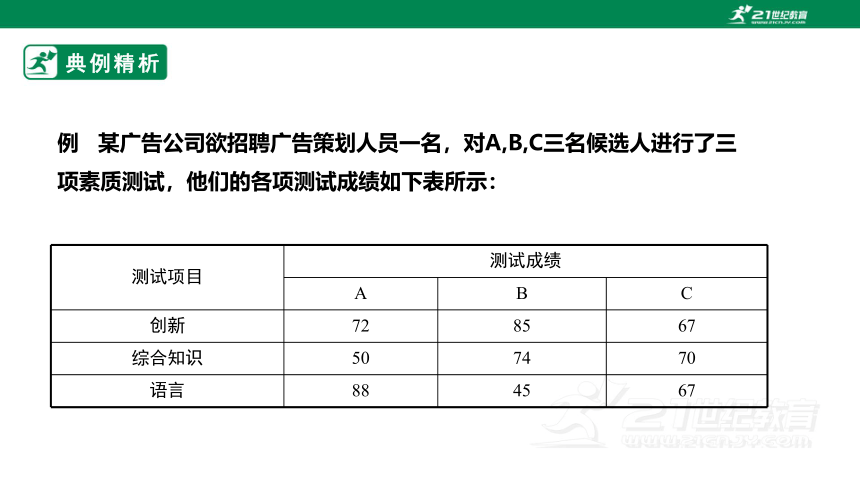
例 某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目 测试成绩
A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
典例精析
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人的测试成绩,此时谁将被录用?
解:(1)A的平均成绩为(72+50+88)/3=70(分).
B的平均成绩为(85+74+45)/3=68(分).
C的平均成绩为(67+70+67)/3=68(分).
由70>68,故A被录用.
典例精析
(2)根据题意,
A的测试成绩为
B的测试成绩为
C的测试成绩为
因此候选人B将被录用.
4,3,1 分别是创新、综合知识、语言三项测试成绩的权,而称(72×4+50×3+88×1)÷(4+3+1)
为A的三项测试成绩的加权平均数.
归纳总结
加权平均数:一般地,若 n 个数 x1,x2, ,xn 的权分别是 w1,w2, ,wn,那么我们把 叫做这 n 个数的加权平均数.
在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.
归纳总结
(1)权能够反映某个数据的重要程度,权越大,该数据所占的比重越大;权越小,该数据所占的比重越小.
(2)权常见的三种表现形式:①数据出现的次数(个数)的形式;②百分数的形式;③连比的形式.
课堂练习
1.小明上学期期末语文、数学、英语三科平均分为92分,她记得语文得了88分,英语得了95分,但她把数学成绩忘记了,你能告诉她应是以下哪个分数吗?( )
A. 93分 B. 95分 C.92.5分 D. 94分
2.某市连续七天的最高温度分别为32,34,35,33,37,38,36(单位:℃).这组数据的平均数是( )
A.36 ℃ B.35 ℃ C.34 ℃ D.33 ℃
A
B
课堂练习
3.为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是________mg/L.
1
课堂练习
4.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是________.
8
5.已知数据x1,x2,x3,…,xn的平均数为m,则数据5x1,5x2,5x3,…,5xn的平均数为 .
5m
课堂练习
6.“五一”期间,新华商场贴出促销海报,内容如图①.在商场活动期间,王莉和同组同学随机调查了部分参加活动的顾客,统计了200人次的摸奖情况,绘制成如图②所示的统计图.
(1)补全统计图;
(2)求所调查的200人次摸奖的获奖率;
(3)若商场每天约有2 000人次摸奖,
请估算商场一天送出的购物券总
金额是多少元.
课堂练习
解:(1)补全统计图,如图所示.
(2)摸奖的获奖率:
×100%=39%.
(3)x==6.675(元).
6.675×2 000=13 350(元).
答:估计商场一天送出的购物券总金额是13 350元.
课堂总结
平均数
算术平均数
加权平均数
板书设计
平均数
1.算术平均数
2.加权平均数
作业布置
教材138页习题第1,3,4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.1.1平均数
北师大版八年级上册
教学目标
1.掌握算术平均数和加权平均数的概念,会求一组数据的算术平均数和加权平均数。
2.会用算术平均数和加权平均数解决实际生活中的题。
情境导入
右图表示的是甲、乙、丙三人的射击成绩,谁的成绩更好,谁更稳定?你是怎么判断的?除了直观感觉外,我们如何用量化的数据来刻画“更好”“更稳定”呢?
新知讲解
在篮球比赛中,队员的身高、年龄都是影响球队实力的因素,如何衡量两个球队队员的身高?怎样理解“甲队队员的身高比乙队更高”?怎样理解“甲队队员比乙队更年轻”?
中国男子篮球职业联赛2011~2012赛季冠、亚军球队队员身高、年龄如下:
北京金隅队 广东东莞银行队
号码 身高/cm 年龄/岁 号码 身高/cm 年龄/岁
3 188 35 3 205 31
6 175 28 5 206 21
7 190 27 6 188 23
8 188 22 7 196 29
新知讲解
9 196 22 8 201 29
10 206 22 9 211 25
12 195 29 10 190 23
13 209 22 11 206 23
20 204 19 12 212 23
21 185 23 20 203 21
25 204 23 22 216 22
31 195 28 30 180 19
32 211 26 32 207 21
51 202 26 0 183 27
55 227 29
上述两支篮球队中,哪支球队队员的身高更高?哪支球队的队员更为年轻?你是怎样判断的?与同伴进行交流.
归纳总结
算术平均数:一般地,如果有 n 个数 x1,x2, ,xn,那么我们把 (x1+x2+ +xn) 叫做这 n 个数的算术平均数,简称平均数,记作 ,读作 x 拔,则 =(x1+x2+ +xn).
想一想
小明是这样计算北京金隅队队员的平均年龄的:
平均年龄=(19×1+22×4+23×2+26×2+27×1+28×2+29×2+35×1)÷(1+4+2+2+1+2+2+1)=25.4(岁)
你能说说小明这样做的道理吗?
典例精析
例 某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目 测试成绩
A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
典例精析
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人的测试成绩,此时谁将被录用?
解:(1)A的平均成绩为(72+50+88)/3=70(分).
B的平均成绩为(85+74+45)/3=68(分).
C的平均成绩为(67+70+67)/3=68(分).
由70>68,故A被录用.
典例精析
(2)根据题意,
A的测试成绩为
B的测试成绩为
C的测试成绩为
因此候选人B将被录用.
4,3,1 分别是创新、综合知识、语言三项测试成绩的权,而称(72×4+50×3+88×1)÷(4+3+1)
为A的三项测试成绩的加权平均数.
归纳总结
加权平均数:一般地,若 n 个数 x1,x2, ,xn 的权分别是 w1,w2, ,wn,那么我们把 叫做这 n 个数的加权平均数.
在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.
归纳总结
(1)权能够反映某个数据的重要程度,权越大,该数据所占的比重越大;权越小,该数据所占的比重越小.
(2)权常见的三种表现形式:①数据出现的次数(个数)的形式;②百分数的形式;③连比的形式.
课堂练习
1.小明上学期期末语文、数学、英语三科平均分为92分,她记得语文得了88分,英语得了95分,但她把数学成绩忘记了,你能告诉她应是以下哪个分数吗?( )
A. 93分 B. 95分 C.92.5分 D. 94分
2.某市连续七天的最高温度分别为32,34,35,33,37,38,36(单位:℃).这组数据的平均数是( )
A.36 ℃ B.35 ℃ C.34 ℃ D.33 ℃
A
B
课堂练习
3.为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是________mg/L.
1
课堂练习
4.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是________.
8
5.已知数据x1,x2,x3,…,xn的平均数为m,则数据5x1,5x2,5x3,…,5xn的平均数为 .
5m
课堂练习
6.“五一”期间,新华商场贴出促销海报,内容如图①.在商场活动期间,王莉和同组同学随机调查了部分参加活动的顾客,统计了200人次的摸奖情况,绘制成如图②所示的统计图.
(1)补全统计图;
(2)求所调查的200人次摸奖的获奖率;
(3)若商场每天约有2 000人次摸奖,
请估算商场一天送出的购物券总
金额是多少元.
课堂练习
解:(1)补全统计图,如图所示.
(2)摸奖的获奖率:
×100%=39%.
(3)x==6.675(元).
6.675×2 000=13 350(元).
答:估计商场一天送出的购物券总金额是13 350元.
课堂总结
平均数
算术平均数
加权平均数
板书设计
平均数
1.算术平均数
2.加权平均数
作业布置
教材138页习题第1,3,4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
