4.2 第1课时直线、射线、线段的概念与性质 课件(共22张PPT)
文档属性
| 名称 | 4.2 第1课时直线、射线、线段的概念与性质 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-07 14:59:55 | ||
图片预览






文档简介
(共22张PPT)
4.2 第1课时直线、射线、线段的概念与性质
人教版 七年级上册
教学目标
教学目标:
1.能在现实情境中,经历画图的数学活动过程,理解并掌握直线的性质,能用几何语言描述直线性质;会用字母表示直线、射线、线段,会根据语言描述画出图形。
2.能在现实情境中,进行抽象的数学思考,提高抽象概括能力,经历画图的数学活动过程,提高学生的动手操作与实践能力。
3.体验通过实验获得数学猜想,得到直线性质的过程。
重点:理解并掌握直线性质,会用字母表示图形和根据语言描述画出图形。
难点:根据语言描述画出图形.
情景导入
我们在小学已经学过线段、射线和直线,观察欣赏这一组生活中的图片,从中你能找出我们熟悉的线段、射线和直线吗?它们有什么联系和区别吗?
电筒射出的光线
笔直的公路
射线
直线
线段
绷紧的琴弦
区别:直线没有端点,射线有一个端点,线段有两个端点.
联系:都是直直的线.
合作探究
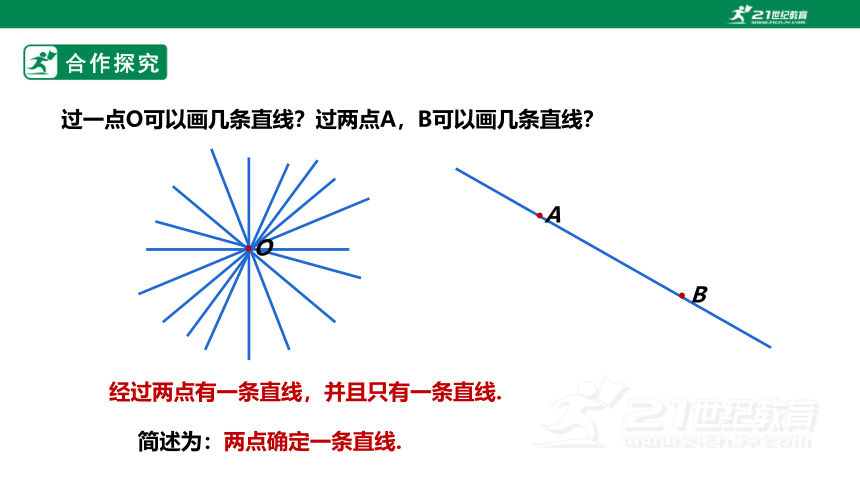
过一点O可以画几条直线?过两点A,B可以画几条直线?
经过两点有一条直线,并且只有一条直线.
简述为:两点确定一条直线.
·O
·A
·B
合作探究
两点确定一条直线可以用来说明生活中的现象.
1. 建筑工人砌墙时,会在两个墙角的位置分别插 一根木桩,然后拉一条直的参考线.
合作探究
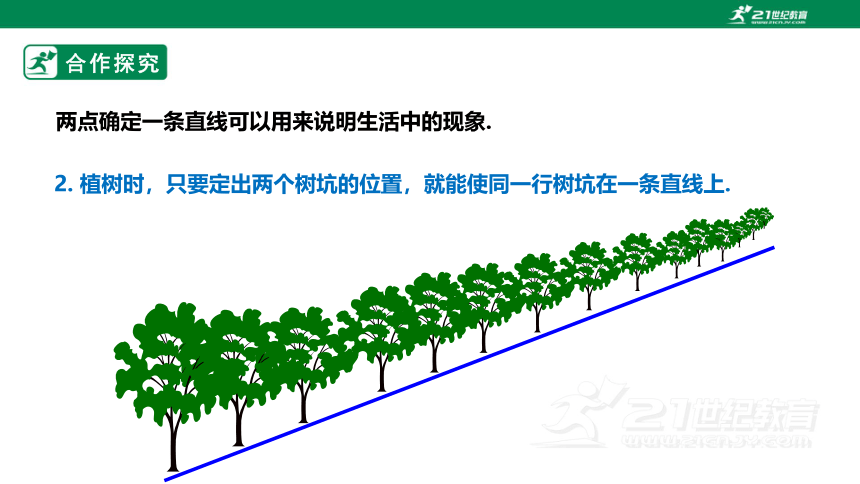
2. 植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上.
两点确定一条直线可以用来说明生活中的现象.
合作探究
一般地,几何图形都有对应的符号语言表示,直线如何表示呢?
1.用一个小写的英文字母表示,如:直线l.
2.用直线上的两个点来表示,如:直线AB(或直线BA).
l
A B
同时,也可以说点A、B在直线l上
l
合作探究
观察下图,说一说点和直线有哪些位置关系.
A
B
l
如图:点 A 在直线 l 上,点 B 在直线 l 外
或者说:直线 l 经过点 A,
点 B 不在直线 l 上 (直线 l 不经过点B ).
合作探究
b
a
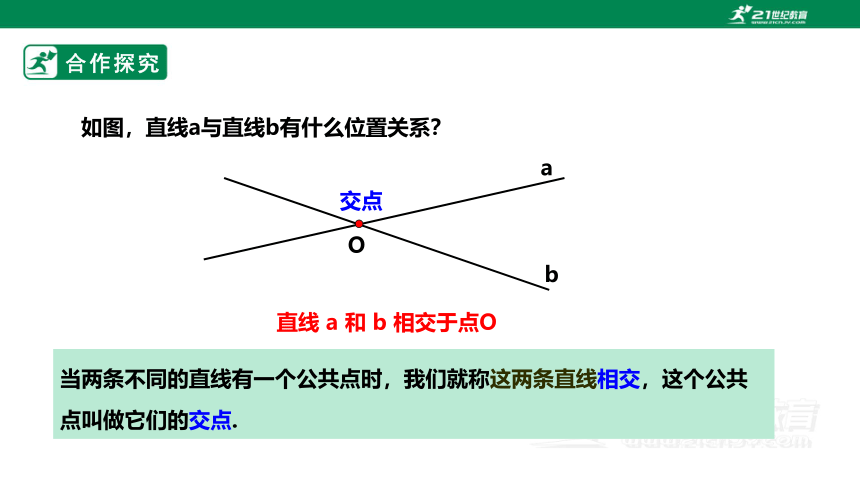
如图,直线a与直线b有什么位置关系?
交点
O
直线 a 和 b 相交于点O
当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点.
合作探究
线段a 线段AB 线段BA
a
A
B
射线l 射线OA(端点字母在前)
注意:用两个大写字母表示射线或线段.
(1)表示射线时,前一个字母表示射线的端点,后一个字母表示射线上除端点外的任意一点.
(2)表示线段时,两个字母的顺序无特殊要求.
线段和射线都是直线的一部分,类比直线的表示方法,线段和射线又如何表示呢?
图形
表示方法
合作探究
A
B
A
B
直线、射线、线段三者的联系:
A
B
2. 将线段向两个方向无限延长就形成了直线.
1. 将线段向一个方向无限延长就形成了射线.
分别画一条直线、射线和线段,议一议它们之间的联系和区别.
线段和射线都是直线的一部分.
合作探究
线段、射线、直线的区别与联系
类型 端点数 可否延伸 可否度量
线段
射线
直线
2个
不能延伸
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
归纳总结
基本事实:
经过两点有一条直线,并且只有一条直线.
简单记为:两点确定一条直线.
直线、射线、线段的表示方法:
(1)用一个小写英文字母表示;
(2)用线上的两个点表示.
直线l或直线 AB(BA)
射线l或射线OA
线段 a或线段 AB(BA)
点与直线的位置关系:
(1)点在直线上(直线经过点);
(2)点在直线外(直线不经过点).
课堂练习
1.判断下列说法是否正确,并说明理由.
(1)线段AB和射线AB都是直线AB的一部分. ( )
(2)直线AB和直线BA是同一条直线. ( )
(3)射线AB和射线BA是同一条射线. ( )
(4)把线段向一个方向无限延伸可得到射线,向两个方向无限延伸可得到直线. ( )
√
√
√
×
课堂练习
3. 下列表示方法正确的是( )
A. 线段L B. 直线ab
C. 直线m D. 射线Oa
C
2. 在同一平面内有三个点A,B,C,过其中任意两个点做直线,可以画出的直线的条数是( )
A. 1 B. 2 C. 1或3 D. 无法确定
C
课堂练习
4.如图,表示方法正确的是( )
解:不能用一个大写字母表示直线,故①错误;
可以用一个小写字母表示射线,故②正确;
③中的射线应表示为射线OA,故③错误;
可用表示线段两个端点的大写字母表示线段,故④正确.
综上,表示方法正确的只有②④.
A.①② B.②④ C.③④ D.①④
B
课堂练习
5.平面上不同的两点确定1条直线,不同的三点最多可确定3条直线,若平面上不同的八个点最多可确定 n 条直线,则 n 的值是( )
A.26 B.27 C.28 D.29
解:平面上不同的两点确定1条直线;
不同的三点最多可确定1+2=3条直线;
不同的四点最多可确定1+2+3=6条直线;
不同的五点最多可确定1+2+3+4 =10条直线……
所以平面上不同的八点最多可确定1+2+3+4+5+6+7=28条直线.
C
课堂练习
6.如图,射线PA与PB是同一条射线,则符合题意的图为( )
P
A
B
P
P
P
P
A
A
A
B
B
B
A
B
C
D
C
课堂练习
7. 如图,A,B,C三点在一条直线上,
(1) 图中有几条直线,怎样表示它们?
(2) 图中有几条线段,怎样表示它们?
(3) 射线 AB 和射线 AC 是同一条射线吗?
(4) 图中有几条射线?写出以点B为端点的射线.
A
B
C
解:(1) 1条,直线AB或直线AC或直线BC;
(2) 3条,线段AB,线段BC,线段AC;
(3) 是;(4) 6条.以B为端点的射线有射线BC、射线BA.
直线、射线、线段的表示方法:
基本事实:
经过两点有一条直线,并且只有一条直线.
简单记为:两点确定一条直线.
(1)用一个小写英文字母表示;
(2)用两个大写字母表示.
直线
射线
线段
直线l或直线 AB(BA)
射线l或射线OA
线段 a或线段 AB(BA)
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.2 第1课时直线、射线、线段的概念与性质
人教版 七年级上册
教学目标
教学目标:
1.能在现实情境中,经历画图的数学活动过程,理解并掌握直线的性质,能用几何语言描述直线性质;会用字母表示直线、射线、线段,会根据语言描述画出图形。
2.能在现实情境中,进行抽象的数学思考,提高抽象概括能力,经历画图的数学活动过程,提高学生的动手操作与实践能力。
3.体验通过实验获得数学猜想,得到直线性质的过程。
重点:理解并掌握直线性质,会用字母表示图形和根据语言描述画出图形。
难点:根据语言描述画出图形.
情景导入
我们在小学已经学过线段、射线和直线,观察欣赏这一组生活中的图片,从中你能找出我们熟悉的线段、射线和直线吗?它们有什么联系和区别吗?
电筒射出的光线
笔直的公路
射线
直线
线段
绷紧的琴弦
区别:直线没有端点,射线有一个端点,线段有两个端点.
联系:都是直直的线.
合作探究
过一点O可以画几条直线?过两点A,B可以画几条直线?
经过两点有一条直线,并且只有一条直线.
简述为:两点确定一条直线.
·O
·A
·B
合作探究
两点确定一条直线可以用来说明生活中的现象.
1. 建筑工人砌墙时,会在两个墙角的位置分别插 一根木桩,然后拉一条直的参考线.
合作探究
2. 植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上.
两点确定一条直线可以用来说明生活中的现象.
合作探究
一般地,几何图形都有对应的符号语言表示,直线如何表示呢?
1.用一个小写的英文字母表示,如:直线l.
2.用直线上的两个点来表示,如:直线AB(或直线BA).
l
A B
同时,也可以说点A、B在直线l上
l
合作探究
观察下图,说一说点和直线有哪些位置关系.
A
B
l
如图:点 A 在直线 l 上,点 B 在直线 l 外
或者说:直线 l 经过点 A,
点 B 不在直线 l 上 (直线 l 不经过点B ).
合作探究
b
a
如图,直线a与直线b有什么位置关系?
交点
O
直线 a 和 b 相交于点O
当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点.
合作探究
线段a 线段AB 线段BA
a
A
B
射线l 射线OA(端点字母在前)
注意:用两个大写字母表示射线或线段.
(1)表示射线时,前一个字母表示射线的端点,后一个字母表示射线上除端点外的任意一点.
(2)表示线段时,两个字母的顺序无特殊要求.
线段和射线都是直线的一部分,类比直线的表示方法,线段和射线又如何表示呢?
图形
表示方法
合作探究
A
B
A
B
直线、射线、线段三者的联系:
A
B
2. 将线段向两个方向无限延长就形成了直线.
1. 将线段向一个方向无限延长就形成了射线.
分别画一条直线、射线和线段,议一议它们之间的联系和区别.
线段和射线都是直线的一部分.
合作探究
线段、射线、直线的区别与联系
类型 端点数 可否延伸 可否度量
线段
射线
直线
2个
不能延伸
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
归纳总结
基本事实:
经过两点有一条直线,并且只有一条直线.
简单记为:两点确定一条直线.
直线、射线、线段的表示方法:
(1)用一个小写英文字母表示;
(2)用线上的两个点表示.
直线l或直线 AB(BA)
射线l或射线OA
线段 a或线段 AB(BA)
点与直线的位置关系:
(1)点在直线上(直线经过点);
(2)点在直线外(直线不经过点).
课堂练习
1.判断下列说法是否正确,并说明理由.
(1)线段AB和射线AB都是直线AB的一部分. ( )
(2)直线AB和直线BA是同一条直线. ( )
(3)射线AB和射线BA是同一条射线. ( )
(4)把线段向一个方向无限延伸可得到射线,向两个方向无限延伸可得到直线. ( )
√
√
√
×
课堂练习
3. 下列表示方法正确的是( )
A. 线段L B. 直线ab
C. 直线m D. 射线Oa
C
2. 在同一平面内有三个点A,B,C,过其中任意两个点做直线,可以画出的直线的条数是( )
A. 1 B. 2 C. 1或3 D. 无法确定
C
课堂练习
4.如图,表示方法正确的是( )
解:不能用一个大写字母表示直线,故①错误;
可以用一个小写字母表示射线,故②正确;
③中的射线应表示为射线OA,故③错误;
可用表示线段两个端点的大写字母表示线段,故④正确.
综上,表示方法正确的只有②④.
A.①② B.②④ C.③④ D.①④
B
课堂练习
5.平面上不同的两点确定1条直线,不同的三点最多可确定3条直线,若平面上不同的八个点最多可确定 n 条直线,则 n 的值是( )
A.26 B.27 C.28 D.29
解:平面上不同的两点确定1条直线;
不同的三点最多可确定1+2=3条直线;
不同的四点最多可确定1+2+3=6条直线;
不同的五点最多可确定1+2+3+4 =10条直线……
所以平面上不同的八点最多可确定1+2+3+4+5+6+7=28条直线.
C
课堂练习
6.如图,射线PA与PB是同一条射线,则符合题意的图为( )
P
A
B
P
P
P
P
A
A
A
B
B
B
A
B
C
D
C
课堂练习
7. 如图,A,B,C三点在一条直线上,
(1) 图中有几条直线,怎样表示它们?
(2) 图中有几条线段,怎样表示它们?
(3) 射线 AB 和射线 AC 是同一条射线吗?
(4) 图中有几条射线?写出以点B为端点的射线.
A
B
C
解:(1) 1条,直线AB或直线AC或直线BC;
(2) 3条,线段AB,线段BC,线段AC;
(3) 是;(4) 6条.以B为端点的射线有射线BC、射线BA.
直线、射线、线段的表示方法:
基本事实:
经过两点有一条直线,并且只有一条直线.
简单记为:两点确定一条直线.
(1)用一个小写英文字母表示;
(2)用两个大写字母表示.
直线
射线
线段
直线l或直线 AB(BA)
射线l或射线OA
线段 a或线段 AB(BA)
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
