4.3.2 角的比较与运算 课件(共26张PPT)
文档属性
| 名称 | 4.3.2 角的比较与运算 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-07 15:01:40 | ||
图片预览





文档简介
(共26张PPT)
4.3.2角的比较与运算
人教版 七年级上册
教学目标
教学目标:
1.会比较较的大小,理解角平分线的定义.
2.能根据图形进行角的和、差、倍、分的计算,会利用三角尺画特殊角度的角.
3.能通过角的比较等体验数、符号和图形是描述现实世界的重要手段.
重点:角的大小的比较方法.
难点:角平分线和角的和与差.
新知导入
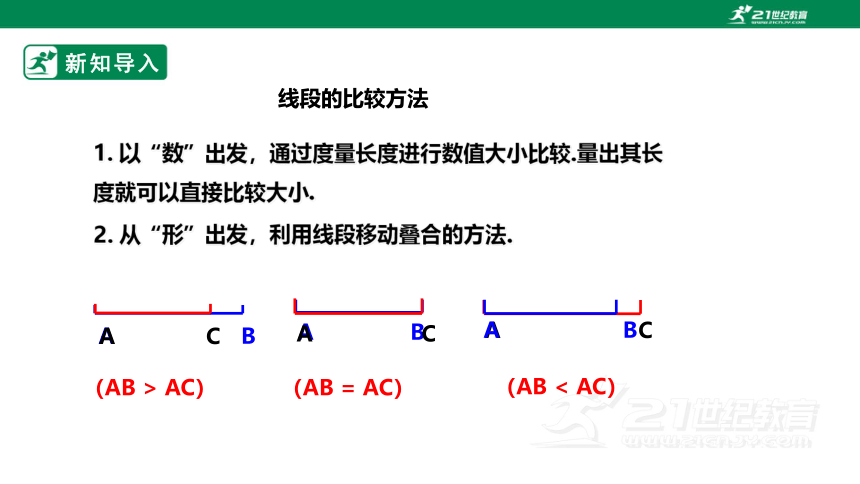
线段的比较方法
2. 从“形”出发,利用线段移动叠合的方法.
1. 以“数”出发,通过度量长度进行数值大小比较.量出其长度就可以直接比较大小.
A
C
A
B
C
A
A
B
A
B
(AB > AC)
(AB = AC)
(AB < AC)
A
C
新知讲解
我们已经知道了怎样比较两条线段的长短,类似的,怎样比较两个角的大小呢?
与线段大小比较类似,我们可以用量角器量出角的度数,然后比较它们的大小;也可以把它们叠合在一起比较大小.
新知讲解
一.度量法
1.对“中”—角的顶点对量角器的中心
2.重合—角的一边与量角器的0°刻度线重合
3.读数—读出角的另一边所对的度数
F
E
D
30°
∠ABC > ∠DEF
新知讲解
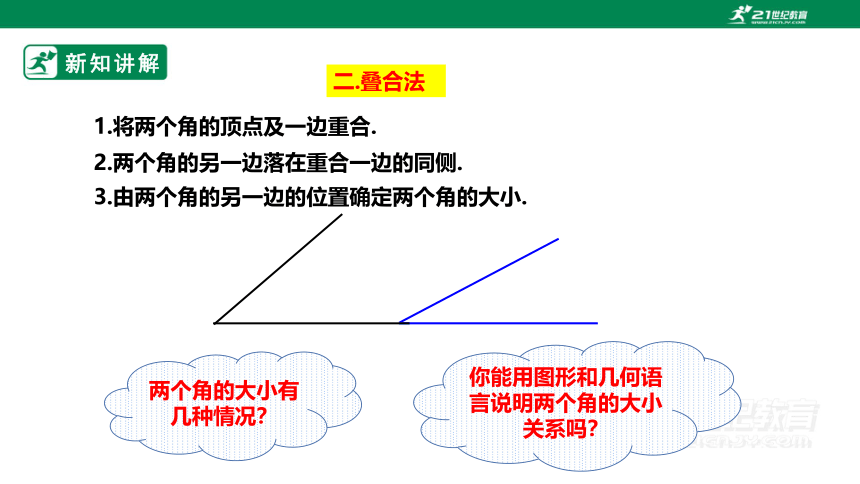
二.叠合法
1.将两个角的顶点及一边重合.
2.两个角的另一边落在重合一边的同侧.
3.由两个角的另一边的位置确定两个角的大小.
两个角的大小有几种情况?
你能用图形和几何语言说明两个角的大小关系吗?
新知讲解
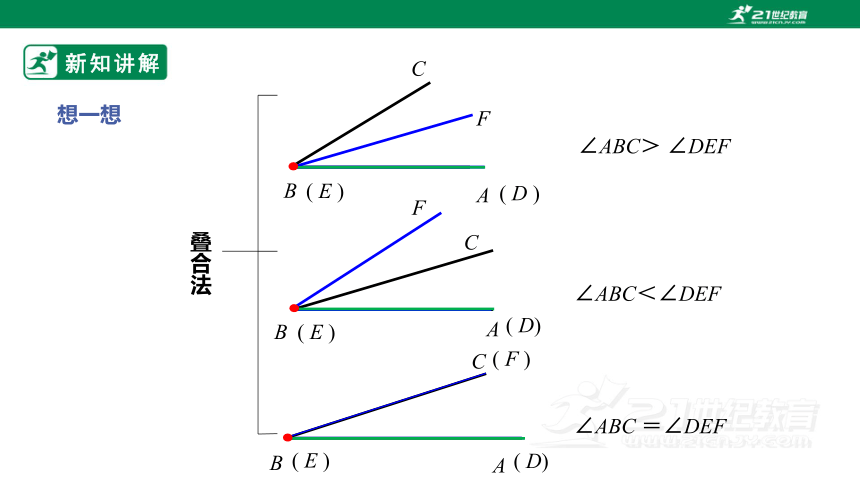
想一想
A
B
C
F
( E )
( D)
A
B
C
( E )
( D)
( F )
A
B
C
F
( E )
( D )
叠合法
∠ABC> ∠DEF
∠ABC<∠DEF
∠ABC =∠DEF
新知讲解
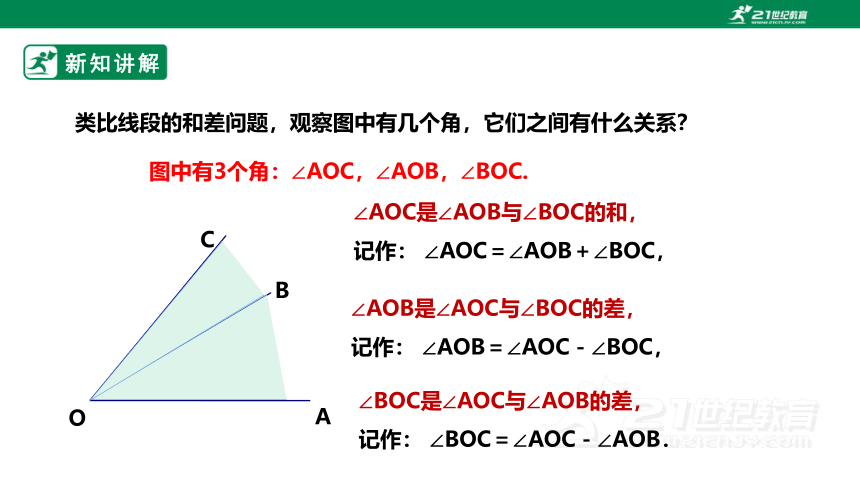
类比线段的和差问题,观察图中有几个角,它们之间有什么关系?
∠BOC是∠AOC与∠AOB的差,
记作: ∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与∠BOC的和,
记作: ∠AOC=∠AOB+∠BOC,
∠AOB是∠AOC与∠BOC的差,
记作: ∠AOB=∠AOC-∠BOC,
O
C
B
A
图中有3个角:∠AOC,∠AOB,∠BOC.
新知讲解
利用一副三角板,你能画出哪些度数的角?试一试.
15°
75°
你还能画出其他角度吗?
新知讲解
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.
类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
新知讲解
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
O
B
A
C
注意:
角平分线是在角的内部从角的顶点引出的一条射线,不是直线或线段;
新知讲解
角的n等分线:类似角的平分线,从角的顶点引出的射线,将角分成相等的n个角,叫做角的n等分线,
将一个角三等分
射线OC、OD为∠AOB的三等分线
将一个角四等分
射线OC、OD 、OE 为∠AOB的四等分线
新知讲解
线段的中点
角平分线
文字语言
图形语言
符号语言
点C 把线段AB 分成相等的两条线段AC 和CB,点C 叫做线段AB 的中点
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线
A
B
C
C
A
B
O
(1)∵C 为线段AB 中点
∴AC =BC =AB
(1)∵ OC 平分∠AOB,
∴∠1=∠2= ∠AOB
(2)∵C 为线段AB 中点
∴AB =2AC =2BC.
(2)∵ OC 平分∠AOB
∴∠AOB=2∠1=2∠2.
2
1
新知讲解
例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,
求∠BOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
新知讲解
例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
新知讲解
角的大小比较:
1.度量法:量角器.
2.叠合法:将两角的一边重合,由另一边的位置比较大小.
角平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线.
角的和与差:
1.两角之和,记作: ∠AOC=∠AOB+∠BOC.
2.两角之差,记作: ∠AOB=∠AOC-∠BOC.
课堂练习
1.如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于( )
A.20° B.50° C.75° D.100°
2.如图,∠AOB=60°,且∠AOC=∠AOB,则∠BOC= .
D
第1题图
40°
第2题图
课堂练习
∵AD是∠BAC的平分线
∴∠ =∠ .
∵∠ABC=2∠ABE
∴ 平分∠ .
( 角平分线的意义 )
BAD
CAD
BE
ABC
( 角平分线的意义 )
A
B
C
D
E
3. 填空:
课堂练习
4. 如图,∠AOB=∠COD=90,∠AOD=146°,则∠BOC=______.
5. 已知∠AOB=38°,∠BOC=25°,那么∠AOC 的度数是 .
34°
13°或63°
O
A
B
C
D
课堂练习
6.计算:
(1)98°45′36″+71°22′34″= ;
(2)52°37′-31°45′12″= ;
(3)13°24′15″×5= ;
(4)58°34′16″÷4= .
170°8′10″
20°51′48″
67°1′15″
14°38′34″
课堂练习
7. 如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
解:∵∠AOB=120°,
OD平分∠BOC,
OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC
= (∠BOC+∠AOC )
= ∠AOB= ×120°=60°.
课堂练习
(2) 若∠BOC=90°,求∠AOE的度数.
解:∵∠AOB=120°,
∠BOC=90°,
∴∠AOC=120°-90°
=30°.
∵OE平分∠AOC,
∴∠AOE= ∠AOC= ×30°=15°.
课堂练习
8.如图,已知O是直线CD上的点,OA平分∠BOC,∠AOC=35°,求∠BOD的度数.
解:∵O是直线CD上的点,OA平分
∠BOC,∠AOC=35°,
∴∠BOC=2∠AOC=70°,
∴∠BOD=180°-∠BOC
=180°-70°=110°.
课堂小结
角的和与差:
角的大小比较:
1.度量法:量角器.
2.叠合法:将两角的一边重合,由另一边的位置比较大小.
角的比较与运算
角平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线
叫做这个角的角平分线.
1.两角之和,记作: ∠AOC=∠AOB+∠BOC.
2.两角之差,记作: ∠AOB=∠AOC-∠BOC.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.3.2角的比较与运算
人教版 七年级上册
教学目标
教学目标:
1.会比较较的大小,理解角平分线的定义.
2.能根据图形进行角的和、差、倍、分的计算,会利用三角尺画特殊角度的角.
3.能通过角的比较等体验数、符号和图形是描述现实世界的重要手段.
重点:角的大小的比较方法.
难点:角平分线和角的和与差.
新知导入
线段的比较方法
2. 从“形”出发,利用线段移动叠合的方法.
1. 以“数”出发,通过度量长度进行数值大小比较.量出其长度就可以直接比较大小.
A
C
A
B
C
A
A
B
A
B
(AB > AC)
(AB = AC)
(AB < AC)
A
C
新知讲解
我们已经知道了怎样比较两条线段的长短,类似的,怎样比较两个角的大小呢?
与线段大小比较类似,我们可以用量角器量出角的度数,然后比较它们的大小;也可以把它们叠合在一起比较大小.
新知讲解
一.度量法
1.对“中”—角的顶点对量角器的中心
2.重合—角的一边与量角器的0°刻度线重合
3.读数—读出角的另一边所对的度数
F
E
D
30°
∠ABC > ∠DEF
新知讲解
二.叠合法
1.将两个角的顶点及一边重合.
2.两个角的另一边落在重合一边的同侧.
3.由两个角的另一边的位置确定两个角的大小.
两个角的大小有几种情况?
你能用图形和几何语言说明两个角的大小关系吗?
新知讲解
想一想
A
B
C
F
( E )
( D)
A
B
C
( E )
( D)
( F )
A
B
C
F
( E )
( D )
叠合法
∠ABC> ∠DEF
∠ABC<∠DEF
∠ABC =∠DEF
新知讲解
类比线段的和差问题,观察图中有几个角,它们之间有什么关系?
∠BOC是∠AOC与∠AOB的差,
记作: ∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与∠BOC的和,
记作: ∠AOC=∠AOB+∠BOC,
∠AOB是∠AOC与∠BOC的差,
记作: ∠AOB=∠AOC-∠BOC,
O
C
B
A
图中有3个角:∠AOC,∠AOB,∠BOC.
新知讲解
利用一副三角板,你能画出哪些度数的角?试一试.
15°
75°
你还能画出其他角度吗?
新知讲解
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.
类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
新知讲解
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
O
B
A
C
注意:
角平分线是在角的内部从角的顶点引出的一条射线,不是直线或线段;
新知讲解
角的n等分线:类似角的平分线,从角的顶点引出的射线,将角分成相等的n个角,叫做角的n等分线,
将一个角三等分
射线OC、OD为∠AOB的三等分线
将一个角四等分
射线OC、OD 、OE 为∠AOB的四等分线
新知讲解
线段的中点
角平分线
文字语言
图形语言
符号语言
点C 把线段AB 分成相等的两条线段AC 和CB,点C 叫做线段AB 的中点
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线
A
B
C
C
A
B
O
(1)∵C 为线段AB 中点
∴AC =BC =AB
(1)∵ OC 平分∠AOB,
∴∠1=∠2= ∠AOB
(2)∵C 为线段AB 中点
∴AB =2AC =2BC.
(2)∵ OC 平分∠AOB
∴∠AOB=2∠1=2∠2.
2
1
新知讲解
例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,
求∠BOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
新知讲解
例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
新知讲解
角的大小比较:
1.度量法:量角器.
2.叠合法:将两角的一边重合,由另一边的位置比较大小.
角平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线.
角的和与差:
1.两角之和,记作: ∠AOC=∠AOB+∠BOC.
2.两角之差,记作: ∠AOB=∠AOC-∠BOC.
课堂练习
1.如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于( )
A.20° B.50° C.75° D.100°
2.如图,∠AOB=60°,且∠AOC=∠AOB,则∠BOC= .
D
第1题图
40°
第2题图
课堂练习
∵AD是∠BAC的平分线
∴∠ =∠ .
∵∠ABC=2∠ABE
∴ 平分∠ .
( 角平分线的意义 )
BAD
CAD
BE
ABC
( 角平分线的意义 )
A
B
C
D
E
3. 填空:
课堂练习
4. 如图,∠AOB=∠COD=90,∠AOD=146°,则∠BOC=______.
5. 已知∠AOB=38°,∠BOC=25°,那么∠AOC 的度数是 .
34°
13°或63°
O
A
B
C
D
课堂练习
6.计算:
(1)98°45′36″+71°22′34″= ;
(2)52°37′-31°45′12″= ;
(3)13°24′15″×5= ;
(4)58°34′16″÷4= .
170°8′10″
20°51′48″
67°1′15″
14°38′34″
课堂练习
7. 如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
解:∵∠AOB=120°,
OD平分∠BOC,
OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC
= (∠BOC+∠AOC )
= ∠AOB= ×120°=60°.
课堂练习
(2) 若∠BOC=90°,求∠AOE的度数.
解:∵∠AOB=120°,
∠BOC=90°,
∴∠AOC=120°-90°
=30°.
∵OE平分∠AOC,
∴∠AOE= ∠AOC= ×30°=15°.
课堂练习
8.如图,已知O是直线CD上的点,OA平分∠BOC,∠AOC=35°,求∠BOD的度数.
解:∵O是直线CD上的点,OA平分
∠BOC,∠AOC=35°,
∴∠BOC=2∠AOC=70°,
∴∠BOD=180°-∠BOC
=180°-70°=110°.
课堂小结
角的和与差:
角的大小比较:
1.度量法:量角器.
2.叠合法:将两角的一边重合,由另一边的位置比较大小.
角的比较与运算
角平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线
叫做这个角的角平分线.
1.两角之和,记作: ∠AOC=∠AOB+∠BOC.
2.两角之差,记作: ∠AOB=∠AOC-∠BOC.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
