人教B版高中数学必修第一册《2.2.2不等式的解集》(共30张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册《2.2.2不等式的解集》(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 886.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 22:03:07 | ||
图片预览









文档简介
(共30张PPT)
2.2 不等式
第二章 等式与不等式
2.2.2 不等式的解集
学习目标
1.梳理不等式的解集.
2.会解一元一次不等式组.
3.会解简单的绝对值不等式.
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
不等式的解集 数学抽象 水平1 水平2 不等式的解集是继不等式性质后的一个重要章节,求解不等式的解集必须熟练掌握不等式基本性质,同时注意在解不等式时必须是进行同解变形。要掌握不等式、不等式组解集的求法以及绝对不值等式的解集的求法。 【考查内容】在高考中,不等式的解集是必考内容,特别是不等式解法,绝对值不等式的解法,常与其他知识结合起来考查,因此其解集的求法是常考的题型。
【考查题型】填空题、选择题,绝对值不等式的解法常见于解答题中
【分值情况】5~15分
不等式组的解集 数学推理 水平1 水平2 绝对值不等式 数学抽象 水平1 水平2 绝对值不等式的解法 数学运算 水平1 水平2 知识点一 不等式的解集与不等式组的解集
(一)教材梳理填空
一、自学教材·注重基础
(1)不等式的解集
一般地,不等式的________组成的集合称为不等式的解集.
(2)不等式组的解集
对于由若干个不等式联立得到的不等式组来说,这些不等式的解集的________称为不等式组的解集.
(二)基本知能小试
一、自学教材·注重基础
1.判断正误
(1)不等式-2x+1>0的解集为. ( )
(2)ax+b>0的解集为. ( )
×
知识点一 不等式的解集与不等式组的解集
×
2.不等式3x-5<0的解集为________.
解析:由3x-5<0,得3x<5,即x<.
(二)基本知能小试
一、自学教材·注重基础
知识点一 不等式的解集与不等式组的解集
3.不等式组的解集为________.
解析:由2x-1>0,得x>;由x+1<3,得x<2.
∴不等式组的解集为.
知识点二 绝对值不等式
(一)教材梳理填空
一、自学教材·注重基础
(1)绝对值不等式
一般地,含有_________的不等式称为绝对值不等式.
(2)数轴上两点间的距离公式及中点坐标公式
一般地,如果实数a,b在数轴上对应的点分别为A,B,即A(a),B(b),则线段AB的长为|AB|= _________ ,线段AB的中点M对应的数x= _________.
(二)基本知能小试
一、自学教材·注重基础
×
√
×
知识点二 绝对值不等式
1.判断正误
(1)不等式|x|<2的解集为(-2,2). ( )
(2)不等式|x|(3)若a>b,则|a|>|b|. ( )
(4)若|a|>|b|,则a>b. ( )
×
(二)基本知能小试
一、自学教材·注重基础
知识点二 绝对值不等式
2.不等式|2x-1|<5的解集为___________.
解析:由|2x-1|<5,得-5<2x-1<5,即-4<2x<6,∴-2(-2,3)
3.不等式|x-2|>3的解集为_________________.
解析:∵|x-2|>3,
∴x-2>3或x-2<-3,
即x>5或x<-1.
(-∞,-1)∪(5,+∞)
(二)基本知能小试
一、自学教材·注重基础
6
知识点二 绝对值不等式
1
4.数轴上两点A(4),B(-2),则|AB|=________,AB的中点M的坐标为________.
解析:|AB|=|4-(-2)|=6,=1.
题型一 不等式的解法
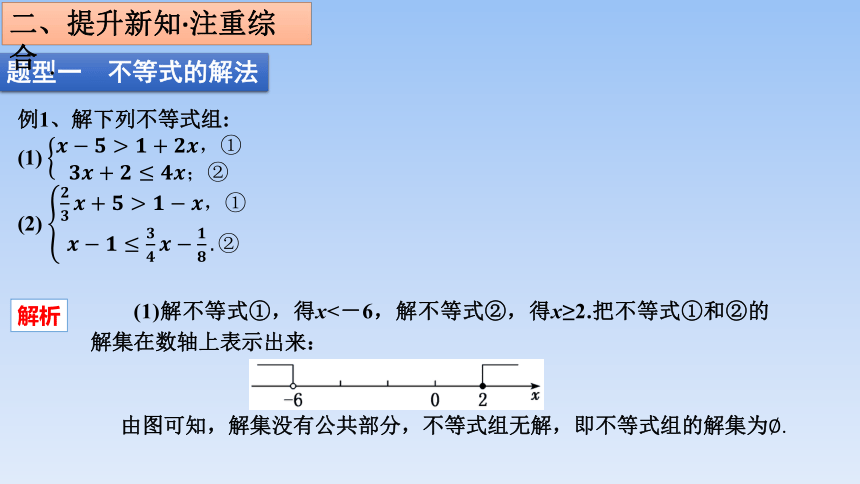
例1、解下列不等式组:
(1)
(2)
解析
二、提升新知·注重综合
(1)解不等式①,得x<-6,解不等式②,得x≥2.把不等式①和②的解集在数轴上表示出来:
由图可知,解集没有公共部分,不等式组无解,即不等式组的解集为.
.
题型一 不等式的解法
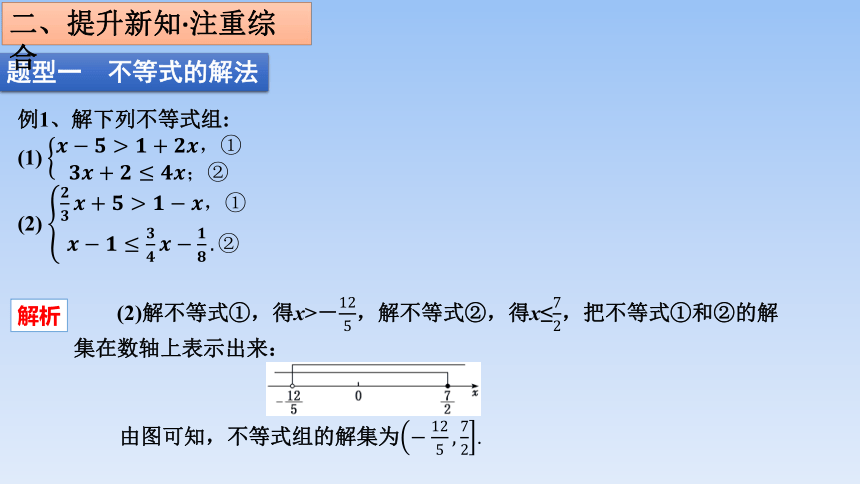
例1、解下列不等式组:
(1)
(2)
解析
二、提升新知·注重综合
(2)解不等式①,得x>-,解不等式②,得x≤,把不等式①和②的解集在数轴上表示出来:
由图可知,不等式组的解集为.
方法总结
二、提升新知·注重综合
(1)求出不等式组中每个不等式的解集;
(2)借助数轴找出各解集的公共部分;
(3)写出不等式组的解集.
解不等式组的三个步骤
题型一 不等式的解法
变式训练
二、提升新知·注重综合
题型一 不等式的解法
1.解不等式组:-1<≤5.
解析:法一:原不等式组可化为下面的不等式组
解不等式①,得x>-1.
解不等式②,得x≤8.
所以不等式组的解集为(-1,8].
法二:由-1<≤5,
可得-3<2x-1≤15,
即-2<2x≤16,
解得-1∴不等式组的解集为(-1,8].
变式训练
二、提升新知·注重综合
题型一 不等式的解法
2.已知关于x的不等式组的解集为(1,3),求a的值.
解析:由2x+1>3,得x>1,
由a-x>1,得x又∵不等式组的解集为(1,3),
∴a-1=3,即a=4.
二、提升新知·注重综合
题型二 含有一个绝对值号不等式的解法
解析
(1)原不等式等价于-7<2x+5<7,
所以-12<2x<2,
所以-6(2)由不等式|2x+5|>7+x,
可得2x+5>7+x或2x+5<-(7+x),
所以x>2或x<-4,
所以原不等式的解集为(-∞,-4)∪(2,+∞).
例2、解下列不等式:
(1)|2x+5|<7;
(2)|2x+5|>7+x;
(3)2≤|x-2|≤4.
二、提升新知·注重综合
题型二 含有一个绝对值号不等式的解法
解析
(3)原不等式等价于
由①得x-2≤-2或x-2≥2,
所以x≤0或x≥4.
例2、解下列不等式:
(1)|2x+5|<7;
(2)|2x+5|>7+x;
(3)2≤|x-2|≤4.
二、提升新知·注重综合
方法总结
(1)求形如|f(x)|0)和|f(x)|>a(a>0)型不等式可运用等价转化法化成等价的不等式(组)求解.
(2)求形如|f(x)|g(x)型不等式的解法
①等价转化法:
|f(x)||f(x)|>g(x) f(x)<-g(x)或f(x)>g(x).
(这里g(x)可正也可负)
②分类讨论法:
|f(x)||f(x)|>g(x) 或
题型二 含有一个绝对值号不等式的解法
含有一个绝对值号不等式的常见类型及其解法
二、提升新知·注重综合
变式训练
题型二 含有一个绝对值号不等式的解法
解不等式:1<|x-2|≤3.
解:原不等式等价于不等式组
即
解得-1≤x<1或3所以原不等式的解集为[-1,1)∪(3,5].
二、提升新知·注重综合
题型三 含有两个绝对值号的不等式的解法
解析
(1)因为|x-1|>|2x-3|,
所以(x-1)2>(2x-3)2,即(2x-3)2-(x-1)2<0,
所以(2x-3+x-1)(2x-3-x+1)<0,
即(3x-4)(x-2)<0,所以即原不等式的解集为.
例3、解下列不等式:
(1)|x-1|>|2x-3|;
(2)|x-1|+|x-2|>2.
二、提升新知·注重综合
题型三 含有两个绝对值号的不等式的解法
解析
(2)原不等式 或或 或或 x<或x>,
所以原不等式的解集为.
例3、解下列不等式:
(1)|x-1|>|2x-3|;
(2)|x-1|+|x-2|>2.
二、提升新知·注重综合
方法总结
题型三 含有两个绝对值号的不等式的解法
1.含绝对值不等式|x|a的解法
(1)
(2)
2.|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法
(1)|ax+b|≤c -c≤ax+b≤c.
(2)|ax+b|≥c ax+b≥c或ax+b≤-c.
二、提升新知·注重综合
方法总结
题型三 含有两个绝对值号的不等式的解法
3.求解|f(x)|>|g(x)|或|f(x)|<|g(x)|型不等式的方法为平方法,如典例3(1).
4.|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的2种解法
(1)利用绝对值不等式的几何意义.
(2)利用x-a=0,x-b=0的解,将数轴分成三个区间,然后在每个区间上将原不等式转化为不含绝对值的不等式而解之.
变式训练
二、提升新知·注重综合
题型三 含有两个绝对值号的不等式的解法
1.不等式|x+3|-|x-3|>3的解集是 ( )
A. B.
C.{x|x≥3} D.{x|-3解析:当x<-3时,-(x+3)+(x-3)>3,-6>3,无解.
当-3≤x≤3时,x+3+x-3>3,所以x> ,故当x>3时,x+3-(x-3)>3,6>3,
所以x>3.
综上可知,原不等式的解集为.
A
变式训练
二、提升新知·注重综合
题型三 含有两个绝对值号的不等式的解法
2.解不等式|2x-1|<|x|+1.
解析:当x<0时,原不等式可化为-2x+1<-x+1,
解得x>0,又因为x<0,
所以这样的x不存在.
当0≤x<时,原不等式可化为-2x+1解得x>0,又因为0≤x<,所以0当x≥时,原不等式可化为2x-1解得x<2,又因为x≥,
所以≤x<2.
综上所述,原不等式的解集为(0,2).
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
C
1.不等式组的解集在数轴上表示为 ( )
解析:解不等式2x-1≥5,得x≥3.解不等式8-4x<0,得x>2.故不等式组的解集为[3,+∞).选C.
当堂练习
三、训练素养·注重应用、创新
2.不等式3≤|5-2x|<9的解集为 ( )
A.[-2,1)∪[4,7) B.(-2,1]∪(4,7]
C.[-2,1]∪[4,7) D.(-2,1]∪[4,7)
D
解析:因为|5-2x|=|2x-5|,则原不等式等价于3≤2x-5<9或-9<2x-5≤-3,
解得4≤x<7或-23.不等式|x-2|≤|x|的解集是____________.
解析:|x-2|≤|x| (x-2)2≤x2 4-4x≤0 x≥1.
{x|x≥1}
当堂练习
三、训练素养·注重应用、创新
4.不等式组的解集为______________.
解析:记原不等式组为
解不等式①,得x≤1.
解不等式②,得x≥-4.
故原不等式组的解集为[-4,1].
[-4,1]
当堂练习
三、训练素养·注重应用、创新
5.已知关于x的不等式组的解集是(5,22),则a =________,b=________.
解析:记原不等式组为
解不等式①,得x<.
解不等式②,得x>.
因为原不等式组的解集为(5,22),
所以
解这个关于a,b的二元一次方程组,得
3
5
当堂练习
二、创新应用题
三、训练素养·注重应用、创新
6.已知关于x的不等式组无解,求a的取值范围.
解析:解不等式①,得x≤3.
解不等式②,得x>a.
因为该不等式组无解,
所以不等式①和②的解集在数轴上的表示如图所示.
所以a>3.
当a=3时,代入不等式组,得x≤3,且x>3,
此时,不等式组也无解,满足题意.
所以,a的取值范围为[3,+∞).
2.2 不等式
第二章 等式与不等式
2.2.2 不等式的解集
学习目标
1.梳理不等式的解集.
2.会解一元一次不等式组.
3.会解简单的绝对值不等式.
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
不等式的解集 数学抽象 水平1 水平2 不等式的解集是继不等式性质后的一个重要章节,求解不等式的解集必须熟练掌握不等式基本性质,同时注意在解不等式时必须是进行同解变形。要掌握不等式、不等式组解集的求法以及绝对不值等式的解集的求法。 【考查内容】在高考中,不等式的解集是必考内容,特别是不等式解法,绝对值不等式的解法,常与其他知识结合起来考查,因此其解集的求法是常考的题型。
【考查题型】填空题、选择题,绝对值不等式的解法常见于解答题中
【分值情况】5~15分
不等式组的解集 数学推理 水平1 水平2 绝对值不等式 数学抽象 水平1 水平2 绝对值不等式的解法 数学运算 水平1 水平2 知识点一 不等式的解集与不等式组的解集
(一)教材梳理填空
一、自学教材·注重基础
(1)不等式的解集
一般地,不等式的________组成的集合称为不等式的解集.
(2)不等式组的解集
对于由若干个不等式联立得到的不等式组来说,这些不等式的解集的________称为不等式组的解集.
(二)基本知能小试
一、自学教材·注重基础
1.判断正误
(1)不等式-2x+1>0的解集为. ( )
(2)ax+b>0的解集为. ( )
×
知识点一 不等式的解集与不等式组的解集
×
2.不等式3x-5<0的解集为________.
解析:由3x-5<0,得3x<5,即x<.
(二)基本知能小试
一、自学教材·注重基础
知识点一 不等式的解集与不等式组的解集
3.不等式组的解集为________.
解析:由2x-1>0,得x>;由x+1<3,得x<2.
∴不等式组的解集为.
知识点二 绝对值不等式
(一)教材梳理填空
一、自学教材·注重基础
(1)绝对值不等式
一般地,含有_________的不等式称为绝对值不等式.
(2)数轴上两点间的距离公式及中点坐标公式
一般地,如果实数a,b在数轴上对应的点分别为A,B,即A(a),B(b),则线段AB的长为|AB|= _________ ,线段AB的中点M对应的数x= _________.
(二)基本知能小试
一、自学教材·注重基础
×
√
×
知识点二 绝对值不等式
1.判断正误
(1)不等式|x|<2的解集为(-2,2). ( )
(2)不等式|x|
(4)若|a|>|b|,则a>b. ( )
×
(二)基本知能小试
一、自学教材·注重基础
知识点二 绝对值不等式
2.不等式|2x-1|<5的解集为___________.
解析:由|2x-1|<5,得-5<2x-1<5,即-4<2x<6,∴-2
3.不等式|x-2|>3的解集为_________________.
解析:∵|x-2|>3,
∴x-2>3或x-2<-3,
即x>5或x<-1.
(-∞,-1)∪(5,+∞)
(二)基本知能小试
一、自学教材·注重基础
6
知识点二 绝对值不等式
1
4.数轴上两点A(4),B(-2),则|AB|=________,AB的中点M的坐标为________.
解析:|AB|=|4-(-2)|=6,=1.
题型一 不等式的解法
例1、解下列不等式组:
(1)
(2)
解析
二、提升新知·注重综合
(1)解不等式①,得x<-6,解不等式②,得x≥2.把不等式①和②的解集在数轴上表示出来:
由图可知,解集没有公共部分,不等式组无解,即不等式组的解集为.
.
题型一 不等式的解法
例1、解下列不等式组:
(1)
(2)
解析
二、提升新知·注重综合
(2)解不等式①,得x>-,解不等式②,得x≤,把不等式①和②的解集在数轴上表示出来:
由图可知,不等式组的解集为.
方法总结
二、提升新知·注重综合
(1)求出不等式组中每个不等式的解集;
(2)借助数轴找出各解集的公共部分;
(3)写出不等式组的解集.
解不等式组的三个步骤
题型一 不等式的解法
变式训练
二、提升新知·注重综合
题型一 不等式的解法
1.解不等式组:-1<≤5.
解析:法一:原不等式组可化为下面的不等式组
解不等式①,得x>-1.
解不等式②,得x≤8.
所以不等式组的解集为(-1,8].
法二:由-1<≤5,
可得-3<2x-1≤15,
即-2<2x≤16,
解得-1
变式训练
二、提升新知·注重综合
题型一 不等式的解法
2.已知关于x的不等式组的解集为(1,3),求a的值.
解析:由2x+1>3,得x>1,
由a-x>1,得x
∴a-1=3,即a=4.
二、提升新知·注重综合
题型二 含有一个绝对值号不等式的解法
解析
(1)原不等式等价于-7<2x+5<7,
所以-12<2x<2,
所以-6
可得2x+5>7+x或2x+5<-(7+x),
所以x>2或x<-4,
所以原不等式的解集为(-∞,-4)∪(2,+∞).
例2、解下列不等式:
(1)|2x+5|<7;
(2)|2x+5|>7+x;
(3)2≤|x-2|≤4.
二、提升新知·注重综合
题型二 含有一个绝对值号不等式的解法
解析
(3)原不等式等价于
由①得x-2≤-2或x-2≥2,
所以x≤0或x≥4.
例2、解下列不等式:
(1)|2x+5|<7;
(2)|2x+5|>7+x;
(3)2≤|x-2|≤4.
二、提升新知·注重综合
方法总结
(1)求形如|f(x)|
(2)求形如|f(x)|
①等价转化法:
|f(x)|
(这里g(x)可正也可负)
②分类讨论法:
|f(x)|
题型二 含有一个绝对值号不等式的解法
含有一个绝对值号不等式的常见类型及其解法
二、提升新知·注重综合
变式训练
题型二 含有一个绝对值号不等式的解法
解不等式:1<|x-2|≤3.
解:原不等式等价于不等式组
即
解得-1≤x<1或3
二、提升新知·注重综合
题型三 含有两个绝对值号的不等式的解法
解析
(1)因为|x-1|>|2x-3|,
所以(x-1)2>(2x-3)2,即(2x-3)2-(x-1)2<0,
所以(2x-3+x-1)(2x-3-x+1)<0,
即(3x-4)(x-2)<0,所以
例3、解下列不等式:
(1)|x-1|>|2x-3|;
(2)|x-1|+|x-2|>2.
二、提升新知·注重综合
题型三 含有两个绝对值号的不等式的解法
解析
(2)原不等式 或或 或或 x<或x>,
所以原不等式的解集为.
例3、解下列不等式:
(1)|x-1|>|2x-3|;
(2)|x-1|+|x-2|>2.
二、提升新知·注重综合
方法总结
题型三 含有两个绝对值号的不等式的解法
1.含绝对值不等式|x|
(1)
(2)
2.|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法
(1)|ax+b|≤c -c≤ax+b≤c.
(2)|ax+b|≥c ax+b≥c或ax+b≤-c.
二、提升新知·注重综合
方法总结
题型三 含有两个绝对值号的不等式的解法
3.求解|f(x)|>|g(x)|或|f(x)|<|g(x)|型不等式的方法为平方法,如典例3(1).
4.|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的2种解法
(1)利用绝对值不等式的几何意义.
(2)利用x-a=0,x-b=0的解,将数轴分成三个区间,然后在每个区间上将原不等式转化为不含绝对值的不等式而解之.
变式训练
二、提升新知·注重综合
题型三 含有两个绝对值号的不等式的解法
1.不等式|x+3|-|x-3|>3的解集是 ( )
A. B.
C.{x|x≥3} D.{x|-3
当-3≤x≤3时,x+3+x-3>3,所以x> ,故
所以x>3.
综上可知,原不等式的解集为.
A
变式训练
二、提升新知·注重综合
题型三 含有两个绝对值号的不等式的解法
2.解不等式|2x-1|<|x|+1.
解析:当x<0时,原不等式可化为-2x+1<-x+1,
解得x>0,又因为x<0,
所以这样的x不存在.
当0≤x<时,原不等式可化为-2x+1
所以≤x<2.
综上所述,原不等式的解集为(0,2).
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
C
1.不等式组的解集在数轴上表示为 ( )
解析:解不等式2x-1≥5,得x≥3.解不等式8-4x<0,得x>2.故不等式组的解集为[3,+∞).选C.
当堂练习
三、训练素养·注重应用、创新
2.不等式3≤|5-2x|<9的解集为 ( )
A.[-2,1)∪[4,7) B.(-2,1]∪(4,7]
C.[-2,1]∪[4,7) D.(-2,1]∪[4,7)
D
解析:因为|5-2x|=|2x-5|,则原不等式等价于3≤2x-5<9或-9<2x-5≤-3,
解得4≤x<7或-2
解析:|x-2|≤|x| (x-2)2≤x2 4-4x≤0 x≥1.
{x|x≥1}
当堂练习
三、训练素养·注重应用、创新
4.不等式组的解集为______________.
解析:记原不等式组为
解不等式①,得x≤1.
解不等式②,得x≥-4.
故原不等式组的解集为[-4,1].
[-4,1]
当堂练习
三、训练素养·注重应用、创新
5.已知关于x的不等式组的解集是(5,22),则a =________,b=________.
解析:记原不等式组为
解不等式①,得x<.
解不等式②,得x>.
因为原不等式组的解集为(5,22),
所以
解这个关于a,b的二元一次方程组,得
3
5
当堂练习
二、创新应用题
三、训练素养·注重应用、创新
6.已知关于x的不等式组无解,求a的取值范围.
解析:解不等式①,得x≤3.
解不等式②,得x>a.
因为该不等式组无解,
所以不等式①和②的解集在数轴上的表示如图所示.
所以a>3.
当a=3时,代入不等式组,得x≤3,且x>3,
此时,不等式组也无解,满足题意.
所以,a的取值范围为[3,+∞).
