人教B版高中数学必修第一册 2.2.3 《一元二次不等式的解法》(共25张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册 2.2.3 《一元二次不等式的解法》(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 785.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 22:14:46 | ||
图片预览








文档简介
(共25张PPT)
2.2.3 一元二次不等式的解法
第二章 等式与不等式
2.2 不等式
学习目标
1.经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义,
2.能借助一元二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集。
学习目标
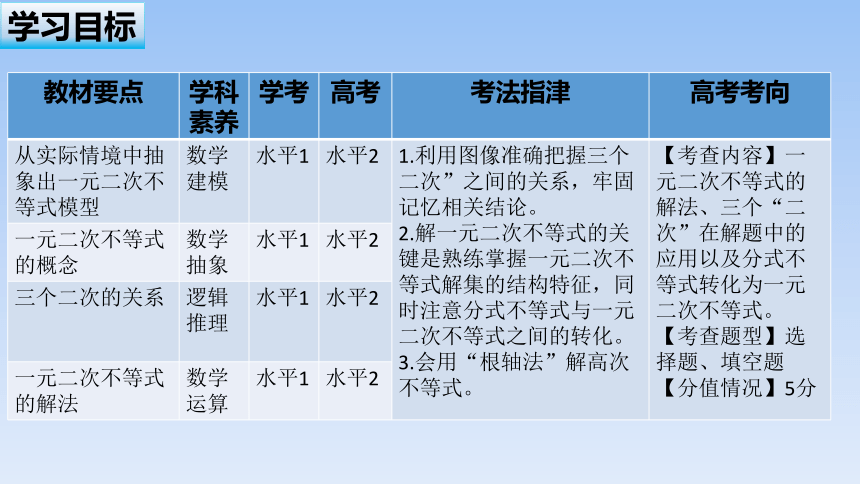
教材要点 学科素养 学考 高考 考法指津 高考考向
从实际情境中抽象出一元二次不等式模型 数学建模 水平1 水平2 1.利用图像准确把握三个二次”之间的关系,牢固记忆相关结论。 2.解一元二次不等式的关键是熟练掌握一元二次不等式解集的结构特征,同时注意分式不等式与一元二次不等式之间的转化。 3.会用“根轴法”解高次不等式。 【考查内容】一元二次不等式的解法、三个“二次”在解题中的应用以及分式不等式转化为一元二次不等式。
【考查题型】选择题、填空题
【分值情况】5分
一元二次不等式的概念 数学抽象 水平1 水平2 三个二次的关系 逻辑推理 水平1 水平2 一元二次不等式的解法 数学运算 水平1 水平2 知识点一 一元二次不等式的解法
(一)教材梳理填空
一、自学教材·注重基础
(1)一元二次不等式的概念
一般的,形如____________的不等式称为一元二次不等式,其中a,b,c是常数,而且a≠0.
(2)因式分解法解一元二次不等式
一般地,如果x10的解集是(-∞,x1)∪(x2,+∞).
知识点一 一元二次不等式的解法
(一)教材梳理填空
一、自学教材·注重基础
(3)配方法解一元二次不等式
一元二次不等式ax2+bx+c>0(a≠0)通过配方总是可以变为_________或_________的形式,然后根据k的正负等知识,就可以得到原不等式的解集.
(二)基本知能小试
√
×
×
一、自学教材·注重基础
知识点一 一元二次不等式的解法
1.判断正误
(1)mx2-5x<0是一元二次不等式. ( )
(2)若a>0,则一元二次不等式ax2+1>0无解. ( )
(3)不等式x2-2x+3>0的解集为R. ( )
2.不等式x2-6x-1≤0的解集为_______________.
3.x2+4x+1≥0的解集为______________________ .
(二)基本知能小试
一、自学教材·注重基础
知识点一 一元二次不等式的解法
4.求不等式-2x2+4x+5>0的解集.
解析:原不等式可化为2x2-4x-5<0,
因为2x2-4x-5=2(x-1)2-7.
所以原不等式可化为2(x-1)2-7<0,
即(x-1)2<,
解得--题型一 因式分解法解一元二次不等式
解析
二、提升新知·注重综合
例1、用因式分解法解下列不等式:
(1)6x2+5x+1>0;
(2)6x2+11x-7<0;
(3)-42x2+33x-6≥0.
(1)由6x2+5x+1>0,得(2x+1)(3x+1)>0,
∴x>或x<,
∴不等式的解集为.
(2)由6x2+11x-7<0,得(2x-1)(3x+7)<0,
∴,
∴不等式的解集为.
题型一 因式分解法解一元二次不等式
解析
二、提升新知·注重综合
例1、用因式分解法解下列不等式:
(1)6x2+5x+1>0;
(2)6x2+11x-7<0;
(3)-42x2+33x-6≥0.
(3)由-42x2+33x-6≥0,得42x2-33x+6≤0,
即(6x-3)(7x-2)≤0,
,
∴不等式的解集为.
方法总结
二、提升新知·注重综合
题型一 因式分解法解一元二次不等式
利用因式分解法求解一元二次不等式ax2+bx+c>0(<0)的解集时,其关键是利用“十字相乘法”分解因式,同时要注意a的符号.
变式训练
二、提升新知·注重综合
题型一 因式分解法解一元二次不等式
解不等式:-3x2-2x+8≥0.
解析:原不等式可化为3x2+2x-8≤0,
即(3x-4)(x+2)≤0,
解得-2≤x≤,
∴原不等式的解集为.
解析
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
例2、用配方法解下列不等式:
(1)x2-4x-1≥0;
(2)(x+1)(x-7)≤2.
(1)∵x2-4x-1=(x-2)2-5,
∴原不等式可化为(x-2)2-5≥0,
∴(x-2)2≥5,
即x-2≥或x-2≤- ,
解得x≥2+ 或x≤2- ,
∴不等式的解集为(-∞,2- ]∪[2+ ,+∞).
解析
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
例2、用配方法解下列不等式:
(1)x2-4x-1≥0;
(2)(x+1)(x-7)≤2.
(2)由(x+1)(x-7)≤2,得x2-6x-9≤0.
又x2-6x-9=(x-3)2-18,
∴原不等式化为(x-3)2-18≤0,
∴(x-3)2≤18,
即-3≤x-3≤3 ,
解得3-3 ≤x≤3+3 ,
∴不等式的解集为[3-3 ,3+3 ].
方法总结
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
用配方法解一元二次不等式ax2+bx+c>0(a≠0)的解集时,首先将x2的系数转化为正值,然后配方成a(x-h)2>k或a(x-h)2变式训练
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
1.方程x2+4x-7>0的解集为___________________________.
解析:∵x2+4x-7=(x+2)2-11,
∴原不等式化为(x+2)2-11>0,
即(x+2)2>11,
∴x+2>或x+2<- ,
∴x>-2+ 或x<-2- ,
∴原不等式的解集为(-∞,-2- )∪(-2+ ,+∞).
(-∞,-2- )∪(-2+ ,+∞)
变式训练
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
2.解下列不等式:
(1)3x2-6x+2>0;
(2)-x2+x- >0.
解析:(1)3x2-6x+2>0可化为x2-2x+>0.
又∵x2-2x+ =(x-1)2- ,
∴原不等式化为(x-1)2> ,
∴x-1>或x-1<- ,即x>1+ 或x<1- ,
∴原不等式的解集为.
变式训练
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
2.解下列不等式:
(1)3x2-6x+2>0;
(2)-x2+x- >0.
解析:(2)由,得,
配方得,
,
即,
∴不等式的解集为.
解析
二、提升新知·注重综合
题型三 解简单的分式不等式
例3、解下列不等式:
(1) ;(2) .
(1)由,得>0,此不等式等价于(x+2)(x-1)>0,∴原不等式的解集为(-∞,-2)∪(1,+∞).
(2)法一:移项得-2≤0,左边通分并化简有≤0,即≥0,它的同解不等式为
∴x<2或x≥5.
∴原不等式的解集为(-∞,2)∪[5,+∞).
解析
二、提升新知·注重综合
题型三 解简单的分式不等式
例3、解下列不等式:
(1) ;(2) .
法二:原不等式可化为≥0,
此不等式等价于①
或②
解①得x≥5,解②得x<2,
∴原不等式的解集为(-∞,2)∪[5,+∞).
方法总结
二、提升新知·注重综合
题型三 解简单的分式不等式
对于比较简单的分式不等式,可直接转化为一元二次不等式或一元一次不等式组求解,但要注意分母不为零.对于不等号右边不为零的较复杂的分式不等式,先移项再通分(不要去分母),使之转化为不等号右边为零,然后再用上述方法求解.
变式训练
二、提升新知·注重综合
题型三 解简单的分式不等式
解下列不等式:
(1) ;(2).
解析:(1)原不等式等价于
即.
∴原不等式的解集为[-2,3).
(2)原不等式可化为,即.
等价于(3x-2)(4x-3)<0,∴.
∴原不等式的解集为.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
1.不等式(x+2)(x-3)<6的解集为________.
解析:原不等式可化为x2-x-12<0,即(x+3)(x-4)<0,
于是或解得-3所以原不等式的解集为(-3,4).
(-3,4)
2.不等式-x2+8x-3>0的解集为_______________.
解析:由-x2+8x-3>0,得x2-8x+3<0,
配方得,(x-4)2<13,所以,
即4-所以原不等式的解集为{x|4- 当堂练习
一、基础经典题
三、训练素养·注重应用、创新
3.不等式16-8x+x2≤0的解集为______________.
解析:16-8x+x20,即(x-4)20,∴x=4.
∴不等式的解集为{4}.
{4}
4.解下列不等式:
(1) ;(2) .
解析:(1) .
∴原不等式的解集为.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
4.解下列不等式:
(1) ;(2) .
解析:(2)法一:原不等式可化为或或.
∴原不等式的解集为.
法二:原不等式可化为.
∴原不等式的解集为.
当堂练习
二、创新应用题
三、训练素养·注重应用、创新
5.解关于x的不等式x2-3ax-18a2>0.
解:将x2-3ax-18a2>0变形得(x-6a)(x+3a)>0,
方程(x-6a)(x+3a)=0的两根为6a,-3a.
所以当a>0时,6a>-3a,原不等式的解集为{x|x<-3a或x>6a};
当a=0时,6a=-3a=0,原不等式的解集为{x|x≠0};
当a<0时,6a<-3a,原不等式的解集为{x|x<6a或x>-3a}.
2.2.3 一元二次不等式的解法
第二章 等式与不等式
2.2 不等式
学习目标
1.经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义,
2.能借助一元二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集。
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
从实际情境中抽象出一元二次不等式模型 数学建模 水平1 水平2 1.利用图像准确把握三个二次”之间的关系,牢固记忆相关结论。 2.解一元二次不等式的关键是熟练掌握一元二次不等式解集的结构特征,同时注意分式不等式与一元二次不等式之间的转化。 3.会用“根轴法”解高次不等式。 【考查内容】一元二次不等式的解法、三个“二次”在解题中的应用以及分式不等式转化为一元二次不等式。
【考查题型】选择题、填空题
【分值情况】5分
一元二次不等式的概念 数学抽象 水平1 水平2 三个二次的关系 逻辑推理 水平1 水平2 一元二次不等式的解法 数学运算 水平1 水平2 知识点一 一元二次不等式的解法
(一)教材梳理填空
一、自学教材·注重基础
(1)一元二次不等式的概念
一般的,形如____________的不等式称为一元二次不等式,其中a,b,c是常数,而且a≠0.
(2)因式分解法解一元二次不等式
一般地,如果x1
知识点一 一元二次不等式的解法
(一)教材梳理填空
一、自学教材·注重基础
(3)配方法解一元二次不等式
一元二次不等式ax2+bx+c>0(a≠0)通过配方总是可以变为_________或_________的形式,然后根据k的正负等知识,就可以得到原不等式的解集.
(二)基本知能小试
√
×
×
一、自学教材·注重基础
知识点一 一元二次不等式的解法
1.判断正误
(1)mx2-5x<0是一元二次不等式. ( )
(2)若a>0,则一元二次不等式ax2+1>0无解. ( )
(3)不等式x2-2x+3>0的解集为R. ( )
2.不等式x2-6x-1≤0的解集为_______________.
3.x2+4x+1≥0的解集为______________________ .
(二)基本知能小试
一、自学教材·注重基础
知识点一 一元二次不等式的解法
4.求不等式-2x2+4x+5>0的解集.
解析:原不等式可化为2x2-4x-5<0,
因为2x2-4x-5=2(x-1)2-7.
所以原不等式可化为2(x-1)2-7<0,
即(x-1)2<,
解得-
解析
二、提升新知·注重综合
例1、用因式分解法解下列不等式:
(1)6x2+5x+1>0;
(2)6x2+11x-7<0;
(3)-42x2+33x-6≥0.
(1)由6x2+5x+1>0,得(2x+1)(3x+1)>0,
∴x>或x<,
∴不等式的解集为.
(2)由6x2+11x-7<0,得(2x-1)(3x+7)<0,
∴,
∴不等式的解集为.
题型一 因式分解法解一元二次不等式
解析
二、提升新知·注重综合
例1、用因式分解法解下列不等式:
(1)6x2+5x+1>0;
(2)6x2+11x-7<0;
(3)-42x2+33x-6≥0.
(3)由-42x2+33x-6≥0,得42x2-33x+6≤0,
即(6x-3)(7x-2)≤0,
,
∴不等式的解集为.
方法总结
二、提升新知·注重综合
题型一 因式分解法解一元二次不等式
利用因式分解法求解一元二次不等式ax2+bx+c>0(<0)的解集时,其关键是利用“十字相乘法”分解因式,同时要注意a的符号.
变式训练
二、提升新知·注重综合
题型一 因式分解法解一元二次不等式
解不等式:-3x2-2x+8≥0.
解析:原不等式可化为3x2+2x-8≤0,
即(3x-4)(x+2)≤0,
解得-2≤x≤,
∴原不等式的解集为.
解析
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
例2、用配方法解下列不等式:
(1)x2-4x-1≥0;
(2)(x+1)(x-7)≤2.
(1)∵x2-4x-1=(x-2)2-5,
∴原不等式可化为(x-2)2-5≥0,
∴(x-2)2≥5,
即x-2≥或x-2≤- ,
解得x≥2+ 或x≤2- ,
∴不等式的解集为(-∞,2- ]∪[2+ ,+∞).
解析
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
例2、用配方法解下列不等式:
(1)x2-4x-1≥0;
(2)(x+1)(x-7)≤2.
(2)由(x+1)(x-7)≤2,得x2-6x-9≤0.
又x2-6x-9=(x-3)2-18,
∴原不等式化为(x-3)2-18≤0,
∴(x-3)2≤18,
即-3≤x-3≤3 ,
解得3-3 ≤x≤3+3 ,
∴不等式的解集为[3-3 ,3+3 ].
方法总结
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
用配方法解一元二次不等式ax2+bx+c>0(a≠0)的解集时,首先将x2的系数转化为正值,然后配方成a(x-h)2>k或a(x-h)2
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
1.方程x2+4x-7>0的解集为___________________________.
解析:∵x2+4x-7=(x+2)2-11,
∴原不等式化为(x+2)2-11>0,
即(x+2)2>11,
∴x+2>或x+2<- ,
∴x>-2+ 或x<-2- ,
∴原不等式的解集为(-∞,-2- )∪(-2+ ,+∞).
(-∞,-2- )∪(-2+ ,+∞)
变式训练
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
2.解下列不等式:
(1)3x2-6x+2>0;
(2)-x2+x- >0.
解析:(1)3x2-6x+2>0可化为x2-2x+>0.
又∵x2-2x+ =(x-1)2- ,
∴原不等式化为(x-1)2> ,
∴x-1>或x-1<- ,即x>1+ 或x<1- ,
∴原不等式的解集为.
变式训练
二、提升新知·注重综合
题型二 用配方法解一元二次不等式
2.解下列不等式:
(1)3x2-6x+2>0;
(2)-x2+x- >0.
解析:(2)由,得,
配方得,
,
即,
∴不等式的解集为.
解析
二、提升新知·注重综合
题型三 解简单的分式不等式
例3、解下列不等式:
(1) ;(2) .
(1)由,得>0,此不等式等价于(x+2)(x-1)>0,∴原不等式的解集为(-∞,-2)∪(1,+∞).
(2)法一:移项得-2≤0,左边通分并化简有≤0,即≥0,它的同解不等式为
∴x<2或x≥5.
∴原不等式的解集为(-∞,2)∪[5,+∞).
解析
二、提升新知·注重综合
题型三 解简单的分式不等式
例3、解下列不等式:
(1) ;(2) .
法二:原不等式可化为≥0,
此不等式等价于①
或②
解①得x≥5,解②得x<2,
∴原不等式的解集为(-∞,2)∪[5,+∞).
方法总结
二、提升新知·注重综合
题型三 解简单的分式不等式
对于比较简单的分式不等式,可直接转化为一元二次不等式或一元一次不等式组求解,但要注意分母不为零.对于不等号右边不为零的较复杂的分式不等式,先移项再通分(不要去分母),使之转化为不等号右边为零,然后再用上述方法求解.
变式训练
二、提升新知·注重综合
题型三 解简单的分式不等式
解下列不等式:
(1) ;(2).
解析:(1)原不等式等价于
即.
∴原不等式的解集为[-2,3).
(2)原不等式可化为,即.
等价于(3x-2)(4x-3)<0,∴.
∴原不等式的解集为.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
1.不等式(x+2)(x-3)<6的解集为________.
解析:原不等式可化为x2-x-12<0,即(x+3)(x-4)<0,
于是或解得-3
(-3,4)
2.不等式-x2+8x-3>0的解集为_______________.
解析:由-x2+8x-3>0,得x2-8x+3<0,
配方得,(x-4)2<13,所以,
即4-
一、基础经典题
三、训练素养·注重应用、创新
3.不等式16-8x+x2≤0的解集为______________.
解析:16-8x+x20,即(x-4)20,∴x=4.
∴不等式的解集为{4}.
{4}
4.解下列不等式:
(1) ;(2) .
解析:(1) .
∴原不等式的解集为.
当堂练习
一、基础经典题
三、训练素养·注重应用、创新
4.解下列不等式:
(1) ;(2) .
解析:(2)法一:原不等式可化为或或.
∴原不等式的解集为.
法二:原不等式可化为.
∴原不等式的解集为.
当堂练习
二、创新应用题
三、训练素养·注重应用、创新
5.解关于x的不等式x2-3ax-18a2>0.
解:将x2-3ax-18a2>0变形得(x-6a)(x+3a)>0,
方程(x-6a)(x+3a)=0的两根为6a,-3a.
所以当a>0时,6a>-3a,原不等式的解集为{x|x<-3a或x>6a};
当a=0时,6a=-3a=0,原不等式的解集为{x|x≠0};
当a<0时,6a<-3a,原不等式的解集为{x|x<6a或x>-3a}.
