人教版选择性必修二 1.4 质谱仪专题(含答案)
文档属性
| 名称 | 人教版选择性必修二 1.4 质谱仪专题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-06 18:58:01 | ||
图片预览


文档简介
人教版选择性必修二第一章质谱仪专题(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
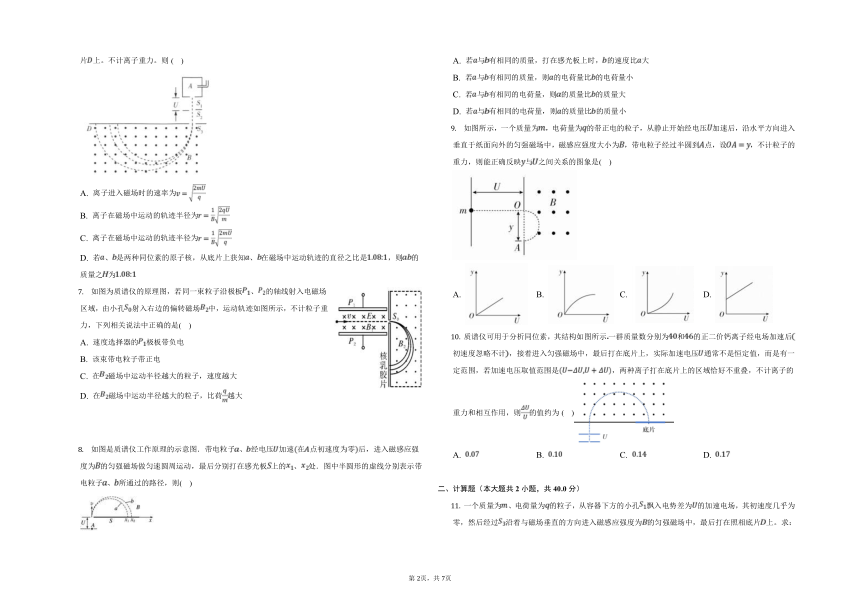
1. 如图所示,在容器中有同一种元素的两种同位素正粒子,它们的初速度几乎为,粒子可从容器下方的小孔飘入加速电场,然后经过沿着与磁场垂直的方向进入匀强磁场中,最后第一种同位素粒子打到照相底片上的点,第二种同位素粒子打到照相底片上的点。不计同位素粒子重力。量出点、点到的距离分别为、,则第一种与第二种同位素粒子在磁场中运动的时间之比为( )
A. B. C. D.
2. 如图所示,含有、、的带电粒子束从小孔处射入速度选择器,沿直线运动的粒子在小孔处射出后垂直进入偏转磁场,最终打在、两点则( )
A. 打在点的粒子是 B. 的长度是长度的倍
C. 粒子在偏转磁场中运动的时间都相等 D. 只有比荷相同的、才能进入偏转磁场
3. 如图所示,为质谱仪的工作原理示意图,速度选择器内相互正交的匀强磁场和匀强电场的强度分别为和。平板上有可让粒子通过的狭缝和记录粒子位置的胶片,平板下方有磁感应强度为的匀强磁场。下列说法正确的是( )
A. 速度选择器中的磁场方向垂直纸面向里
B. 能通过狭缝的带电粒子的速率等于
C. 图中打在胶片上的粒子带负电
D. 粒子打在胶片上的位置越靠近狭缝,粒子的比荷越小
4. 某一个带有速度选择器的质谱仪原理如图所示,为粒子加速器,加速电压为;为速度选择器,磁场方向垂直纸面向里,磁感应强度为;的两板间距离为,电场方向向左或向右未知;为偏转分离器,磁感应强度为。今有一质量为、电荷量为的粒子不计重力,经加速后,该粒子恰能沿直线通过速度选择器,然后进入分离器做匀速圆周运动,下列分析正确的是( )
A. 该粒子不一定带正电
B. 区域中电场方向可能向右
C. 增大并相应减小,粒子才可能仍然沿直线通过
D. 增大并相应改变,使粒子仍然沿直线通过,在中的半径可能不变
5. 如图为一质谱仪的原理图,粒子源中有大量电量均为而质量不同的带电粒子,从进入间的加速电场,加速后进入电场强度和磁感应强度恒定不变的速度选择器间,能通过狭缝的粒子竖直向下垂直进入磁感应强度为的匀强磁场中,偏转后打到水平照相底片上形成谱线。若粒子在匀强磁场中的偏转距离为,不计粒子重力,则与的关系式为( )
A. B. C. D.
6. 图示装置叫质谱仪,最初是由阿斯顿设计的,是一种测量带电粒子的质量和分析同位素的重要工具。其工作原理如下:一个质量为、电荷量为的离子,从容器下方的小孔飘入电势差为的加速电场,其初速度几乎为零,然后经过沿着与磁场垂直的方向,进入磁感应强度为的匀强磁场中,最后打到底片上。不计离子重力。则( )
A. 离子进入磁场时的速率为
B. 离子在磁场中运动的轨迹半径为
C. 离子在磁场中运动的轨迹半径为
D. 若、是两种同位素的原子核,从底片上获知、在磁场中运动轨迹的直径之比是,则的质量之为
7. 如图为质谱仪的原理图,若同一束粒子沿极板、的轴线射入电磁场区域,由小孔射入右边的偏转磁场中,运动轨迹如图所示,不计粒子重力,下列相关说法中正确的是( )
A. 速度选择器的极板带负电
B. 该束带电粒子带正电
C. 在磁场中运动半径越大的粒子,速度越大
D. 在磁场中运动半径越大的粒子,比荷越大
8. 如图是质谱仪工作原理的示意图.带电粒子、经电压加速在点初速度为零后,进入磁感应强度为的匀强磁场做匀速圆周运动,最后分别打在感光板上的、处.图中半圆形的虚线分别表示带电粒子、所通过的路径,则( )
A. 若与有相同的质量,打在感光板上时,的速度比大
B. 若与有相同的质量,则的电荷量比的电荷量小
C. 若与有相同的电荷量,则的质量比的质量大
D. 若与有相同的电荷量,则的质量比的质量小
9. 如图所示,一个质量为,电荷量为的带正电的粒子,从静止开始经电压加速后,沿水平方向进入垂直于纸面向外的匀强磁场中,磁感应强度大小为,带电粒子经过半圆到点,设,不计粒子的重力,则能正确反映与之间关系的图象是( )
A. B. C. D.
10. 质谱仪可用于分析同位素,其结构如图所示一群质量数分别为和的正二价钙离子经电场加速后初速度忽略不计,接着进入匀强磁场中,最后打在底片上,实际加速电压通常不是恒定值,而是有一定范围,若加速电压取值范围是,两种离子打在底片上的区域恰好不重叠,不计离子的重力和相互作用,则的值约为( )
A. B. C. D.
二、计算题(本大题共2小题,共40.0分)
11. 一个质量为、电荷量为的粒子,从容器下方的小孔飘入电势差为的加速电场,其初速度几乎为零,然后经过沿着与磁场垂直的方向进入磁感应强度为的匀强磁场中,最后打在照相底片上。求:
粒子进入磁场时的速率。
粒子在磁场中运动的轨道半径。
如图所示为质谱仪的构造原理图,它是一种分离和检测不同同位素的重要工具。质子数相同而中子数不同的同一元素的不同核素互称为同位素。现让待测的不同带电粒子经加速电场后进入速度选择器,速度选择器的平行金属板之间有相互正交的匀强磁场和匀强电场图中未画出,磁感应强度为,电场强度为,金属板板,在平板上有可让粒子通过的狭缝,带电粒子经过速度选择器后,立即从点沿垂直平板且垂直于磁场方向的速度进入磁感应强度为、并以平板为边界的有界匀强磁场中,在磁场中偏转后打在记录它的照相底片上,底片厚度可忽略不计,且与平板重合。根据粒子打在底片上的位置,便可以对它的比荷电荷量与质量之比情况进行分析。在下面的讨论中,磁感应强度为的匀强磁场区域足够大,空气阻力、带电粒子所受的重力及它们之间的相互作用力均可忽略不计。
带电粒子通过狭缝时的速度大小;
不同的带电粒子经加速电场加速后可获得不同的速率,这些粒子进入速度选择器后,要想使通过狭缝的带电粒子速度大一些,应怎样调整速度选择器的电场强度和磁感应强度的大小;
若用这个质谱仪分别观测氢的两种同位素离子和,它们分别打在照相底片上相距为的两点;若用这个质谱仪相同条件下再分别观测碳的两种同位素离子和,它们分别打在照相底片上相距为的两点。请通过计算说明,与的大小关系;
若氢的两种同位素离子所带电荷量为的质量分别为和,且已知,它们同时从加速电场射出。试分析说明这两种粒子哪一种先到达照相底片,并求出它们到达照相底片上的时间差。
12.
答案和解析
1.【答案】
【解析】
【分析】
粒子在电场中加速,粒子在磁场中作圆周运动,洛伦兹力提供向心力,结合求得粒子在磁场中运动的时间表达式。
本题的关键是熟练周期和半径的表达式,并指导同位素的概念:质子数相同、中子数不同不同相同。
【解答】
设加速电场的电压为,磁场的磁感应强度为,粒子电荷量为、质量为,
在电场中加速过程有:
在磁场中偏转有:
据几何关系有
粒子运动的时间
以上四式联立得:,
所以,,故C正确,ABD错误。
故选C。
2.【答案】
【解析】略
3.【答案】
【解析】
【分析】
根据带电粒子在电场中的加速判断电荷的电性,粒子经过速度选择器时所受的电场力和洛伦兹力平衡,根据平衡求出粒子经过速度选择器的速度,通过带电粒子在磁场中的偏转,根据半径的大小判断粒子比荷的大小。
本题主要考查了质谱仪的结构和工作原理,解决本题的关键知道粒子在速度选择器中做匀速直线运动,在磁场中做匀速圆周运动。
【解答】
A、根据加速电场,可知粒子带正电,则粒子在速度选择器中受到的电场力向右,则洛伦兹力向左,由左手定则可判断磁场方向垂直纸面向外,故A错误;
B、能通过狭缝的带电粒子,经过速度选择器时做直线运动,则:,解得:,故B正确;
C、由图可知,粒子在磁场中运动向左偏转,根据左手定则判定,粒子带正电,故C错误;
D、粒子进入磁场后,据牛顿第二定律可得:,解得:,知粒子打在胶片上的位置越靠近狭缝,则越小,粒子的比荷越大,故D错误;
故选:。
4.【答案】
【解析】解:该粒子在中的磁场中向右偏转,根据左手定则可知,粒子一定带正电,故A错误;
B.粒子做区域做直线运动,则电场力等于洛伦兹力,洛伦兹力向右,则电场力向左,可知电场方向向左,故B错误;
C.增大则粒子进入区域的速度增加,若相应减小,则洛伦兹力与电场力仍可能相等,即粒子可能仍然沿直线通过,故C正确;
D.增大,粒子进入区域的速度增加,并相应改变,使粒子仍然沿直线通过,则粒子进入中的速度也增加,根据可得,可知在中的半径变大,故D错误。
故选:。
粒子经过速度选择器时,所受的电场力和洛伦兹力平衡,根据带电粒子在磁场中的偏转方向判断电荷的电性;根据平衡条件分析电场可能的方向;同时分析改变电压和磁场时变化时粒子的运动情况。
本题考查质谱仪模型,解决本题的关键知道粒子在速度选择器中做匀速直线运动,在磁场中做匀速圆周运动,明确洛伦兹力充当向心力。
5.【答案】
【解析】解:通过速度选择器的粒子满足,可得;进入偏转磁场后,由可得,,故A正确,BCD错误。
故选:。
带电粒子在速度选择器中受电场力和洛伦兹力平衡,做匀速直线运动,进入偏转电场后做匀速圆周运动,根据半径公式得出半径。
解决本题的关键知道粒子在速度选择器和偏转电场中的运动规律,掌握带电粒子在匀强磁场中运动的半径公式。
6.【答案】
【解析】
【分析】
带电粒子在电场中被加速,应用动能定理可以求出粒子的速度.粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的轨道半径.
、互为同位素,所以电荷量相等,由前面结论得出半径与质量之间的关系,然后由题目的条件即可求出.
【解答】
A、粒子在电场中加速,根据动能定理有,解得,故A错误;
、粒子进入磁场,洛伦兹力提供向心力,有,解得,故B错误,C正确;
D、若、是两种同位素的原子核,则他们的电量相同,质量不同,直径之比等于,则质量之比为,故D错误.
故选C.
7.【答案】
【解析】
【分析】
根据带电粒子在磁场中的偏转方向确定带电粒子的正负。根据在速度选择器中电场力和洛伦兹力平衡确定极板的带电情况。在磁场中,根据洛伦兹力提供向心力,求出粒子的轨道半径,即可知道轨迹半径与什么因素有关。
解决本题的关键会根据左手定则判断洛伦兹力的方向,以及知道在速度选择器中,电荷所受的电场力和洛伦兹力平衡,从速度选择器中沿直线飞出的粒子的速度相等。
【解答】
A.在偏转磁场中,磁场垂直向外,粒子向下偏,因此粒子带正电,而在平行金属板间,根据左手定则知,带电粒子所受的洛伦兹力方向竖直向上,则电场力的方向竖直向下,知电场强度的方向竖直向下,所以速度选择器的极板带正电,故A错误;
B.带电粒子在磁场中向下偏转,磁场的方向垂直纸面向外,根据左手定则知,该粒子带正电,故B正确;
进入磁场中的粒子速度是一定的,根据得,,知越大,比荷越小,故CD错误。
故选B。
8.【答案】
【解析】
【分析】
根据动能定理求出粒子出加速电场时的速度,通过洛伦兹力提供向心力,根据牛顿第二定律求出轨道半径的关系式,从而比较、的电量和质量关系。
本题考查了质谱仪的工作原理,要利用动能定理,洛伦兹力提供向心力等知识来解决问题。
【解答】
粒子在电场中加速,由动能定理得:解得:,
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,则,解得:,
根据图像可知粒子的半径小,粒子的半径大,若和质量相同,则的电量小,的速度小,若和的电量相等,因为的半径大,则的质量大,故D正确,ABC错误。
故选D。
9.【答案】
【解析】
【分析】
根据动能定理得到带电粒子加速获得的速度,带电粒子进入磁场中由洛伦兹力提供向心力做匀速圆周运动,由牛顿第二定律得到半径,,根据与的表达式选择图象。
本题主要考查带电粒子在匀强磁场中的运动规律及动能定理的应用。
【解答】
在加速电场中,由动能定理得 ,在磁场中,由 ,得:,则得:,、、都一定,则由数学知识得到,图象是开口向右的抛物线,故B正确,ACD错误。
故选B。
10.【答案】
【解析】
【分析】
两种离子打在底片上的区域恰好不重叠,则质量数为的离子的运动最大半径应等于质量数为的离子的最小半径,由此得解。
本题主要考查质谱仪的工作原理,熟悉其工作原理是解题的关键,有一定难度。
【解答】
正二价钙离子在电场中加速,由动能定理可得:,解得其进入磁场的速度为:,在磁场中离子由洛伦兹力提供向心力:,解得其圆周运动的半径为:。要使两种离子打在底片上的区域恰好不重叠,则需使质量数为的离子的运动最大半径应等于质量数为的离子的最小半径。质量数为的离子在磁场中运动的最大半径为:,质量数为的离子的最小半径为:,由可得:,解得,故A正确。
11.【答案】解:由动能定理得,
解得:
根据
得:
【解析】本题是动能定理和牛顿定律的综合题,解决本题的关键会灵活运用动能定理和牛顿定律。
12.【答案】解:带电粒子在速度选择器中做匀速直线运动,电场力与洛伦兹力平衡:
解得:
由知,要想使通过狭缝的带电粒子速度大一些,可减小或增大。
设的电荷量为,质量为,
在磁感应强度为的磁场中,洛伦兹力提供向心力:
由知
联立解得:
同理,在磁感应强度为的磁场中的轨迹半径
在磁感应强度为的磁场中的轨迹半径
在磁感应强度为的磁场中的轨迹半径
根据几何关系有:
故大于
氢的两种同位素离子同时从加速电场射出后,二者在速度选择器中速度相同,故运动时间相同,
在磁感应强度为的磁场中,质量为的离子的运动时间
又有
洛伦兹力提供向心力:
联立解得:
同理,质量为的离子的运动时间
因为
所以
所以质量为的离子先到达照相底片
它们到达照相底片上的时间差
答:带电粒子通过狭缝时的速度大小为;
不同的带电粒子经加速电场加速后可获得不同的速率,这些粒子进入速度选择器后,要想使通过狭缝的带电粒子速度大一些,可减小或增大;
若用这个质谱仪分别观测氢的两种同位素离子和,它们分别打在照相底片上相距为的两点;若用这个质谱仪相同条件下再分别观测碳的两种同位素离子和,它们分别打在照相底片上相距为的两点。与的大小关系为大于;
若氢的两种同位素离子所带电荷量为的质量分别为和,且已知,它们同时从加速电场射出。质量为的离子先到达照相底片,它们到达照相底片上的时间差为。
【解析】根据带电粒子在速度选择器中做匀速直线运动,电场力与洛伦兹力平衡分析;
根据的计算结果分析;
根据带电粒子在匀强磁场中洛伦兹力提供向心力求出半径,再结合几何关系分析;
根据带电粒子在匀强磁场中洛伦兹力提供向心力求出周期,再结合时间关系分析。
解答本题的关键是知道带电粒子在速度选择器中的速度均相同,在磁场中由洛伦兹力提供向心力。
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
1. 如图所示,在容器中有同一种元素的两种同位素正粒子,它们的初速度几乎为,粒子可从容器下方的小孔飘入加速电场,然后经过沿着与磁场垂直的方向进入匀强磁场中,最后第一种同位素粒子打到照相底片上的点,第二种同位素粒子打到照相底片上的点。不计同位素粒子重力。量出点、点到的距离分别为、,则第一种与第二种同位素粒子在磁场中运动的时间之比为( )
A. B. C. D.
2. 如图所示,含有、、的带电粒子束从小孔处射入速度选择器,沿直线运动的粒子在小孔处射出后垂直进入偏转磁场,最终打在、两点则( )
A. 打在点的粒子是 B. 的长度是长度的倍
C. 粒子在偏转磁场中运动的时间都相等 D. 只有比荷相同的、才能进入偏转磁场
3. 如图所示,为质谱仪的工作原理示意图,速度选择器内相互正交的匀强磁场和匀强电场的强度分别为和。平板上有可让粒子通过的狭缝和记录粒子位置的胶片,平板下方有磁感应强度为的匀强磁场。下列说法正确的是( )
A. 速度选择器中的磁场方向垂直纸面向里
B. 能通过狭缝的带电粒子的速率等于
C. 图中打在胶片上的粒子带负电
D. 粒子打在胶片上的位置越靠近狭缝,粒子的比荷越小
4. 某一个带有速度选择器的质谱仪原理如图所示,为粒子加速器,加速电压为;为速度选择器,磁场方向垂直纸面向里,磁感应强度为;的两板间距离为,电场方向向左或向右未知;为偏转分离器,磁感应强度为。今有一质量为、电荷量为的粒子不计重力,经加速后,该粒子恰能沿直线通过速度选择器,然后进入分离器做匀速圆周运动,下列分析正确的是( )
A. 该粒子不一定带正电
B. 区域中电场方向可能向右
C. 增大并相应减小,粒子才可能仍然沿直线通过
D. 增大并相应改变,使粒子仍然沿直线通过,在中的半径可能不变
5. 如图为一质谱仪的原理图,粒子源中有大量电量均为而质量不同的带电粒子,从进入间的加速电场,加速后进入电场强度和磁感应强度恒定不变的速度选择器间,能通过狭缝的粒子竖直向下垂直进入磁感应强度为的匀强磁场中,偏转后打到水平照相底片上形成谱线。若粒子在匀强磁场中的偏转距离为,不计粒子重力,则与的关系式为( )
A. B. C. D.
6. 图示装置叫质谱仪,最初是由阿斯顿设计的,是一种测量带电粒子的质量和分析同位素的重要工具。其工作原理如下:一个质量为、电荷量为的离子,从容器下方的小孔飘入电势差为的加速电场,其初速度几乎为零,然后经过沿着与磁场垂直的方向,进入磁感应强度为的匀强磁场中,最后打到底片上。不计离子重力。则( )
A. 离子进入磁场时的速率为
B. 离子在磁场中运动的轨迹半径为
C. 离子在磁场中运动的轨迹半径为
D. 若、是两种同位素的原子核,从底片上获知、在磁场中运动轨迹的直径之比是,则的质量之为
7. 如图为质谱仪的原理图,若同一束粒子沿极板、的轴线射入电磁场区域,由小孔射入右边的偏转磁场中,运动轨迹如图所示,不计粒子重力,下列相关说法中正确的是( )
A. 速度选择器的极板带负电
B. 该束带电粒子带正电
C. 在磁场中运动半径越大的粒子,速度越大
D. 在磁场中运动半径越大的粒子,比荷越大
8. 如图是质谱仪工作原理的示意图.带电粒子、经电压加速在点初速度为零后,进入磁感应强度为的匀强磁场做匀速圆周运动,最后分别打在感光板上的、处.图中半圆形的虚线分别表示带电粒子、所通过的路径,则( )
A. 若与有相同的质量,打在感光板上时,的速度比大
B. 若与有相同的质量,则的电荷量比的电荷量小
C. 若与有相同的电荷量,则的质量比的质量大
D. 若与有相同的电荷量,则的质量比的质量小
9. 如图所示,一个质量为,电荷量为的带正电的粒子,从静止开始经电压加速后,沿水平方向进入垂直于纸面向外的匀强磁场中,磁感应强度大小为,带电粒子经过半圆到点,设,不计粒子的重力,则能正确反映与之间关系的图象是( )
A. B. C. D.
10. 质谱仪可用于分析同位素,其结构如图所示一群质量数分别为和的正二价钙离子经电场加速后初速度忽略不计,接着进入匀强磁场中,最后打在底片上,实际加速电压通常不是恒定值,而是有一定范围,若加速电压取值范围是,两种离子打在底片上的区域恰好不重叠,不计离子的重力和相互作用,则的值约为( )
A. B. C. D.
二、计算题(本大题共2小题,共40.0分)
11. 一个质量为、电荷量为的粒子,从容器下方的小孔飘入电势差为的加速电场,其初速度几乎为零,然后经过沿着与磁场垂直的方向进入磁感应强度为的匀强磁场中,最后打在照相底片上。求:
粒子进入磁场时的速率。
粒子在磁场中运动的轨道半径。
如图所示为质谱仪的构造原理图,它是一种分离和检测不同同位素的重要工具。质子数相同而中子数不同的同一元素的不同核素互称为同位素。现让待测的不同带电粒子经加速电场后进入速度选择器,速度选择器的平行金属板之间有相互正交的匀强磁场和匀强电场图中未画出,磁感应强度为,电场强度为,金属板板,在平板上有可让粒子通过的狭缝,带电粒子经过速度选择器后,立即从点沿垂直平板且垂直于磁场方向的速度进入磁感应强度为、并以平板为边界的有界匀强磁场中,在磁场中偏转后打在记录它的照相底片上,底片厚度可忽略不计,且与平板重合。根据粒子打在底片上的位置,便可以对它的比荷电荷量与质量之比情况进行分析。在下面的讨论中,磁感应强度为的匀强磁场区域足够大,空气阻力、带电粒子所受的重力及它们之间的相互作用力均可忽略不计。
带电粒子通过狭缝时的速度大小;
不同的带电粒子经加速电场加速后可获得不同的速率,这些粒子进入速度选择器后,要想使通过狭缝的带电粒子速度大一些,应怎样调整速度选择器的电场强度和磁感应强度的大小;
若用这个质谱仪分别观测氢的两种同位素离子和,它们分别打在照相底片上相距为的两点;若用这个质谱仪相同条件下再分别观测碳的两种同位素离子和,它们分别打在照相底片上相距为的两点。请通过计算说明,与的大小关系;
若氢的两种同位素离子所带电荷量为的质量分别为和,且已知,它们同时从加速电场射出。试分析说明这两种粒子哪一种先到达照相底片,并求出它们到达照相底片上的时间差。
12.
答案和解析
1.【答案】
【解析】
【分析】
粒子在电场中加速,粒子在磁场中作圆周运动,洛伦兹力提供向心力,结合求得粒子在磁场中运动的时间表达式。
本题的关键是熟练周期和半径的表达式,并指导同位素的概念:质子数相同、中子数不同不同相同。
【解答】
设加速电场的电压为,磁场的磁感应强度为,粒子电荷量为、质量为,
在电场中加速过程有:
在磁场中偏转有:
据几何关系有
粒子运动的时间
以上四式联立得:,
所以,,故C正确,ABD错误。
故选C。
2.【答案】
【解析】略
3.【答案】
【解析】
【分析】
根据带电粒子在电场中的加速判断电荷的电性,粒子经过速度选择器时所受的电场力和洛伦兹力平衡,根据平衡求出粒子经过速度选择器的速度,通过带电粒子在磁场中的偏转,根据半径的大小判断粒子比荷的大小。
本题主要考查了质谱仪的结构和工作原理,解决本题的关键知道粒子在速度选择器中做匀速直线运动,在磁场中做匀速圆周运动。
【解答】
A、根据加速电场,可知粒子带正电,则粒子在速度选择器中受到的电场力向右,则洛伦兹力向左,由左手定则可判断磁场方向垂直纸面向外,故A错误;
B、能通过狭缝的带电粒子,经过速度选择器时做直线运动,则:,解得:,故B正确;
C、由图可知,粒子在磁场中运动向左偏转,根据左手定则判定,粒子带正电,故C错误;
D、粒子进入磁场后,据牛顿第二定律可得:,解得:,知粒子打在胶片上的位置越靠近狭缝,则越小,粒子的比荷越大,故D错误;
故选:。
4.【答案】
【解析】解:该粒子在中的磁场中向右偏转,根据左手定则可知,粒子一定带正电,故A错误;
B.粒子做区域做直线运动,则电场力等于洛伦兹力,洛伦兹力向右,则电场力向左,可知电场方向向左,故B错误;
C.增大则粒子进入区域的速度增加,若相应减小,则洛伦兹力与电场力仍可能相等,即粒子可能仍然沿直线通过,故C正确;
D.增大,粒子进入区域的速度增加,并相应改变,使粒子仍然沿直线通过,则粒子进入中的速度也增加,根据可得,可知在中的半径变大,故D错误。
故选:。
粒子经过速度选择器时,所受的电场力和洛伦兹力平衡,根据带电粒子在磁场中的偏转方向判断电荷的电性;根据平衡条件分析电场可能的方向;同时分析改变电压和磁场时变化时粒子的运动情况。
本题考查质谱仪模型,解决本题的关键知道粒子在速度选择器中做匀速直线运动,在磁场中做匀速圆周运动,明确洛伦兹力充当向心力。
5.【答案】
【解析】解:通过速度选择器的粒子满足,可得;进入偏转磁场后,由可得,,故A正确,BCD错误。
故选:。
带电粒子在速度选择器中受电场力和洛伦兹力平衡,做匀速直线运动,进入偏转电场后做匀速圆周运动,根据半径公式得出半径。
解决本题的关键知道粒子在速度选择器和偏转电场中的运动规律,掌握带电粒子在匀强磁场中运动的半径公式。
6.【答案】
【解析】
【分析】
带电粒子在电场中被加速,应用动能定理可以求出粒子的速度.粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的轨道半径.
、互为同位素,所以电荷量相等,由前面结论得出半径与质量之间的关系,然后由题目的条件即可求出.
【解答】
A、粒子在电场中加速,根据动能定理有,解得,故A错误;
、粒子进入磁场,洛伦兹力提供向心力,有,解得,故B错误,C正确;
D、若、是两种同位素的原子核,则他们的电量相同,质量不同,直径之比等于,则质量之比为,故D错误.
故选C.
7.【答案】
【解析】
【分析】
根据带电粒子在磁场中的偏转方向确定带电粒子的正负。根据在速度选择器中电场力和洛伦兹力平衡确定极板的带电情况。在磁场中,根据洛伦兹力提供向心力,求出粒子的轨道半径,即可知道轨迹半径与什么因素有关。
解决本题的关键会根据左手定则判断洛伦兹力的方向,以及知道在速度选择器中,电荷所受的电场力和洛伦兹力平衡,从速度选择器中沿直线飞出的粒子的速度相等。
【解答】
A.在偏转磁场中,磁场垂直向外,粒子向下偏,因此粒子带正电,而在平行金属板间,根据左手定则知,带电粒子所受的洛伦兹力方向竖直向上,则电场力的方向竖直向下,知电场强度的方向竖直向下,所以速度选择器的极板带正电,故A错误;
B.带电粒子在磁场中向下偏转,磁场的方向垂直纸面向外,根据左手定则知,该粒子带正电,故B正确;
进入磁场中的粒子速度是一定的,根据得,,知越大,比荷越小,故CD错误。
故选B。
8.【答案】
【解析】
【分析】
根据动能定理求出粒子出加速电场时的速度,通过洛伦兹力提供向心力,根据牛顿第二定律求出轨道半径的关系式,从而比较、的电量和质量关系。
本题考查了质谱仪的工作原理,要利用动能定理,洛伦兹力提供向心力等知识来解决问题。
【解答】
粒子在电场中加速,由动能定理得:解得:,
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,则,解得:,
根据图像可知粒子的半径小,粒子的半径大,若和质量相同,则的电量小,的速度小,若和的电量相等,因为的半径大,则的质量大,故D正确,ABC错误。
故选D。
9.【答案】
【解析】
【分析】
根据动能定理得到带电粒子加速获得的速度,带电粒子进入磁场中由洛伦兹力提供向心力做匀速圆周运动,由牛顿第二定律得到半径,,根据与的表达式选择图象。
本题主要考查带电粒子在匀强磁场中的运动规律及动能定理的应用。
【解答】
在加速电场中,由动能定理得 ,在磁场中,由 ,得:,则得:,、、都一定,则由数学知识得到,图象是开口向右的抛物线,故B正确,ACD错误。
故选B。
10.【答案】
【解析】
【分析】
两种离子打在底片上的区域恰好不重叠,则质量数为的离子的运动最大半径应等于质量数为的离子的最小半径,由此得解。
本题主要考查质谱仪的工作原理,熟悉其工作原理是解题的关键,有一定难度。
【解答】
正二价钙离子在电场中加速,由动能定理可得:,解得其进入磁场的速度为:,在磁场中离子由洛伦兹力提供向心力:,解得其圆周运动的半径为:。要使两种离子打在底片上的区域恰好不重叠,则需使质量数为的离子的运动最大半径应等于质量数为的离子的最小半径。质量数为的离子在磁场中运动的最大半径为:,质量数为的离子的最小半径为:,由可得:,解得,故A正确。
11.【答案】解:由动能定理得,
解得:
根据
得:
【解析】本题是动能定理和牛顿定律的综合题,解决本题的关键会灵活运用动能定理和牛顿定律。
12.【答案】解:带电粒子在速度选择器中做匀速直线运动,电场力与洛伦兹力平衡:
解得:
由知,要想使通过狭缝的带电粒子速度大一些,可减小或增大。
设的电荷量为,质量为,
在磁感应强度为的磁场中,洛伦兹力提供向心力:
由知
联立解得:
同理,在磁感应强度为的磁场中的轨迹半径
在磁感应强度为的磁场中的轨迹半径
在磁感应强度为的磁场中的轨迹半径
根据几何关系有:
故大于
氢的两种同位素离子同时从加速电场射出后,二者在速度选择器中速度相同,故运动时间相同,
在磁感应强度为的磁场中,质量为的离子的运动时间
又有
洛伦兹力提供向心力:
联立解得:
同理,质量为的离子的运动时间
因为
所以
所以质量为的离子先到达照相底片
它们到达照相底片上的时间差
答:带电粒子通过狭缝时的速度大小为;
不同的带电粒子经加速电场加速后可获得不同的速率,这些粒子进入速度选择器后,要想使通过狭缝的带电粒子速度大一些,可减小或增大;
若用这个质谱仪分别观测氢的两种同位素离子和,它们分别打在照相底片上相距为的两点;若用这个质谱仪相同条件下再分别观测碳的两种同位素离子和,它们分别打在照相底片上相距为的两点。与的大小关系为大于;
若氢的两种同位素离子所带电荷量为的质量分别为和,且已知,它们同时从加速电场射出。质量为的离子先到达照相底片,它们到达照相底片上的时间差为。
【解析】根据带电粒子在速度选择器中做匀速直线运动,电场力与洛伦兹力平衡分析;
根据的计算结果分析;
根据带电粒子在匀强磁场中洛伦兹力提供向心力求出半径,再结合几何关系分析;
根据带电粒子在匀强磁场中洛伦兹力提供向心力求出周期,再结合时间关系分析。
解答本题的关键是知道带电粒子在速度选择器中的速度均相同,在磁场中由洛伦兹力提供向心力。
第1页,共1页
