1.2 第2课时 直角三角形全等的判定 教案
文档属性
| 名称 | 1.2 第2课时 直角三角形全等的判定 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 14:37:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第2课时 直角三角形全等的判定
教学目标
【知识与技能】
1.已知斜边和直角边作直角三角形;
2.理解“斜边、直角边”定理,能够应用它证明两个三角形全等.
【过程与方法】
经历证明“斜边、直角边”定理的过程,并能掌握证明两个直角三角形全等的特殊方法——“斜边、直角边”定理.21世纪教育网版权所有
【情感、态度与价值观】
初步感受普遍性与特殊性之间的辩证关系,在探究性教学活动中增强学生的自主性和合作精神.
教学重难点
【教学重点】
“斜边、直角边”定理的理解与应用.
【教学难点】
“斜边、直角边”定理的证明过程的理解.
教学过程
一、问题导入
1.判断两个三角形全等的方法有哪几种
2.已知一条直角边和斜边,求作一个直角三角形.想一想,怎么画 同学们相互交流.
3.有两边及其中一边的对角对应相等的两个三角形全等吗 如果其中一个角是直角呢 请证明你的结论.
二、合作探究
探究点1 “斜边、直角边”定理
典例1 如图,在△ABC和△A'B'C'中,CD,C'D'分别是高,且AC=A'C',CD=C'D',∠ACB=∠A'C'B'.
求证:△ABC≌△A'B'C'.
[解析] ∵CD,C'D'分别是△ABC,△A'B'C'的高,∴∠ADC=∠A'D'C'=90°.
在Rt△ADC和Rt△A'D'C'中,AC=A'C',CD=C'D',
∴Rt△ADC≌Rt△A'D'C'(HL),
∴∠A=∠A'.
在△ABC和△A'B'C'中,∠A=∠A',AC=A'C',∠ACB=∠A'C'B',
∴△ABC≌△A'B'C'(ASA).
“斜边、直角边”(“HL”)定理,是判定两个直角三角形全等的独有方法,前面研究的判定两个三角形全等的判定方法“SAS,ASA,AAS,SSS”,对于判定两个直角三角形全等也是适用的,这样判定两个直角三角形全等一共有5种方法.21教育网
探究点2 “HL”定理的实际应用
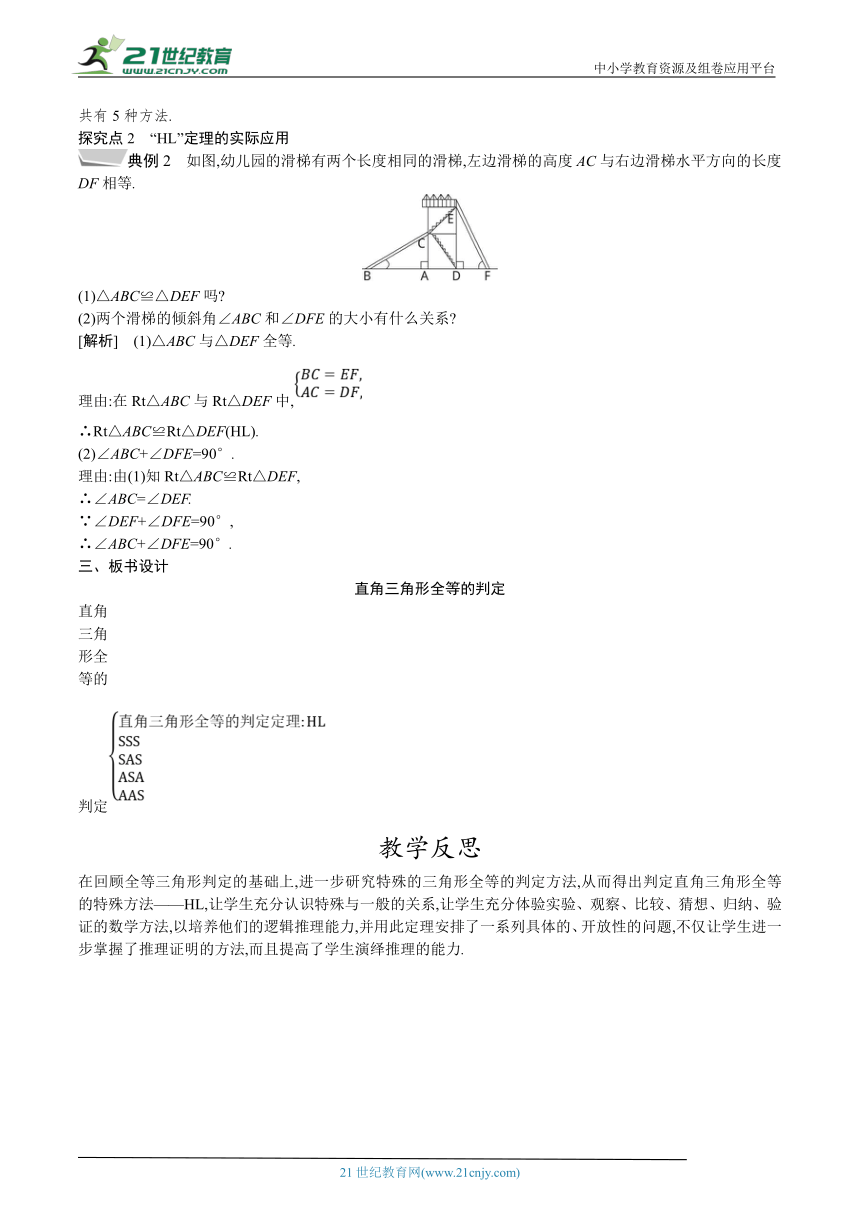
典例2 如图,幼儿园的滑梯有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.21cnjy.com
(1)△ABC≌△DEF吗
(2)两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系
[解析] (1)△ABC与△DEF全等.
理由:在Rt△ABC与Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).
(2)∠ABC+∠DFE=90°.
理由:由(1)知Rt△ABC≌Rt△DEF,
∴∠ABC=∠DEF.
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
三、板书设计
直角三角形全等的判定
直角
三角
形全
等的
判定
教学反思
在回顾全等三角形判定的基础上,进一步研究特殊的三角形全等的判定方法,从而得出判定直角三角形全等的特殊方法——HL,让学生充分认识特殊与一般的关系,让学生充分体验实验、观察、比较、猜想、归纳、验证的数学方法,以培养他们的逻辑推理能力,并用此定理安排了一系列具体的、开放性的问题,不仅让学生进一步掌握了推理证明的方法,而且提高了学生演绎推理的能力.21·cn·jy·com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第2课时 直角三角形全等的判定
教学目标
【知识与技能】
1.已知斜边和直角边作直角三角形;
2.理解“斜边、直角边”定理,能够应用它证明两个三角形全等.
【过程与方法】
经历证明“斜边、直角边”定理的过程,并能掌握证明两个直角三角形全等的特殊方法——“斜边、直角边”定理.21世纪教育网版权所有
【情感、态度与价值观】
初步感受普遍性与特殊性之间的辩证关系,在探究性教学活动中增强学生的自主性和合作精神.
教学重难点
【教学重点】
“斜边、直角边”定理的理解与应用.
【教学难点】
“斜边、直角边”定理的证明过程的理解.
教学过程
一、问题导入
1.判断两个三角形全等的方法有哪几种
2.已知一条直角边和斜边,求作一个直角三角形.想一想,怎么画 同学们相互交流.
3.有两边及其中一边的对角对应相等的两个三角形全等吗 如果其中一个角是直角呢 请证明你的结论.
二、合作探究
探究点1 “斜边、直角边”定理
典例1 如图,在△ABC和△A'B'C'中,CD,C'D'分别是高,且AC=A'C',CD=C'D',∠ACB=∠A'C'B'.
求证:△ABC≌△A'B'C'.
[解析] ∵CD,C'D'分别是△ABC,△A'B'C'的高,∴∠ADC=∠A'D'C'=90°.
在Rt△ADC和Rt△A'D'C'中,AC=A'C',CD=C'D',
∴Rt△ADC≌Rt△A'D'C'(HL),
∴∠A=∠A'.
在△ABC和△A'B'C'中,∠A=∠A',AC=A'C',∠ACB=∠A'C'B',
∴△ABC≌△A'B'C'(ASA).
“斜边、直角边”(“HL”)定理,是判定两个直角三角形全等的独有方法,前面研究的判定两个三角形全等的判定方法“SAS,ASA,AAS,SSS”,对于判定两个直角三角形全等也是适用的,这样判定两个直角三角形全等一共有5种方法.21教育网
探究点2 “HL”定理的实际应用
典例2 如图,幼儿园的滑梯有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.21cnjy.com
(1)△ABC≌△DEF吗
(2)两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系
[解析] (1)△ABC与△DEF全等.
理由:在Rt△ABC与Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).
(2)∠ABC+∠DFE=90°.
理由:由(1)知Rt△ABC≌Rt△DEF,
∴∠ABC=∠DEF.
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
三、板书设计
直角三角形全等的判定
直角
三角
形全
等的
判定
教学反思
在回顾全等三角形判定的基础上,进一步研究特殊的三角形全等的判定方法,从而得出判定直角三角形全等的特殊方法——HL,让学生充分认识特殊与一般的关系,让学生充分体验实验、观察、比较、猜想、归纳、验证的数学方法,以培养他们的逻辑推理能力,并用此定理安排了一系列具体的、开放性的问题,不仅让学生进一步掌握了推理证明的方法,而且提高了学生演绎推理的能力.21·cn·jy·com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
