4.5.1函数的零点与方程的解 课件(共16张PPT)
文档属性
| 名称 | 4.5.1函数的零点与方程的解 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-07 05:50:43 | ||
图片预览



文档简介
(共16张PPT)
函数零点与方程的解(1)
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
“ Work Report ”
授课对象:高一(12)班
授课人:邓芝
CONTENTS
Enter the relevant introduction here, as brief as possible.
Enter the relevant introduction here, as brief as possible.
Enter the relevant introduction here, as brief as possible.
Enter the relevant introduction here, as brief as possible.
2
1
学习目标
结合二次函数的图象,了解函数的零点与方程根的联系.
会求简单函数的零点、零点个数及零点所在的大致区间.
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
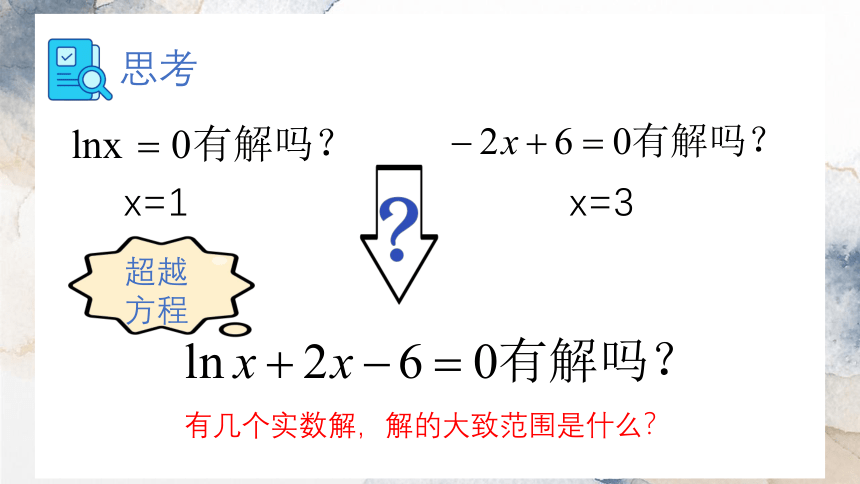
思考
x=1
x=3
超越方程
有几个实数解,解的大致范围是什么?
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
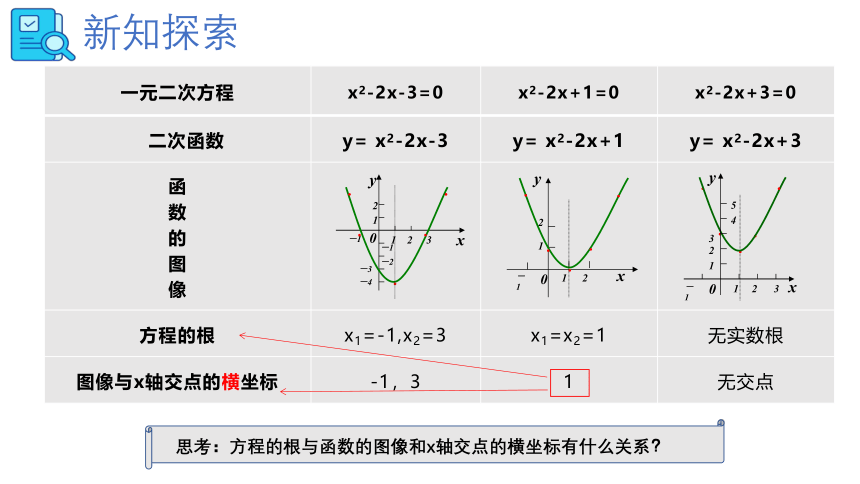
新知探索
一元二次方程 x2-2x-3=0 x2-2x+1=0 x2-2x+3=0
二次函数 y= x2-2x-3 y= x2-2x+1 y= x2-2x+3
函 数 的 图 像
方程的根 x1=-1,x2=3 x1=x2=1 无实数根
图像与x轴交点的横坐标 -1,3 1 无交点
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
y
x
0
-1
2
1
1
2
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
思考:方程的根与函数的图像和x轴交点的横坐标有什么关系?
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
概念生成
函数y=f(x)的零点
函数的零点:把使方程f(x)=0成立的实数x叫做函数 y=f(x)的零点
注意:零点不是点,是一个数值
方程f(x)=0的实数根
1.若y=f(x)表示函数y=f(x)的图像与x轴有公共点
2.若f(x)=g(x)-h(x),表示y=h(x)与y=g(x)的公共点
代数意义
几何意义
1.所有函数都存在零点吗?
2.什么条件下零点存在,存在一定唯一吗?
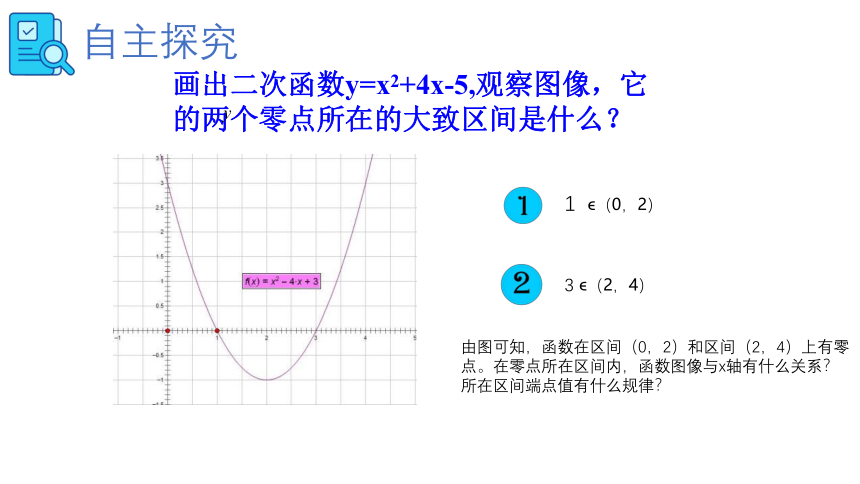
画出二次函数y=x2+4x-5,观察图像,它的两个零点所在的大致区间是什么?
x
y
自主探究
1 (0,2)
3 (2,4)
由图可知,函数在区间(0,2)和区间(2,4)上有零点。在零点所在区间内,函数图像与x轴有什么关系?所在区间端点值有什么规律?
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
情景探索
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
实验探索
小实验
函数y=f(x)在区间(a,b)内为连续函数,且满足f(a)f(b)<0
·(a,f(a))
·(a,f(a))
·(a,f(a))
·(b,f(b))
·(b,f(b))
·(b,f(b))
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
概念深化
函数零点存在性定理
如果函数y=f(x)在区间[a,b]上的图像是一条连续不断的曲线,且有f(a)f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点,即存在c (a,b),使得f(c)=0,这个c也就是方程f(x)=0的解
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
辨析比较
判断下列说法是否正确,如果不正确请举出反例
1.如果函数y=f(x)在区间[a,b]上的图像是一条连续不断的曲线,且在区间(a,b)内有零点,则可以推出来f(a)f(b)<0。
2.如果函数y=f(x)在区间[a,b]上满足f(a)f(b)<0,则f(x)在区间(a,b)上一定有零点。
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
新旧结合
在你学过的所有函数中,哪个函数f(x)在区间R内恰有0个、1个、2个,......,甚至无数个零点?
试举例说明.
例1.求方程lnx+2x-6=0实数解的个数,解的大致范围是什么
解:
设函数f(x)=lnx+2x-6,则 f(x)的定义域为(0,+∞)
列表,并作出f(x)的图象
x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972
f(2)<0, f(3)>0,
即 f(2) f(3)<0.
由函数零点存在定理,
f(x)在(2,3)内至少有一个零点.
又∵ f(x)=lnx+2x-6是增函数,
∴ f(x)是只有一个零点,
方程lnx+2x-6=0有1个实数解.
由表和图象得
f(x)=lnx+2x-6
典例练习
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
典例练习
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
典例练习
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
解:
典例练习
感谢の观看
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
“ Work Report ”
小卢子原创作品
适用用于工作总结计划 / 部门工作汇报 / 工作计划
函数零点与方程的解(1)
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
“ Work Report ”
授课对象:高一(12)班
授课人:邓芝
CONTENTS
Enter the relevant introduction here, as brief as possible.
Enter the relevant introduction here, as brief as possible.
Enter the relevant introduction here, as brief as possible.
Enter the relevant introduction here, as brief as possible.
2
1
学习目标
结合二次函数的图象,了解函数的零点与方程根的联系.
会求简单函数的零点、零点个数及零点所在的大致区间.
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
思考
x=1
x=3
超越方程
有几个实数解,解的大致范围是什么?
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
新知探索
一元二次方程 x2-2x-3=0 x2-2x+1=0 x2-2x+3=0
二次函数 y= x2-2x-3 y= x2-2x+1 y= x2-2x+3
函 数 的 图 像
方程的根 x1=-1,x2=3 x1=x2=1 无实数根
图像与x轴交点的横坐标 -1,3 1 无交点
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
y
x
0
-1
2
1
1
2
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
思考:方程的根与函数的图像和x轴交点的横坐标有什么关系?
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
概念生成
函数y=f(x)的零点
函数的零点:把使方程f(x)=0成立的实数x叫做函数 y=f(x)的零点
注意:零点不是点,是一个数值
方程f(x)=0的实数根
1.若y=f(x)表示函数y=f(x)的图像与x轴有公共点
2.若f(x)=g(x)-h(x),表示y=h(x)与y=g(x)的公共点
代数意义
几何意义
1.所有函数都存在零点吗?
2.什么条件下零点存在,存在一定唯一吗?
画出二次函数y=x2+4x-5,观察图像,它的两个零点所在的大致区间是什么?
x
y
自主探究
1 (0,2)
3 (2,4)
由图可知,函数在区间(0,2)和区间(2,4)上有零点。在零点所在区间内,函数图像与x轴有什么关系?所在区间端点值有什么规律?
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
情景探索
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
实验探索
小实验
函数y=f(x)在区间(a,b)内为连续函数,且满足f(a)f(b)<0
·(a,f(a))
·(a,f(a))
·(a,f(a))
·(b,f(b))
·(b,f(b))
·(b,f(b))
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
概念深化
函数零点存在性定理
如果函数y=f(x)在区间[a,b]上的图像是一条连续不断的曲线,且有f(a)f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点,即存在c (a,b),使得f(c)=0,这个c也就是方程f(x)=0的解
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
辨析比较
判断下列说法是否正确,如果不正确请举出反例
1.如果函数y=f(x)在区间[a,b]上的图像是一条连续不断的曲线,且在区间(a,b)内有零点,则可以推出来f(a)f(b)<0。
2.如果函数y=f(x)在区间[a,b]上满足f(a)f(b)<0,则f(x)在区间(a,b)上一定有零点。
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
新旧结合
在你学过的所有函数中,哪个函数f(x)在区间R内恰有0个、1个、2个,......,甚至无数个零点?
试举例说明.
例1.求方程lnx+2x-6=0实数解的个数,解的大致范围是什么
解:
设函数f(x)=lnx+2x-6,则 f(x)的定义域为(0,+∞)
列表,并作出f(x)的图象
x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972
f(2)<0, f(3)>0,
即 f(2) f(3)<0.
由函数零点存在定理,
f(x)在(2,3)内至少有一个零点.
又∵ f(x)=lnx+2x-6是增函数,
∴ f(x)是只有一个零点,
方程lnx+2x-6=0有1个实数解.
由表和图象得
f(x)=lnx+2x-6
典例练习
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
典例练习
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
典例练习
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
解:
典例练习
感谢の观看
Please enter the relevant text content here. Operation method: select all the text in this paragraph with the mouse, and enter the text directly to replace it. The text format will not change.
“ Work Report ”
小卢子原创作品
适用用于工作总结计划 / 部门工作汇报 / 工作计划
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
