4.4 课题学习 设计制作长方体形状的包装纸盒同步练习(含答案)
文档属性
| 名称 | 4.4 课题学习 设计制作长方体形状的包装纸盒同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 09:24:21 | ||
图片预览


文档简介
4.4 课题学习
设计制作长方体形状的包装纸盒
【基础强化】
知识点 设计制作长方体形状的包装纸盒
1.如图是一个正方体盒子的展开图,如果要把它粘成一个正方体,那么与点A重合的是( )
A.点B,I B.点C,E C.点B,E D.点C,H
2.如图是一个长方体纸盒,它的两个相邻面上各有一个阴影三角形,则该纸盒的展开图可能是( )
3.【卢龙县期末】如图是某正方体的展开图,在顶点处标有数字,当把它折成正方体时,与4重合的数字是( )
A.9和13 B.2和9 C.1和13 D.2和8
4.下列图形中,可以沿虚线折叠成长方体包装盒的有 .
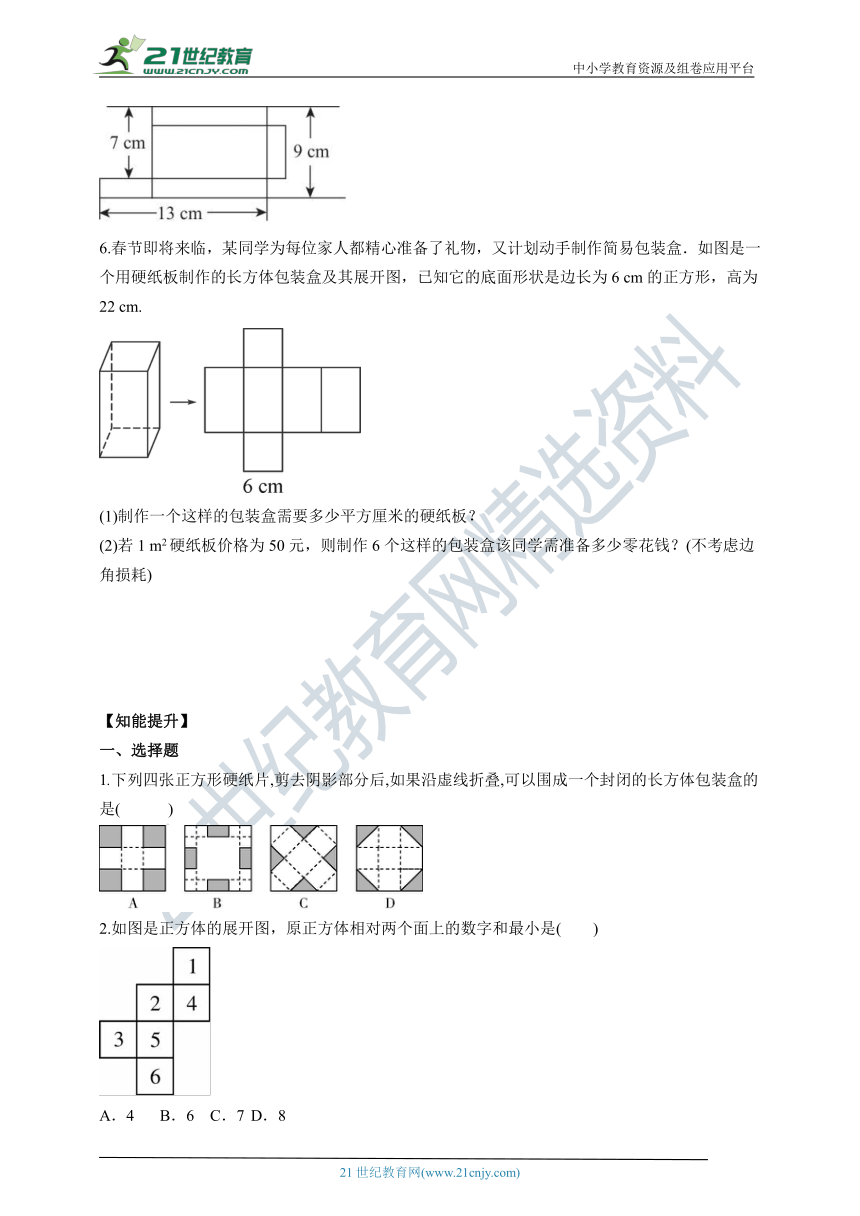
5.一个无盖长方体的包装盒展开图如图所示,则该长方体的体积为 cm3.
6.春节即将来临,某同学为每位家人都精心准备了礼物,又计划动手制作简易包装盒.如图是一个用硬纸板制作的长方体包装盒及其展开图,已知它的底面形状是边长为6 cm的正方形,高为22 cm.
(1)制作一个这样的包装盒需要多少平方厘米的硬纸板?
(2)若1 m2硬纸板价格为50元,则制作6个这样的包装盒该同学需准备多少零花钱?(不考虑边角损耗)
【知能提升】
一、选择题
1.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
2.如图是正方体的展开图,原正方体相对两个面上的数字和最小是( )
A.4 B.6 C.7 D.8
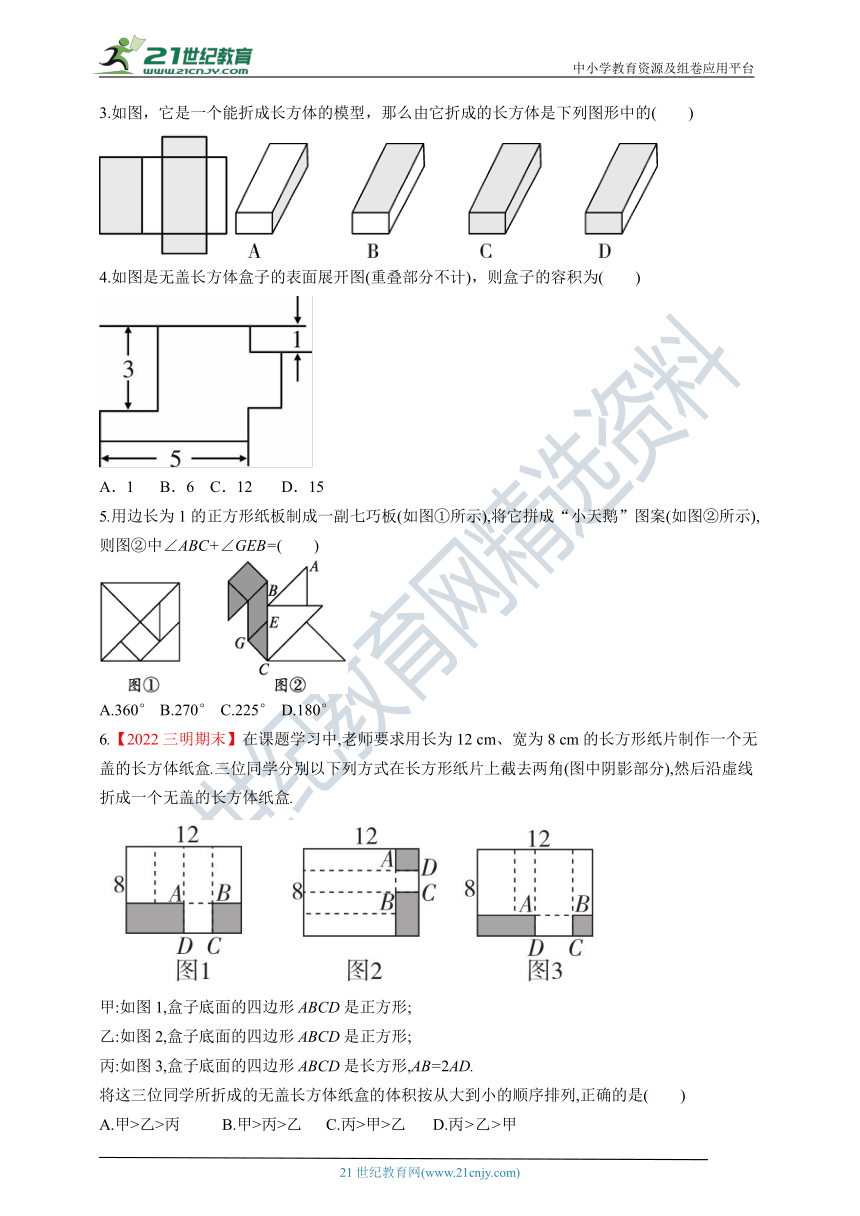
3.如图,它是一个能折成长方体的模型,那么由它折成的长方体是下列图形中的( )
4.如图是无盖长方体盒子的表面展开图(重叠部分不计),则盒子的容积为( )
A.1 B.6 C.12 D.15
5.用边长为1的正方形纸板制成一副七巧板(如图①所示),将它拼成“小天鹅”图案(如图②所示),则图②中∠ABC+∠GEB=( )
A.360° B.270° C.225° D.180°
6.【2022三明期末】在课题学习中,老师要求用长为12 cm、宽为8 cm的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体纸盒的体积按从大到小的顺序排列,正确的是( )
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
二、填空题
7.如图,纸上有10个小正方形(其中5个有阴影,5个无阴影),从图中5个无阴影的小正方形中选出一个,与5个有阴影的小正方形折出一个正方体的包装盒,不同的选法有 种.
8.图①是边长为30 cm的正方形纸板,裁掉阴影部分后将其折叠成长方体盒子如图②所示.已知该长方体的宽是高的2倍,则它的体积是 cm3.
三、解答题
9.小明将一个底面为正方形,高为n的无盖纸盒展开,如图1所示.
(1)请你计算图1所示的无盖纸盒的表面展开图的面积S1.
(2)将阴影部分剪拼成一个长方形,如图2所示,请你计算该长方形的面积S2.
(3)比较(1)(2)的结果,你得出什么结论
10.如图,在正方体两个相距最远的顶点处逗留着一只苍蝇和一只蜘蛛.蜘蛛可以从哪条最短的路径爬到苍蝇处 请说明理由.
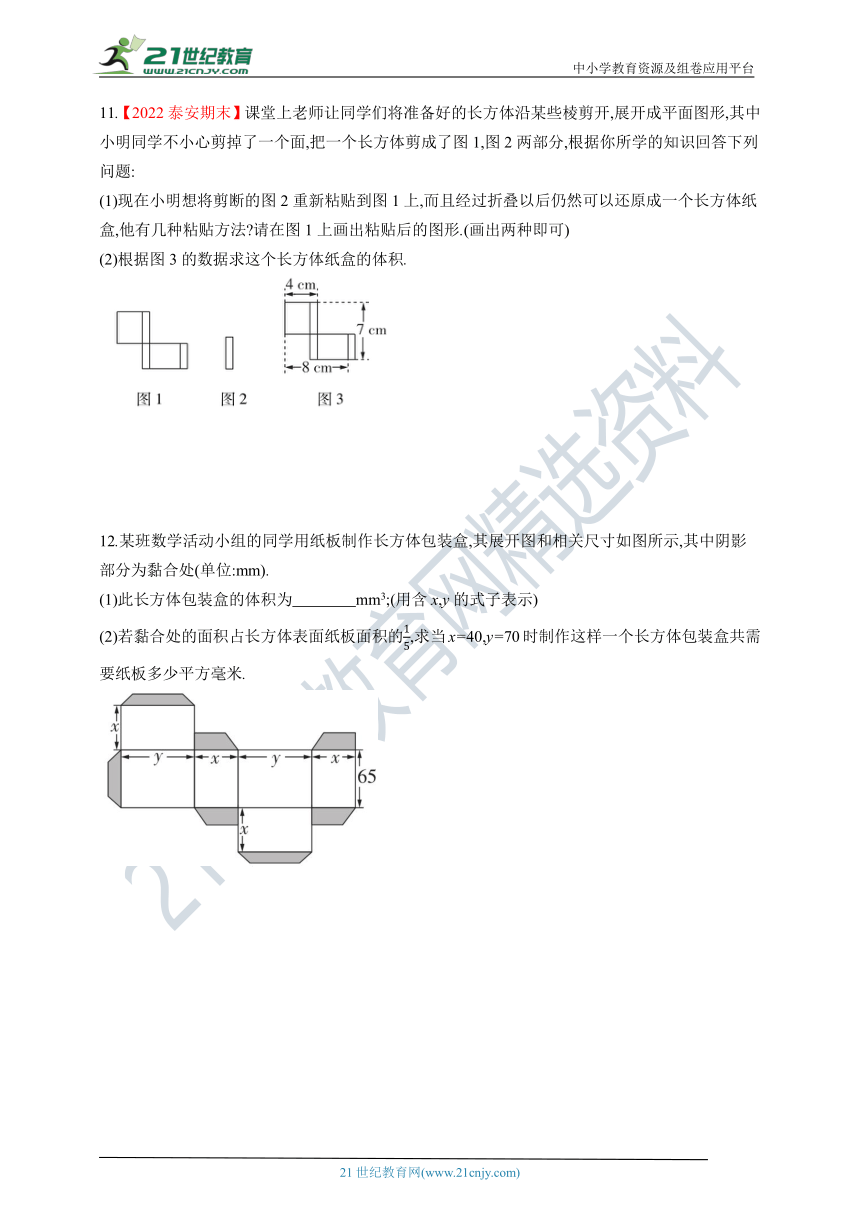
11.【2022泰安期末】课堂上老师让同学们将准备好的长方体沿某些棱剪开,展开成平面图形,其中小明同学不小心剪掉了一个面,把一个长方体剪成了图1,图2两部分,根据你所学的知识回答下列问题:
(1)现在小明想将剪断的图2重新粘贴到图1上,而且经过折叠以后仍然可以还原成一个长方体纸盒,他有几种粘贴方法 请在图1上画出粘贴后的图形.(画出两种即可)
(2)根据图3的数据求这个长方体纸盒的体积.
12.某班数学活动小组的同学用纸板制作长方体包装盒,其展开图和相关尺寸如图所示,其中阴影部分为黏合处(单位:mm).
(1)此长方体包装盒的体积为 mm3;(用含x,y的式子表示)
(2)若黏合处的面积占长方体表面纸板面积的,求当x=40,y=70时制作这样一个长方体包装盒共需要纸板多少平方毫米.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【基础强化】
知识点 设计制作长方体形状的包装纸盒
1.如图是一个正方体盒子的展开图,如果要把它粘成一个正方体,那么与点A重合的是( B )
A.点B,I B.点C,E C.点B,E D.点C,H
2.如图是一个长方体纸盒,它的两个相邻面上各有一个阴影三角形,则该纸盒的展开图可能是( A )
3.【卢龙县期末】如图是某正方体的展开图,在顶点处标有数字,当把它折成正方体时,与4重合的数字是( D )
A.9和13 B.2和9 C.1和13 D.2和8
4.下列图形中,可以沿虚线折叠成长方体包装盒的有 ①③ .
5.一个无盖长方体的包装盒展开图如图所示,则该长方体的体积为 80 cm3.
6.春节即将来临,某同学为每位家人都精心准备了礼物,又计划动手制作简易包装盒.如图是一个用硬纸板制作的长方体包装盒及其展开图,已知它的底面形状是边长为6 cm的正方形,高为22 cm.
(1)制作一个这样的包装盒需要多少平方厘米的硬纸板?
(2)若1 m2硬纸板价格为50元,则制作6个这样的包装盒该同学需准备多少零花钱?(不考虑边角损耗)
解:(1)6×6×2+6×4×22=600(cm2).
答:制作一个这样的包装盒需要600 cm2的硬纸板.
(2)600 cm2=0.06 m2,0.06×50×6=18(元),
答:制作6个这样的包装盒该同学需准备18元零花钱.
【知能提升】
一、选择题
1.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( C )
2.如图是正方体的展开图,原正方体相对两个面上的数字和最小是( B )
A.4 B.6 C.7 D.8
3.如图,它是一个能折成长方体的模型,那么由它折成的长方体是下列图形中的( D )
4.如图是无盖长方体盒子的表面展开图(重叠部分不计),则盒子的容积为( B )
A.1 B.6 C.12 D.15
5.用边长为1的正方形纸板制成一副七巧板(如图①所示),将它拼成“小天鹅”图案(如图②所示),则图②中∠ABC+∠GEB=( B )
A.360° B.270° C.225° D.180°
6.【2022三明期末】在课题学习中,老师要求用长为12 cm、宽为8 cm的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体纸盒的体积按从大到小的顺序排列,正确的是( C )
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
【解析】甲所折成的无盖长方体纸盒的体积为5×3×3=45(cm3),乙所折成的无盖长方体纸盒的体积为10×2×2=40(cm3),丙所折成的无盖长方体纸盒的体积为6×4×2=48(cm3),所以丙>甲>乙.
二、填空题
7.如图,纸上有10个小正方形(其中5个有阴影,5个无阴影),从图中5个无阴影的小正方形中选出一个,与5个有阴影的小正方形折出一个正方体的包装盒,不同的选法有 2 种.
8.图①是边长为30 cm的正方形纸板,裁掉阴影部分后将其折叠成长方体盒子如图②所示.已知该长方体的宽是高的2倍,则它的体积是 cm3.
【答案】1 000
【解析】设长方体的高为x cm,
则宽为(30-2x)cm.
根据题意,得(30-2x)=2x,
解得x=5.
故长方体的宽为10 cm,高为5 cm,长为30-5×2=20(cm),
则长方体的体积为5×10×20=1 000(cm3).
三、解答题
9.小明将一个底面为正方形,高为n的无盖纸盒展开,如图1所示.
(1)请你计算图1所示的无盖纸盒的表面展开图的面积S1.
(2)将阴影部分剪拼成一个长方形,如图2所示,请你计算该长方形的面积S2.
(3)比较(1)(2)的结果,你得出什么结论
解:(1)S1=(3m)2-4n2=9m2-4n2.
(2)长方形的长是3m+2n,宽是3m-2n,
所以S2=(3m+2n)(3m-2n).
(3)结论为9m2-4n2=(3m+2n)(3m-2n).
10.如图,在正方体两个相距最远的顶点处逗留着一只苍蝇和一只蜘蛛.蜘蛛可以从哪条最短的路径爬到苍蝇处 请说明理由.
解:在正方体的表面展开图上,根据两点之间,线段最短,可画出路线如图所示.(答案不唯一)
11.【2022泰安期末】课堂上老师让同学们将准备好的长方体沿某些棱剪开,展开成平面图形,其中小明同学不小心剪掉了一个面,把一个长方体剪成了图1,图2两部分,根据你所学的知识回答下列问题:
(1)现在小明想将剪断的图2重新粘贴到图1上,而且经过折叠以后仍然可以还原成一个长方体纸盒,他有几种粘贴方法 请在图1上画出粘贴后的图形.(画出两种即可)
(2)根据图3的数据求这个长方体纸盒的体积.
解:(1)根据展开图的特征,小明共有四种粘贴方法,四种情况如图所示.画出任意两种情况即可.
(2)8-4=4(cm),7-4=3(cm),4-3=1(cm),
所以长方体纸盒的体积为4×3×1=12(cm3).
12.某班数学活动小组的同学用纸板制作长方体包装盒,其展开图和相关尺寸如图所示,其中阴影部分为黏合处(单位:mm).
(1)此长方体包装盒的体积为 mm3;(用含x,y的式子表示)
(2)若黏合处的面积占长方体表面纸板面积的,求当x=40,y=70时制作这样一个长方体包装盒共需要纸板多少平方毫米.
解:(1)65xy
(2)由题意,得该长方体表面纸板的面积为2(xy+65y+65x)mm2,
又黏合处的面积占长方体表面纸板面积的,
所以制作这样一个长方体包装盒共需要纸板的面积为(1+)×2(xy+65y+65x)=(xy+65y+65x)(mm2),
当x=40,y=70时,(xy+65y+65x)=23 880,
所以制作这样一个长方体包装盒共需要纸板23 880 mm2.
设计制作长方体形状的包装纸盒
【基础强化】
知识点 设计制作长方体形状的包装纸盒
1.如图是一个正方体盒子的展开图,如果要把它粘成一个正方体,那么与点A重合的是( )
A.点B,I B.点C,E C.点B,E D.点C,H
2.如图是一个长方体纸盒,它的两个相邻面上各有一个阴影三角形,则该纸盒的展开图可能是( )
3.【卢龙县期末】如图是某正方体的展开图,在顶点处标有数字,当把它折成正方体时,与4重合的数字是( )
A.9和13 B.2和9 C.1和13 D.2和8
4.下列图形中,可以沿虚线折叠成长方体包装盒的有 .
5.一个无盖长方体的包装盒展开图如图所示,则该长方体的体积为 cm3.
6.春节即将来临,某同学为每位家人都精心准备了礼物,又计划动手制作简易包装盒.如图是一个用硬纸板制作的长方体包装盒及其展开图,已知它的底面形状是边长为6 cm的正方形,高为22 cm.
(1)制作一个这样的包装盒需要多少平方厘米的硬纸板?
(2)若1 m2硬纸板价格为50元,则制作6个这样的包装盒该同学需准备多少零花钱?(不考虑边角损耗)
【知能提升】
一、选择题
1.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
2.如图是正方体的展开图,原正方体相对两个面上的数字和最小是( )
A.4 B.6 C.7 D.8
3.如图,它是一个能折成长方体的模型,那么由它折成的长方体是下列图形中的( )
4.如图是无盖长方体盒子的表面展开图(重叠部分不计),则盒子的容积为( )
A.1 B.6 C.12 D.15
5.用边长为1的正方形纸板制成一副七巧板(如图①所示),将它拼成“小天鹅”图案(如图②所示),则图②中∠ABC+∠GEB=( )
A.360° B.270° C.225° D.180°
6.【2022三明期末】在课题学习中,老师要求用长为12 cm、宽为8 cm的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体纸盒的体积按从大到小的顺序排列,正确的是( )
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
二、填空题
7.如图,纸上有10个小正方形(其中5个有阴影,5个无阴影),从图中5个无阴影的小正方形中选出一个,与5个有阴影的小正方形折出一个正方体的包装盒,不同的选法有 种.
8.图①是边长为30 cm的正方形纸板,裁掉阴影部分后将其折叠成长方体盒子如图②所示.已知该长方体的宽是高的2倍,则它的体积是 cm3.
三、解答题
9.小明将一个底面为正方形,高为n的无盖纸盒展开,如图1所示.
(1)请你计算图1所示的无盖纸盒的表面展开图的面积S1.
(2)将阴影部分剪拼成一个长方形,如图2所示,请你计算该长方形的面积S2.
(3)比较(1)(2)的结果,你得出什么结论
10.如图,在正方体两个相距最远的顶点处逗留着一只苍蝇和一只蜘蛛.蜘蛛可以从哪条最短的路径爬到苍蝇处 请说明理由.
11.【2022泰安期末】课堂上老师让同学们将准备好的长方体沿某些棱剪开,展开成平面图形,其中小明同学不小心剪掉了一个面,把一个长方体剪成了图1,图2两部分,根据你所学的知识回答下列问题:
(1)现在小明想将剪断的图2重新粘贴到图1上,而且经过折叠以后仍然可以还原成一个长方体纸盒,他有几种粘贴方法 请在图1上画出粘贴后的图形.(画出两种即可)
(2)根据图3的数据求这个长方体纸盒的体积.
12.某班数学活动小组的同学用纸板制作长方体包装盒,其展开图和相关尺寸如图所示,其中阴影部分为黏合处(单位:mm).
(1)此长方体包装盒的体积为 mm3;(用含x,y的式子表示)
(2)若黏合处的面积占长方体表面纸板面积的,求当x=40,y=70时制作这样一个长方体包装盒共需要纸板多少平方毫米.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【基础强化】
知识点 设计制作长方体形状的包装纸盒
1.如图是一个正方体盒子的展开图,如果要把它粘成一个正方体,那么与点A重合的是( B )
A.点B,I B.点C,E C.点B,E D.点C,H
2.如图是一个长方体纸盒,它的两个相邻面上各有一个阴影三角形,则该纸盒的展开图可能是( A )
3.【卢龙县期末】如图是某正方体的展开图,在顶点处标有数字,当把它折成正方体时,与4重合的数字是( D )
A.9和13 B.2和9 C.1和13 D.2和8
4.下列图形中,可以沿虚线折叠成长方体包装盒的有 ①③ .
5.一个无盖长方体的包装盒展开图如图所示,则该长方体的体积为 80 cm3.
6.春节即将来临,某同学为每位家人都精心准备了礼物,又计划动手制作简易包装盒.如图是一个用硬纸板制作的长方体包装盒及其展开图,已知它的底面形状是边长为6 cm的正方形,高为22 cm.
(1)制作一个这样的包装盒需要多少平方厘米的硬纸板?
(2)若1 m2硬纸板价格为50元,则制作6个这样的包装盒该同学需准备多少零花钱?(不考虑边角损耗)
解:(1)6×6×2+6×4×22=600(cm2).
答:制作一个这样的包装盒需要600 cm2的硬纸板.
(2)600 cm2=0.06 m2,0.06×50×6=18(元),
答:制作6个这样的包装盒该同学需准备18元零花钱.
【知能提升】
一、选择题
1.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( C )
2.如图是正方体的展开图,原正方体相对两个面上的数字和最小是( B )
A.4 B.6 C.7 D.8
3.如图,它是一个能折成长方体的模型,那么由它折成的长方体是下列图形中的( D )
4.如图是无盖长方体盒子的表面展开图(重叠部分不计),则盒子的容积为( B )
A.1 B.6 C.12 D.15
5.用边长为1的正方形纸板制成一副七巧板(如图①所示),将它拼成“小天鹅”图案(如图②所示),则图②中∠ABC+∠GEB=( B )
A.360° B.270° C.225° D.180°
6.【2022三明期末】在课题学习中,老师要求用长为12 cm、宽为8 cm的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体纸盒的体积按从大到小的顺序排列,正确的是( C )
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
【解析】甲所折成的无盖长方体纸盒的体积为5×3×3=45(cm3),乙所折成的无盖长方体纸盒的体积为10×2×2=40(cm3),丙所折成的无盖长方体纸盒的体积为6×4×2=48(cm3),所以丙>甲>乙.
二、填空题
7.如图,纸上有10个小正方形(其中5个有阴影,5个无阴影),从图中5个无阴影的小正方形中选出一个,与5个有阴影的小正方形折出一个正方体的包装盒,不同的选法有 2 种.
8.图①是边长为30 cm的正方形纸板,裁掉阴影部分后将其折叠成长方体盒子如图②所示.已知该长方体的宽是高的2倍,则它的体积是 cm3.
【答案】1 000
【解析】设长方体的高为x cm,
则宽为(30-2x)cm.
根据题意,得(30-2x)=2x,
解得x=5.
故长方体的宽为10 cm,高为5 cm,长为30-5×2=20(cm),
则长方体的体积为5×10×20=1 000(cm3).
三、解答题
9.小明将一个底面为正方形,高为n的无盖纸盒展开,如图1所示.
(1)请你计算图1所示的无盖纸盒的表面展开图的面积S1.
(2)将阴影部分剪拼成一个长方形,如图2所示,请你计算该长方形的面积S2.
(3)比较(1)(2)的结果,你得出什么结论
解:(1)S1=(3m)2-4n2=9m2-4n2.
(2)长方形的长是3m+2n,宽是3m-2n,
所以S2=(3m+2n)(3m-2n).
(3)结论为9m2-4n2=(3m+2n)(3m-2n).
10.如图,在正方体两个相距最远的顶点处逗留着一只苍蝇和一只蜘蛛.蜘蛛可以从哪条最短的路径爬到苍蝇处 请说明理由.
解:在正方体的表面展开图上,根据两点之间,线段最短,可画出路线如图所示.(答案不唯一)
11.【2022泰安期末】课堂上老师让同学们将准备好的长方体沿某些棱剪开,展开成平面图形,其中小明同学不小心剪掉了一个面,把一个长方体剪成了图1,图2两部分,根据你所学的知识回答下列问题:
(1)现在小明想将剪断的图2重新粘贴到图1上,而且经过折叠以后仍然可以还原成一个长方体纸盒,他有几种粘贴方法 请在图1上画出粘贴后的图形.(画出两种即可)
(2)根据图3的数据求这个长方体纸盒的体积.
解:(1)根据展开图的特征,小明共有四种粘贴方法,四种情况如图所示.画出任意两种情况即可.
(2)8-4=4(cm),7-4=3(cm),4-3=1(cm),
所以长方体纸盒的体积为4×3×1=12(cm3).
12.某班数学活动小组的同学用纸板制作长方体包装盒,其展开图和相关尺寸如图所示,其中阴影部分为黏合处(单位:mm).
(1)此长方体包装盒的体积为 mm3;(用含x,y的式子表示)
(2)若黏合处的面积占长方体表面纸板面积的,求当x=40,y=70时制作这样一个长方体包装盒共需要纸板多少平方毫米.
解:(1)65xy
(2)由题意,得该长方体表面纸板的面积为2(xy+65y+65x)mm2,
又黏合处的面积占长方体表面纸板面积的,
所以制作这样一个长方体包装盒共需要纸板的面积为(1+)×2(xy+65y+65x)=(xy+65y+65x)(mm2),
当x=40,y=70时,(xy+65y+65x)=23 880,
所以制作这样一个长方体包装盒共需要纸板23 880 mm2.
