苏教版高中数学必修1《函数的概念和图象(第1课时)》教学课件1(共17张PPT)
文档属性
| 名称 | 苏教版高中数学必修1《函数的概念和图象(第1课时)》教学课件1(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 446.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-07 15:20:26 | ||
图片预览






文档简介
(共17张PPT)
2.1.1 函数的概念和图象
第1课时 函数的概念和定义域
[学习目标]
1.理解函数的概念。
2.了解构成函数的要素。
3.会求一些简单函数的定义域和函数值。
无意义
y=kx(k≠0)
y=ax+b(a≠0)
y=ax2+bx+c(a≠0)
[预习导引]
1.设A,B是两个 ,如果按照某种对应法则f,对于集合A中的 ,在集合B中都有 的元素y和它对应,那么这样的对应叫做从A到B的一个函数,通常记为 。
2.在函数y=f(x),x ∈ A中, 组成的集合A叫做函数y=f(x)的定义域, 组成的集合C={f(x)|x ∈ A}叫做函数y=f(x)的值域,且有C B。
非空数集
每一个元素x
唯一
y=f(x),x ∈ A
x的取值
y的取值
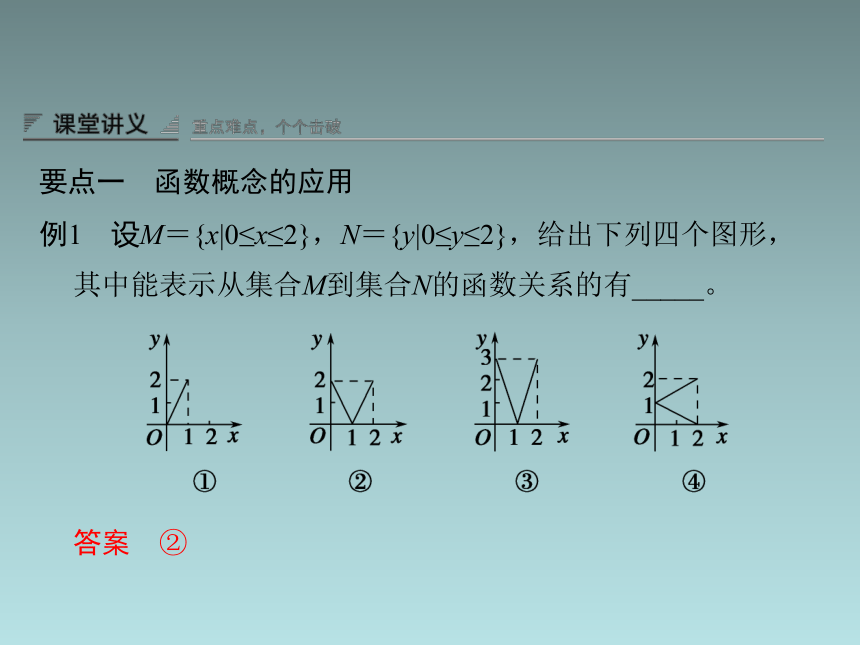
要点一 函数概念的应用
例1 设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示从集合M到集合N的函数关系的有_____。
答案 ②
解析
图号 正误 原因
① × x=2时,在N中无元素与之对应,不满足任意性。
② √ 同时满足任意性与唯一性。
③ × x=2时,对应元素y=3 N,不满足任意性。
④ × x=1时,在N中有两个元素与之对应,不满足唯一性。
规律方法 1.判断一个对应关系是否是函数关系的方法:(1)A,B必须都是非空数集;(2)A中任意一个数在B中必须有并且是唯一的实数和它对应。
注意:A中元素无剩余,B中元素允许有剩余。
2.函数的定义中“任意一个x”与“有唯一确定的y”说明函数中两变量x,y的对应关系是“一对一”或者是“多对一”而不能是“一对多”。
规律方法 1.当函数是由解析式给出时,求函数的定义域就是求使解析式有意义的自变量的取值集合,必须考虑下列各种情形:(1)负数不能开偶次方,所以偶次根号下的式子大于或等于零;(2)分式中分母不能为0;(3)零次幂的底数不为0;(4)如果f(x)由几部分构成,那么函数的定义域是使各部分都有意义的实数的集合;(5)如果函数有实际背景,那么除符合上述要求外,还要符合实际情况。
2.求函数的定义域,一般是转化为解不等式或不等式组的问题,注意定义域是一个集合,其结果必须用集合或区间来表示。
规律方法 求函数值时,首先要确定出函数的对应法则f的具体含义,然后将变量代入解析式计算,对于f[g(x)]型的求值,按“由内到外”的顺序进行,要注意f[g(x)]与g[f(x)]的区别。
2.1.1 函数的概念和图象
第1课时 函数的概念和定义域
[学习目标]
1.理解函数的概念。
2.了解构成函数的要素。
3.会求一些简单函数的定义域和函数值。
无意义
y=kx(k≠0)
y=ax+b(a≠0)
y=ax2+bx+c(a≠0)
[预习导引]
1.设A,B是两个 ,如果按照某种对应法则f,对于集合A中的 ,在集合B中都有 的元素y和它对应,那么这样的对应叫做从A到B的一个函数,通常记为 。
2.在函数y=f(x),x ∈ A中, 组成的集合A叫做函数y=f(x)的定义域, 组成的集合C={f(x)|x ∈ A}叫做函数y=f(x)的值域,且有C B。
非空数集
每一个元素x
唯一
y=f(x),x ∈ A
x的取值
y的取值
要点一 函数概念的应用
例1 设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示从集合M到集合N的函数关系的有_____。
答案 ②
解析
图号 正误 原因
① × x=2时,在N中无元素与之对应,不满足任意性。
② √ 同时满足任意性与唯一性。
③ × x=2时,对应元素y=3 N,不满足任意性。
④ × x=1时,在N中有两个元素与之对应,不满足唯一性。
规律方法 1.判断一个对应关系是否是函数关系的方法:(1)A,B必须都是非空数集;(2)A中任意一个数在B中必须有并且是唯一的实数和它对应。
注意:A中元素无剩余,B中元素允许有剩余。
2.函数的定义中“任意一个x”与“有唯一确定的y”说明函数中两变量x,y的对应关系是“一对一”或者是“多对一”而不能是“一对多”。
规律方法 1.当函数是由解析式给出时,求函数的定义域就是求使解析式有意义的自变量的取值集合,必须考虑下列各种情形:(1)负数不能开偶次方,所以偶次根号下的式子大于或等于零;(2)分式中分母不能为0;(3)零次幂的底数不为0;(4)如果f(x)由几部分构成,那么函数的定义域是使各部分都有意义的实数的集合;(5)如果函数有实际背景,那么除符合上述要求外,还要符合实际情况。
2.求函数的定义域,一般是转化为解不等式或不等式组的问题,注意定义域是一个集合,其结果必须用集合或区间来表示。
规律方法 求函数值时,首先要确定出函数的对应法则f的具体含义,然后将变量代入解析式计算,对于f[g(x)]型的求值,按“由内到外”的顺序进行,要注意f[g(x)]与g[f(x)]的区别。
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
