苏教版高中数学必修1《函数的概念和图象(第2课时)》教学课件1(共19张PPT)
文档属性
| 名称 | 苏教版高中数学必修1《函数的概念和图象(第2课时)》教学课件1(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 397.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-07 15:22:55 | ||
图片预览






文档简介
(共19张PPT)
2.1.1 函数的概念和图象
第2课时 函数的图象和值域
[学习目标]
1.会画一些简单函数的图象。
2.会求一些简单函数的值域。
向下
列表
描点
连线
直线
抛物线
向上
3.求函数的值域,不但要重视对应关系的作用,而且要特别注意定义域对值域的制约作用。要求函数的值域,首先应求其定义域。
要点一 作函数的图象
例1 作出下列函数的图象:
(1)y=1+x(x∈Z);
(2)y=x2-2x(x∈[0,3))。
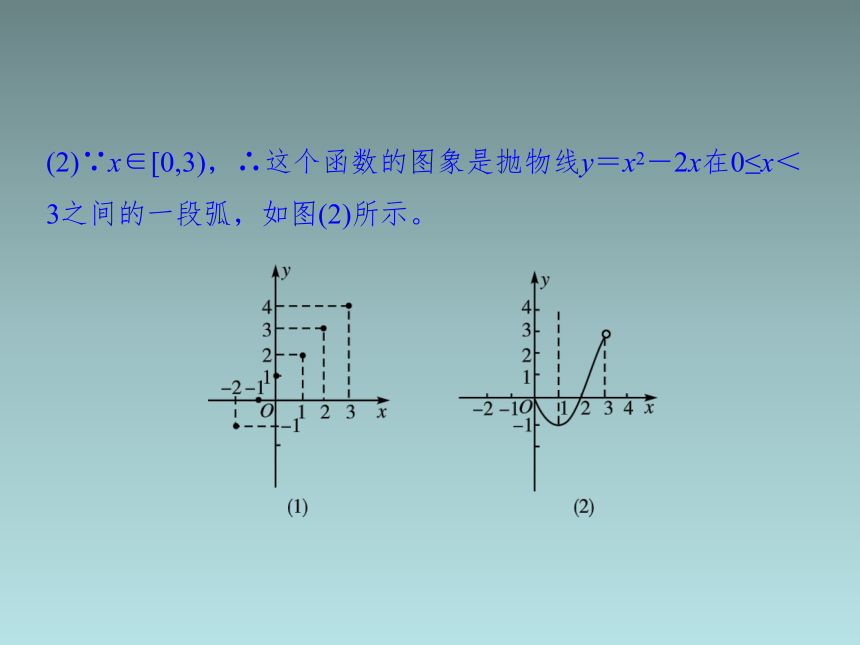
解 (1)这个函数的图象由一些点组成,这些点都在直线y=1+x上,如图(1)所示。
(2)∵x∈[0,3),∴这个函数的图象是抛物线y=x2-2x在0≤x<3之间的一段弧,如图(2)所示。
规律方法 (1)利用描点法作函数图象的基本步骤为:
(2)注意:函数的图象通常是一条连续的曲线或直线,但有时它也可以是一段或几段光滑曲线,也可以由一些孤立点或几段线段组成,还可以由折线或射线来构成,或者是点、线段、射线、折线和曲线组合而成,甚至可以是一些无规则的曲线。
跟踪演练1 画出下列函数的图象:
(1)y=1+x(x≤0);
(2)y=x2-2x(x>1或x<-1)。
解 如图.
要点二 利用函数图象求值域
例2 作出下列函数的图象并求其值域。
(1)y=1-x(x∈Z且|x|≤2);
(2)y=2x2-4x-3(0≤x<3)。
解 (1)因为x∈Z且|x|≤2,
∴x∈{-2,-1,0,1,2},
所以图象为一条直线上的孤立点(如图(1)),
由图象知,y∈{-1,0,1,2,3}。
(2)∵y=2(x-1)2-5,
∴当x=0时,y=-3;
当x=3时,y=3;
当x=1时,y=-5。
所画函数的图象如图。
因为x∈[0,3),故图象是一段抛物线(如图(2))。
由图象可知,y∈[-5,3)。
规律方法 利用函数的图象求值域,要找准函数的定义域,以防画错图象,影响求值域。
跟踪演练2 求函数y=-x2-2x+1分别在下列条件下的值域。
(1)x∈R;(2)x∈[-1,1];(3)x∈[-1,2]。
解 函数y=-x2-2x+1=-(x+1)2+2的图象如图所示。
(1)当x∈R时,观察图知y≤2,即值域为(-∞,2]。
(2)当x∈[-1,1]时,
观察图象知f(1)≤y≤f(-1)。
∵f(-1)=-(-1)2-2×(-1)+1=2,
f(1)=-1-2+1=-2,∴值域为[-2,2]。
(3)当x∈[-1,2]时,观察图象知f(2)≤y≤f(-1)。
∵f(-1)=2,f(2)=-7,
∴值域为[-7,2]。
要点三 函数图象的平移与变换
例3 分别在同一坐标系中作出下列两组函数的图象,并探究它们图象之间的关系?
(1)y=x,y=|x|,y=|x-1|;
(2)y=x2,y=(x-1)2,y=(x-1)2+1。
解 (1)在同一坐标系中分别用描点法作出
它们的图象,如图(1)。
首先作出y=x的图象,当作完y=|x|的图象
时,我们发现只要把y=x在x轴下方的图象
翻折到x轴上方,就能得到y=|x|的图象,如果再把y=|x|的图象向右平移一个单位,就得到y=|x-1|的图象。
(2)在同一坐标系中用描点法分别作出
它们的图象,如图(2)。
由图象可以看出,把y=x2的图象向右
平移一个单位得y=(x-1)2的图象,
把y=(x-1)2的图象向上平移一个单位
得到y=(x-1)2+1的图象。
规律方法 (1)函数图象的平移变换:
①左右平移:y=f(x)的图象向右(a>0)或向左(a<0)平移|a|个单位得到y=f(x-a)的图象。
②上下平移:y=f(x)的图象向上(a>0)或向下(a<0)平移|a|个单位得y=f(x)+a的图象。
(2)函数图象的对称变换:
①y=f(-x)的图象与y=f(x)的图象关于y轴对称;
②y=-f(x)的图象与y=f(x)的图象关于x轴对称;
③y=-f(-x)的图象与y=f(x)的图象关于原点对称;
④y=|f(x)|的图象是保留y=f(x)的图象中位于x轴及其上方的部分,将y=f(x)的图象中位于x轴下方的部分以x轴为对称轴翻折到x轴上方而得到;
⑤y=f(|x|)的图象是保留y=f(x)的图象中位于y轴及其右侧的部分,去掉位于y轴左侧的部分,再将右侧部分以y轴为对称轴翻折到左侧而得到。
2.1.1 函数的概念和图象
第2课时 函数的图象和值域
[学习目标]
1.会画一些简单函数的图象。
2.会求一些简单函数的值域。
向下
列表
描点
连线
直线
抛物线
向上
3.求函数的值域,不但要重视对应关系的作用,而且要特别注意定义域对值域的制约作用。要求函数的值域,首先应求其定义域。
要点一 作函数的图象
例1 作出下列函数的图象:
(1)y=1+x(x∈Z);
(2)y=x2-2x(x∈[0,3))。
解 (1)这个函数的图象由一些点组成,这些点都在直线y=1+x上,如图(1)所示。
(2)∵x∈[0,3),∴这个函数的图象是抛物线y=x2-2x在0≤x<3之间的一段弧,如图(2)所示。
规律方法 (1)利用描点法作函数图象的基本步骤为:
(2)注意:函数的图象通常是一条连续的曲线或直线,但有时它也可以是一段或几段光滑曲线,也可以由一些孤立点或几段线段组成,还可以由折线或射线来构成,或者是点、线段、射线、折线和曲线组合而成,甚至可以是一些无规则的曲线。
跟踪演练1 画出下列函数的图象:
(1)y=1+x(x≤0);
(2)y=x2-2x(x>1或x<-1)。
解 如图.
要点二 利用函数图象求值域
例2 作出下列函数的图象并求其值域。
(1)y=1-x(x∈Z且|x|≤2);
(2)y=2x2-4x-3(0≤x<3)。
解 (1)因为x∈Z且|x|≤2,
∴x∈{-2,-1,0,1,2},
所以图象为一条直线上的孤立点(如图(1)),
由图象知,y∈{-1,0,1,2,3}。
(2)∵y=2(x-1)2-5,
∴当x=0时,y=-3;
当x=3时,y=3;
当x=1时,y=-5。
所画函数的图象如图。
因为x∈[0,3),故图象是一段抛物线(如图(2))。
由图象可知,y∈[-5,3)。
规律方法 利用函数的图象求值域,要找准函数的定义域,以防画错图象,影响求值域。
跟踪演练2 求函数y=-x2-2x+1分别在下列条件下的值域。
(1)x∈R;(2)x∈[-1,1];(3)x∈[-1,2]。
解 函数y=-x2-2x+1=-(x+1)2+2的图象如图所示。
(1)当x∈R时,观察图知y≤2,即值域为(-∞,2]。
(2)当x∈[-1,1]时,
观察图象知f(1)≤y≤f(-1)。
∵f(-1)=-(-1)2-2×(-1)+1=2,
f(1)=-1-2+1=-2,∴值域为[-2,2]。
(3)当x∈[-1,2]时,观察图象知f(2)≤y≤f(-1)。
∵f(-1)=2,f(2)=-7,
∴值域为[-7,2]。
要点三 函数图象的平移与变换
例3 分别在同一坐标系中作出下列两组函数的图象,并探究它们图象之间的关系?
(1)y=x,y=|x|,y=|x-1|;
(2)y=x2,y=(x-1)2,y=(x-1)2+1。
解 (1)在同一坐标系中分别用描点法作出
它们的图象,如图(1)。
首先作出y=x的图象,当作完y=|x|的图象
时,我们发现只要把y=x在x轴下方的图象
翻折到x轴上方,就能得到y=|x|的图象,如果再把y=|x|的图象向右平移一个单位,就得到y=|x-1|的图象。
(2)在同一坐标系中用描点法分别作出
它们的图象,如图(2)。
由图象可以看出,把y=x2的图象向右
平移一个单位得y=(x-1)2的图象,
把y=(x-1)2的图象向上平移一个单位
得到y=(x-1)2+1的图象。
规律方法 (1)函数图象的平移变换:
①左右平移:y=f(x)的图象向右(a>0)或向左(a<0)平移|a|个单位得到y=f(x-a)的图象。
②上下平移:y=f(x)的图象向上(a>0)或向下(a<0)平移|a|个单位得y=f(x)+a的图象。
(2)函数图象的对称变换:
①y=f(-x)的图象与y=f(x)的图象关于y轴对称;
②y=-f(x)的图象与y=f(x)的图象关于x轴对称;
③y=-f(-x)的图象与y=f(x)的图象关于原点对称;
④y=|f(x)|的图象是保留y=f(x)的图象中位于x轴及其上方的部分,将y=f(x)的图象中位于x轴下方的部分以x轴为对称轴翻折到x轴上方而得到;
⑤y=f(|x|)的图象是保留y=f(x)的图象中位于y轴及其右侧的部分,去掉位于y轴左侧的部分,再将右侧部分以y轴为对称轴翻折到左侧而得到。
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
