角平分线的性质定理和逆定理

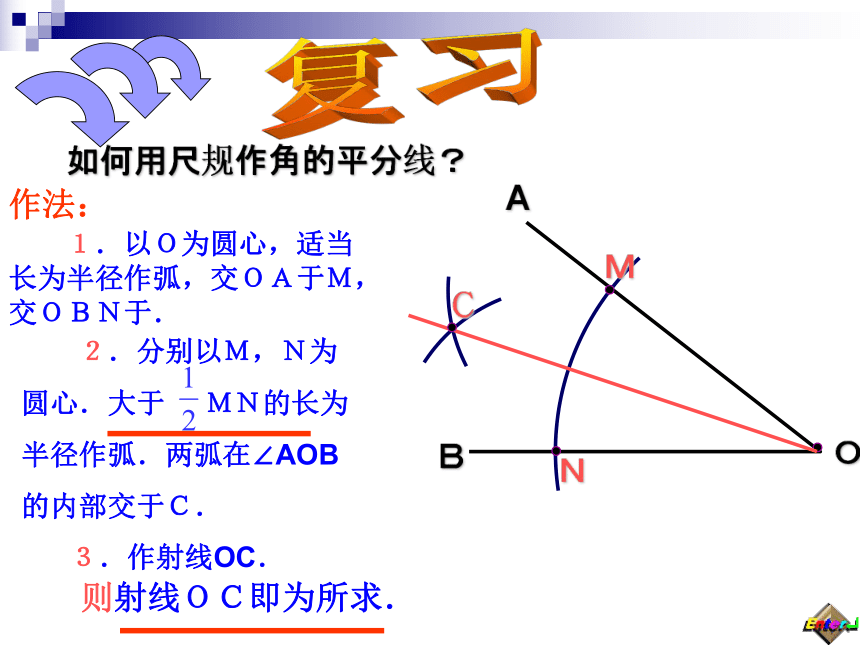
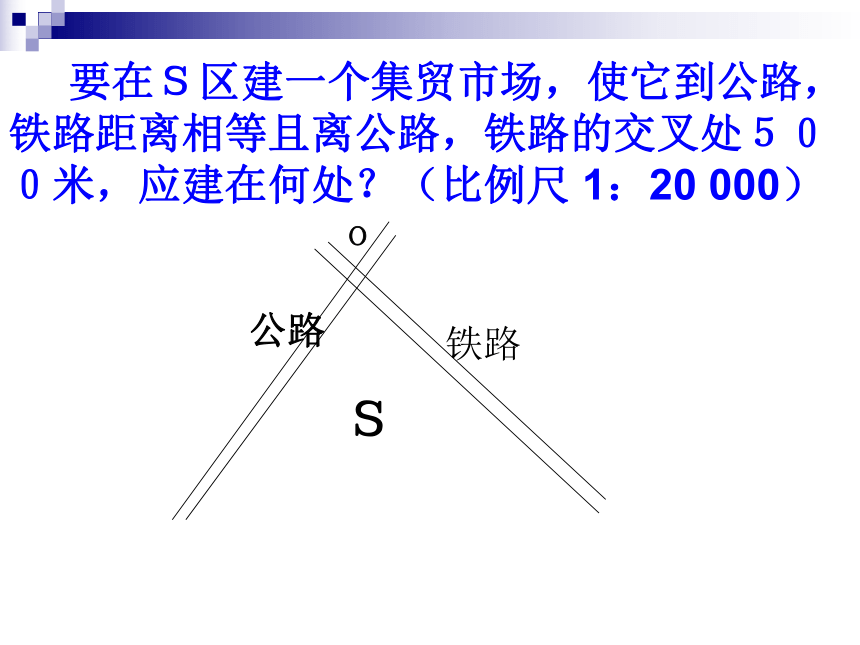
课件12张PPT。如何用尺规作角的平分线？AＢ作法：　　１．以Ｏ为圆心，适当长为半径作弧，交ＯＡ于Ｍ，交ＯＢＮ于．３．作射线OC．则射线ＯＣ即为所求．复习 要在Ｓ区建一个集贸市场，使它到公路，铁路距离相等且离公路，铁路的交叉处５００米，应建在何处？（比例尺 1：20 000）角平分线的性质
定理及其逆定理命题：角平分线上的点到角的两边的距离相等条件：一个点在一个角的平分线上结论：它到角的两边的距离相等 已知：OC是∠AOB的平分线，点P在 OC上，PD ⊥OA ，PE ⊥OB，
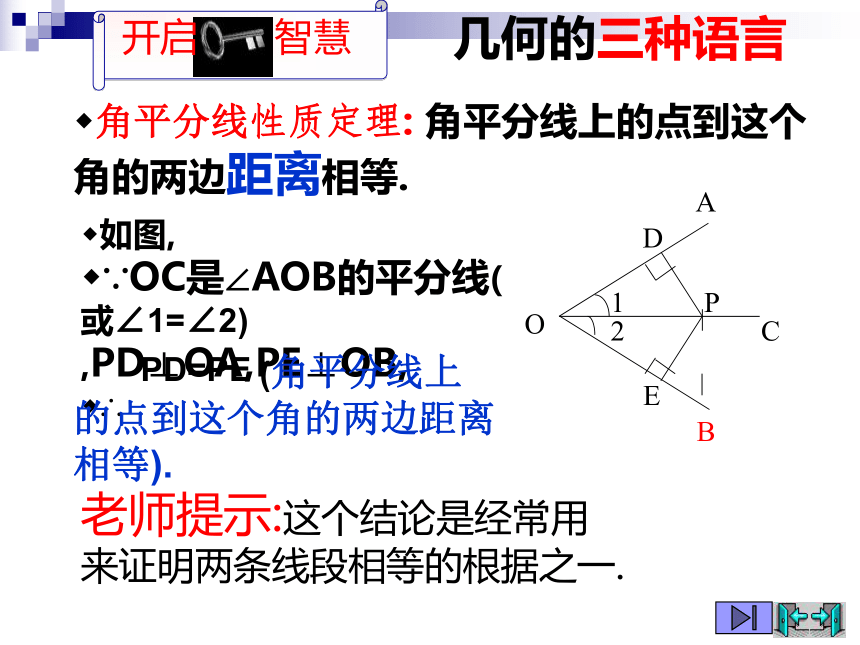
求证：PD=PE.C几何的三种语言角平分线性质定理: 角平分线上的点到这个角的两边距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.如图,
∵OC是∠AOB的平分线(或∠1=∠2) ,PD⊥OA,PE⊥OB,
∴ PD=PE (角平分线上的点到这个角的两边距离相等).
定理的逆命题该怎么说？到一个角的两边的距离相等的点，在这个角的平分线上。已知：如图，PD⊥OA，PE⊥OB，垂足分别
是D，E，PD=PE.
求证：点P在∠AOB的平分线上分析：
只要画射线OP，
证明OP平分
∠ AOB即可。判断下列推理是否正确（1）如图，∵AD平分∠BAC，PE⊥AB，PF⊥AC
∴PE = PF（角平分线上的点到这个角的
两边距离相等）（2）如图，∵ PE = PF
∴ AD平分∠BAC （到角两边距离相等的点
在这个角的平分线上）（3）如图，∵ 点P在∠BAC 的平分线上
∴ PE = PF（角平分线上的点到
这个角的两边距离相等）（对）（错）（错）判断下列推理是否正确（4）如图，∵ PE⊥AB，PF⊥AC ∴ AD平分∠BAC（到角两边距离相等
的点在这个角的平分线上）（错）（5）如图∵ PE⊥AB，PF⊥AC，PE = PF
∴点P在∠BAC 的平分线上（到角两边 距离相等的点在这个角的平分线上）（对） 已知：∠B = ∠Ｃ = 90°，DB = DC
　求证:∠ADB = ∠ADC
　　证明:∵∠B = ∠Ｃ = 90°（已知）
∴DB⊥AB,DC⊥AC（垂直的定义）
又∵DB = DC （已知）
∴点D在∠BAC的角平分线上
（到一个角的两边距离相等的点，
在这个角的角平分线上）
∴ ∠BAD = ∠CAD
∴ ∠ADB = ∠ADC(等角的余角相等)
角平分线的判定定理的应用1.如图,求作一点P,使PC=PD,并且点P到∠AOB的 两边的距离相等. 老师期望:
养成用数学解释生活的习惯. 2 .在△ABC中，∠B=∠C，点D为BC边的中点，DE⊥AB， DF⊥AC，垂足分别是E，F。求证：点D在∠A的平分线上。提示：先证△BDE≌△CDF(AAS)。 再由角平分线性质定理的逆定理即可得到结论。这节课你学到了什么小结：