人教版七上3.4实际应用与一元一次方程第4课时(球赛积分) 课件(共25张PPT)
文档属性
| 名称 | 人教版七上3.4实际应用与一元一次方程第4课时(球赛积分) 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 13:45:02 | ||
图片预览




文档简介
(共25张PPT)
3.4实际应用与一元一次方程
人教版七年级上册
教学目标
1.培养学生会阅读表格,并能从表格中提取关键信息.
2. 掌握解决“球赛积分”问题的一般思路.
3.培养学生的分析能力和解决实际问题的能力,使学生感受方程与实际生活的密切联系.
教学重点:探究解决实际问题的方法思路.
教学难点:将实际问题转化为一元一次方程的数学问题.
新知导入
各类球赛的比赛对我们都很大的吸引魅力,你能通过什么来判断一支球队在某联赛中的成绩的好坏(积分)?
新知讲解
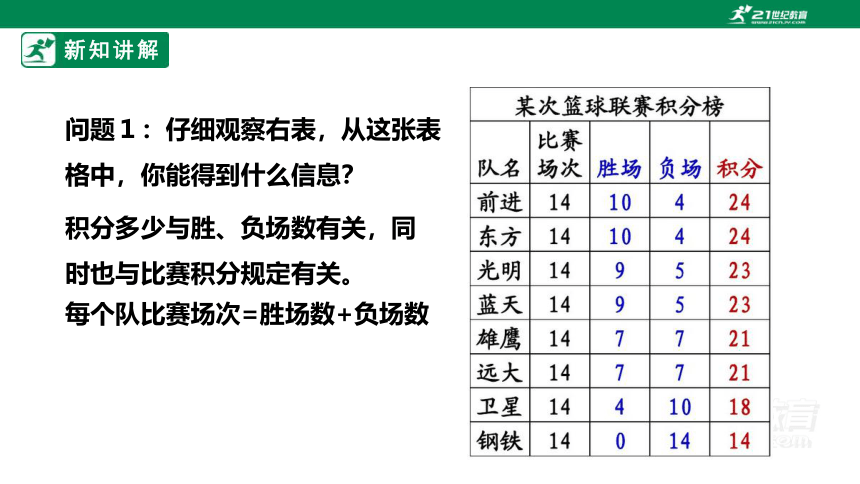
问题1:仔细观察右表,从这张表格中,你能得到什么信息?
每个队比赛场次=胜场数+负场数
积分多少与胜、负场数有关,同时也与比赛积分规定有关。
新知讲解
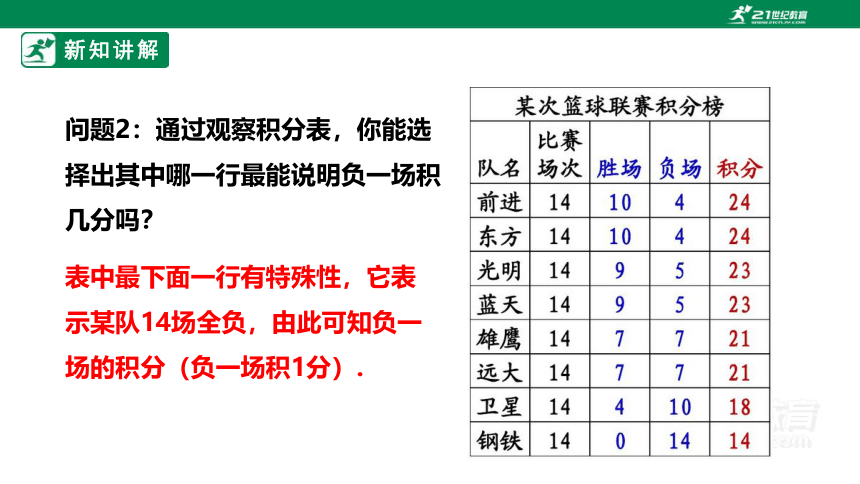
问题2:通过观察积分表,你能选择出其中哪一行最能说明负一场积几分吗?
表中最下面一行有特殊性,它表示某队14场全负,由此可知负一场的积分(负一场积1分).
新知讲解
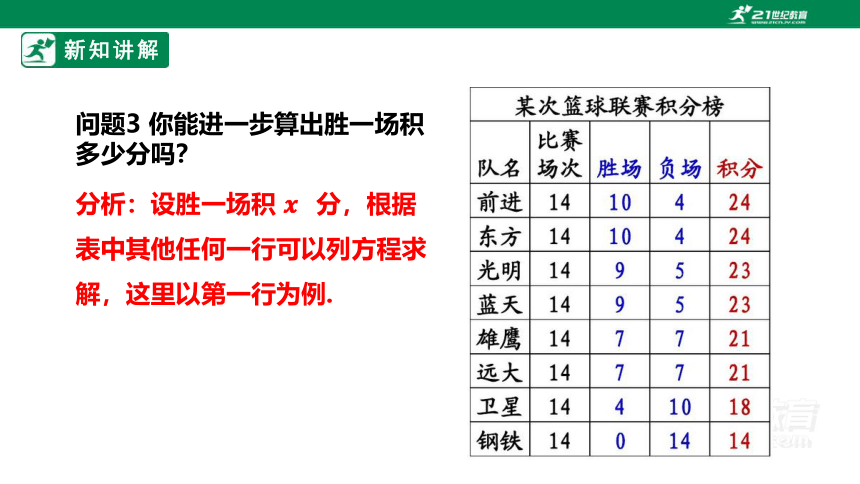
问题3 你能进一步算出胜一场积多少分吗?
分析:设胜一场积 分,根据表中其他任何一行可以列方程求解,这里以第一行为例.
新知讲解
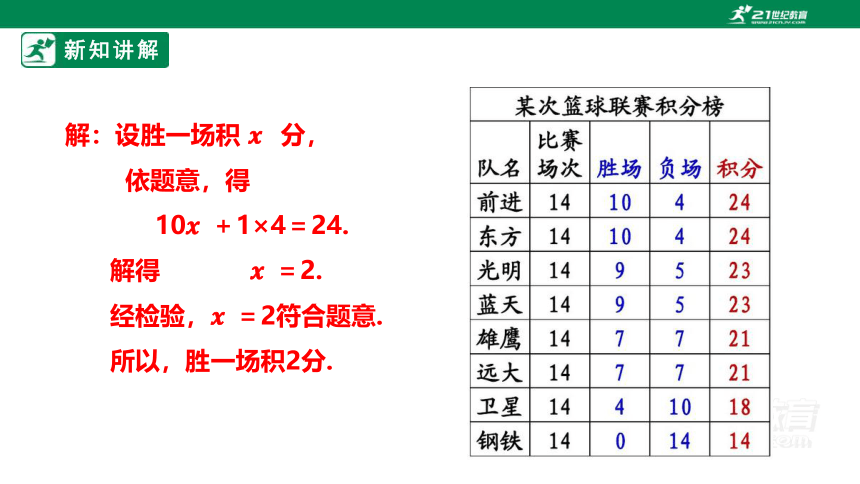
解:设胜一场积 分,
依题意,得
10 +1×4=24.
解得 =2.
经检验, =2符合题意.
所以,胜一场积2分.
新知讲解
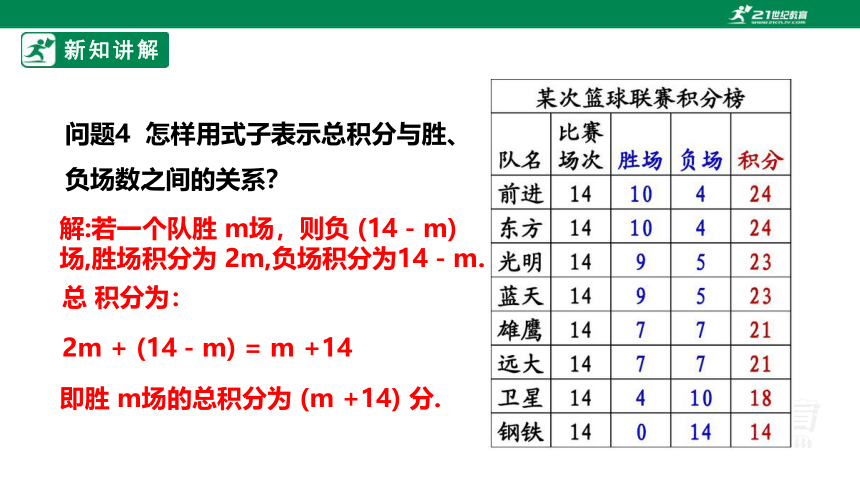
问题4 怎样用式子表示总积分与胜、负场数之间的关系?
解:若一个队胜 m场,则负 (14-m) 场,胜场积分为 2m,负场积分为14-m.
2m + (14-m) = m +14
总 积分为:
即胜 m场的总积分为 (m +14) 分.
新知讲解
问题5 某队胜场总积分能等于它负场总积分吗?
注意:上面的问题说明,用方程解决实际问题时不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义.
解:设一个队胜 场,则负 (14- ) 场,
依题意得 2 =14- .
解得
表示所胜的场数,必须是整数,所以不符合实际. 由此可以判定没有哪个队的胜场总积分等于负场总积分.
新知讲解
例:在一次有12个队参加的足球循环赛(每两队之间必须比赛一场)中,规定胜一场记3分,平一场记1分,负一场记0分.某队在这次循环赛中所胜场数比所负场数多2场,结果积18分.问该队战平几场?
分析:设该队负 场,用含 的式子表示出胜场数、平场数,再根据积分规则和等量关系“胜场得分+平场得分+负场得分=18”列方程求解.
新知讲解
解:设该队负 场,则胜( +2)场,
答:该队战平3场.
则平的场数为11- - ( +2)=-2 +9.
根据题意得
3( +2)+1×(-2 +9)+0× =0
解得 =5.
所以-2 +9=3
课堂练习
1. 一份数学试卷共25道选择题,每道题都给出了4个答案,其中只有一个符合题意选项,每道题选对得4分,不选或错选倒扣1分,已知小丽得了90分,设小丽做对了x道题,则下列所列方程正确的是( )
4x-(25-x)=90 B. x+4(25-x)=90
C. 4x+(25-x)=90 D. 4x-(25+x)=90
A
课堂练习
2. 在中学校园足球比赛中,记分规则为:胜一场得5分,平一场得2分,负一场得-1分,若猛士足球队共打了12场比赛,负4场,共得30分,则在这次比赛中猛士足球队胜了( )
3场
B. 4场
C. 5场
D. 6场
D
课堂练习
3. 某电视台组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了5个参赛者的得分情况
下列说法有误的是( )
A. 答对一题得5分,答错一题扣1分 B. 某参赛选手得了80分
C. 某参赛选手得了76分 D. 某参赛选手得分可能为负数
B
课堂练习
4. 某次篮球联赛积分表:
有以下判断:
①负一场积1分;
②胜一场积2分;
③如果一个队胜 m 场,则该队的总积分为 (m+12) 分;
④不可能有一个球队的胜场总积分等于它的负场总积分.
以上说法正确的个数是( )
A. 1 B. 2 C. 3 D. 4
C
课堂练习
5. 某球队参加比赛,开局11场保持不败,积23分,按比赛规则,胜一场得3分,平一场得1分,则该队获胜的场数为( )
A. 4 B. 5 C. 6 D. 7
6. 某校举办班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.如果七年级(1)班在8场比赛中共得13分,那么该班获胜的场数是( )
A. 4 B. 5 C. 6 D. 7
C
B
课堂练习
7. 某企业对应聘人员进行逻辑思维考试,试题由50道选择题组成,评分标准规定:每道题的答案选对得3分,不选得0分,选错倒扣1分.已知某人有5道题未做,得了103分,则这个人选错了几道题?
解:设这个人选错了x道题,根据题意得
3(50-x-5)-x=103
解得 x=8 ,
答:这个人选错了8道题.
课堂练习
8. 在一次有12个队参加的足球循环赛中(每两队之间比赛一场),规定胜一场记3分,平一场记1分,负一场记0分.某队在这次循环赛中所胜场数比所负场数多2场,结果共积19分.问:该队在这次循环赛中战平了几场?
课堂练习
解:设该队负了x场,则胜(x+2)场,
平局的场数为[11-x-(x+2)]场.
根据题意,得
3(x+2)+1×[11-x-(x+2)]=19,
解得x=4,
∴11-x-(x+2)=1.
答:该队在这次循环赛中战平了1场.
9. 为促进全民健身运动,某市组织了一次足球比赛,下表记录比赛过程中部分代表队的积分情况
(1)本次比赛中,胜一场积________分
(2)若E代表队完成10场比赛后,只输了一场,积分是23分,请求出E代表队胜出的场数
代表队 场次(场) 胜(场) 平(场) 负(场) 积分(场)
A 6 5 1 0 16
B 6 6 0 0 18
C 6 3 1 1 11
D 6 3 2 2 10
课堂练习
课堂练习
解:(1)由表格知:B代表队胜6场积18分,
∴胜一场的积分=18÷6=3分,
(2)解:设E代表队胜出x场,则平了(10﹣x﹣1)场,输了1场
由(1)知,胜一场积分为3分,则平一场积分为:16﹣3×5=1(分),
负一场积分为:11﹣3×3+1×2=0(分)
由题得 3x+1×(10﹣x﹣1)+1×0=23
解得x=7
答:E代表队胜出7场。
课堂总结
1.球赛积分中的等量关系是∶胜场的积分+负场的积分=总积分
2.方程解决实际问题时,不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义。
作业布置
第107页习题3.4
第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4实际应用与一元一次方程
人教版七年级上册
教学目标
1.培养学生会阅读表格,并能从表格中提取关键信息.
2. 掌握解决“球赛积分”问题的一般思路.
3.培养学生的分析能力和解决实际问题的能力,使学生感受方程与实际生活的密切联系.
教学重点:探究解决实际问题的方法思路.
教学难点:将实际问题转化为一元一次方程的数学问题.
新知导入
各类球赛的比赛对我们都很大的吸引魅力,你能通过什么来判断一支球队在某联赛中的成绩的好坏(积分)?
新知讲解
问题1:仔细观察右表,从这张表格中,你能得到什么信息?
每个队比赛场次=胜场数+负场数
积分多少与胜、负场数有关,同时也与比赛积分规定有关。
新知讲解
问题2:通过观察积分表,你能选择出其中哪一行最能说明负一场积几分吗?
表中最下面一行有特殊性,它表示某队14场全负,由此可知负一场的积分(负一场积1分).
新知讲解
问题3 你能进一步算出胜一场积多少分吗?
分析:设胜一场积 分,根据表中其他任何一行可以列方程求解,这里以第一行为例.
新知讲解
解:设胜一场积 分,
依题意,得
10 +1×4=24.
解得 =2.
经检验, =2符合题意.
所以,胜一场积2分.
新知讲解
问题4 怎样用式子表示总积分与胜、负场数之间的关系?
解:若一个队胜 m场,则负 (14-m) 场,胜场积分为 2m,负场积分为14-m.
2m + (14-m) = m +14
总 积分为:
即胜 m场的总积分为 (m +14) 分.
新知讲解
问题5 某队胜场总积分能等于它负场总积分吗?
注意:上面的问题说明,用方程解决实际问题时不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义.
解:设一个队胜 场,则负 (14- ) 场,
依题意得 2 =14- .
解得
表示所胜的场数,必须是整数,所以不符合实际. 由此可以判定没有哪个队的胜场总积分等于负场总积分.
新知讲解
例:在一次有12个队参加的足球循环赛(每两队之间必须比赛一场)中,规定胜一场记3分,平一场记1分,负一场记0分.某队在这次循环赛中所胜场数比所负场数多2场,结果积18分.问该队战平几场?
分析:设该队负 场,用含 的式子表示出胜场数、平场数,再根据积分规则和等量关系“胜场得分+平场得分+负场得分=18”列方程求解.
新知讲解
解:设该队负 场,则胜( +2)场,
答:该队战平3场.
则平的场数为11- - ( +2)=-2 +9.
根据题意得
3( +2)+1×(-2 +9)+0× =0
解得 =5.
所以-2 +9=3
课堂练习
1. 一份数学试卷共25道选择题,每道题都给出了4个答案,其中只有一个符合题意选项,每道题选对得4分,不选或错选倒扣1分,已知小丽得了90分,设小丽做对了x道题,则下列所列方程正确的是( )
4x-(25-x)=90 B. x+4(25-x)=90
C. 4x+(25-x)=90 D. 4x-(25+x)=90
A
课堂练习
2. 在中学校园足球比赛中,记分规则为:胜一场得5分,平一场得2分,负一场得-1分,若猛士足球队共打了12场比赛,负4场,共得30分,则在这次比赛中猛士足球队胜了( )
3场
B. 4场
C. 5场
D. 6场
D
课堂练习
3. 某电视台组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了5个参赛者的得分情况
下列说法有误的是( )
A. 答对一题得5分,答错一题扣1分 B. 某参赛选手得了80分
C. 某参赛选手得了76分 D. 某参赛选手得分可能为负数
B
课堂练习
4. 某次篮球联赛积分表:
有以下判断:
①负一场积1分;
②胜一场积2分;
③如果一个队胜 m 场,则该队的总积分为 (m+12) 分;
④不可能有一个球队的胜场总积分等于它的负场总积分.
以上说法正确的个数是( )
A. 1 B. 2 C. 3 D. 4
C
课堂练习
5. 某球队参加比赛,开局11场保持不败,积23分,按比赛规则,胜一场得3分,平一场得1分,则该队获胜的场数为( )
A. 4 B. 5 C. 6 D. 7
6. 某校举办班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.如果七年级(1)班在8场比赛中共得13分,那么该班获胜的场数是( )
A. 4 B. 5 C. 6 D. 7
C
B
课堂练习
7. 某企业对应聘人员进行逻辑思维考试,试题由50道选择题组成,评分标准规定:每道题的答案选对得3分,不选得0分,选错倒扣1分.已知某人有5道题未做,得了103分,则这个人选错了几道题?
解:设这个人选错了x道题,根据题意得
3(50-x-5)-x=103
解得 x=8 ,
答:这个人选错了8道题.
课堂练习
8. 在一次有12个队参加的足球循环赛中(每两队之间比赛一场),规定胜一场记3分,平一场记1分,负一场记0分.某队在这次循环赛中所胜场数比所负场数多2场,结果共积19分.问:该队在这次循环赛中战平了几场?
课堂练习
解:设该队负了x场,则胜(x+2)场,
平局的场数为[11-x-(x+2)]场.
根据题意,得
3(x+2)+1×[11-x-(x+2)]=19,
解得x=4,
∴11-x-(x+2)=1.
答:该队在这次循环赛中战平了1场.
9. 为促进全民健身运动,某市组织了一次足球比赛,下表记录比赛过程中部分代表队的积分情况
(1)本次比赛中,胜一场积________分
(2)若E代表队完成10场比赛后,只输了一场,积分是23分,请求出E代表队胜出的场数
代表队 场次(场) 胜(场) 平(场) 负(场) 积分(场)
A 6 5 1 0 16
B 6 6 0 0 18
C 6 3 1 1 11
D 6 3 2 2 10
课堂练习
课堂练习
解:(1)由表格知:B代表队胜6场积18分,
∴胜一场的积分=18÷6=3分,
(2)解:设E代表队胜出x场,则平了(10﹣x﹣1)场,输了1场
由(1)知,胜一场积分为3分,则平一场积分为:16﹣3×5=1(分),
负一场积分为:11﹣3×3+1×2=0(分)
由题得 3x+1×(10﹣x﹣1)+1×0=23
解得x=7
答:E代表队胜出7场。
课堂总结
1.球赛积分中的等量关系是∶胜场的积分+负场的积分=总积分
2.方程解决实际问题时,不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义。
作业布置
第107页习题3.4
第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
