人教版七上3.4实际应用与一元一次方程第5课时(方案选择问题) 课件(共28张PPT)
文档属性
| 名称 | 人教版七上3.4实际应用与一元一次方程第5课时(方案选择问题) 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 13:47:05 | ||
图片预览






文档简介
(共28张PPT)
3.4实际应用与一元一次方程
人教版七年级上册
教学目标
1.经历在消费过程中选择哪种消费方案的过程,掌握一些特殊的解决这类问题的方法.
2. 培养学生的分析能力和解决实际问题的能力,体会合作学习在解决问题过程中的重要意义.
3. 感受所学知识与现实生活的联系,从中获得价值体验;让学生在解决问题的过程中获得成功体验,增强学生学好数学的信心.
教学重点∶掌握解决这类问题的基本方法.
教学难点:是会运用一元一次方程解决问题.
新知导入
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
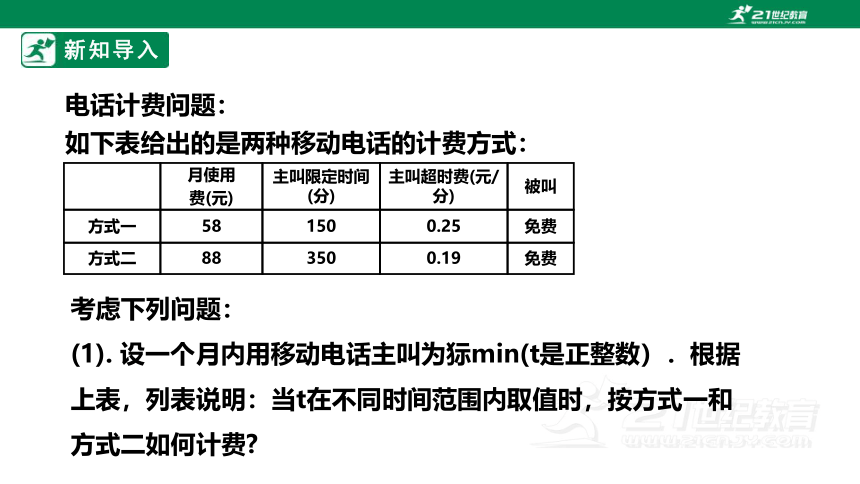
如下表给出的是两种移动电话的计费方式:
考虑下列问题:
(1). 设一个月内用移动电话主叫为狋min(t是正整数).根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费
电话计费问题:
新知讲解
分析:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
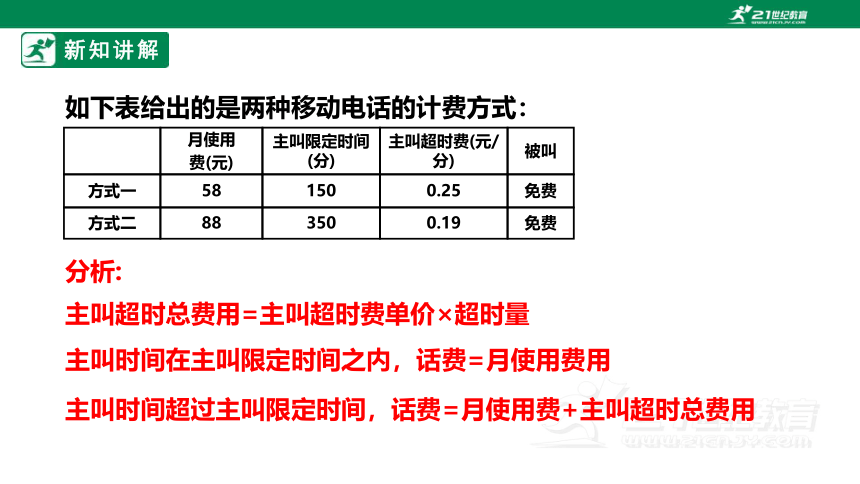
如下表给出的是两种移动电话的计费方式:
主叫时间超过主叫限定时间,话费=月使用费+主叫超时总费用
主叫时间在主叫限定时间之内,话费=月使用费用
主叫超时总费用=主叫超时费单价×超时量
新知讲解
分析:
(2).主叫超时费0.25元/min高于0.19元/min,说明超过限定时间后,方式一比方式二的每分钟的收费高.
(1). 主叫限定时间150min小于350min,说明方式一主叫限定时间少于方式二的;
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
如下表给出的是两种移动电话的计费方式:
新知讲解
(1)当t在不同时间范围内取值时, 方式一和方式二计费如下表.
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
58+0.25(t-150)
88
58+0.25(350-150)=108
88
58+0.25(t-150)
88+0.19(t-350)
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
新知讲解
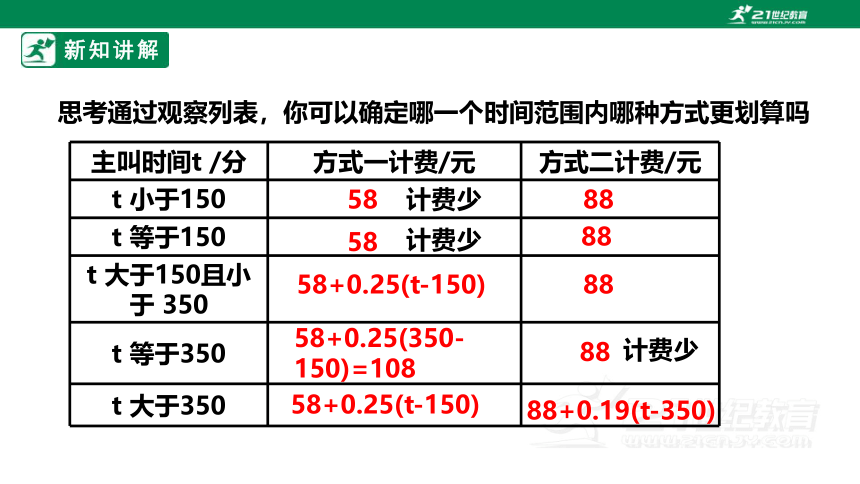
思考通过观察列表,你可以确定哪一个时间范围内哪种方式更划算吗
计费少
计费少
计费少
58
88
58
88
58+0.25(t-150)
88
58+0.25(350-150)=108
88
58+0.25(t-150)
88+0.19(t-350)
新知讲解
你认为选择哪种计费方式更省钱(设一个月通话分钟数为t,t取正整数)
观察右表得出:
①t小于或等于150时,按方式一的计费小.
问:当t大于150且小于350时和t大于350时这两个时间范围内的情况是怎样的呢
新知讲解
思考:当t大于150且小于350时,两种计费方式哪种更划算呢
解∶58+0.25(t-150)=88
58+0.25t-37.5=88
0.25t=67.5
t=270
当t=270min时,两种计费方式的费用相等,都是88元.
新知讲解
结论:
①当t=270分钟时,方式一和方式二资费 .
②当150③当270相同
方式一划算
方式二划算
新知讲解
思路:当t大于350时,方式一的计费可以写成108+0.25(t-350)(此时相当月租费为108元,超时部分按0.25收费)
方式一收费: 108+0.25(t-350)
方式二收费: 88+0.19(t-350)
方式一大于方式二资费,方式二划算
因为[108+0.25(t-350)] –[88+0.19(t-350)]>0
讨论:t大于350
新知讲解
综合以上的分析,可以发现:
t小于270时,选择方式一省钱;
t大于270时,选择方式二省钱.
t等于270时,两种方式的计费相等.
解决最优方案问题时,一般采用以下步骤∶
①设未知数;
②列式;
③比较方案;
④决定取舍,
即根据比较结果确定最优方案.
归纳
课堂练习
1. 周末,小明的妈妈让他到药店购买口罩和酒精湿巾,已知口罩每包3元,酒精湿巾每包2元,共用了30元钱(两种物品都买),小明的购买方案共有( )
A. 3种 B. 4种 C. 5种 D. 6种
B
课堂练习
2. 某超市在“元旦”活动期间,推出如下购物优惠方案:
①一次性购物在100元(不含100元)以内,不享受优惠;②一次性购物在100元(含100元)以上,350元(不含350元)以内,一律享受九折优惠;③一次性购物在350元(含350元)以上,一律享受八折优惠;小敏在该超市两次购物分别付了85元和270元,如果小敏把这两次购物改为一次性购物,则小敏至少需付款( )元
A. 284 B. 308 C. 312 D. 320
B
课堂练习
3. 假期张老师和王老师带学生乘车外出参加实践活动,甲车主说“每人8折”,乙车主说“学生9折,老师减半”,张老师计算了一下,不论坐谁的车,费用都一样,则张老师和王老师带的学生人数为( )
A. 6名 B. 7名 C. 8名 D. 9名
A
课堂练习
4. .甲、乙、丙三家超市为了促销一种定价为m元的商品,甲超市连续两次降价20%;乙超市一次性降价40%;丙超市第一次降价30%,第二次降价10%,此时顾客要购买这种商品,最划算的超市是( )
A. 甲 B. 乙 C. 丙 D. 三家都一样
B
课堂练习
5. 小明和爸爸妈妈三人暑假准备参加旅游团去北京旅游,甲旅行社说:“如果父母买全票,小孩可半价优惠”:乙旅行社说:“全部按全票价的 8 折优惠”, 若全票价为1200元,则小明应选择哪家旅行社( )
选择甲 B. 选择乙
C. 选择甲、乙都一样 D. 无法确定
B
6. 周末,小康一家和姑姑一家(共6人)相约一起去观看电影《长津湖》.小康用手机查到家附近两家影城的票价和优惠活动如下:
小康利用网络给所有人都购了票,他发现在两家影城购票的总费用相同,则购票的总费用是多少元,两家共有学生多少人.
课堂练习
影城 票价(元) 优惠活动
时光影城 48 学生票半价
遇见影城 50 网络购票,总价打八折
课堂练习
解:共有6人看电影,根据“遇见影城”的优惠方式总费用为:
50×6×80%=240(元),
∴购票的总费用是240元;
设6人中学生x人,则成年人(6-x)人,
根据“时光影城”的优惠方式计算费用得:
1/2×48x+48×(6-x)=240 ,
解得:x=2 ,
∴两家共有学生2人;
课堂练习
7. 某果蔬基地现有草莓18吨,若在市场上直接销售鲜草莓,每吨可获利润500元;若对草莓进行粗加工,每吨可获利润1200元;若对草莓进行精加工,每吨可获利润2000元.该工厂的生产能力是如果对草莓进行粗加工,每天可加工3吨;精加工,每天可加工1吨,受人员限制,两种加工方式不能同时进行;受气候限制,这批草莓必须在8天内全部销售或加工完毕,为此,该厂设计了两种方案。方案一,尽可能多的精加工,其余的草莓直接销售;方案二:将一部分草莓精加工,其余的粗加工销售,并恰好在8天完成,你认为哪种方案获利较多?为什么?
课堂练习
解:方案二获利较多,理由如下:
方案一获利: 8×1×2000+(18-8)×500=21000 (元),
方案二:设 x 天精加工草莓,则 (8-x) 天粗加工草莓,
x+3(8-x)=18
x=3
则 8-3=5 (天)
获利: 3×2000+5×3×1200=24000 (元)
∵ 24000>21000 ,
∴方案二获利较多
课堂练习
8. 这个星期周末,七年级准备组织观看电影《我和我的祖国》,由各班班长负责买票,每班人数都多于50人,票价每张20元,一班班长问售票员买团体票是否可以优惠,售票员说:50人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;方案2:若打9折,有7人可以免票.
(Ⅰ)2班有61名学生,他该选择哪个方案?
(Ⅱ)一班班长思考一会儿说我们班无论选择哪种方案要付的钱是一样的,问你知道一班有几人吗?
课堂练习
解:(Ⅰ)∵方案一:61×20×0.8=976(元),
方案二:(61﹣7)×0.9×20=972(元),
∴选择方案二.
(Ⅱ)假设1班有x人,根据题意得出:
x×20×0.8=(x﹣7)×0.9×20,
解得:x=63,
答:1班有63人.
课堂总结
解决最优方案问题时,一般采用以下步骤∶
①设未知数;
②列式;
③比较方案;
④决定取舍,
即根据比较结果确定最优方案.
作业布置
第107页习题3.4
第8、9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4实际应用与一元一次方程
人教版七年级上册
教学目标
1.经历在消费过程中选择哪种消费方案的过程,掌握一些特殊的解决这类问题的方法.
2. 培养学生的分析能力和解决实际问题的能力,体会合作学习在解决问题过程中的重要意义.
3. 感受所学知识与现实生活的联系,从中获得价值体验;让学生在解决问题的过程中获得成功体验,增强学生学好数学的信心.
教学重点∶掌握解决这类问题的基本方法.
教学难点:是会运用一元一次方程解决问题.
新知导入
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
如下表给出的是两种移动电话的计费方式:
考虑下列问题:
(1). 设一个月内用移动电话主叫为狋min(t是正整数).根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费
电话计费问题:
新知讲解
分析:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
如下表给出的是两种移动电话的计费方式:
主叫时间超过主叫限定时间,话费=月使用费+主叫超时总费用
主叫时间在主叫限定时间之内,话费=月使用费用
主叫超时总费用=主叫超时费单价×超时量
新知讲解
分析:
(2).主叫超时费0.25元/min高于0.19元/min,说明超过限定时间后,方式一比方式二的每分钟的收费高.
(1). 主叫限定时间150min小于350min,说明方式一主叫限定时间少于方式二的;
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
如下表给出的是两种移动电话的计费方式:
新知讲解
(1)当t在不同时间范围内取值时, 方式一和方式二计费如下表.
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
58+0.25(t-150)
88
58+0.25(350-150)=108
88
58+0.25(t-150)
88+0.19(t-350)
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
新知讲解
思考通过观察列表,你可以确定哪一个时间范围内哪种方式更划算吗
计费少
计费少
计费少
58
88
58
88
58+0.25(t-150)
88
58+0.25(350-150)=108
88
58+0.25(t-150)
88+0.19(t-350)
新知讲解
你认为选择哪种计费方式更省钱(设一个月通话分钟数为t,t取正整数)
观察右表得出:
①t小于或等于150时,按方式一的计费小.
问:当t大于150且小于350时和t大于350时这两个时间范围内的情况是怎样的呢
新知讲解
思考:当t大于150且小于350时,两种计费方式哪种更划算呢
解∶58+0.25(t-150)=88
58+0.25t-37.5=88
0.25t=67.5
t=270
当t=270min时,两种计费方式的费用相等,都是88元.
新知讲解
结论:
①当t=270分钟时,方式一和方式二资费 .
②当150
方式一划算
方式二划算
新知讲解
思路:当t大于350时,方式一的计费可以写成108+0.25(t-350)(此时相当月租费为108元,超时部分按0.25收费)
方式一收费: 108+0.25(t-350)
方式二收费: 88+0.19(t-350)
方式一大于方式二资费,方式二划算
因为[108+0.25(t-350)] –[88+0.19(t-350)]>0
讨论:t大于350
新知讲解
综合以上的分析,可以发现:
t小于270时,选择方式一省钱;
t大于270时,选择方式二省钱.
t等于270时,两种方式的计费相等.
解决最优方案问题时,一般采用以下步骤∶
①设未知数;
②列式;
③比较方案;
④决定取舍,
即根据比较结果确定最优方案.
归纳
课堂练习
1. 周末,小明的妈妈让他到药店购买口罩和酒精湿巾,已知口罩每包3元,酒精湿巾每包2元,共用了30元钱(两种物品都买),小明的购买方案共有( )
A. 3种 B. 4种 C. 5种 D. 6种
B
课堂练习
2. 某超市在“元旦”活动期间,推出如下购物优惠方案:
①一次性购物在100元(不含100元)以内,不享受优惠;②一次性购物在100元(含100元)以上,350元(不含350元)以内,一律享受九折优惠;③一次性购物在350元(含350元)以上,一律享受八折优惠;小敏在该超市两次购物分别付了85元和270元,如果小敏把这两次购物改为一次性购物,则小敏至少需付款( )元
A. 284 B. 308 C. 312 D. 320
B
课堂练习
3. 假期张老师和王老师带学生乘车外出参加实践活动,甲车主说“每人8折”,乙车主说“学生9折,老师减半”,张老师计算了一下,不论坐谁的车,费用都一样,则张老师和王老师带的学生人数为( )
A. 6名 B. 7名 C. 8名 D. 9名
A
课堂练习
4. .甲、乙、丙三家超市为了促销一种定价为m元的商品,甲超市连续两次降价20%;乙超市一次性降价40%;丙超市第一次降价30%,第二次降价10%,此时顾客要购买这种商品,最划算的超市是( )
A. 甲 B. 乙 C. 丙 D. 三家都一样
B
课堂练习
5. 小明和爸爸妈妈三人暑假准备参加旅游团去北京旅游,甲旅行社说:“如果父母买全票,小孩可半价优惠”:乙旅行社说:“全部按全票价的 8 折优惠”, 若全票价为1200元,则小明应选择哪家旅行社( )
选择甲 B. 选择乙
C. 选择甲、乙都一样 D. 无法确定
B
6. 周末,小康一家和姑姑一家(共6人)相约一起去观看电影《长津湖》.小康用手机查到家附近两家影城的票价和优惠活动如下:
小康利用网络给所有人都购了票,他发现在两家影城购票的总费用相同,则购票的总费用是多少元,两家共有学生多少人.
课堂练习
影城 票价(元) 优惠活动
时光影城 48 学生票半价
遇见影城 50 网络购票,总价打八折
课堂练习
解:共有6人看电影,根据“遇见影城”的优惠方式总费用为:
50×6×80%=240(元),
∴购票的总费用是240元;
设6人中学生x人,则成年人(6-x)人,
根据“时光影城”的优惠方式计算费用得:
1/2×48x+48×(6-x)=240 ,
解得:x=2 ,
∴两家共有学生2人;
课堂练习
7. 某果蔬基地现有草莓18吨,若在市场上直接销售鲜草莓,每吨可获利润500元;若对草莓进行粗加工,每吨可获利润1200元;若对草莓进行精加工,每吨可获利润2000元.该工厂的生产能力是如果对草莓进行粗加工,每天可加工3吨;精加工,每天可加工1吨,受人员限制,两种加工方式不能同时进行;受气候限制,这批草莓必须在8天内全部销售或加工完毕,为此,该厂设计了两种方案。方案一,尽可能多的精加工,其余的草莓直接销售;方案二:将一部分草莓精加工,其余的粗加工销售,并恰好在8天完成,你认为哪种方案获利较多?为什么?
课堂练习
解:方案二获利较多,理由如下:
方案一获利: 8×1×2000+(18-8)×500=21000 (元),
方案二:设 x 天精加工草莓,则 (8-x) 天粗加工草莓,
x+3(8-x)=18
x=3
则 8-3=5 (天)
获利: 3×2000+5×3×1200=24000 (元)
∵ 24000>21000 ,
∴方案二获利较多
课堂练习
8. 这个星期周末,七年级准备组织观看电影《我和我的祖国》,由各班班长负责买票,每班人数都多于50人,票价每张20元,一班班长问售票员买团体票是否可以优惠,售票员说:50人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;方案2:若打9折,有7人可以免票.
(Ⅰ)2班有61名学生,他该选择哪个方案?
(Ⅱ)一班班长思考一会儿说我们班无论选择哪种方案要付的钱是一样的,问你知道一班有几人吗?
课堂练习
解:(Ⅰ)∵方案一:61×20×0.8=976(元),
方案二:(61﹣7)×0.9×20=972(元),
∴选择方案二.
(Ⅱ)假设1班有x人,根据题意得出:
x×20×0.8=(x﹣7)×0.9×20,
解得:x=63,
答:1班有63人.
课堂总结
解决最优方案问题时,一般采用以下步骤∶
①设未知数;
②列式;
③比较方案;
④决定取舍,
即根据比较结果确定最优方案.
作业布置
第107页习题3.4
第8、9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
