五年级数学北师大版上册 六.组合图形的面积 课件(共23张PPT)
文档属性
| 名称 | 五年级数学北师大版上册 六.组合图形的面积 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 626.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-07 16:55:50 | ||
图片预览




文档简介
(共23张PPT)
组合图形的面积
单元复习
学习目标:
1、掌握组合图形面积的计算方法。
2、能根据各种组合图形的条件,把组合图形转化为已经学过的基本图形,有效地选择计算方法并能正确地解答。
填一填:
① 长方形的面积 =
②正方形的面积 =
③ 平行四边形的面积 =
④三角形的面积 =
⑤梯形的面积 =
长×宽
边长×边长
底×高
底×高÷2
(上底+下底)×高÷2
知识回顾(3分钟)
天宫一号
像这样由几个简单的基本图形
组合而成的图形叫做组合图形
教学导入
像这样由几个简单的基本图形
组合而成的图形叫做组合图形
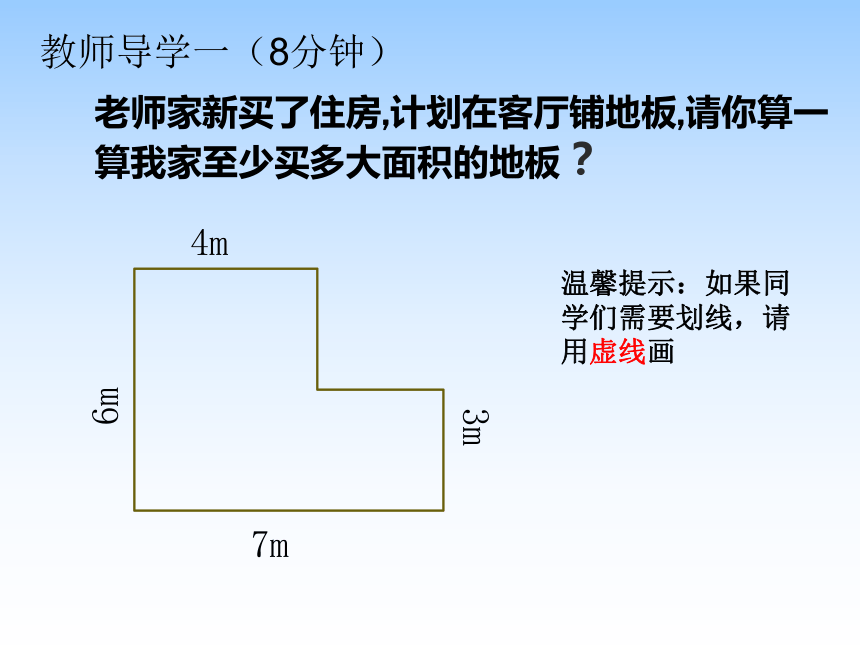
老师家新买了住房,计划在客厅铺地板,请你算一算我家至少买多大面积的地板?
4m
6m
3m
7m
教师导学一(8分钟)
温馨提示:如果同学们需要划线,请用虚线画
3m
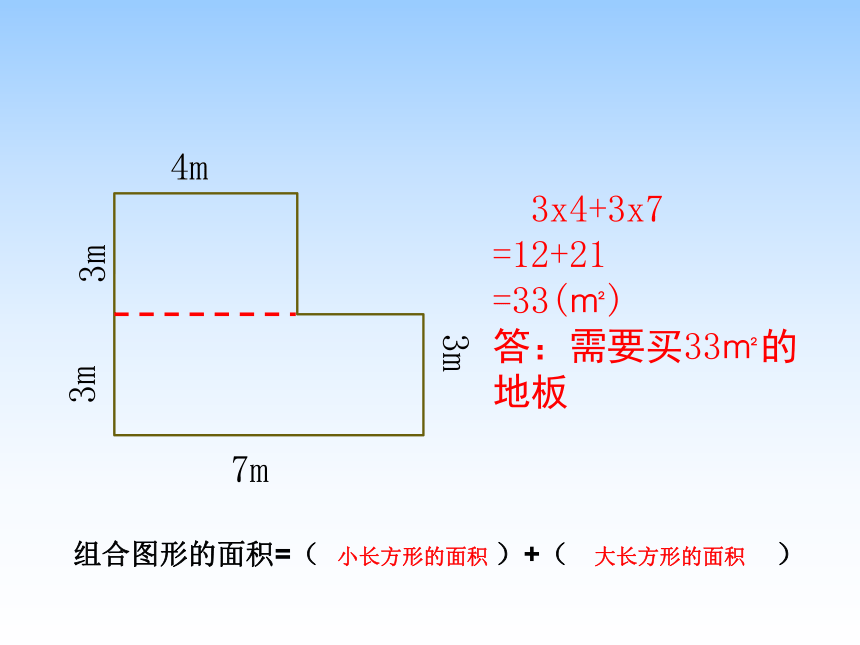
3x4+3x7
=12+21
=33(㎡)
答:需要买33㎡的地板
4m
3m
7m
3m
组合图形的面积=( )+( )
小长方形的面积
大长方形的面积
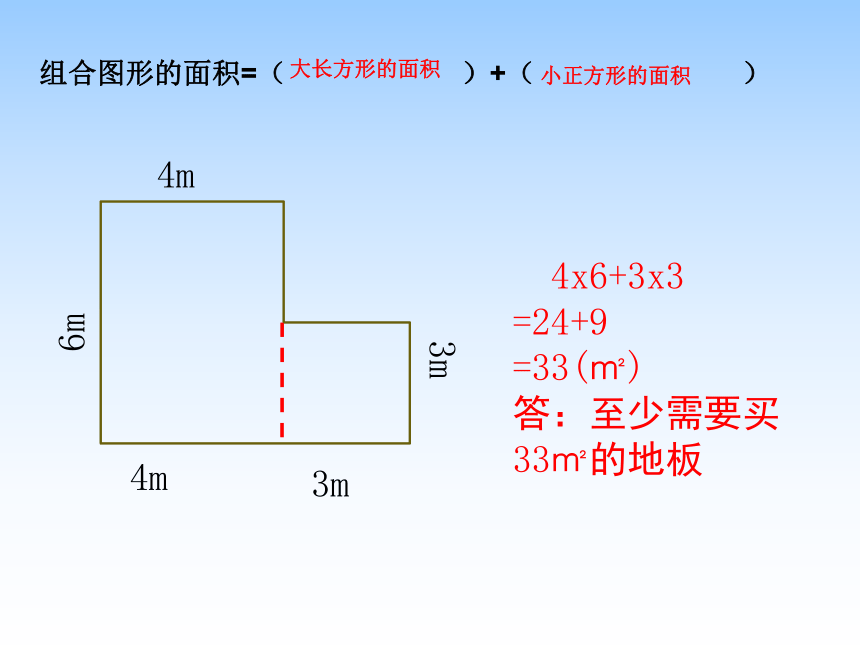
4x6+3x3
=24+9
=33(㎡)
答:至少需要买33㎡的地板
4m
6m
3m
4m
3m
组合图形的面积=( )+( )
大长方形的面积
小正方形的面积
4m
6m
3m
7m
3m
3m
(3+6)x4÷2+(3+7)x3÷2
=36÷2+30÷2
=33(㎡)
答:至少需要买33㎡的地板
组合图形的面积=( )+( )
梯形的 面积
梯形的 面积
分割法
计算组合图形的面积,一般是把它们分割成基本图形,如长方形、正方形、三角形、梯形等,再计算它们的面积。
6x7—3x3
=42—9
=33(㎡)
答:至少需要买33㎡的地板
6m
3m
7m
3m
3m
组合图形的面积=( )—( )
大长方形的面积
小正方形的面积
添补法
6m
3m
7m
3m
1.下面各个图形可以分成哪些已经学过的图形
效果检测1(6分钟)
效果检测2
一
15×20+20×12÷2
=300+120
=420(平方厘米)
10+18+10=38(厘米)
(18+38)×25÷2=700(平方厘米)
700-18×10=520(平方厘米)
方法指导:组合图形的面积=(三角形的面积)+(平行四边形的面积)
方法指导:组合图形的面积=(梯形的面积)-(长方形的面积)
10cm
20cm
5cm
10cm
计算这个组合图形的面积
10-5=5(cm)
10x5+(10+20)x5÷2
=50+75
=125(c㎡)
答:这个图形的面积是125c㎡
教师导学二(3分钟)
方法指导:组合图形的面积=(长方形的面积)+(梯形的面积)
如图,有一面墙,粉刷这面墙每平方米需要 0.15千克涂料,一共需要多少千克涂料
4x10+1.6x10÷2
=40+16÷2
=40+8
=48(㎡) 48x0.15=7.2(千克)
答:一共需要7.2千克涂料。
4m
10m
1.6m
效果检测(3分钟)
方法指导:组合图形的面积=(三角形的面积)+(长方形的面积)
2、 如图,一张硬纸板剪下4个边长是4厘米的小正方形后,可以做成一个没有盖子的盒子.这张硬纸板还剩下多大的面积
26cm
20cm
20x26—4x4x4
=520—16x4
=520—64
=456(c㎡)
答:这张硬纸还剩下456 c㎡
方法指导:硬纸板的面积=(大长方形的面积)—(4个小正方形的面积)
综合检测(3分钟)
总结:
计算组合图形的面积,一般把它们分割或添补成基本图形,如长方形、正方形、三角形、梯形等,再计算它们的面积。
×100
平方厘米
平方分米
平方米
公 顷
平方千米
×100
×10000
×100
知识回顾
1000000
100
再见
组合图形的面积
单元复习
学习目标:
1、掌握组合图形面积的计算方法。
2、能根据各种组合图形的条件,把组合图形转化为已经学过的基本图形,有效地选择计算方法并能正确地解答。
填一填:
① 长方形的面积 =
②正方形的面积 =
③ 平行四边形的面积 =
④三角形的面积 =
⑤梯形的面积 =
长×宽
边长×边长
底×高
底×高÷2
(上底+下底)×高÷2
知识回顾(3分钟)
天宫一号
像这样由几个简单的基本图形
组合而成的图形叫做组合图形
教学导入
像这样由几个简单的基本图形
组合而成的图形叫做组合图形
老师家新买了住房,计划在客厅铺地板,请你算一算我家至少买多大面积的地板?
4m
6m
3m
7m
教师导学一(8分钟)
温馨提示:如果同学们需要划线,请用虚线画
3m
3x4+3x7
=12+21
=33(㎡)
答:需要买33㎡的地板
4m
3m
7m
3m
组合图形的面积=( )+( )
小长方形的面积
大长方形的面积
4x6+3x3
=24+9
=33(㎡)
答:至少需要买33㎡的地板
4m
6m
3m
4m
3m
组合图形的面积=( )+( )
大长方形的面积
小正方形的面积
4m
6m
3m
7m
3m
3m
(3+6)x4÷2+(3+7)x3÷2
=36÷2+30÷2
=33(㎡)
答:至少需要买33㎡的地板
组合图形的面积=( )+( )
梯形的 面积
梯形的 面积
分割法
计算组合图形的面积,一般是把它们分割成基本图形,如长方形、正方形、三角形、梯形等,再计算它们的面积。
6x7—3x3
=42—9
=33(㎡)
答:至少需要买33㎡的地板
6m
3m
7m
3m
3m
组合图形的面积=( )—( )
大长方形的面积
小正方形的面积
添补法
6m
3m
7m
3m
1.下面各个图形可以分成哪些已经学过的图形
效果检测1(6分钟)
效果检测2
一
15×20+20×12÷2
=300+120
=420(平方厘米)
10+18+10=38(厘米)
(18+38)×25÷2=700(平方厘米)
700-18×10=520(平方厘米)
方法指导:组合图形的面积=(三角形的面积)+(平行四边形的面积)
方法指导:组合图形的面积=(梯形的面积)-(长方形的面积)
10cm
20cm
5cm
10cm
计算这个组合图形的面积
10-5=5(cm)
10x5+(10+20)x5÷2
=50+75
=125(c㎡)
答:这个图形的面积是125c㎡
教师导学二(3分钟)
方法指导:组合图形的面积=(长方形的面积)+(梯形的面积)
如图,有一面墙,粉刷这面墙每平方米需要 0.15千克涂料,一共需要多少千克涂料
4x10+1.6x10÷2
=40+16÷2
=40+8
=48(㎡) 48x0.15=7.2(千克)
答:一共需要7.2千克涂料。
4m
10m
1.6m
效果检测(3分钟)
方法指导:组合图形的面积=(三角形的面积)+(长方形的面积)
2、 如图,一张硬纸板剪下4个边长是4厘米的小正方形后,可以做成一个没有盖子的盒子.这张硬纸板还剩下多大的面积
26cm
20cm
20x26—4x4x4
=520—16x4
=520—64
=456(c㎡)
答:这张硬纸还剩下456 c㎡
方法指导:硬纸板的面积=(大长方形的面积)—(4个小正方形的面积)
综合检测(3分钟)
总结:
计算组合图形的面积,一般把它们分割或添补成基本图形,如长方形、正方形、三角形、梯形等,再计算它们的面积。
×100
平方厘米
平方分米
平方米
公 顷
平方千米
×100
×10000
×100
知识回顾
1000000
100
再见
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
