苏教版(2019)高中数学必修第一册 学案1.1 《集合的概念与表示》课时同步(含答案)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 学案1.1 《集合的概念与表示》课时同步(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 862.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-07 19:37:54 | ||
图片预览




文档简介
《集合的概念与表示》课时同步解
问题情境导入
军训时,教官发出口令:“高一(1)班同学集合”,高一(1)班的全体同学就会从四面八方聚集到教官身边来,不是高一(1)班的同学就会自动走开,这时教官的一声“集合”就把“一些确定的不同对象汇集在一起了”.如果教官高喊:“高一(1)班的高个子同学‘集合’”,高一(1)班的每个同学是否知道自己该不该过去?学习本节课后,你就能非常清晰方便地表述上面的问题了.
新课自主学习
自学导引
1.一般地,一定范围内某些确定的、不同的对象的全体组成一个________.集合中的每一个对象称为该集合的__________,简称__________.
2.如果a是集合A的元素,就说a_________集合A,记作a________A;如果a不是集合A的元素,就说a________集合A,记作a________A,或a________A.
3.数学中一些常用的数集及其记法:全体自然数组成的集合称为自然数集,记作__________;所有正整数组成的集合称为正整数集,记作_________或_________;全体整数组成的集合称为整数集,记作_________;全体有理数组成的集合称为有理数集,记作_________;全体实数组成的集合称为实数集,记作_________.
4.将集合的元素一一列举出来,并置于花括号“{}”内,这种方法叫_________.用这种方法表示集合,元素之间要用隔开,但列举时与元素的次序_________.
5.将集合的所有元素都具有的性质(满足的条件)表示出来,写成的形式,这种方法叫__________.
6.画一条封闭的曲线,用它的内部表示一个集合,这种方法叫__________图法.
7.如果两个集合所含的元素完全相同(即A中的元素都是B的元素,B中的元素也都是A的元素),那么称这两个集合__________.
8.含有有限个元素的集合,称为________,含有无限个元素的集合,称为__________.不含任何元素的集合称为__________,记作_________.
答案
1.集合 元素 元
属于 不属于
3.
4.列举法 逗号 无关
5.描述法
6.Venn
7.相等
8.有限集 无限 集空
预习测评
1.用“”或“”填空:
1_____N,_______Q,________R.
2.小于5的自然数组成的集合可表示为__________.
3.方程的解集为__________.
4.集合与集合相等吗?__________.
5.用列举法表示出__________.
答案
1.
2.
3.
4.相等
5..
新知合作探究
探究点1 集合的概念
知识详解
1.一般地,一定范围内某些确定的、不同的对象的全体组成一个集合,集合中的每一个对象称为该集合的元素,简称元.
2.集合中的元素具有确定性、互异性、无序性三大特征.
(1)确定性:集合中的元素是确定的,即任何一个对象都能说明它是或不是某个集合的元素,两种情况必居其一且仅居其一,不会模棱两可例如“著名科学家”“与接近的数”等都不能组成一个集合.
(2)互异性:一个给定的集合中的元素是互不相同的,即同一元素在同一集合中,不能重复出现例如:某集合是由这三个元素构成的,是错误说法.
只要构成两个集合的元素是一样的,这两个集合就是相等的.
(3)无序性:在一个集合中,元素之间都是平等的,它们都充当集合中的一员,无先后次序之说例如,由1,2,3构成的集合与由3,2,1构成的集合是相同的集合.
特别提示
集合中的元素的三个基本特征是集合本质属性的反映,利用集合中元素的三个基本特征,一方面可以判断一些对象是否能构成集合,另一方面可以解决与集合有关的问题.
3.常用的数集
全体自然数组成的集合,叫作自然数集,记作N.
全体正整数组成的集合,叫作正整数集,记作或.
全体整数组成的集合,叫作整数集,记作Z.
全体有理数组成的集合,叫作有理数集,记作Q.
全体实数组成的集合,叫作实数集,记作R.
4.如果两个集合所含的元素完全相同(即A中的元素都是B的元素,B中的元素也都是A的元素),那么称这两个集合相等.
5.集合的分类:
有限集:含有有限个元素的集合称为有限集.
无限集:含有无限个元素的集合称为无限集.
空集:不含任何元素的集合称为空集,记为.
典例探究
例1 判断下列每组对象能否构成集合:
(1)美丽的小鸟;
(2)方程在实数范围内的解;
(3)第1章中的所有难题;
(4)高一(2)班的高个子的同学;
(5)所有的平行四边形;
(6)高一(2)班所有高于1.70米的同学.
解析 根据集合中元素的确定性判断.
答案 (1)“美丽的小鸟”没有一个明确的标准去判断某只小鸟是否美丽,不符合集合中元素的确定性,所以“美丽的小鸟”不能构成一个集合;同理(3)中没有一个标准去判断某道题是否是难题,(4)没有一个标准判断某个同学个子高还是矮,故(3)(4)不能构成集合.(2)方程的两根2和是确定的,能构成一个集合,(5)(6)中的对象也是确定的,故也能构成集合.
方法归纳 集合是一组确定的对象的全体.一般地,判断一组对象能否构成集合,关键是看给定对象是否具有一个确定的特征,如果有,能构成集合,如果没有,就不能构成集合,如本例中的(4),是否是高个子,没有标准去判断,故这一组对象就不能构成集合.
变式训练1 在“①高一数学教材中的中档题;②所有的正三角形;③方程的实数解”中,能够组成集合的是( )
A.②
B.③
C.②③
D.①②③
答案 C
点拨 能否组成集合,关键看对给定对象的判断标准是否明确,①的“中档题”没有明确的标准,故不能组成集合.
探究点2 集合与元素的关系
知识详解
我们常用大写拉丁字母等表示集合,用小写拉丁字母等表示集合中的元素.元素与集合之间有两种关系:如果a是集合A的元素,就说a属于集合A,记作;如果a不是集合A的元素,就说a不属于集合A,记作或.
特别提示
(1)符号“”“”(或“”)是表示元素与集合之间关系的,不能用来表示集合与集合之间的关系.
(2)与取决于a是不是集合A的元素.根据集合中元素的确定性,可知对任何a与A,与(或)这两种情况中必有一种且只有一种成立.
典例探究
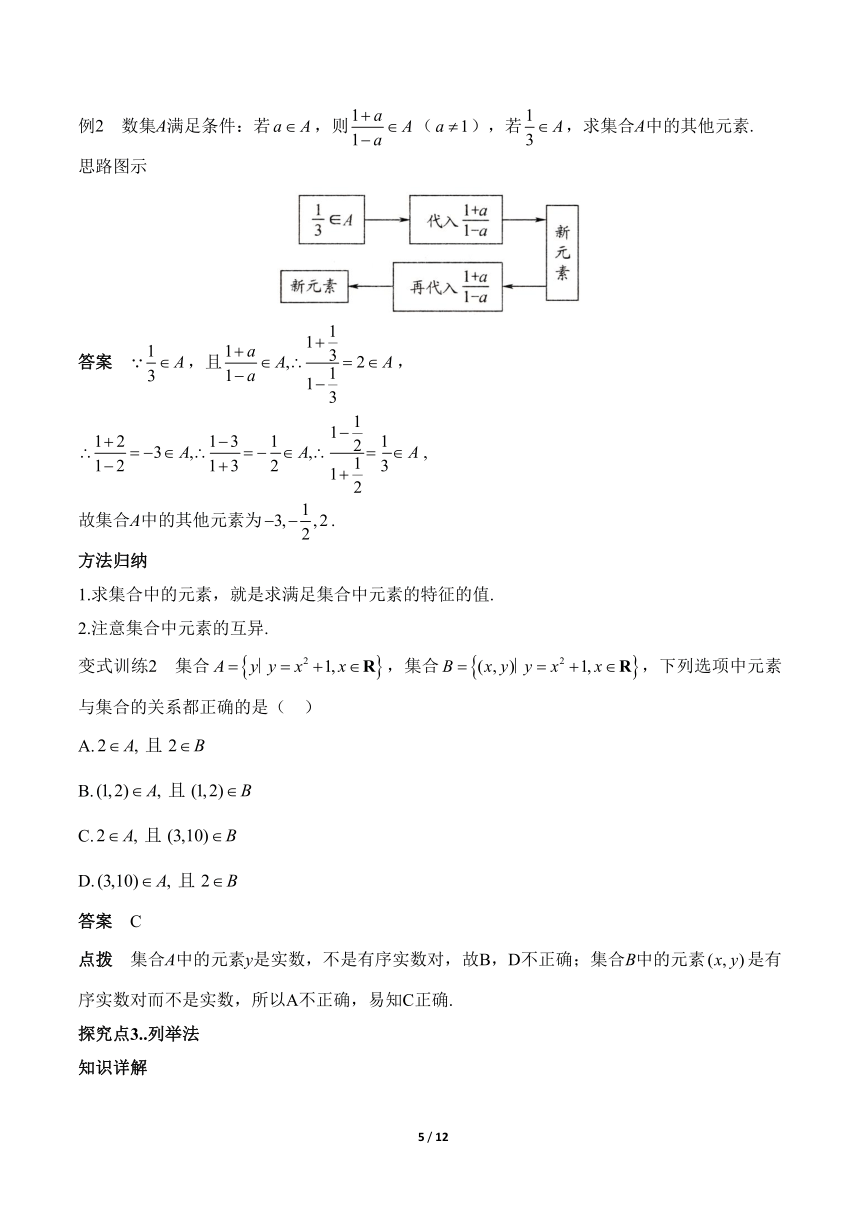
例2 数集A满足条件:若,则(),若,求集合A中的其他元素.
思路图示
答案 ,且,
,
故集合A中的其他元素为.
方法归纳
1.求集合中的元素,就是求满足集合中元素的特征的值.
2.注意集合中元素的互异.
变式训练2 集合,集合,下列选项中元素与集合的关系都正确的是( )
A.
B.
C.
D.
答案 C
点拨 集合A中的元素y是实数,不是有序实数对,故B,D不正确;集合B中的元素是有序实数对而不是实数,所以A不正确,易知C正确.
探究点3..列举法
知识详解
1.将集合的元素一一列举出来,并置于花括号“{}”内,这种表示集合的方法叫作列举法例如,“小于10的所有自然数组成的集合”表示为.
2.一般情况下,对于有限集,在元素不太多的情况下宜采用列举法,它具有直观明了的特点.
3.用列举法表示集合时,应注意:①元素间用“,”分隔;②集合中的元素要具有确定性、互异性、无序性三个特性;③若元素个数较多或无限个且构成集合的这些元素有明显规律,在不发生误解的情况下,也可用列举法,但必须把元素规律显示清楚后才能用省略号.如不超过100的正整数构成的集合可表示为.
典例探究
例3 已知集合是小于6的正整数,是小于10的质数,是24和36的公约数,用列举法表示下列集合:
(1);
(2).
解析 要求的集合M与N中的元素与集合有关,先将集合用列举法表示,然后求解.
答案 集合.
(1),且.
(2),且.
方法归纳 解此题的关键是理解M的元素既是A的元素又是C的元素,N的元素是B的元素但不是C的元素,这体现了符号语言和文字语言的互译.
变式训练3 设a,b都是非零实数,所有可能的值组成的集合是( )
A.
B.
C.
D.
答案 D
点拨 因为的结果是1还是,取决于x的正负,所以本题应从a,b的正负来分类讨论,共有四种情况,讨论得出结果,注意集合的元素不能重复.
探究点4 描述法
知识详解
1.将集合的所有元素都具有的性质(满足的条件)表示出来,写成的形式,这样的方法称为描述法.具体方法是:在花括号内先写上表示这个集合的元素的般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征.
描述法的语言形式有三种:文字语言、符号语言、图形语言.
2.对无限集,一般采用描述法表示.它的优点是形式简洁,能充分体现集合中元素的特征.
3.使用描述法时,应注意六点:
①写清楚集合中元素的代表符号;
②说明该集合中元素的性质;
③不能出现未被说明的字母;
④多层描述时,应当准确使用“且”“或”;
⑤所有描述的内容都要写在括号内;
⑥用于描述的语句力求简明、确切.
典例探究
例4 用描述法表示下列集合:
(1);
(2);
(3)正偶数集;
(4)被3除余2的正整数组成的集合;
(5)平面直角坐标系中坐标轴上的点组成的集合;
(6).
解析 根据描述法的形式要求改写表示方法.
答案 (1)可表示为.
(2)可表示为.
(3)可表示为.
偶数用式子可表示为,但此题要求x为正偶数,故.
(4)可表示为.
设被3除余2的数为x,则,但此题要求x为正整数,故,,也可以写成,,注意此时n从1开始.
(5)可表示为.
此集合是点集,坐标轴上的点的特征是横、纵坐标中至少有一个为0,即.
(6)可表示为.
集合中各元素为正整数的平方,故各元素可表示为,也可以写成.
方法归纳 用描述法表示集合的基本步骤:(1)弄清元素的形式;(2)写出代表元素,写在“”前面;(3)确定元素所具有的属性,写在“”的后面;(4)用花括号把它们括起来.
变式训练4 把下列用描述法表示的集合用列举法表示:
(1);
(2).
答案 (1),
.
(2).
,即.
.
点拨 集合M中的代表元素是,集合N中的代表元素是,而不是x,同时要注意(1)中,,(2)中等约束条件.
易错易混解读
例 已知集合,且,则x的值为( )
A.
B.3
C.或3
D.
错解 C
错因分析 该题易错选C,原因是忽略了检验集合元素的互异性,导致多选了.
正解 ,
.
当时,,不满足互异性,故;
当时,解得(舍去),当时,集合,符合题意,.
答案 A
纠错心得 当集合中的元素含有字母时,求出参数后,一定要代回检验,确保满足集合元素的互异性.
课堂快速检测
一、选择题
1.下列各组对象能构成集合的有( )
①接近于0的实数;②小于0的实数;③与;④1,2,3.
A.1组
B.2组
C.3组
D.4
2.下列集合中与是同一集合的是( )
A.
B.
C.
D.
3.已知,且,则a的值为( )
A.0
B.1
C.2
D.3
4.已知集合中的三个元素是的三边长,那么一定不是( )
A.锐角三角形
B直角三角形
C.钝角三角形
D.等腰三角形
5.下列集合恰有两个元素的是( )
A.
B.
C.
D.
二、解答题
6.用适当的方法表示下列集合
(1)大于小于12.8的整数的全体;
(2)梯形的全体构成的集合;
(3)所有能被3整除的数的集合;
(4)方程的解集;
(5)不等式的解集.
答案
1.
答案:C
解析:①中“接近于0”不是一个明确的标准,不满足集合中元素的确定性,所以不能构成集合;②中“小于0”是个明确的标准,能构成集合;③中与是两个不同的对象,是确定的,能构成集合,该集合有两个元素;④中的对象是确定的,可以构成集合,构成的集合为{1,2,3}.
2.
答案:D
解析:由集合中元素的无序性可知D正确.
3.
答案:D
解析:由元素与集合的关系知,.
4.
答案:D
解析:由集合中元素的互异性知互不相等,故选D.
5.
答案:C
解析:A表示只含有一个方程的集合;B表示函数中自变量的取值集合,有无数个元素;C表示方程的解集,有0,1两个元素;D表示函数的函数值的取值集合,有无数个元素.
6.
答案:见解析
解析:(1).
(2).
(3).
(4).
(5).
要点概括整合
1.本节知识导图:
2.这节课所涉及的方法有分类讨论和转化的数学思想方法.
1 / 12
问题情境导入
军训时,教官发出口令:“高一(1)班同学集合”,高一(1)班的全体同学就会从四面八方聚集到教官身边来,不是高一(1)班的同学就会自动走开,这时教官的一声“集合”就把“一些确定的不同对象汇集在一起了”.如果教官高喊:“高一(1)班的高个子同学‘集合’”,高一(1)班的每个同学是否知道自己该不该过去?学习本节课后,你就能非常清晰方便地表述上面的问题了.
新课自主学习
自学导引
1.一般地,一定范围内某些确定的、不同的对象的全体组成一个________.集合中的每一个对象称为该集合的__________,简称__________.
2.如果a是集合A的元素,就说a_________集合A,记作a________A;如果a不是集合A的元素,就说a________集合A,记作a________A,或a________A.
3.数学中一些常用的数集及其记法:全体自然数组成的集合称为自然数集,记作__________;所有正整数组成的集合称为正整数集,记作_________或_________;全体整数组成的集合称为整数集,记作_________;全体有理数组成的集合称为有理数集,记作_________;全体实数组成的集合称为实数集,记作_________.
4.将集合的元素一一列举出来,并置于花括号“{}”内,这种方法叫_________.用这种方法表示集合,元素之间要用隔开,但列举时与元素的次序_________.
5.将集合的所有元素都具有的性质(满足的条件)表示出来,写成的形式,这种方法叫__________.
6.画一条封闭的曲线,用它的内部表示一个集合,这种方法叫__________图法.
7.如果两个集合所含的元素完全相同(即A中的元素都是B的元素,B中的元素也都是A的元素),那么称这两个集合__________.
8.含有有限个元素的集合,称为________,含有无限个元素的集合,称为__________.不含任何元素的集合称为__________,记作_________.
答案
1.集合 元素 元
属于 不属于
3.
4.列举法 逗号 无关
5.描述法
6.Venn
7.相等
8.有限集 无限 集空
预习测评
1.用“”或“”填空:
1_____N,_______Q,________R.
2.小于5的自然数组成的集合可表示为__________.
3.方程的解集为__________.
4.集合与集合相等吗?__________.
5.用列举法表示出__________.
答案
1.
2.
3.
4.相等
5..
新知合作探究
探究点1 集合的概念
知识详解
1.一般地,一定范围内某些确定的、不同的对象的全体组成一个集合,集合中的每一个对象称为该集合的元素,简称元.
2.集合中的元素具有确定性、互异性、无序性三大特征.
(1)确定性:集合中的元素是确定的,即任何一个对象都能说明它是或不是某个集合的元素,两种情况必居其一且仅居其一,不会模棱两可例如“著名科学家”“与接近的数”等都不能组成一个集合.
(2)互异性:一个给定的集合中的元素是互不相同的,即同一元素在同一集合中,不能重复出现例如:某集合是由这三个元素构成的,是错误说法.
只要构成两个集合的元素是一样的,这两个集合就是相等的.
(3)无序性:在一个集合中,元素之间都是平等的,它们都充当集合中的一员,无先后次序之说例如,由1,2,3构成的集合与由3,2,1构成的集合是相同的集合.
特别提示
集合中的元素的三个基本特征是集合本质属性的反映,利用集合中元素的三个基本特征,一方面可以判断一些对象是否能构成集合,另一方面可以解决与集合有关的问题.
3.常用的数集
全体自然数组成的集合,叫作自然数集,记作N.
全体正整数组成的集合,叫作正整数集,记作或.
全体整数组成的集合,叫作整数集,记作Z.
全体有理数组成的集合,叫作有理数集,记作Q.
全体实数组成的集合,叫作实数集,记作R.
4.如果两个集合所含的元素完全相同(即A中的元素都是B的元素,B中的元素也都是A的元素),那么称这两个集合相等.
5.集合的分类:
有限集:含有有限个元素的集合称为有限集.
无限集:含有无限个元素的集合称为无限集.
空集:不含任何元素的集合称为空集,记为.
典例探究
例1 判断下列每组对象能否构成集合:
(1)美丽的小鸟;
(2)方程在实数范围内的解;
(3)第1章中的所有难题;
(4)高一(2)班的高个子的同学;
(5)所有的平行四边形;
(6)高一(2)班所有高于1.70米的同学.
解析 根据集合中元素的确定性判断.
答案 (1)“美丽的小鸟”没有一个明确的标准去判断某只小鸟是否美丽,不符合集合中元素的确定性,所以“美丽的小鸟”不能构成一个集合;同理(3)中没有一个标准去判断某道题是否是难题,(4)没有一个标准判断某个同学个子高还是矮,故(3)(4)不能构成集合.(2)方程的两根2和是确定的,能构成一个集合,(5)(6)中的对象也是确定的,故也能构成集合.
方法归纳 集合是一组确定的对象的全体.一般地,判断一组对象能否构成集合,关键是看给定对象是否具有一个确定的特征,如果有,能构成集合,如果没有,就不能构成集合,如本例中的(4),是否是高个子,没有标准去判断,故这一组对象就不能构成集合.
变式训练1 在“①高一数学教材中的中档题;②所有的正三角形;③方程的实数解”中,能够组成集合的是( )
A.②
B.③
C.②③
D.①②③
答案 C
点拨 能否组成集合,关键看对给定对象的判断标准是否明确,①的“中档题”没有明确的标准,故不能组成集合.
探究点2 集合与元素的关系
知识详解
我们常用大写拉丁字母等表示集合,用小写拉丁字母等表示集合中的元素.元素与集合之间有两种关系:如果a是集合A的元素,就说a属于集合A,记作;如果a不是集合A的元素,就说a不属于集合A,记作或.
特别提示
(1)符号“”“”(或“”)是表示元素与集合之间关系的,不能用来表示集合与集合之间的关系.
(2)与取决于a是不是集合A的元素.根据集合中元素的确定性,可知对任何a与A,与(或)这两种情况中必有一种且只有一种成立.
典例探究
例2 数集A满足条件:若,则(),若,求集合A中的其他元素.
思路图示
答案 ,且,
,
故集合A中的其他元素为.
方法归纳
1.求集合中的元素,就是求满足集合中元素的特征的值.
2.注意集合中元素的互异.
变式训练2 集合,集合,下列选项中元素与集合的关系都正确的是( )
A.
B.
C.
D.
答案 C
点拨 集合A中的元素y是实数,不是有序实数对,故B,D不正确;集合B中的元素是有序实数对而不是实数,所以A不正确,易知C正确.
探究点3..列举法
知识详解
1.将集合的元素一一列举出来,并置于花括号“{}”内,这种表示集合的方法叫作列举法例如,“小于10的所有自然数组成的集合”表示为.
2.一般情况下,对于有限集,在元素不太多的情况下宜采用列举法,它具有直观明了的特点.
3.用列举法表示集合时,应注意:①元素间用“,”分隔;②集合中的元素要具有确定性、互异性、无序性三个特性;③若元素个数较多或无限个且构成集合的这些元素有明显规律,在不发生误解的情况下,也可用列举法,但必须把元素规律显示清楚后才能用省略号.如不超过100的正整数构成的集合可表示为.
典例探究
例3 已知集合是小于6的正整数,是小于10的质数,是24和36的公约数,用列举法表示下列集合:
(1);
(2).
解析 要求的集合M与N中的元素与集合有关,先将集合用列举法表示,然后求解.
答案 集合.
(1),且.
(2),且.
方法归纳 解此题的关键是理解M的元素既是A的元素又是C的元素,N的元素是B的元素但不是C的元素,这体现了符号语言和文字语言的互译.
变式训练3 设a,b都是非零实数,所有可能的值组成的集合是( )
A.
B.
C.
D.
答案 D
点拨 因为的结果是1还是,取决于x的正负,所以本题应从a,b的正负来分类讨论,共有四种情况,讨论得出结果,注意集合的元素不能重复.
探究点4 描述法
知识详解
1.将集合的所有元素都具有的性质(满足的条件)表示出来,写成的形式,这样的方法称为描述法.具体方法是:在花括号内先写上表示这个集合的元素的般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征.
描述法的语言形式有三种:文字语言、符号语言、图形语言.
2.对无限集,一般采用描述法表示.它的优点是形式简洁,能充分体现集合中元素的特征.
3.使用描述法时,应注意六点:
①写清楚集合中元素的代表符号;
②说明该集合中元素的性质;
③不能出现未被说明的字母;
④多层描述时,应当准确使用“且”“或”;
⑤所有描述的内容都要写在括号内;
⑥用于描述的语句力求简明、确切.
典例探究
例4 用描述法表示下列集合:
(1);
(2);
(3)正偶数集;
(4)被3除余2的正整数组成的集合;
(5)平面直角坐标系中坐标轴上的点组成的集合;
(6).
解析 根据描述法的形式要求改写表示方法.
答案 (1)可表示为.
(2)可表示为.
(3)可表示为.
偶数用式子可表示为,但此题要求x为正偶数,故.
(4)可表示为.
设被3除余2的数为x,则,但此题要求x为正整数,故,,也可以写成,,注意此时n从1开始.
(5)可表示为.
此集合是点集,坐标轴上的点的特征是横、纵坐标中至少有一个为0,即.
(6)可表示为.
集合中各元素为正整数的平方,故各元素可表示为,也可以写成.
方法归纳 用描述法表示集合的基本步骤:(1)弄清元素的形式;(2)写出代表元素,写在“”前面;(3)确定元素所具有的属性,写在“”的后面;(4)用花括号把它们括起来.
变式训练4 把下列用描述法表示的集合用列举法表示:
(1);
(2).
答案 (1),
.
(2).
,即.
.
点拨 集合M中的代表元素是,集合N中的代表元素是,而不是x,同时要注意(1)中,,(2)中等约束条件.
易错易混解读
例 已知集合,且,则x的值为( )
A.
B.3
C.或3
D.
错解 C
错因分析 该题易错选C,原因是忽略了检验集合元素的互异性,导致多选了.
正解 ,
.
当时,,不满足互异性,故;
当时,解得(舍去),当时,集合,符合题意,.
答案 A
纠错心得 当集合中的元素含有字母时,求出参数后,一定要代回检验,确保满足集合元素的互异性.
课堂快速检测
一、选择题
1.下列各组对象能构成集合的有( )
①接近于0的实数;②小于0的实数;③与;④1,2,3.
A.1组
B.2组
C.3组
D.4
2.下列集合中与是同一集合的是( )
A.
B.
C.
D.
3.已知,且,则a的值为( )
A.0
B.1
C.2
D.3
4.已知集合中的三个元素是的三边长,那么一定不是( )
A.锐角三角形
B直角三角形
C.钝角三角形
D.等腰三角形
5.下列集合恰有两个元素的是( )
A.
B.
C.
D.
二、解答题
6.用适当的方法表示下列集合
(1)大于小于12.8的整数的全体;
(2)梯形的全体构成的集合;
(3)所有能被3整除的数的集合;
(4)方程的解集;
(5)不等式的解集.
答案
1.
答案:C
解析:①中“接近于0”不是一个明确的标准,不满足集合中元素的确定性,所以不能构成集合;②中“小于0”是个明确的标准,能构成集合;③中与是两个不同的对象,是确定的,能构成集合,该集合有两个元素;④中的对象是确定的,可以构成集合,构成的集合为{1,2,3}.
2.
答案:D
解析:由集合中元素的无序性可知D正确.
3.
答案:D
解析:由元素与集合的关系知,.
4.
答案:D
解析:由集合中元素的互异性知互不相等,故选D.
5.
答案:C
解析:A表示只含有一个方程的集合;B表示函数中自变量的取值集合,有无数个元素;C表示方程的解集,有0,1两个元素;D表示函数的函数值的取值集合,有无数个元素.
6.
答案:见解析
解析:(1).
(2).
(3).
(4).
(5).
要点概括整合
1.本节知识导图:
2.这节课所涉及的方法有分类讨论和转化的数学思想方法.
1 / 12
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
