苏教版(2019)高中数学必修第一册 1.2《子集、全集、补集》精品课件(共18张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 1.2《子集、全集、补集》精品课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 07:24:39 | ||
图片预览






文档简介
(共18张PPT)
苏教版同步教材精品课件
1.2 子集、全集、补集
情境引入
问题:实数有相等、大小的关系,如等,类比实数之间的关系,你能猜想集合之间除了相等还有哪些关系吗?
师生互动:教师提出问题,学生回答.
设计意图:让学生根据实数的大小关系类比集合之间的关系.
探究新知
概念形成
阅读教材第9页上面的(1)(2)(3)三个例子,体会每个例子的两个集合中,前一个集合与后一个集合的元素有什么关系.
1.子集的概念.
如果集合A的任意一个元素都是集合B的元素(若,则),那么集合A称为集合B的子集,记为或,读作“集合A包含于集合B”或“集合B包含集合A”.
说明:(1)与具有同样的含义.
(2)“包含”可表达成:对任意,则.
(3)可用Venn图示法表示出两个集合的包含关系(如图所示).
(4)性质有两条:.
(5)再举例,让学生巩固对子集的理解.
师生互动:师:引导学生观察三个例子中两个集合之间元素的关系,并归纳子集的定义.
生:观察三个例子,回答教师的问题,归纳子集的定义.
设计意图:培养学生数学抽象的核心素养,强化观察能力和运用数学语言表达的能力.
探究新知
2.真子集.
如果,并且,那么集合A称为集合B的真子集,记为或,读作“A真包含于B”或“B真包含A”,如.
师生互动:师:分析真子集的含义,引导学生分析子集与真子集的区别和联系.
生:讨论发现问题.
设计意图:掌握真子集的概念,弄清子集和真子集的区别.
探究新知
3.补集的定义.
设,由S中不属于A的所有元素组成的集合称为S的子集A的补集,记为(读作“A在S中的补集”),即.图形语言如下:
师生互动:师:从例3中引导学生归纳补集的定义.
生:结合例3归纳补集的定义.
设计意图:培养归纳能力,达到数学抽象核心素养的要求.
探究新知
4.如果一个集合包含我们所研究问题中涉及的所有元素,那么就称这个集合为全集,全集通常记作U.
说明:(1)在实数范围内讨论集合时,R便可看作个全集U.(2)通常也把给定的集合作为全集,研究的对象不同,全集也就不同,全集具有相对性.
师生互动:师:给出几个不同的全集的例子,让学生体会全集的意义及全集的相对性.
生:阅读教材全集的定义,思考、讨论并回答教师提出的问题.
设计意图:理解全集的概念.
概念深化
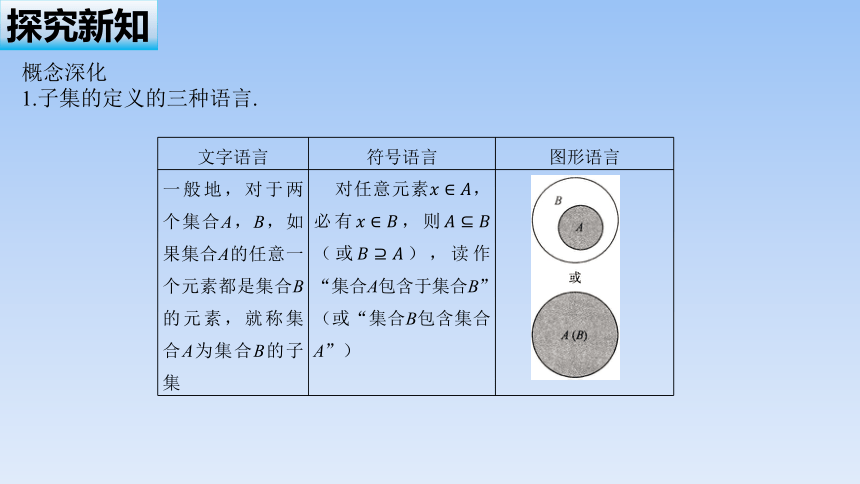
1.子集的定义的三种语言.
探究新知
文字语言 符号语言 图形语言
一般地,对于两个集合A,B,如果集合A的任意一个元素都是集合B的元素,就称集合A为集合B的子集 对任意元素,必有,则(或),读作“集合A包含于集合B”(或“集合B包含集合A”)
几点说明:
(1)“A是B的子集”的含义是:集合A中的任何个元素都是集合B的元素,即若,则由,能推出.
(2)如果集合A中存在着不是集合B的元素,那么集合A不包含于集合B,或集合B不包含集合A,集合A,B就不具有子集关系.
(3)在子集的定义中,不能理解为集合A是集合B的部分元素所组成的集合因为集合A中也可以不含任何元素,即;若,则集合A中含有集合B的所有元素,但此时我们也可以说集合A是集合B的子集,即.
师生互动:师:从不同的角度对定义提出问题.
生:结合文字语言,转换为符号和图形语言,并相互讨论.
师生共同归纳子集定义的三种语言.
设计意图:培养学生观察、分析和归纳概括问题的能力,初步理解用Venn图表示子集关系,达到培养数学抽象核心素养的要求,加深对子集的理解.
探究新知
2.真子集的理解.
探究新知
文字语言 符号语言 图形语言
如果集合A是集合B的子集,且在集合B中至少存在一个元素不是集合A的元素,我们称集合A是集合B的真子集. 如果集合,且,即存在元素,且,则(或),读作“A真包含于B”(或“B真包含A”)
几点说明:
(1)理解真子集概念时,需明确:,首先要满足,其次要满足,即至少有一个元素且.如集合,则,且集合B中有两个元素不属于集合,满足至少有一个元素不属于集合A,故.
(2)包含、真包含关系(“”与“”)是集合与集合之间的关系,是集体与集体之间的关系;属于关系()是元素与集合之间的关系,是个体与集体之间的关系.
(3)注意符号“”与“ ”的区别或.若和同时成立,则更能准确表达集合A,B之间的关系例如,若集合,,则集合A是集合B的子集,也是真子集,用与均可,但用更准确.
师生互动:师:课件出示问题,引导学生理解真子集.
生:从问题中感悟真子集的特点,回答教师提出的问题.
设计意图:加深对真子集的理解,能区分子集和真子集的关系.
探究新知
3.补集的理解.
探究新知
自然语言 对于集合A和U,若,由全集U中不属于集合A的所有元素组成的集合称为全集U的子集A的补集,记作
符号语言
图形语言
探究新知
几点说明:
(1)补集是相对于全集而言的,它与全集不可分割.一方面,若没有定义全集,则不存在补集的说法;另方面,补集的元素逃不出全集的范围.
(2)补集是集合之间的一种关系,也是一种运算求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的.
(3)集合的补集运算与实数的减法运算可进行类比:
实数 集合
被减数a 被减集合(全集)U
减数b 减集合A
差 补集
(4)符号有三层意思:①A是U的子集,即;② 表示一个集合,且;③ 是U中不属于A的所有元素组成的集合,即.
(5)若,则或,二者必居其一.
师生互动:师:出示关于补集的说明,逐条解释每条的含义,然后通过问题加深学生对说明的理解.
生:结合教师的说明,交流、探讨对补集的理解深度,回答教师的问题.
设计意图:培养学生的自学能力,加深对补集的理解,培养学生的归纳和语言概括能力,达到培养数学抽象核心素养的目的.
探究新知
典例剖析
例1、教材第9页例1.
练习:教材第11页练习第3题(1)~(3)题.
例2、教材第9页例2.
练习:教材11页练习第1题.
例3、教材第10页例3.
练习:教材第11页习题1.2第2题.
例4、教材第10页例4.
练习:教材第11页练习第4,5,6题.
典例剖析
师生互动:生:口答.
师:引导其他学生判断正误,并对错误进行改正.
生:板演,教师巡视观察指导,师生共同点评练习,总结错误的原因,并进行改正.
师:引导学生自学例2,巡回检查.
生:口答.
师生共同点评.师分析例3,并提醒注意关键点.
两生板演例4.
师:点评例4,再强调关键点,即端点的问题.
生板演,师巡回指导,纠正错误.
典例剖析
设计意图:锻炼学生的应用能力和表达能力.
通过例2总结求一个集合的子集的方法,并归纳子集的个数与原集合元素个数的关系.
通过例3为学习补集做铺垫.
培养学生学会用数轴解决补集问题,体会数轴在解决补集问题中的优越性.
课堂小结
1.知识:
(1)子集的定义;
(2)真子集的定义;
(3)补集的定义;
(4)全集的定义
2.方法:
利用Venn图表示集合和用数轴求补集的方法.
师生互动:学生相互交流收获与体会,并进行反思.
设计意图:关注学生的自主体验,提高其归纳总结能力.
作 业
1.教材第11页习题1.2第3,4,6题.
2.教材第11页习题1.2第7题(分层作业,有余力的学生做).
师生互动:学生课下独立完成,教师批阅并公布学生做题情况,有问题给予纠正.
设计意图:通过分层作业使学生巩固所学知识,为有余力的学生提供进一步学习的机会.
苏教版同步教材精品课件
1.2 子集、全集、补集
情境引入
问题:实数有相等、大小的关系,如等,类比实数之间的关系,你能猜想集合之间除了相等还有哪些关系吗?
师生互动:教师提出问题,学生回答.
设计意图:让学生根据实数的大小关系类比集合之间的关系.
探究新知
概念形成
阅读教材第9页上面的(1)(2)(3)三个例子,体会每个例子的两个集合中,前一个集合与后一个集合的元素有什么关系.
1.子集的概念.
如果集合A的任意一个元素都是集合B的元素(若,则),那么集合A称为集合B的子集,记为或,读作“集合A包含于集合B”或“集合B包含集合A”.
说明:(1)与具有同样的含义.
(2)“包含”可表达成:对任意,则.
(3)可用Venn图示法表示出两个集合的包含关系(如图所示).
(4)性质有两条:.
(5)再举例,让学生巩固对子集的理解.
师生互动:师:引导学生观察三个例子中两个集合之间元素的关系,并归纳子集的定义.
生:观察三个例子,回答教师的问题,归纳子集的定义.
设计意图:培养学生数学抽象的核心素养,强化观察能力和运用数学语言表达的能力.
探究新知
2.真子集.
如果,并且,那么集合A称为集合B的真子集,记为或,读作“A真包含于B”或“B真包含A”,如.
师生互动:师:分析真子集的含义,引导学生分析子集与真子集的区别和联系.
生:讨论发现问题.
设计意图:掌握真子集的概念,弄清子集和真子集的区别.
探究新知
3.补集的定义.
设,由S中不属于A的所有元素组成的集合称为S的子集A的补集,记为(读作“A在S中的补集”),即.图形语言如下:
师生互动:师:从例3中引导学生归纳补集的定义.
生:结合例3归纳补集的定义.
设计意图:培养归纳能力,达到数学抽象核心素养的要求.
探究新知
4.如果一个集合包含我们所研究问题中涉及的所有元素,那么就称这个集合为全集,全集通常记作U.
说明:(1)在实数范围内讨论集合时,R便可看作个全集U.(2)通常也把给定的集合作为全集,研究的对象不同,全集也就不同,全集具有相对性.
师生互动:师:给出几个不同的全集的例子,让学生体会全集的意义及全集的相对性.
生:阅读教材全集的定义,思考、讨论并回答教师提出的问题.
设计意图:理解全集的概念.
概念深化
1.子集的定义的三种语言.
探究新知
文字语言 符号语言 图形语言
一般地,对于两个集合A,B,如果集合A的任意一个元素都是集合B的元素,就称集合A为集合B的子集 对任意元素,必有,则(或),读作“集合A包含于集合B”(或“集合B包含集合A”)
几点说明:
(1)“A是B的子集”的含义是:集合A中的任何个元素都是集合B的元素,即若,则由,能推出.
(2)如果集合A中存在着不是集合B的元素,那么集合A不包含于集合B,或集合B不包含集合A,集合A,B就不具有子集关系.
(3)在子集的定义中,不能理解为集合A是集合B的部分元素所组成的集合因为集合A中也可以不含任何元素,即;若,则集合A中含有集合B的所有元素,但此时我们也可以说集合A是集合B的子集,即.
师生互动:师:从不同的角度对定义提出问题.
生:结合文字语言,转换为符号和图形语言,并相互讨论.
师生共同归纳子集定义的三种语言.
设计意图:培养学生观察、分析和归纳概括问题的能力,初步理解用Venn图表示子集关系,达到培养数学抽象核心素养的要求,加深对子集的理解.
探究新知
2.真子集的理解.
探究新知
文字语言 符号语言 图形语言
如果集合A是集合B的子集,且在集合B中至少存在一个元素不是集合A的元素,我们称集合A是集合B的真子集. 如果集合,且,即存在元素,且,则(或),读作“A真包含于B”(或“B真包含A”)
几点说明:
(1)理解真子集概念时,需明确:,首先要满足,其次要满足,即至少有一个元素且.如集合,则,且集合B中有两个元素不属于集合,满足至少有一个元素不属于集合A,故.
(2)包含、真包含关系(“”与“”)是集合与集合之间的关系,是集体与集体之间的关系;属于关系()是元素与集合之间的关系,是个体与集体之间的关系.
(3)注意符号“”与“ ”的区别或.若和同时成立,则更能准确表达集合A,B之间的关系例如,若集合,,则集合A是集合B的子集,也是真子集,用与均可,但用更准确.
师生互动:师:课件出示问题,引导学生理解真子集.
生:从问题中感悟真子集的特点,回答教师提出的问题.
设计意图:加深对真子集的理解,能区分子集和真子集的关系.
探究新知
3.补集的理解.
探究新知
自然语言 对于集合A和U,若,由全集U中不属于集合A的所有元素组成的集合称为全集U的子集A的补集,记作
符号语言
图形语言
探究新知
几点说明:
(1)补集是相对于全集而言的,它与全集不可分割.一方面,若没有定义全集,则不存在补集的说法;另方面,补集的元素逃不出全集的范围.
(2)补集是集合之间的一种关系,也是一种运算求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的.
(3)集合的补集运算与实数的减法运算可进行类比:
实数 集合
被减数a 被减集合(全集)U
减数b 减集合A
差 补集
(4)符号有三层意思:①A是U的子集,即;② 表示一个集合,且;③ 是U中不属于A的所有元素组成的集合,即.
(5)若,则或,二者必居其一.
师生互动:师:出示关于补集的说明,逐条解释每条的含义,然后通过问题加深学生对说明的理解.
生:结合教师的说明,交流、探讨对补集的理解深度,回答教师的问题.
设计意图:培养学生的自学能力,加深对补集的理解,培养学生的归纳和语言概括能力,达到培养数学抽象核心素养的目的.
探究新知
典例剖析
例1、教材第9页例1.
练习:教材第11页练习第3题(1)~(3)题.
例2、教材第9页例2.
练习:教材11页练习第1题.
例3、教材第10页例3.
练习:教材第11页习题1.2第2题.
例4、教材第10页例4.
练习:教材第11页练习第4,5,6题.
典例剖析
师生互动:生:口答.
师:引导其他学生判断正误,并对错误进行改正.
生:板演,教师巡视观察指导,师生共同点评练习,总结错误的原因,并进行改正.
师:引导学生自学例2,巡回检查.
生:口答.
师生共同点评.师分析例3,并提醒注意关键点.
两生板演例4.
师:点评例4,再强调关键点,即端点的问题.
生板演,师巡回指导,纠正错误.
典例剖析
设计意图:锻炼学生的应用能力和表达能力.
通过例2总结求一个集合的子集的方法,并归纳子集的个数与原集合元素个数的关系.
通过例3为学习补集做铺垫.
培养学生学会用数轴解决补集问题,体会数轴在解决补集问题中的优越性.
课堂小结
1.知识:
(1)子集的定义;
(2)真子集的定义;
(3)补集的定义;
(4)全集的定义
2.方法:
利用Venn图表示集合和用数轴求补集的方法.
师生互动:学生相互交流收获与体会,并进行反思.
设计意图:关注学生的自主体验,提高其归纳总结能力.
作 业
1.教材第11页习题1.2第3,4,6题.
2.教材第11页习题1.2第7题(分层作业,有余力的学生做).
师生互动:学生课下独立完成,教师批阅并公布学生做题情况,有问题给予纠正.
设计意图:通过分层作业使学生巩固所学知识,为有余力的学生提供进一步学习的机会.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
