省级教学竞赛获奖课件3.1.2函数的表示(第一课时) 课件(共26张PPT)
文档属性
| 名称 | 省级教学竞赛获奖课件3.1.2函数的表示(第一课时) 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 644.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 08:59:59 | ||
图片预览







文档简介
(共26张PPT)
第三章 函数的概念与性质
3.1.2 函数的表示(第一课时)
教学目标
明确函数的三种表示方法(重点)
01
在实际情景中,能根据不同的条件选择适当的方法表示函数(重点、难点)
02
了解构成函数的要素,会求一一些简单函数的定义域和值域(重点)
03
能够正确使用区间表示数集
04
函数的表示
学科素养
函数的概念
数学抽象
直观想象
f (x)与f (a)的关系
逻辑推理
函数定义域的求解
数学运算
数据分析
数学建模
函数的表示
01
知 识 回 顾
Retrospective Knowledge
函数的表示
构成函数的三要素: 定义域,对应关系和值域.
回想我们在初中已经接触过的函数的表示方法有哪几种?
解析法 列表法 图象法
列出表格来表示两个变量之间的对应关系
用图象表示两个变量之间的对应关系
用数学表达式表示两个变量之间的对应关系
02
新 知 探 索
New Knowledge explore
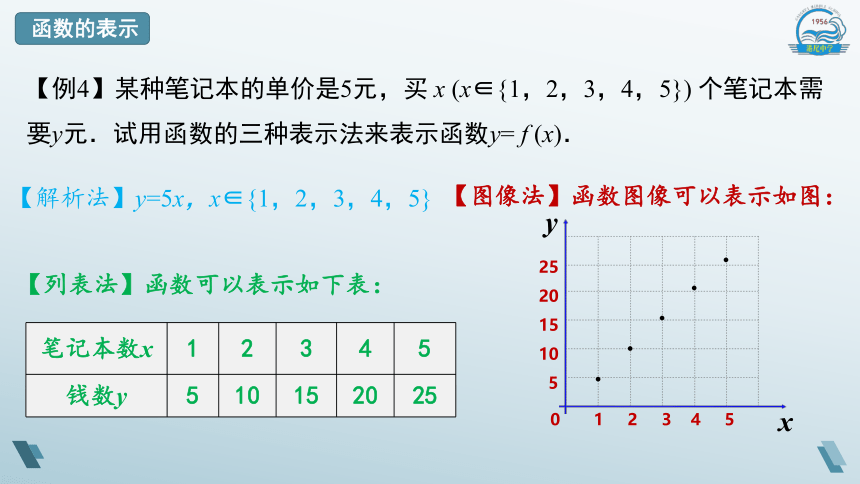
【例4】某种笔记本的单价是5元,买 x (x∈{1,2,3,4,5}) 个笔记本需要y元.试用函数的三种表示法来表示函数y= f (x).
【列表法】函数可以表示如下表:
【解析法】y=5x,x∈{1,2,3,4,5}
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
【图像法】函数图像可以表示如图:
25
20
15
10
5
0 1 2 3 4 5
x
y
【1】解析法必须标明函数的定义域;
在用三种方法表示函数时要注意
【2】列表法必须罗列出所有的自变量与函数值之间的对应关系;
【3】图像法必须搞清楚函数图像是“点”还是“线”.
(1)比较函数的三种表示法,它们各有什么特点?
(2)所有函数都能用解析法吗?列表法与图像法呢?请举出实例加以说明?
解析法:对应关系清楚、简明、全面;
通过解析式可求出任意自变量对应的函数值,便于研究函数性质.
列表法:不用计算,看表就知道函数值;
但当自变量较多时,列表不易实现.
图像法:形象、直观地表示出函数的变化情况;
但求函数值比较困难,只能求近似值,且误差较大.
(1)比较函数的三种表示法,它们各有什么特点?
(2)所有函数都能用解析法吗?列表法与图像法呢?请举出实例加以说明?
【例7】下表是某校高一(1)班3名同学在高一学年度6次数学测试的成绩及班级平均分表.请你对这三位同学在初三学年的历史学习情况做一个分析.
【分析】从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将每位同学的成绩和测试序号之间的函数关系分别用图像表示出来,就可以直观的看到他们成绩变化的情况.
【分析】从图像中我们可以直观地看到:王伟同学的成绩一直稳定在班级的前茅, 张城同学的成绩波动较大,赵磊同学的成绩整体有下降趋势,但三位同学的成绩基本上都大幅领先于班级平均水平.
【练习3】 如左下图所示,水从一圆锥形漏斗漏入圆柱形桶中,H是圆锥形漏斗中水面下降的距离,则H与下降时间t(分钟)的函数关系用图象表示只可能是 ( )
B
03
拓 展 提 升
Expansion And Promotion
例1.已知f(x)=x2 +x -1,则f(x+1)=________.
解析式的求法 - 代入法
题型一. 由f(x)的解析式求f[g(x)]的解析式.
代入法:已知f (x)求f (g(x)),只需把f (x)中的x用g(x)代入即可.
例2.已知f (x)=2x +1,则 f(f (x))=________.
解析式的求法 - 代入法
题型一. 由f(x)的解析式求f[g(x)]的解析式.
代入法:已知f (x)求f (g(x)),只需把f (x)中的x用g(x)代入即可.
解析式的求法 - 配凑法
题型二. 由f[g(x)]的解析式求f(x)的解析式.
例3.已知f(x+1)=x2+3x+1,则f(x)=________.
例1的 逆运算
配凑法:已知f (g(x))=h(x),求f (x)的问题,往往把右边的h(x)整理或配凑成
只含g(x)的式子, 再用x将g(x)替换即可得f (x).
题型二. 由f[g(x)]的解析式求f(x)的解析式.
解析式的求法 - 换元法
换元法:已知f(g(x))=h(x),求f(x)时,往往可设g(x)=t,从中解出x,代入h(x)
进行换元,便可求得f (t),再把t用x替换即可得f (x).
解析式的求法 - 待定系数法
题型三. 已知函数f(x)的类型,求f(x)的解析式.
例5.已知f(x)是一次函数,且f(f(x))=4x -1,则f(x)=________.
待定系数法:已知函数f (x)的类型(如一次函数、二次函数),可设函数f (x)的
解析式,根据条件求出其中的系数,再代回解析式即可得f (x).
解析式的求法 - 待定系数法
题型三. 已知函数f(x)的类型,求f(x)的解析式.
待定系数法:已知函数f(x)的类型(如一次函数、二次函数),可设函数f(x)的
解析式,根据条件求出其中的系数,再代回解析式即可得f(x).
另解:配凑法
换元法
04
归 纳 总 结
Sum Up
函数的三种表示:
解析法:对应关系清楚、简明、全面;
通过解析式可求出任意自变量对应的函数值,便于研究函数性质.
列表法:不用计算,看表就知道函数值;
但当自变量较多时,列表不易实现.
图像法:形象、直观地表示出函数的变化情况;
但求函数值比较困难,只能求近似值,且误差较大.
求函数解析式的常用方法
代入法:已知f (x)求f(g(x)),只需把f (x)中的x用g(x)代入即可;
配凑法:已知f (g(x))=h(x),求f (x)的问题,往往把右边的h(x)整理或配凑成只
含g(x)的式子, 再用x将g(x)替换即可得f(x);
换元法:已知f(g(x))=h(x),求f (x)时,往往可设g(x)=t,从中解出x,代入h(x) 进行
换元,便可求得f (t),再把t用x替换即可得f (x);
待定系数法:已知函数f (x)的类型(如一次函数、二次函数),可设函数f (x)的
解析式,根据条件求出其中的系数,再代回解析式即可得f (x);
05
课 后 作 业
Homework After Class
第三章 函数的概念与性质
3.1.2 函数的表示(第一课时)
教学目标
明确函数的三种表示方法(重点)
01
在实际情景中,能根据不同的条件选择适当的方法表示函数(重点、难点)
02
了解构成函数的要素,会求一一些简单函数的定义域和值域(重点)
03
能够正确使用区间表示数集
04
函数的表示
学科素养
函数的概念
数学抽象
直观想象
f (x)与f (a)的关系
逻辑推理
函数定义域的求解
数学运算
数据分析
数学建模
函数的表示
01
知 识 回 顾
Retrospective Knowledge
函数的表示
构成函数的三要素: 定义域,对应关系和值域.
回想我们在初中已经接触过的函数的表示方法有哪几种?
解析法 列表法 图象法
列出表格来表示两个变量之间的对应关系
用图象表示两个变量之间的对应关系
用数学表达式表示两个变量之间的对应关系
02
新 知 探 索
New Knowledge explore
【例4】某种笔记本的单价是5元,买 x (x∈{1,2,3,4,5}) 个笔记本需要y元.试用函数的三种表示法来表示函数y= f (x).
【列表法】函数可以表示如下表:
【解析法】y=5x,x∈{1,2,3,4,5}
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
【图像法】函数图像可以表示如图:
25
20
15
10
5
0 1 2 3 4 5
x
y
【1】解析法必须标明函数的定义域;
在用三种方法表示函数时要注意
【2】列表法必须罗列出所有的自变量与函数值之间的对应关系;
【3】图像法必须搞清楚函数图像是“点”还是“线”.
(1)比较函数的三种表示法,它们各有什么特点?
(2)所有函数都能用解析法吗?列表法与图像法呢?请举出实例加以说明?
解析法:对应关系清楚、简明、全面;
通过解析式可求出任意自变量对应的函数值,便于研究函数性质.
列表法:不用计算,看表就知道函数值;
但当自变量较多时,列表不易实现.
图像法:形象、直观地表示出函数的变化情况;
但求函数值比较困难,只能求近似值,且误差较大.
(1)比较函数的三种表示法,它们各有什么特点?
(2)所有函数都能用解析法吗?列表法与图像法呢?请举出实例加以说明?
【例7】下表是某校高一(1)班3名同学在高一学年度6次数学测试的成绩及班级平均分表.请你对这三位同学在初三学年的历史学习情况做一个分析.
【分析】从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将每位同学的成绩和测试序号之间的函数关系分别用图像表示出来,就可以直观的看到他们成绩变化的情况.
【分析】从图像中我们可以直观地看到:王伟同学的成绩一直稳定在班级的前茅, 张城同学的成绩波动较大,赵磊同学的成绩整体有下降趋势,但三位同学的成绩基本上都大幅领先于班级平均水平.
【练习3】 如左下图所示,水从一圆锥形漏斗漏入圆柱形桶中,H是圆锥形漏斗中水面下降的距离,则H与下降时间t(分钟)的函数关系用图象表示只可能是 ( )
B
03
拓 展 提 升
Expansion And Promotion
例1.已知f(x)=x2 +x -1,则f(x+1)=________.
解析式的求法 - 代入法
题型一. 由f(x)的解析式求f[g(x)]的解析式.
代入法:已知f (x)求f (g(x)),只需把f (x)中的x用g(x)代入即可.
例2.已知f (x)=2x +1,则 f(f (x))=________.
解析式的求法 - 代入法
题型一. 由f(x)的解析式求f[g(x)]的解析式.
代入法:已知f (x)求f (g(x)),只需把f (x)中的x用g(x)代入即可.
解析式的求法 - 配凑法
题型二. 由f[g(x)]的解析式求f(x)的解析式.
例3.已知f(x+1)=x2+3x+1,则f(x)=________.
例1的 逆运算
配凑法:已知f (g(x))=h(x),求f (x)的问题,往往把右边的h(x)整理或配凑成
只含g(x)的式子, 再用x将g(x)替换即可得f (x).
题型二. 由f[g(x)]的解析式求f(x)的解析式.
解析式的求法 - 换元法
换元法:已知f(g(x))=h(x),求f(x)时,往往可设g(x)=t,从中解出x,代入h(x)
进行换元,便可求得f (t),再把t用x替换即可得f (x).
解析式的求法 - 待定系数法
题型三. 已知函数f(x)的类型,求f(x)的解析式.
例5.已知f(x)是一次函数,且f(f(x))=4x -1,则f(x)=________.
待定系数法:已知函数f (x)的类型(如一次函数、二次函数),可设函数f (x)的
解析式,根据条件求出其中的系数,再代回解析式即可得f (x).
解析式的求法 - 待定系数法
题型三. 已知函数f(x)的类型,求f(x)的解析式.
待定系数法:已知函数f(x)的类型(如一次函数、二次函数),可设函数f(x)的
解析式,根据条件求出其中的系数,再代回解析式即可得f(x).
另解:配凑法
换元法
04
归 纳 总 结
Sum Up
函数的三种表示:
解析法:对应关系清楚、简明、全面;
通过解析式可求出任意自变量对应的函数值,便于研究函数性质.
列表法:不用计算,看表就知道函数值;
但当自变量较多时,列表不易实现.
图像法:形象、直观地表示出函数的变化情况;
但求函数值比较困难,只能求近似值,且误差较大.
求函数解析式的常用方法
代入法:已知f (x)求f(g(x)),只需把f (x)中的x用g(x)代入即可;
配凑法:已知f (g(x))=h(x),求f (x)的问题,往往把右边的h(x)整理或配凑成只
含g(x)的式子, 再用x将g(x)替换即可得f(x);
换元法:已知f(g(x))=h(x),求f (x)时,往往可设g(x)=t,从中解出x,代入h(x) 进行
换元,便可求得f (t),再把t用x替换即可得f (x);
待定系数法:已知函数f (x)的类型(如一次函数、二次函数),可设函数f (x)的
解析式,根据条件求出其中的系数,再代回解析式即可得f (x);
05
课 后 作 业
Homework After Class
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
