省级教学竞赛获奖课件4.2.2指数函数的图象和性质 课件(共30张PPT)
文档属性
| 名称 | 省级教学竞赛获奖课件4.2.2指数函数的图象和性质 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 600.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 09:09:20 | ||
图片预览








文档简介
(共30张PPT)
第四章 指数函数与对数函数
4.2.2 指数函数的图象和性质
教学目标
能画出具体指数函数的图象(重点)
01
掌握指数函数的性质,能应用解决简单的问题(重点、难点)
02
03
04
指数函数的图象和性质
学科素养
指数函数的性质
数学抽象
指数函数图像
直观想象
类比法学习指数函数性质
逻辑推理
运用指数函数性质解决问题
数学运算
利用指数函数的性质比较两个函数值的大小
数据分析
在实际问题中建立指数函数模型
数学建模
指数函数的图象和性质
01
知 识 回 顾
Retrospective Knowledge
指数函数的概念
指数函数的概念:
一般地,形如y=ax(a>0,且a≠1)的函数叫做指数函数,其中指数x是自变量,定义域为R.
解析式特点:
【1】ax的系数为1;
【2】ax的指数为自变量;
【3】ax的底数是大于零且不等于1的常数.
02
新 知 探 索
New Knowledge explore
研究函数的一般方法:
背景
概念
图像与性质
应用
为了研究指数函数,下面我们类比研究幂函数性质的过程和方法,首先作出指数函数的图像,然后借助指数函数的图像研究指数函数的性质.
x y
-2
-1.5 0.35
-1
-0.5 0.71
0
0.5 1.41
1
1.5 2.83
2
0.25
0.5
1
2
4
1
x
y
o
1
2
3
-1
-2
-3
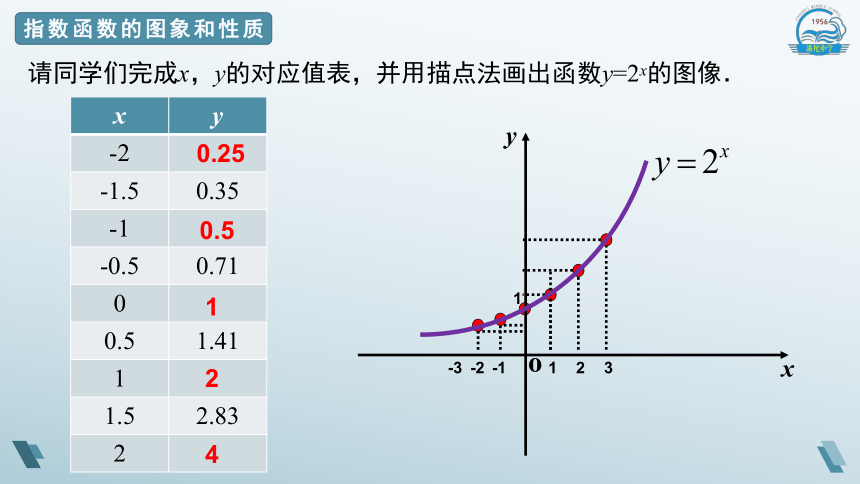
请同学们完成x,y的对应值表,并用描点法画出函数y=2x的图像.
x y
-2 0.25
-1.5 0.35
-1 0.5
-0.5 0.71
0 1
0.5 1.41
1 2
1.5 2.83
2 4
x y
-2
-1.5 2.83
-1
-0.5 1.41
0
0.5 0.71
1
1.5 0.35
2
4
2
1
0.5
0.25
1
x
y
o
1
2
3
-1
-2
-3
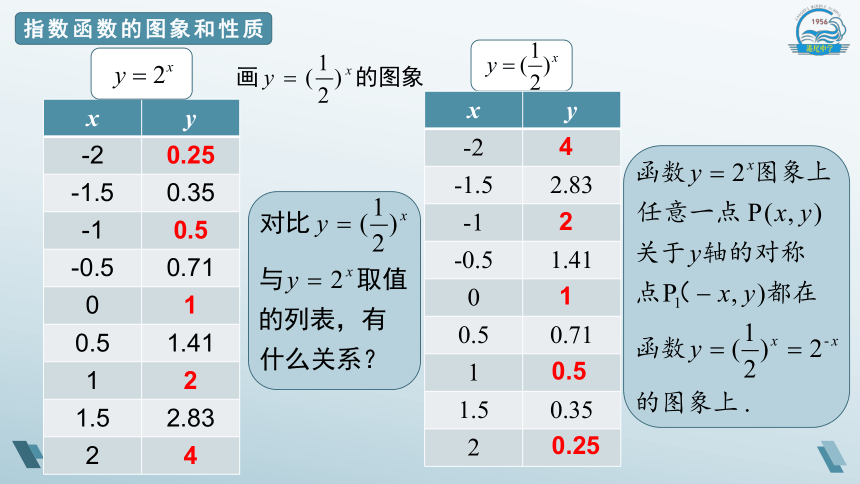
选取底数a (a>0且a≠1)的若干个不同的值,在同一直角坐标系内画出相应的指数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出指数函数y=ax (a>0且a≠1)的值域和性质吗?
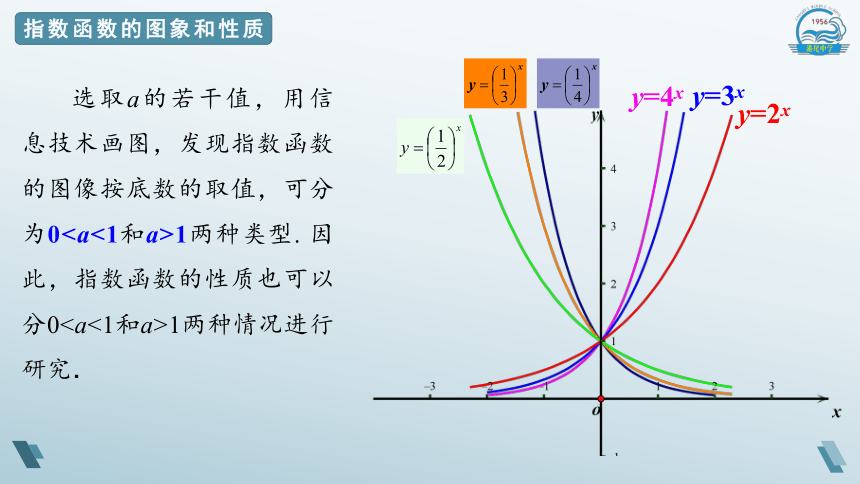
选取a的若干值,用信息技术画图,发现指数函数的图像按底数的取值,可分为01两种类型. 因此,指数函数的性质也可以分01两种情况进行
研究.
y=2x
y=3x
y=4x
a>1 0图像
定义域 值 域 过定点 性质 单调性
取 值 分 布
奇偶性
x
y
o
1
x
y
o
1
R
(0,+∞)
(0,1)
在R上是增函数
在R上是减函数
当x<0时,00时,y>1.
当x<0时,y>1;当x>0时,0既不是奇函数也不是偶函数
指数函数y=ax的图像和性质
练习1 右图是指数函数:
① y=ax,② y=bx, ③y=cx, ④ y=d x 的图象,
则a,b,c,d与1的大小关系是 ( )
A.aC.1【解析】画出直线x=1与四个指数函数的交点从下往上依次为(1,b),(1,a),(1,d),(1,c),所以有0函数y=ax在y轴右侧的图像,底数越大,图像越高(底大图高).
练习2 函数y=ax-1-2 (a>0且a≠1)的图像必过定点: .
因为函数y = ax 的图象恒过点(0,1),
所以对于函数f (x)=kag(x)+b (k,a,b均为常数,且k≠0,a>0且a≠1),
若g(m)=0,则f (x)的图象过定点(m,k+b).
解:令x-1=0,得x = 1,
所以当x=1时,y=a0-2=-1,
所以函数y=ax-1-2 (a>0且a≠1)的图像必过定点(1,-1).
例3 比较下列各题中两个值的大小:
03
拓 展 提 升
Expansion And Promotion
例 比较下列各题中两个值的大小:
比较大小
比较幂值大小的常用方法
①指数相同,构造幂函数的单调性比较大小;
②底数相同,构造指数函数的单调性比较大小;
③底数、指数都不相同
(1)可以化为同底数或同指数,那就应用方案①②;
(2)不能化为同底数或同指数,考虑寻找中间量如0或1,再进行比较.
比较大小
例 解下列不等式:
解不等式
利用指数函数的单调性解不等式
(1)利用指数型函数的单调性解不等式,需将不等式两边都凑成底数相同
的指数式.
(2)解不等式 的依据是指数型函数的单调性,要养成判断底数取值范围的习惯,若底数不确定,就需进行分类讨论.
若 则 :
当a>1时,有f (x)>g(x) ;
当0解不等式
例 求函数 的值域.
求值域
例 求函数 的值域.
求值域
函数 y = a f (x) (a>0且a≠1) 的值域的求法
①换元:令t=f(x);
②求出新元的取值范围,即求t=f(x)的值域t∈M;
③利用y=at的单调性求y=at (t∈M)的值域.
求值域
[变式]求函数 的值域.
求值域
04
归 纳 总 结
Sum Up
1. 指数函数概念:形如y = ax(a 0,且a 1)的函数叫做指数函数.
2. 指数函数的图像与性质:
3. 指数函数性质的应用
(1)比较大小:
同底构造指数函数,同指构造幂函数,利用函数的单调性比较大小;
底不同指不同利用中间值.
(2)解指数型不等式:
化同底,利用单调性确定指数的大小.
(3)求指数型函数的值域:
利用指数函数的单调性求值域;
换元转化为求二次函数的值域.
05
课 后 作 业
Homework After Class
2. 比较下列各题中两个值的大小:
1. 函数y=a2x-1+1 (a>0且a≠1)的图像必过定点: .
第四章 指数函数与对数函数
4.2.2 指数函数的图象和性质
教学目标
能画出具体指数函数的图象(重点)
01
掌握指数函数的性质,能应用解决简单的问题(重点、难点)
02
03
04
指数函数的图象和性质
学科素养
指数函数的性质
数学抽象
指数函数图像
直观想象
类比法学习指数函数性质
逻辑推理
运用指数函数性质解决问题
数学运算
利用指数函数的性质比较两个函数值的大小
数据分析
在实际问题中建立指数函数模型
数学建模
指数函数的图象和性质
01
知 识 回 顾
Retrospective Knowledge
指数函数的概念
指数函数的概念:
一般地,形如y=ax(a>0,且a≠1)的函数叫做指数函数,其中指数x是自变量,定义域为R.
解析式特点:
【1】ax的系数为1;
【2】ax的指数为自变量;
【3】ax的底数是大于零且不等于1的常数.
02
新 知 探 索
New Knowledge explore
研究函数的一般方法:
背景
概念
图像与性质
应用
为了研究指数函数,下面我们类比研究幂函数性质的过程和方法,首先作出指数函数的图像,然后借助指数函数的图像研究指数函数的性质.
x y
-2
-1.5 0.35
-1
-0.5 0.71
0
0.5 1.41
1
1.5 2.83
2
0.25
0.5
1
2
4
1
x
y
o
1
2
3
-1
-2
-3
请同学们完成x,y的对应值表,并用描点法画出函数y=2x的图像.
x y
-2 0.25
-1.5 0.35
-1 0.5
-0.5 0.71
0 1
0.5 1.41
1 2
1.5 2.83
2 4
x y
-2
-1.5 2.83
-1
-0.5 1.41
0
0.5 0.71
1
1.5 0.35
2
4
2
1
0.5
0.25
1
x
y
o
1
2
3
-1
-2
-3
选取底数a (a>0且a≠1)的若干个不同的值,在同一直角坐标系内画出相应的指数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出指数函数y=ax (a>0且a≠1)的值域和性质吗?
选取a的若干值,用信息技术画图,发现指数函数的图像按底数的取值,可分为0
研究.
y=2x
y=3x
y=4x
a>1 0
定义域 值 域 过定点 性质 单调性
取 值 分 布
奇偶性
x
y
o
1
x
y
o
1
R
(0,+∞)
(0,1)
在R上是增函数
在R上是减函数
当x<0时,0
当x<0时,y>1;当x>0时,0
指数函数y=ax的图像和性质
练习1 右图是指数函数:
① y=ax,② y=bx, ③y=cx, ④ y=d x 的图象,
则a,b,c,d与1的大小关系是 ( )
A.a
练习2 函数y=ax-1-2 (a>0且a≠1)的图像必过定点: .
因为函数y = ax 的图象恒过点(0,1),
所以对于函数f (x)=kag(x)+b (k,a,b均为常数,且k≠0,a>0且a≠1),
若g(m)=0,则f (x)的图象过定点(m,k+b).
解:令x-1=0,得x = 1,
所以当x=1时,y=a0-2=-1,
所以函数y=ax-1-2 (a>0且a≠1)的图像必过定点(1,-1).
例3 比较下列各题中两个值的大小:
03
拓 展 提 升
Expansion And Promotion
例 比较下列各题中两个值的大小:
比较大小
比较幂值大小的常用方法
①指数相同,构造幂函数的单调性比较大小;
②底数相同,构造指数函数的单调性比较大小;
③底数、指数都不相同
(1)可以化为同底数或同指数,那就应用方案①②;
(2)不能化为同底数或同指数,考虑寻找中间量如0或1,再进行比较.
比较大小
例 解下列不等式:
解不等式
利用指数函数的单调性解不等式
(1)利用指数型函数的单调性解不等式,需将不等式两边都凑成底数相同
的指数式.
(2)解不等式 的依据是指数型函数的单调性,要养成判断底数取值范围的习惯,若底数不确定,就需进行分类讨论.
若 则 :
当a>1时,有f (x)>g(x) ;
当0
例 求函数 的值域.
求值域
例 求函数 的值域.
求值域
函数 y = a f (x) (a>0且a≠1) 的值域的求法
①换元:令t=f(x);
②求出新元的取值范围,即求t=f(x)的值域t∈M;
③利用y=at的单调性求y=at (t∈M)的值域.
求值域
[变式]求函数 的值域.
求值域
04
归 纳 总 结
Sum Up
1. 指数函数概念:形如y = ax(a 0,且a 1)的函数叫做指数函数.
2. 指数函数的图像与性质:
3. 指数函数性质的应用
(1)比较大小:
同底构造指数函数,同指构造幂函数,利用函数的单调性比较大小;
底不同指不同利用中间值.
(2)解指数型不等式:
化同底,利用单调性确定指数的大小.
(3)求指数型函数的值域:
利用指数函数的单调性求值域;
换元转化为求二次函数的值域.
05
课 后 作 业
Homework After Class
2. 比较下列各题中两个值的大小:
1. 函数y=a2x-1+1 (a>0且a≠1)的图像必过定点: .
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
