省级教学竞赛获奖课件4.3.1对数的概念 课件(共30张PPT)
文档属性
| 名称 | 省级教学竞赛获奖课件4.3.1对数的概念 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 337.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 09:09:58 | ||
图片预览








文档简介
(共20张PPT)
第四章 指数函数与对数函数
4.3.1 对数的概念
教学目标
理解对数的概念,了解对数与指数的关系(重点)
01
理解和掌握对数的性质(难点)
02
掌握对数式与指数式的关系 ,学会对数式与指数式的互化(重点、难点)
03
04
对数的概念
学科素养
对数的概念
数学抽象
直观想象
对数的性质
逻辑推理
对数式与指数式的互化
数学运算
数据分析
数学建模
对数的概念
01
知 识 回 顾
Retrospective Knowledge
02
新 知 探 索
New Knowledge explore
在4.2.1的问题1中,通过指数幂运算,我们能从y=1.11x 中求出经过x年后B地景区的游客人次为2001年的y倍.
反之,如果要求经过多少年游客人次是2001年的2倍,3倍,4倍,…,那么该如何解决?
上述问题实际上就是从2=1.11x ,3=1.11x ,4=1.11x ,…中分别求出x,即已知底数和幂的值,求指数.这就是本节要学习的对数.
例如:
由于2=1.11x,所以x就是以1.11为底2的对数,记作x=log1.112;
由于3=1.11x,所以x就是以1.11为底3的对数,记作x=log1.113;
再如:
由于42=16,所以以4为底16的对数是2,记作x=log416.
一般地,如果ax=N,(a>0且a≠1),则数x叫做以a为底N的对数记作x=logaN,其中a叫底数,N叫真数.
特别注意::logaN是一个数,是一种取对数的运算,结果仍是一个数,不可分开书写.
通常,将以10为底的对数叫做常用对数,并把log10N记为lgN;另外,在科技、经济以及社会生活中经常使用以无理数e=2.71828…为底数的对数称为自然对数,并把logeN简记为lnN .
一般地,如果ax=N,(a>0且a≠1),则数x叫做以a为底N的对数记作x=logaN,其中a叫底数,N叫真数.
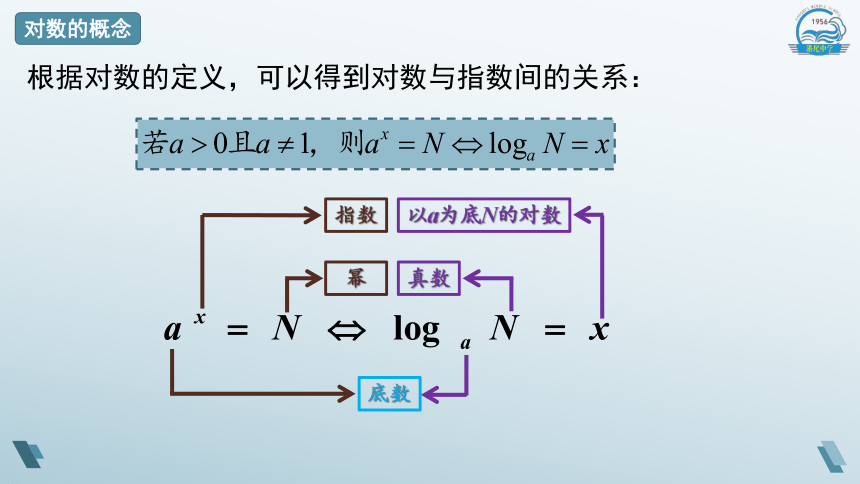
根据对数的定义,可以得到对数与指数间的关系:
底数
幂
真数
指数
以a为底N的对数
其实指数式与对数式,虽然从形式上看,两者不同,但本质上是一致的.这个一致就是底数、指数(对数)、幂(真数)三者之间的关系.
例1 将下列指数形式化为对数形式, 对数形式化为指数形式:
(1) 54=625; (2) ; (3) =5.73;
(4)log0.516=-4; (5)lg0.01=-2; (6)ln10=2.303.
根据对数的定义,可以得到对数与指数间的关系:
由指数和对数的这个关系,可以得到关于对数的如下结论:
(真数一定为正数)
利用对数与指数间的关系证明这两个结论.
因为ax=N,(a>0且a≠1),由指数函数的性质可知:N>0,所以负数和
0没有对数. (真数N一定为正数)
(1) log 64 x= ; (2) logx8=6;
(3) lg100=x; (4) -ln e2 =x.
例2 求下列各式中的x 的值:
03
拓 展 提 升
Expansion And Promotion
练习1 求下列各式的值:
(1) ; (2) .
练习2 求下列各式中的x 的值:
(1) lg(ln x)=0 ; (2) lg(ln x)=1 ; (3) log7[log3(log2x)]=0 .
04
归 纳 总 结
Sum Up
1. 对数的概念:
一般地,如果ax=N,(a>0且a≠1),则数x叫做以a为底N的对数记作x=logaN,其中a叫底数,N叫真数. (真数一定为正数)
2. 对数的性质:
05
课 后 作 业
Homework After Class
课本126页 习题4.3 第1题
求下列各式中x的值
第四章 指数函数与对数函数
4.3.1 对数的概念
教学目标
理解对数的概念,了解对数与指数的关系(重点)
01
理解和掌握对数的性质(难点)
02
掌握对数式与指数式的关系 ,学会对数式与指数式的互化(重点、难点)
03
04
对数的概念
学科素养
对数的概念
数学抽象
直观想象
对数的性质
逻辑推理
对数式与指数式的互化
数学运算
数据分析
数学建模
对数的概念
01
知 识 回 顾
Retrospective Knowledge
02
新 知 探 索
New Knowledge explore
在4.2.1的问题1中,通过指数幂运算,我们能从y=1.11x 中求出经过x年后B地景区的游客人次为2001年的y倍.
反之,如果要求经过多少年游客人次是2001年的2倍,3倍,4倍,…,那么该如何解决?
上述问题实际上就是从2=1.11x ,3=1.11x ,4=1.11x ,…中分别求出x,即已知底数和幂的值,求指数.这就是本节要学习的对数.
例如:
由于2=1.11x,所以x就是以1.11为底2的对数,记作x=log1.112;
由于3=1.11x,所以x就是以1.11为底3的对数,记作x=log1.113;
再如:
由于42=16,所以以4为底16的对数是2,记作x=log416.
一般地,如果ax=N,(a>0且a≠1),则数x叫做以a为底N的对数记作x=logaN,其中a叫底数,N叫真数.
特别注意::logaN是一个数,是一种取对数的运算,结果仍是一个数,不可分开书写.
通常,将以10为底的对数叫做常用对数,并把log10N记为lgN;另外,在科技、经济以及社会生活中经常使用以无理数e=2.71828…为底数的对数称为自然对数,并把logeN简记为lnN .
一般地,如果ax=N,(a>0且a≠1),则数x叫做以a为底N的对数记作x=logaN,其中a叫底数,N叫真数.
根据对数的定义,可以得到对数与指数间的关系:
底数
幂
真数
指数
以a为底N的对数
其实指数式与对数式,虽然从形式上看,两者不同,但本质上是一致的.这个一致就是底数、指数(对数)、幂(真数)三者之间的关系.
例1 将下列指数形式化为对数形式, 对数形式化为指数形式:
(1) 54=625; (2) ; (3) =5.73;
(4)log0.516=-4; (5)lg0.01=-2; (6)ln10=2.303.
根据对数的定义,可以得到对数与指数间的关系:
由指数和对数的这个关系,可以得到关于对数的如下结论:
(真数一定为正数)
利用对数与指数间的关系证明这两个结论.
因为ax=N,(a>0且a≠1),由指数函数的性质可知:N>0,所以负数和
0没有对数. (真数N一定为正数)
(1) log 64 x= ; (2) logx8=6;
(3) lg100=x; (4) -ln e2 =x.
例2 求下列各式中的x 的值:
03
拓 展 提 升
Expansion And Promotion
练习1 求下列各式的值:
(1) ; (2) .
练习2 求下列各式中的x 的值:
(1) lg(ln x)=0 ; (2) lg(ln x)=1 ; (3) log7[log3(log2x)]=0 .
04
归 纳 总 结
Sum Up
1. 对数的概念:
一般地,如果ax=N,(a>0且a≠1),则数x叫做以a为底N的对数记作x=logaN,其中a叫底数,N叫真数. (真数一定为正数)
2. 对数的性质:
05
课 后 作 业
Homework After Class
课本126页 习题4.3 第1题
求下列各式中x的值
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
