省级教学竞赛获奖课件5.2.2同角三角函数的基本关系 课件(共26张PPT)
文档属性
| 名称 | 省级教学竞赛获奖课件5.2.2同角三角函数的基本关系 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 519.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 09:24:04 | ||
图片预览





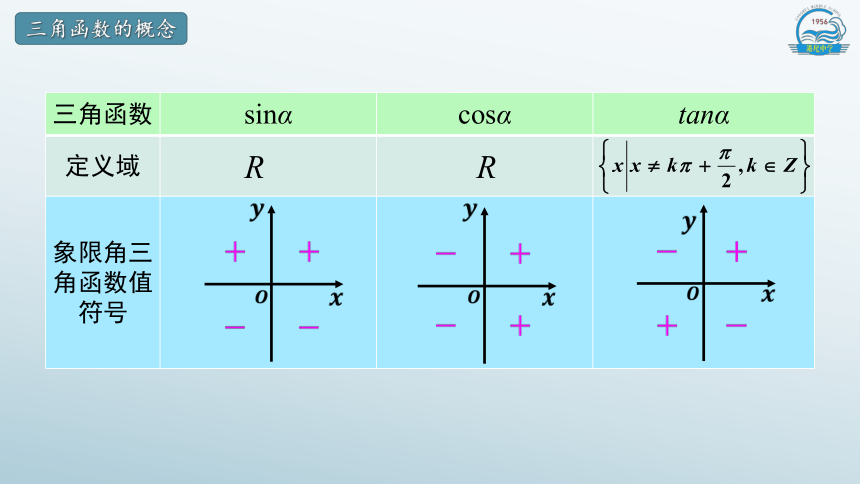



文档简介
(共26张PPT)
第五章 三角函数
5.2.2 同角三角函数的基本关系
教学目标
理解并掌握同角三角函数的基本关系;(重点)
01
会用同角三角函数的基本关系进行三角函数式的求值、化简和证明;
(重点、难点)
02
通过对同角三角函数的基本关系式的探究学习,让学生学会用联系的观
点,化归与转化的思想,数形结合的思想分析解决问题,培养探究精神
和创新意识.
03
学科素养
理解并掌握同角三角函数的基本关系;
数学抽象
直观想象
用同角三角函数的基本关系进行三角函数式的求值、化简和证明;
逻辑推理
用同角三角函数的基本关系进行三角函数式的求值、化简和证明;
数学运算
数据分析
数学建模
01
知 识 回 顾
Retrospective Knowledge
设α是一个任意角,α∈R,它的终边与单位圆相交于点P(x,y)
(1)把点P的纵坐标y叫做α的正弦函数,记作sinα,即y=sinα;
(2)把点P的横坐标x叫做α的余弦函数,记作cosα,即x=cosα;
(3)把点P的纵坐标和横坐标的比值 叫做α的 ,记作 ,即 (x≠0).
终边相同的角的对应三角函数相同:
cos(α+2kπ)=cosα
tan(α+2kπ)=tanα
sin(α+2kπ)=sinα
其中k∈Z
三角函数的概念
三角函数 sinα cosα tanα
定义域
象限角三角函数值 符号
三角函数的概念
02
新 知 探 索
New Knowledge explore
因为三个三角函数值都是由角的终边与单位圆的交点坐标所唯一确定的,所以它们之间一定有内在联系.由公式一可知,我们不妨讨论同一个角的三个三角函数值之间的关系.
公式一表明,终边相同的角的同一三角函数值相等.那么,终边相同的角的三个三角函数之间是否也有某种关系呢?
探究
如图,设点P(x,x)是角α的终边与单位圆的交点,过P作x轴的垂线,交x轴于M,则 OMP是直角三角形,且OP=1,由勾股定理有:OM2+MP2=1.
因此x2+y2=1,即
显然,当α的终边与坐标轴重合时,这个公式也成立.
根据三角函数的定义,当 时,有
也就是说,同一个角α的正弦、余弦的
平方和等于1; 商(有意义)等于角α的正切.
【例1】已知 ,求cos α,tan α的值.
【解析】因为sin α<0,sin α≠-1,所以α是第三或第四象限角.
由sin2α+cos2α=1得cos2α=1-sin2α= ;
如果α是第三象限角,那么cos α<0.于是cosα= ,
从而 .
如果α是第四象限角,那么cos α>0.于是cos α= ,
从而 .
步骤:
第一步,先根据条件判断角所在的象限;
第二步,确定各三角函数值的符号;
第三步,利用基本关系求解.
同角三角函数的两个基本关系式: 和 中有sin α,cos α,tan α这三个量,故知道其中一个即可求出另外两个.
利用同角三角函数的两个基本关系式,“知一个求其二”.
题型一. 已知sin α(或cos α),求cos α(或sin α),tan α.
题型二. 已知tan α,求cos α,sin α.
03
拓 展 提 升
Expansion And Promotion
例题4的第1小题和第2小题的解法二叫做“齐次化切”.
“齐次化切”适用题型特点:
(1)式子由正弦、余弦组成;
(2)分式结构或可化成分式结构;
(3)每一项次幂相同.
04
归 纳 总 结
Sum Up
同角三角函数的两个基本关系式: 和 中sin α,cos α,tan α这三个量,知一可求其二.
步骤:第一步,先根据条件判断角所在的象限;第二步,确定各三角函数值的符号;
第三步,利用基本关系求解.
“齐次化切”适用题型特点:
(1)式子由正弦、余弦组成;(2)分式结构或可化成分式结构;(3)每一项次幂相同.
这两个式子中sin α+cos α,sin α-cos α,sin αcos α这三个量,知一可求其二.
05
课 后 作 业
Homework After Class
第五章 三角函数
5.2.2 同角三角函数的基本关系
教学目标
理解并掌握同角三角函数的基本关系;(重点)
01
会用同角三角函数的基本关系进行三角函数式的求值、化简和证明;
(重点、难点)
02
通过对同角三角函数的基本关系式的探究学习,让学生学会用联系的观
点,化归与转化的思想,数形结合的思想分析解决问题,培养探究精神
和创新意识.
03
学科素养
理解并掌握同角三角函数的基本关系;
数学抽象
直观想象
用同角三角函数的基本关系进行三角函数式的求值、化简和证明;
逻辑推理
用同角三角函数的基本关系进行三角函数式的求值、化简和证明;
数学运算
数据分析
数学建模
01
知 识 回 顾
Retrospective Knowledge
设α是一个任意角,α∈R,它的终边与单位圆相交于点P(x,y)
(1)把点P的纵坐标y叫做α的正弦函数,记作sinα,即y=sinα;
(2)把点P的横坐标x叫做α的余弦函数,记作cosα,即x=cosα;
(3)把点P的纵坐标和横坐标的比值 叫做α的 ,记作 ,即 (x≠0).
终边相同的角的对应三角函数相同:
cos(α+2kπ)=cosα
tan(α+2kπ)=tanα
sin(α+2kπ)=sinα
其中k∈Z
三角函数的概念
三角函数 sinα cosα tanα
定义域
象限角三角函数值 符号
三角函数的概念
02
新 知 探 索
New Knowledge explore
因为三个三角函数值都是由角的终边与单位圆的交点坐标所唯一确定的,所以它们之间一定有内在联系.由公式一可知,我们不妨讨论同一个角的三个三角函数值之间的关系.
公式一表明,终边相同的角的同一三角函数值相等.那么,终边相同的角的三个三角函数之间是否也有某种关系呢?
探究
如图,设点P(x,x)是角α的终边与单位圆的交点,过P作x轴的垂线,交x轴于M,则 OMP是直角三角形,且OP=1,由勾股定理有:OM2+MP2=1.
因此x2+y2=1,即
显然,当α的终边与坐标轴重合时,这个公式也成立.
根据三角函数的定义,当 时,有
也就是说,同一个角α的正弦、余弦的
平方和等于1; 商(有意义)等于角α的正切.
【例1】已知 ,求cos α,tan α的值.
【解析】因为sin α<0,sin α≠-1,所以α是第三或第四象限角.
由sin2α+cos2α=1得cos2α=1-sin2α= ;
如果α是第三象限角,那么cos α<0.于是cosα= ,
从而 .
如果α是第四象限角,那么cos α>0.于是cos α= ,
从而 .
步骤:
第一步,先根据条件判断角所在的象限;
第二步,确定各三角函数值的符号;
第三步,利用基本关系求解.
同角三角函数的两个基本关系式: 和 中有sin α,cos α,tan α这三个量,故知道其中一个即可求出另外两个.
利用同角三角函数的两个基本关系式,“知一个求其二”.
题型一. 已知sin α(或cos α),求cos α(或sin α),tan α.
题型二. 已知tan α,求cos α,sin α.
03
拓 展 提 升
Expansion And Promotion
例题4的第1小题和第2小题的解法二叫做“齐次化切”.
“齐次化切”适用题型特点:
(1)式子由正弦、余弦组成;
(2)分式结构或可化成分式结构;
(3)每一项次幂相同.
04
归 纳 总 结
Sum Up
同角三角函数的两个基本关系式: 和 中sin α,cos α,tan α这三个量,知一可求其二.
步骤:第一步,先根据条件判断角所在的象限;第二步,确定各三角函数值的符号;
第三步,利用基本关系求解.
“齐次化切”适用题型特点:
(1)式子由正弦、余弦组成;(2)分式结构或可化成分式结构;(3)每一项次幂相同.
这两个式子中sin α+cos α,sin α-cos α,sin αcos α这三个量,知一可求其二.
05
课 后 作 业
Homework After Class
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
