苏教版(2019)高中数学必修第二册 9.2.1 向量的基本运算 练习(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 9.2.1 向量的基本运算 练习(解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 276.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 12:19:46 | ||
图片预览




文档简介
9.2.1向量的基本运算
基础达标
一、选择题
1.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则+等于( )
A. B. C. D.
2.化简-+所得的结果是( )
A. B. C.0 D.
3.如图所示,在平行四边形ABCD中,++等于( )
A. B.
C. D.
4.在边长为1的正三角形ABC中,|-|的值为( )
A.1 B.2 C. D.
5.在矩形ABCD中,||=4,||=2,则向量++的长度为( )
A.2 B.4 C.12 D.6
6.在△ABC中,已知D是AB边上的一点,若=2,=+λ,则λ等于( )
A. B. C. D.
7.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+等于( )
A. B. C. D.
8.已知P,A,B,C是平面内四点,且++=,则下列向量一定共线的是( )
A.与 B.与
C.与 D.与
9.(多选题)已知e1,e2是不共线的向量,下列向量a,b共线的有( )
A.a=e1,b=-2e2
B.a=e1-3e2,b=-2e1+6e2
C.a=3e1-e2,b=2e1-e2
D.a=e1+e2,b=e1-3e2
二、填空题
10.已知O,A,B是平面上的三个点,直线AB上有一点C,满足2+=0,则可用,表示为________.
11.已知点G是△ABC的重心,则++=________.
12.小船以10 km/h的静水速度按垂直于对岸的方向行驶,同时河水的流速为
10 km/h,则小船实际航行速度的大小为________ km/h.
13.已知在△ABC中,点M满足++=0,若存在实数m使得+=m成立,则m=________.
14.已知O,A,B是平面内任意三点,点P在直线AB上,若=3+x,则x=________.
三、解答题
15.如图所示,已知=a,=b,=c,=e,=d,=f,试用a,b,c,d,e,f表示,,-,+,-,++.
16.如图,平行四边形ABCD中,对角线AC与BD交于O点,P为平面内任意一点.
求证:+++=4.
17.在 ABCD中,=a,=b,=3,M为BC的中点,求(用a,b表示).
能力提升
1.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若=a,=b,则等于( )
A.a+b B.a+b
C.a+b D.a+b
2.(多选题)设a=(+)+(+),b是一个非零向量,则下列结论正确的有( )
A.a∥b B.a+b=a
C.a+b=b D.|a+b|<|a|+|b|
3.(多填题)在边长为1的等边三角形ABC中,|+|=______,|+|=________.
4.设点M是线段BC的中点,点A在直线BC外,且||=4,|+|=|-|,则||=________.
5.如图所示,P,Q是△ABC的边BC上两点,且BP=QC.求证:+=+.
6.如图所示,已知在平行四边形ABCD中,=a,=b.求
(1)当a,b满足什么条件时,a+b与a-b垂直;
(2)当a,b满足什么条件时,|a+b|=|a-b|.
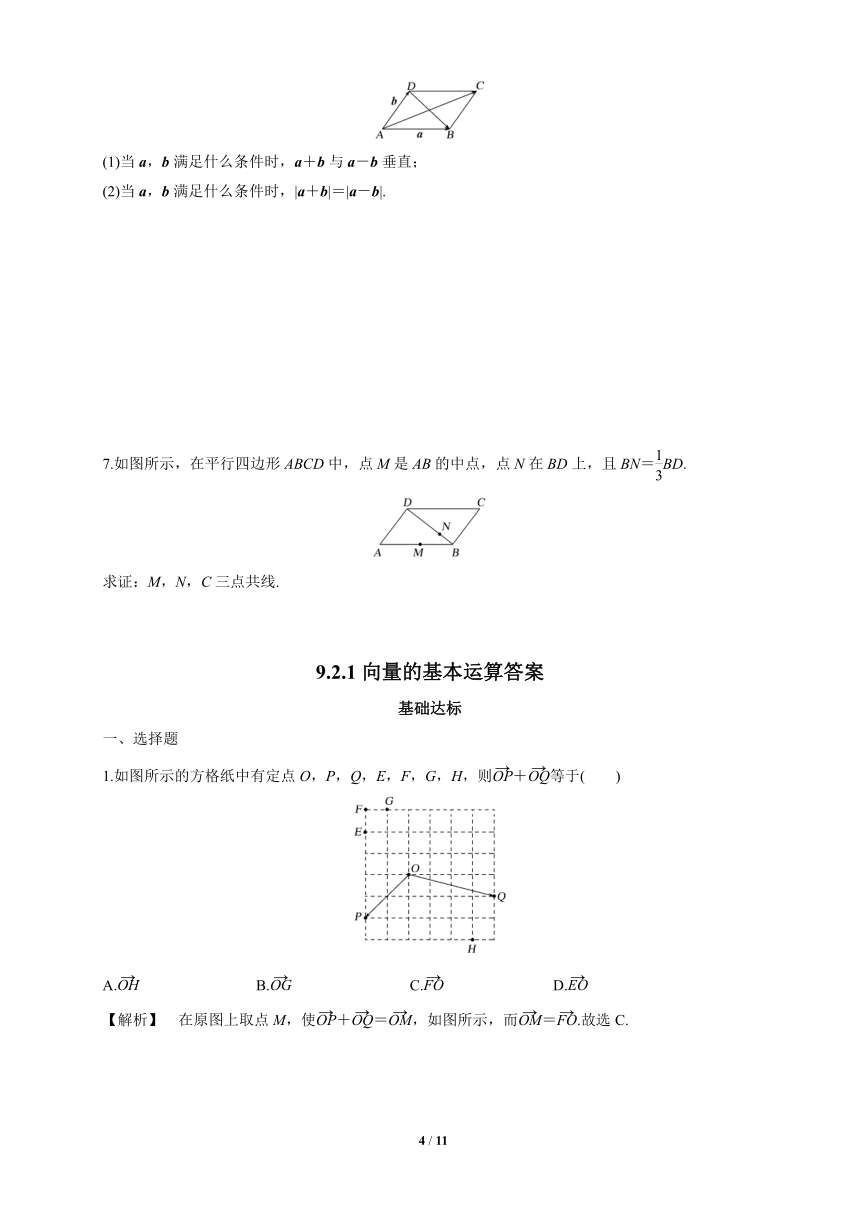
7.如图所示,在平行四边形ABCD中,点M是AB的中点,点N在BD上,且BN=BD.
求证:M,N,C三点共线.
9.2.1向量的基本运算答案
基础达标
一、选择题
1.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则+等于( )
A. B. C. D.
【解析】 在原图上取点M,使+=,如图所示,而=.故选C.
【答案】 C
2.化简-+所得的结果是( )
A. B. C.0 D.
【解析】 -+=+=0.
【答案】 C
3.如图所示,在平行四边形ABCD中,++等于( )
A. B.
C. D.
【解析】 ++=+(+)=+0=.
【答案】 C
4.在边长为1的正三角形ABC中,|-|的值为( )
A.1 B.2 C. D.
【解析】 如图,作菱形ABCD,
则|-|=|-|=||=.
【答案】 D
5.在矩形ABCD中,||=4,||=2,则向量++的长度为( )
A.2 B.4 C.12 D.6
【解析】 因为+=,
所以++的长度为的模的2倍.
又||==2,
所以向量++的长度为4.
【答案】 B
6.在△ABC中,已知D是AB边上的一点,若=2,=+λ,则λ等于( )
A. B. C. D.
【解析】 ∵A,B,D三点共线,∴+λ=1,λ=.
【答案】 B
7.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+等于( )
A. B. C. D.
【解析】 如图,+=+++=+
=(+)=×2=.
【答案】 C
8.已知P,A,B,C是平面内四点,且++=,则下列向量一定共线的是( )
A.与 B.与
C.与 D.与
【解析】 因为++=,
所以+++=0,
即-2=,所以与共线.
【答案】 B
9.(多选题)已知e1,e2是不共线的向量,下列向量a,b共线的有( )
A.a=e1,b=-2e2
B.a=e1-3e2,b=-2e1+6e2
C.a=3e1-e2,b=2e1-e2
D.a=e1+e2,b=e1-3e2
【解析】 因为e1,e2是不共线的向量,
所以e1,e2都不是零向量.
A.若a与b共线,则e1,e2共线,这与已知矛盾,
所以a与b不共线.
B.因为b=-2e1+6e2=-2(e1-3e2)=-2a,
所以a与b共线.
C.因为b=2e1-e2==a,
所以a与b共线.
D.若a与b共线,则存在实数λ∈R,使a=λb,
即e1+e2=λ(e1-3e2),
所以(1-λ)e1+(1+3λ)e2=0.
因为e1,e2是不共线向量,
所以所以λ不存在,
所以a与b不共线.
【答案】 BC
二、填空题
10.已知O,A,B是平面上的三个点,直线AB上有一点C,满足2+=0,则可用,表示为________.
【解析】 =+=+2=+2(-),
∴=2-.
【答案】 2-
11.已知点G是△ABC的重心,则++=________.
【解析】 如图所示,连接AG并延长交BC于点E,点E为BC的中点,延长AE到点D,使ED=GE,则+=,+=0,∴++=0.
【答案】 0
12.小船以10 km/h的静水速度按垂直于对岸的方向行驶,同时河水的流速为
10 km/h,则小船实际航行速度的大小为________ km/h.
【解析】 如图,设船在静水中的速度为|ν1|=10 km/h,河水的流速为|ν2|=10 km/h,小船实际航行速度为ν0,则由|ν1|2+|ν2|2=|ν0|2,得(10)2+102=|ν0|2,所以|ν0|=20 km/h,即小船实际航行速度的大小为20 km/h.
【答案】 20
13.已知在△ABC中,点M满足++=0,若存在实数m使得+=m成立,则m=________.
【解析】 ∵++=0,
∴点M是△ABC的重心.
∴+=3,∴m=3.
【答案】 3
14.已知O,A,B是平面内任意三点,点P在直线AB上,若=3+x,则x=________.
【解析】 因为点P在直线AB上,
所以=λ,λ∈R,-=λ(-),
即=λ+(1-λ),所以所以x=-2.
【答案】 -2
三、解答题
15.如图所示,已知=a,=b,=c,=e,=d,=f,试用a,b,c,d,e,f表示,,-,+,-,++.
解 =-=c-a,
=-=d-a,
-==-=d-b,
+=-+-=b-a+f-c,
-==-=f-d,
++=0.
16.如图,平行四边形ABCD中,对角线AC与BD交于O点,P为平面内任意一点.
求证:+++=4.
证明 ∵+++
=+++++++
=4+(+++)
=4+(+)+(+)
=4+0+04.
∴+++=4.
17.在 ABCD中,=a,=b,=3,M为BC的中点,求(用a,b表示).
解 法一 如图所示,在 ABCD中,AC交BD于O点,
则O平分AC和BD.
∵=3,∴=,
∴N为OC的中点,
又M为BC的中点,∴MN綉BO,
∴===(b-a).
法二 =++=-b-a+
=-b-a+(a+b)=(b-a).
能力提升
1.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若=a,=b,则等于( )
A.a+b B.a+b
C.a+b D.a+b
【解析】 ∵△DEF∽△BEA,∴==,
∴DF=AB=DC,∴=+=+.
∵=+=a,=-=b,
联立得:=(a-b),=(a+b),
∴=(a+b)+(a-b)=a+b.
【答案】 D
2.(多选题)设a=(+)+(+),b是一个非零向量,则下列结论正确的有( )
A.a∥b B.a+b=a
C.a+b=b D.|a+b|<|a|+|b|
【解析】 由条件得:(+)+(+)=0=a,故选AC.
【答案】 AC
3.(多填题)在边长为1的等边三角形ABC中,|+|=______,|+|=________.
【解析】 易知|+|=||=1,以AB,AC为邻边作平行四边形ABDC,则|+|=||=2||×sin 60°=2×1×=.
【答案】 1
4.设点M是线段BC的中点,点A在直线BC外,且||=4,|+|=|-|,则||=________.
【解析】 以AB,AC为邻边作平行四边形ACDB,由向量加减法几何意义可知,=+,=-,
∵|+|=|-|,∴||=||,
又||=4,M是线段BC的中点,
∴||=||=||=2.
【答案】 2
5.如图所示,P,Q是△ABC的边BC上两点,且BP=QC.求证:+=+.
证明 =+,
=+,
∴+=+++.
∵与大小相等,方向相反,
∴+=0,
故+=++0=+.
6.如图所示,已知在平行四边形ABCD中,=a,=b.求
(1)当a,b满足什么条件时,a+b与a-b垂直;
(2)当a,b满足什么条件时,|a+b|=|a-b|.
解 (1)若a+b与a-b垂直,即平行四边形的两条对角线互相垂直,则四边形ABCD为菱形,所以a,b应该满足|a|=|b|.
(2)|a+b|=|a-b|表示平行四边形的两条对角线长度相等,这样的平行四边形为矩形,故a,b应互相垂直.
7.如图所示,在平行四边形ABCD中,点M是AB的中点,点N在BD上,且BN=BD.
求证:M,N,C三点共线.
证明 设=a,=b,则由向量减法的三角形法则可知:
=-=-=a-b.
又∵N在BD上且BN=BD,
∴==(+)=(a+b),
∴=-=(a+b)-b
=a-b=,
∴=,∴与共线,
又∵与的公共点为C,∴C,M,N三点共线.
2 / 2
基础达标
一、选择题
1.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则+等于( )
A. B. C. D.
2.化简-+所得的结果是( )
A. B. C.0 D.
3.如图所示,在平行四边形ABCD中,++等于( )
A. B.
C. D.
4.在边长为1的正三角形ABC中,|-|的值为( )
A.1 B.2 C. D.
5.在矩形ABCD中,||=4,||=2,则向量++的长度为( )
A.2 B.4 C.12 D.6
6.在△ABC中,已知D是AB边上的一点,若=2,=+λ,则λ等于( )
A. B. C. D.
7.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+等于( )
A. B. C. D.
8.已知P,A,B,C是平面内四点,且++=,则下列向量一定共线的是( )
A.与 B.与
C.与 D.与
9.(多选题)已知e1,e2是不共线的向量,下列向量a,b共线的有( )
A.a=e1,b=-2e2
B.a=e1-3e2,b=-2e1+6e2
C.a=3e1-e2,b=2e1-e2
D.a=e1+e2,b=e1-3e2
二、填空题
10.已知O,A,B是平面上的三个点,直线AB上有一点C,满足2+=0,则可用,表示为________.
11.已知点G是△ABC的重心,则++=________.
12.小船以10 km/h的静水速度按垂直于对岸的方向行驶,同时河水的流速为
10 km/h,则小船实际航行速度的大小为________ km/h.
13.已知在△ABC中,点M满足++=0,若存在实数m使得+=m成立,则m=________.
14.已知O,A,B是平面内任意三点,点P在直线AB上,若=3+x,则x=________.
三、解答题
15.如图所示,已知=a,=b,=c,=e,=d,=f,试用a,b,c,d,e,f表示,,-,+,-,++.
16.如图,平行四边形ABCD中,对角线AC与BD交于O点,P为平面内任意一点.
求证:+++=4.
17.在 ABCD中,=a,=b,=3,M为BC的中点,求(用a,b表示).
能力提升
1.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若=a,=b,则等于( )
A.a+b B.a+b
C.a+b D.a+b
2.(多选题)设a=(+)+(+),b是一个非零向量,则下列结论正确的有( )
A.a∥b B.a+b=a
C.a+b=b D.|a+b|<|a|+|b|
3.(多填题)在边长为1的等边三角形ABC中,|+|=______,|+|=________.
4.设点M是线段BC的中点,点A在直线BC外,且||=4,|+|=|-|,则||=________.
5.如图所示,P,Q是△ABC的边BC上两点,且BP=QC.求证:+=+.
6.如图所示,已知在平行四边形ABCD中,=a,=b.求
(1)当a,b满足什么条件时,a+b与a-b垂直;
(2)当a,b满足什么条件时,|a+b|=|a-b|.
7.如图所示,在平行四边形ABCD中,点M是AB的中点,点N在BD上,且BN=BD.
求证:M,N,C三点共线.
9.2.1向量的基本运算答案
基础达标
一、选择题
1.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则+等于( )
A. B. C. D.
【解析】 在原图上取点M,使+=,如图所示,而=.故选C.
【答案】 C
2.化简-+所得的结果是( )
A. B. C.0 D.
【解析】 -+=+=0.
【答案】 C
3.如图所示,在平行四边形ABCD中,++等于( )
A. B.
C. D.
【解析】 ++=+(+)=+0=.
【答案】 C
4.在边长为1的正三角形ABC中,|-|的值为( )
A.1 B.2 C. D.
【解析】 如图,作菱形ABCD,
则|-|=|-|=||=.
【答案】 D
5.在矩形ABCD中,||=4,||=2,则向量++的长度为( )
A.2 B.4 C.12 D.6
【解析】 因为+=,
所以++的长度为的模的2倍.
又||==2,
所以向量++的长度为4.
【答案】 B
6.在△ABC中,已知D是AB边上的一点,若=2,=+λ,则λ等于( )
A. B. C. D.
【解析】 ∵A,B,D三点共线,∴+λ=1,λ=.
【答案】 B
7.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+等于( )
A. B. C. D.
【解析】 如图,+=+++=+
=(+)=×2=.
【答案】 C
8.已知P,A,B,C是平面内四点,且++=,则下列向量一定共线的是( )
A.与 B.与
C.与 D.与
【解析】 因为++=,
所以+++=0,
即-2=,所以与共线.
【答案】 B
9.(多选题)已知e1,e2是不共线的向量,下列向量a,b共线的有( )
A.a=e1,b=-2e2
B.a=e1-3e2,b=-2e1+6e2
C.a=3e1-e2,b=2e1-e2
D.a=e1+e2,b=e1-3e2
【解析】 因为e1,e2是不共线的向量,
所以e1,e2都不是零向量.
A.若a与b共线,则e1,e2共线,这与已知矛盾,
所以a与b不共线.
B.因为b=-2e1+6e2=-2(e1-3e2)=-2a,
所以a与b共线.
C.因为b=2e1-e2==a,
所以a与b共线.
D.若a与b共线,则存在实数λ∈R,使a=λb,
即e1+e2=λ(e1-3e2),
所以(1-λ)e1+(1+3λ)e2=0.
因为e1,e2是不共线向量,
所以所以λ不存在,
所以a与b不共线.
【答案】 BC
二、填空题
10.已知O,A,B是平面上的三个点,直线AB上有一点C,满足2+=0,则可用,表示为________.
【解析】 =+=+2=+2(-),
∴=2-.
【答案】 2-
11.已知点G是△ABC的重心,则++=________.
【解析】 如图所示,连接AG并延长交BC于点E,点E为BC的中点,延长AE到点D,使ED=GE,则+=,+=0,∴++=0.
【答案】 0
12.小船以10 km/h的静水速度按垂直于对岸的方向行驶,同时河水的流速为
10 km/h,则小船实际航行速度的大小为________ km/h.
【解析】 如图,设船在静水中的速度为|ν1|=10 km/h,河水的流速为|ν2|=10 km/h,小船实际航行速度为ν0,则由|ν1|2+|ν2|2=|ν0|2,得(10)2+102=|ν0|2,所以|ν0|=20 km/h,即小船实际航行速度的大小为20 km/h.
【答案】 20
13.已知在△ABC中,点M满足++=0,若存在实数m使得+=m成立,则m=________.
【解析】 ∵++=0,
∴点M是△ABC的重心.
∴+=3,∴m=3.
【答案】 3
14.已知O,A,B是平面内任意三点,点P在直线AB上,若=3+x,则x=________.
【解析】 因为点P在直线AB上,
所以=λ,λ∈R,-=λ(-),
即=λ+(1-λ),所以所以x=-2.
【答案】 -2
三、解答题
15.如图所示,已知=a,=b,=c,=e,=d,=f,试用a,b,c,d,e,f表示,,-,+,-,++.
解 =-=c-a,
=-=d-a,
-==-=d-b,
+=-+-=b-a+f-c,
-==-=f-d,
++=0.
16.如图,平行四边形ABCD中,对角线AC与BD交于O点,P为平面内任意一点.
求证:+++=4.
证明 ∵+++
=+++++++
=4+(+++)
=4+(+)+(+)
=4+0+04.
∴+++=4.
17.在 ABCD中,=a,=b,=3,M为BC的中点,求(用a,b表示).
解 法一 如图所示,在 ABCD中,AC交BD于O点,
则O平分AC和BD.
∵=3,∴=,
∴N为OC的中点,
又M为BC的中点,∴MN綉BO,
∴===(b-a).
法二 =++=-b-a+
=-b-a+(a+b)=(b-a).
能力提升
1.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若=a,=b,则等于( )
A.a+b B.a+b
C.a+b D.a+b
【解析】 ∵△DEF∽△BEA,∴==,
∴DF=AB=DC,∴=+=+.
∵=+=a,=-=b,
联立得:=(a-b),=(a+b),
∴=(a+b)+(a-b)=a+b.
【答案】 D
2.(多选题)设a=(+)+(+),b是一个非零向量,则下列结论正确的有( )
A.a∥b B.a+b=a
C.a+b=b D.|a+b|<|a|+|b|
【解析】 由条件得:(+)+(+)=0=a,故选AC.
【答案】 AC
3.(多填题)在边长为1的等边三角形ABC中,|+|=______,|+|=________.
【解析】 易知|+|=||=1,以AB,AC为邻边作平行四边形ABDC,则|+|=||=2||×sin 60°=2×1×=.
【答案】 1
4.设点M是线段BC的中点,点A在直线BC外,且||=4,|+|=|-|,则||=________.
【解析】 以AB,AC为邻边作平行四边形ACDB,由向量加减法几何意义可知,=+,=-,
∵|+|=|-|,∴||=||,
又||=4,M是线段BC的中点,
∴||=||=||=2.
【答案】 2
5.如图所示,P,Q是△ABC的边BC上两点,且BP=QC.求证:+=+.
证明 =+,
=+,
∴+=+++.
∵与大小相等,方向相反,
∴+=0,
故+=++0=+.
6.如图所示,已知在平行四边形ABCD中,=a,=b.求
(1)当a,b满足什么条件时,a+b与a-b垂直;
(2)当a,b满足什么条件时,|a+b|=|a-b|.
解 (1)若a+b与a-b垂直,即平行四边形的两条对角线互相垂直,则四边形ABCD为菱形,所以a,b应该满足|a|=|b|.
(2)|a+b|=|a-b|表示平行四边形的两条对角线长度相等,这样的平行四边形为矩形,故a,b应互相垂直.
7.如图所示,在平行四边形ABCD中,点M是AB的中点,点N在BD上,且BN=BD.
求证:M,N,C三点共线.
证明 设=a,=b,则由向量减法的三角形法则可知:
=-=-=a-b.
又∵N在BD上且BN=BD,
∴==(+)=(a+b),
∴=-=(a+b)-b
=a-b=,
∴=,∴与共线,
又∵与的公共点为C,∴C,M,N三点共线.
2 / 2
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
