1.4 解直角三角形 课件(共23张PPT)
文档属性
| 名称 | 1.4 解直角三角形 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 13:12:43 | ||
图片预览








文档简介
(共23张PPT)
1.4 解直角三角形
北师大版 九年级 下册
教学目标
教学目标:1.理解 解直角三角形的意义.
2.理解解直角三角形的方法并能熟练解题.
3.通过本节的学习进一步提升学生综合分析、解决问题的能力.
教学重点:理解 解直角三角形的意义.
教学难点:理解解直角三角形的方法并能熟练解题.
新知导入
情境引入
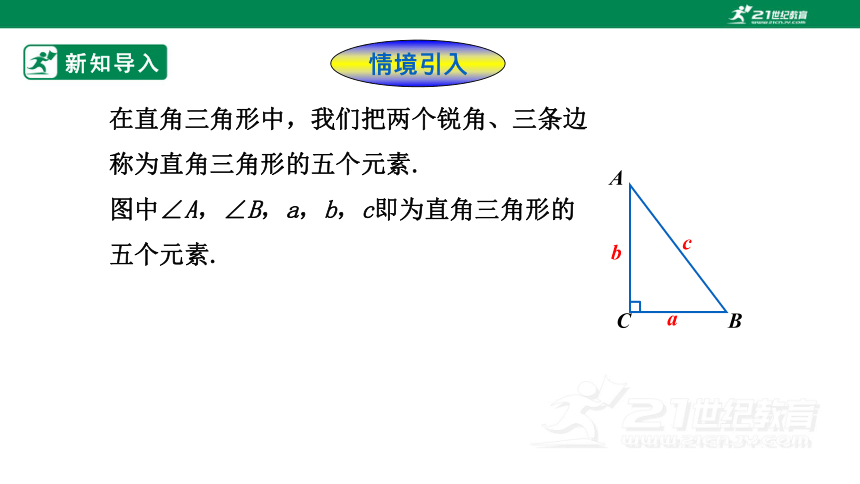
A
B
a
b
c
C
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
新知讲解
合作学习
问题1 在Rt△ABC中,如果已知其中两边的长,你能求出这个三角形的其他元素吗?
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
c2
90°
A
B
a
b
c
C
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
提炼概念
A
B
a
b
c
C
解直角三角形:
在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
典例精讲
【例1】如图,在Rt△ABC中,∠C=90°,a=b=求这个直角三角形的其他元素.
A
B
C
在 Rt△ABC 中,a2+b2=c2,
在 Rt△ABC 中,sinB =
∴∠B = 30°. ∴∠ A = 60°.
解:
想一想
如果已知Rt△ABC中一边和一锐角,你能求出这个三角形其他的元素吗?
若已知一直角边a和一锐角A:①∠B=90 °-∠ A;
②c=
若已知斜边c和一个锐角A:①∠B=90°-∠ A;
②a=c·sin A ; ③b=c·cos A.
例2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为 a,b,c,且b=30,∠B=25°,求这个三角形的其他元素(边长精确到1).
解:Rt△ABC中,∠C=90 ° ,∠B=25°,
∵sinB= ,b=30,
∴c= .
∵tanB= ,b=30,
∴a= .
A
C
B
a
c
b
∴∠A=65 °.
归纳概念
两角
不能
两边
一角一边
在Rt△ABC中,如果已知∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?
总结:在直角三角形的6个元素(即3条边和3个锐角)中,直角是已知元素,如果再知道一条边和第三个元素,这个三角形的所有元素就可以确定下来.
1.做标注:在遇到解直角三形的问题时,先画一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,以得于分析解决问题.
2.找关系式:选取关系式时要尽量利用原始数据,以防止“累积错误”.
3.遵循规则:遵循“有斜用弦,无斜用切;宁乘勿除,化斜为直”.
说说解直角三角形时,有哪些注意点?
课堂练习
1.在Rt△ABC中,∠C=90°,AB=2 ,AC= ,
则∠A的度数为( )
A.90° B.60°
C.45° D.30°
D
2.如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离 BC为( )
A.3sina米 B.3cosa米 C.米 D.米
A
3.在△ABC中,∠C=90°,AB=4,AC=3,欲求∠A的值,最适宜的做法是( )
A.计算tan A的值求出
B.计算sin A的值求出
C.计算cos A的值求出
D.先根据sin B求出∠B,再利用90°-∠B求出
C
4.根据下列条件,解直角三角形:在 Rt △ ABC 中,∠ C=90°,∠ A=30°, b=12.
在 Rt △ ABC 中,∠ C=90°,∠ A=30°,
∴∠ B=90° - ∠ A=60° .
∵ tan A= ∴
∴ a=
解:
5.如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.
D
A
B
C
解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +
6.如图,已知△ABC中,AB=BC=5,tan∠ABC.
设边BC的垂直平分线与边AB的交点为D,求的值.
解:∵DF垂直平分BC,
∴BD=CD,BF=CF,
∵tan∠DBF,
∴DF,
在Rt△BFD中,根据勾股定理得:BD,
∴AD=5,则.
课堂总结
在直角三角形中有三条边、三个角,它们具备以下关系:
(1)三边之间关系:a2+b2=c2 (勾股定理).
(2)锐角之间的关系:∠A+ ∠B = 90°.
(3)边角之间的关系:
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.4 解直角三角形
北师大版 九年级 下册
教学目标
教学目标:1.理解 解直角三角形的意义.
2.理解解直角三角形的方法并能熟练解题.
3.通过本节的学习进一步提升学生综合分析、解决问题的能力.
教学重点:理解 解直角三角形的意义.
教学难点:理解解直角三角形的方法并能熟练解题.
新知导入
情境引入
A
B
a
b
c
C
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
新知讲解
合作学习
问题1 在Rt△ABC中,如果已知其中两边的长,你能求出这个三角形的其他元素吗?
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
c2
90°
A
B
a
b
c
C
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
提炼概念
A
B
a
b
c
C
解直角三角形:
在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
典例精讲
【例1】如图,在Rt△ABC中,∠C=90°,a=b=求这个直角三角形的其他元素.
A
B
C
在 Rt△ABC 中,a2+b2=c2,
在 Rt△ABC 中,sinB =
∴∠B = 30°. ∴∠ A = 60°.
解:
想一想
如果已知Rt△ABC中一边和一锐角,你能求出这个三角形其他的元素吗?
若已知一直角边a和一锐角A:①∠B=90 °-∠ A;
②c=
若已知斜边c和一个锐角A:①∠B=90°-∠ A;
②a=c·sin A ; ③b=c·cos A.
例2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为 a,b,c,且b=30,∠B=25°,求这个三角形的其他元素(边长精确到1).
解:Rt△ABC中,∠C=90 ° ,∠B=25°,
∵sinB= ,b=30,
∴c= .
∵tanB= ,b=30,
∴a= .
A
C
B
a
c
b
∴∠A=65 °.
归纳概念
两角
不能
两边
一角一边
在Rt△ABC中,如果已知∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?
总结:在直角三角形的6个元素(即3条边和3个锐角)中,直角是已知元素,如果再知道一条边和第三个元素,这个三角形的所有元素就可以确定下来.
1.做标注:在遇到解直角三形的问题时,先画一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,以得于分析解决问题.
2.找关系式:选取关系式时要尽量利用原始数据,以防止“累积错误”.
3.遵循规则:遵循“有斜用弦,无斜用切;宁乘勿除,化斜为直”.
说说解直角三角形时,有哪些注意点?
课堂练习
1.在Rt△ABC中,∠C=90°,AB=2 ,AC= ,
则∠A的度数为( )
A.90° B.60°
C.45° D.30°
D
2.如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离 BC为( )
A.3sina米 B.3cosa米 C.米 D.米
A
3.在△ABC中,∠C=90°,AB=4,AC=3,欲求∠A的值,最适宜的做法是( )
A.计算tan A的值求出
B.计算sin A的值求出
C.计算cos A的值求出
D.先根据sin B求出∠B,再利用90°-∠B求出
C
4.根据下列条件,解直角三角形:在 Rt △ ABC 中,∠ C=90°,∠ A=30°, b=12.
在 Rt △ ABC 中,∠ C=90°,∠ A=30°,
∴∠ B=90° - ∠ A=60° .
∵ tan A= ∴
∴ a=
解:
5.如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.
D
A
B
C
解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +
6.如图,已知△ABC中,AB=BC=5,tan∠ABC.
设边BC的垂直平分线与边AB的交点为D,求的值.
解:∵DF垂直平分BC,
∴BD=CD,BF=CF,
∵tan∠DBF,
∴DF,
在Rt△BFD中,根据勾股定理得:BD,
∴AD=5,则.
课堂总结
在直角三角形中有三条边、三个角,它们具备以下关系:
(1)三边之间关系:a2+b2=c2 (勾股定理).
(2)锐角之间的关系:∠A+ ∠B = 90°.
(3)边角之间的关系:
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
