人教版九年级数学上册24.1.2垂直于弦的直径导学练(附答案)
文档属性
| 名称 | 人教版九年级数学上册24.1.2垂直于弦的直径导学练(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 150.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-07 00:00:00 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版九年级数学上册垂直于弦的直径导学练(附答案)
一、单选题
1.已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有( )
A. 4个 B. 3个 C. 2个 D. 1个
2.抛一个铁球,在泥地上砸了一个直径 ,深 的坑,这个铁球的直径是( )
A. B. C. D.
3.如图①是半径为2的半圆,点C是弧AB的中点,现将半圆如图②方式翻折,使得点C与圆心O重合,则图中阴影部分的面积是( )
A. B. C. D.
4.下列说法错误的是( )
A. 直径是弦 B. 最长的弦是直径 C. 垂直弦的直径平分弦 D. 任意三个点确定一个圆
5.如图,⊙O的直径AB=12,CD是⊙O的 弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( )
A. B. C. D.
二、填空题
6.如图,水平放置的圆柱形排水管道的截面直径是1m,排水管内水的最大深度CD是0.8m,则水面宽AB为________ m.
7题
7.如图,⊙O的直径CD=10,弦AB=8,AB⊥CD,垂足为M,则DM的长为________.
8.如图,AB为⊙O直径,E是BC中点,OE交BC于点D,BD=3,AB=10,则AC=________.
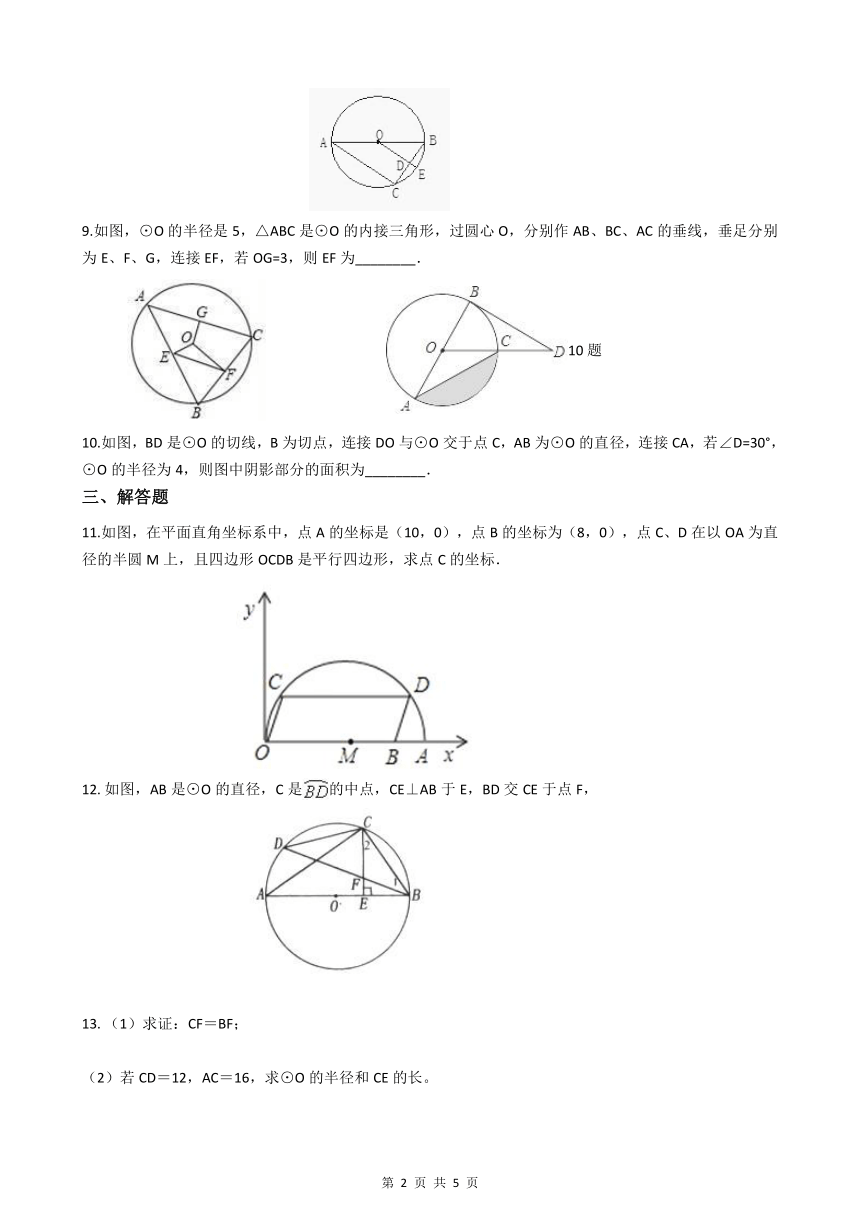
9.如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O,分别作AB、BC、AC的垂线,垂足分别为E、F、G,连接EF,若OG=3,则EF为________.
10题
10.如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4,则图中阴影部分的面积为________.
三、解答题
11.如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标.
如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长。
14.如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD= ,以O为圆心,OC为半径作 ,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
15.如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若CD=2,AB=8,求半径的长.
答 案
一、单选题
1. B 2. B 3. D 4. D 5. A
二、填空题
6. 0.8 7. 8 8. 8 9. 4 10. π﹣4
三、解答题
11. 解:∵四边形OCDB是平行四边形,点B的坐标为(8,0),
CD∥OA,CD=OB=8
过点M作MF⊥CD于F,则CF=CD=4
过C作CE⊥OA于E,
∵A(10,0),∴OA=10,OM=5
∴OE=OM﹣ME=OM﹣CF=5﹣4=1
连接MC,MC=OA=5∴在Rt△CMF中,
MF===3
∴点C的坐标为(1,3)
12. (1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB,∴∠CEB=90°,∴∠2=90°-∠ABC=∠A,
又∵C是弧BD的中点,
∴∠1=∠A,∴∠1=∠2,∴CF=BF;
(2)解:∵C是的中点,
∴=, ∴BC=CD=12,
又∵在Rt△ABC中,AC=16,
∴由勾股定理可得:AB=20,∴⊙O的半径为10,
∵S△ABC=AC BC=AB CE,∴CE==9.6.
13. (1)解:连接OD,
∵OA⊥OB,∴∠AOB=90°,
∵CD∥OB,∴∠OCD=90°,
在RT△OCD中,∵C是AO中点,CD= ,
∴OD=2CO,设OC=x,
∴x2+( )2=(2x)2 , ∴x=1,
∴OD=2,∴⊙O的半径为2
(2)解:∵sin∠CDO= = ,
∴∠CDO=30°,
∵FD∥OB,
∴∠DOB=∠ODC=30°,
∴S圆=S△CDO+S扇形OBD﹣S扇形OCE
= × + ﹣
= +
14. (1)解:∵OD⊥AB,
∴ ,
∵∠AOD=52°,
∴∠DEB= ×52°=26°.
(2)解:设⊙O的半径为x,
则OC=OD-CD=x-2,
∵OD⊥AB,
∴AC= AB= ×8=4,
在Rt△AOC中,OA2=AC2+OC2 ,
∴x2=42+(x-2)2 ,
解得:x=5,
∴⊙O的半径为5.
(
第
- 1 -
页 共
6
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版九年级数学上册垂直于弦的直径导学练(附答案)
一、单选题
1.已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有( )
A. 4个 B. 3个 C. 2个 D. 1个
2.抛一个铁球,在泥地上砸了一个直径 ,深 的坑,这个铁球的直径是( )
A. B. C. D.
3.如图①是半径为2的半圆,点C是弧AB的中点,现将半圆如图②方式翻折,使得点C与圆心O重合,则图中阴影部分的面积是( )
A. B. C. D.
4.下列说法错误的是( )
A. 直径是弦 B. 最长的弦是直径 C. 垂直弦的直径平分弦 D. 任意三个点确定一个圆
5.如图,⊙O的直径AB=12,CD是⊙O的 弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( )
A. B. C. D.
二、填空题
6.如图,水平放置的圆柱形排水管道的截面直径是1m,排水管内水的最大深度CD是0.8m,则水面宽AB为________ m.
7题
7.如图,⊙O的直径CD=10,弦AB=8,AB⊥CD,垂足为M,则DM的长为________.
8.如图,AB为⊙O直径,E是BC中点,OE交BC于点D,BD=3,AB=10,则AC=________.
9.如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O,分别作AB、BC、AC的垂线,垂足分别为E、F、G,连接EF,若OG=3,则EF为________.
10题
10.如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4,则图中阴影部分的面积为________.
三、解答题
11.如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标.
如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长。
14.如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD= ,以O为圆心,OC为半径作 ,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
15.如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若CD=2,AB=8,求半径的长.
答 案
一、单选题
1. B 2. B 3. D 4. D 5. A
二、填空题
6. 0.8 7. 8 8. 8 9. 4 10. π﹣4
三、解答题
11. 解:∵四边形OCDB是平行四边形,点B的坐标为(8,0),
CD∥OA,CD=OB=8
过点M作MF⊥CD于F,则CF=CD=4
过C作CE⊥OA于E,
∵A(10,0),∴OA=10,OM=5
∴OE=OM﹣ME=OM﹣CF=5﹣4=1
连接MC,MC=OA=5∴在Rt△CMF中,
MF===3
∴点C的坐标为(1,3)
12. (1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB,∴∠CEB=90°,∴∠2=90°-∠ABC=∠A,
又∵C是弧BD的中点,
∴∠1=∠A,∴∠1=∠2,∴CF=BF;
(2)解:∵C是的中点,
∴=, ∴BC=CD=12,
又∵在Rt△ABC中,AC=16,
∴由勾股定理可得:AB=20,∴⊙O的半径为10,
∵S△ABC=AC BC=AB CE,∴CE==9.6.
13. (1)解:连接OD,
∵OA⊥OB,∴∠AOB=90°,
∵CD∥OB,∴∠OCD=90°,
在RT△OCD中,∵C是AO中点,CD= ,
∴OD=2CO,设OC=x,
∴x2+( )2=(2x)2 , ∴x=1,
∴OD=2,∴⊙O的半径为2
(2)解:∵sin∠CDO= = ,
∴∠CDO=30°,
∵FD∥OB,
∴∠DOB=∠ODC=30°,
∴S圆=S△CDO+S扇形OBD﹣S扇形OCE
= × + ﹣
= +
14. (1)解:∵OD⊥AB,
∴ ,
∵∠AOD=52°,
∴∠DEB= ×52°=26°.
(2)解:设⊙O的半径为x,
则OC=OD-CD=x-2,
∵OD⊥AB,
∴AC= AB= ×8=4,
在Rt△AOC中,OA2=AC2+OC2 ,
∴x2=42+(x-2)2 ,
解得:x=5,
∴⊙O的半径为5.
(
第
- 1 -
页 共
6
页
)
同课章节目录
