数学人教A版(2019)必修第一册5.2.1 三角函数的概念(共35张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.2.1 三角函数的概念(共35张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 15:49:23 | ||
图片预览








文档简介
(共35张PPT)
5.2.1 三角函数的概念
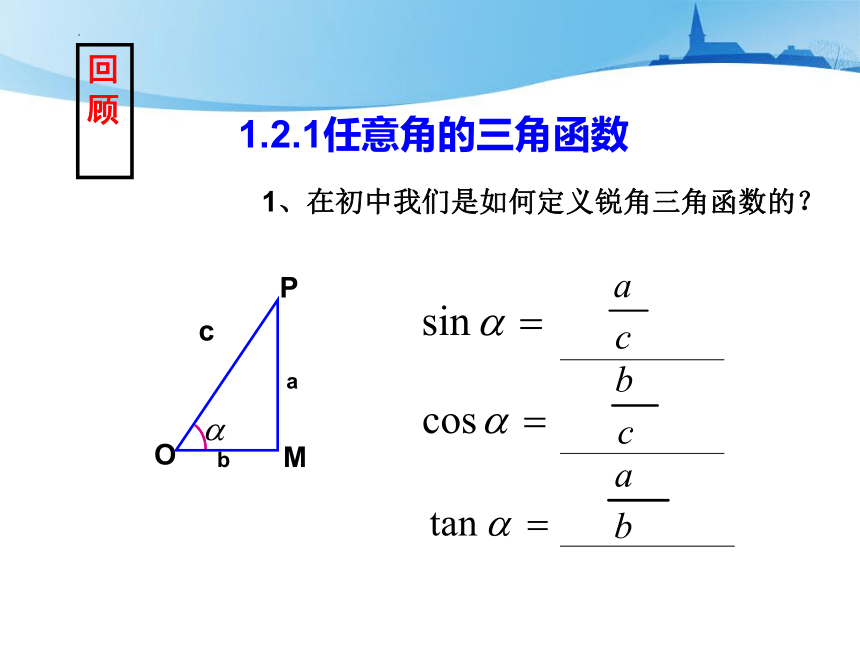
1、在初中我们是如何定义锐角三角函数的?
O
a
b
M
P
c
1.2.1任意角的三角函数
回 顾
y
x
2.在直角坐标系中如何用坐标表示锐角三角函数?
﹒
﹒
o
如果改变点P在终边上的位置,这三个比值会改变吗?
﹒
∽
M
O
y
x
P(a,b)
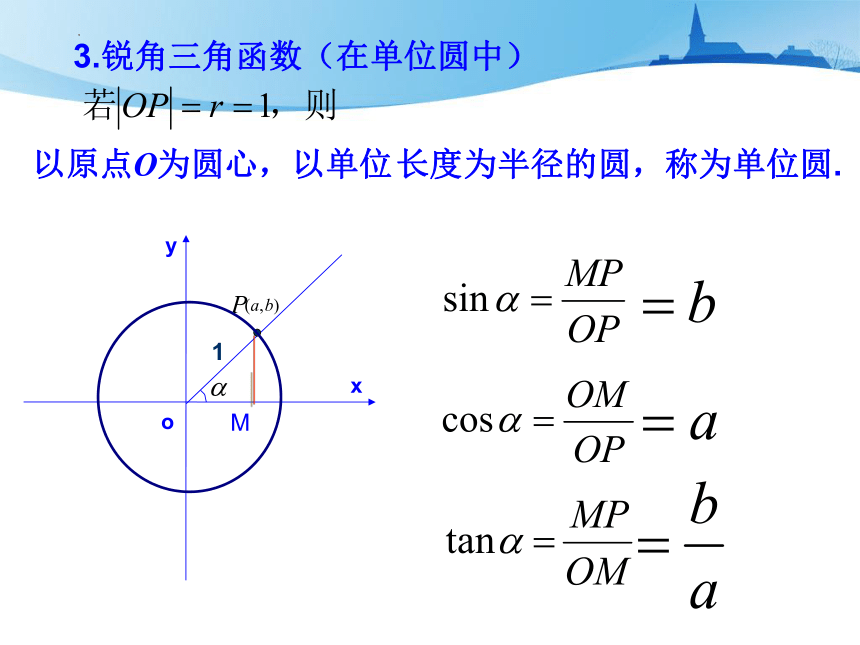
3.锐角三角函数(在单位圆中)
以原点O为圆心,以单位
长度为半径的圆,称为单位圆.
y
o
x
1
M
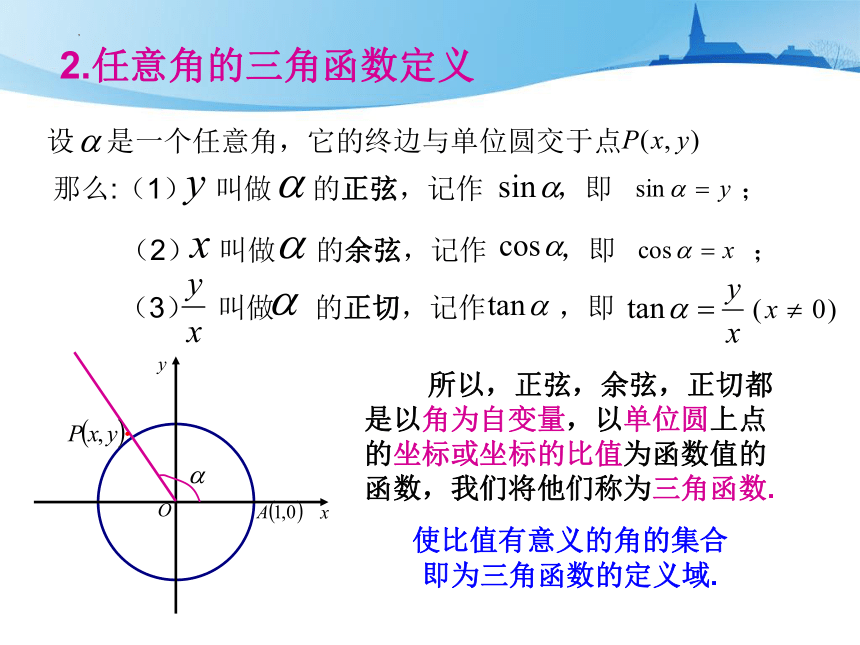
2.任意角的三角函数定义
设 是一个任意角,它的终边与单位圆交于点
那么:(1) 叫做 的正弦,记作 ,即 ;
(2) 叫做 的余弦,记作 ,即 ;
(3) 叫做 的正切,记作 ,即 。
所以,正弦,余弦,正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将他们称为三角函数.
﹒
使比值有意义的角的集合
即为三角函数的定义域.
例1 求 的正弦、余弦和正切值.
解:在直角坐标系中,作
,易知
的终边与单位圆的交点坐标为
所以
思考:若把角 改为 呢
,
,
﹒
﹒
【例2】如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r.求证:
【解析】设α的终边与单位圆交于点P0(x0,y0),分别过点P,P0作x轴的垂线PM,P0M0,垂足分别为M,M0,则: |P0M0|=|y0|,|PM|=|y|,|OM0|=|x0|,|OM|=|x|,ΔOMP∽ΔOM0P0
α
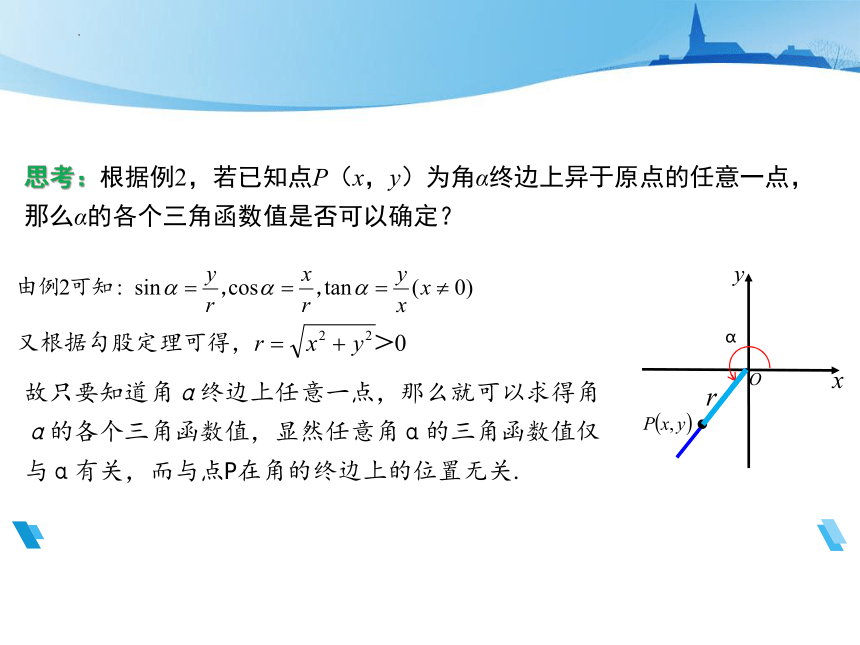
思考:根据例2,若已知点P(x,y)为角α终边上异于原点的任意一点,那么α的各个三角函数值是否可以确定?
α
故只要知道角α终边上任意一点,那么就可以求得角α的各个三角函数值,显然任意角α的三角函数值仅与α有关,而与点P在角的终边上的位置无关.
练习 已知角 的终边经过点 ,求角 的正弦、余弦和正切值 .
解:由已知可得
\
定义法
设角 是一个任意角, 是终边上的任意一点,
点 与原点的距离
那么① 叫做 的正弦,即
② 叫做 的余弦,即
③ 叫做 的正切,即
任意角 的三角函数值仅与 有关,而与点 在角的终边上的位置无关.
定义推广:
于是,
练习 1、已知角 的终边过点 ,
求 的三个三角函数值.
解:由已知可得:
几个特殊角的三角函数值
角α 0o 30o 45o 60o 90o 180o 270o 360o
角α的弧度数
sinα
cosα
tanα
问题2 三角函数符号与公式
1.根据三角函数的定义,确定它们的定义域
(弧度制)
三角函数 定义域
R
2.确定三角函数值在各象限的符号
y
x
o
y
x
o
y
x
o
+
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
R
口诀“一全正, 二正弦,三正切,四余弦.”
+
-
-
+
-
-
+
+
-
+
-
探
究
例3 求证:当且仅当下列不等式组成立时,
角 为第三象限角.
①
②
证明:
因为①式 成立,所以 角的终边可能位于第三 或第四象限,也可能位于y 轴的非正半轴上;
又因为②式 成立,所以角 的终边可能位于第一或第三象限.
因为①②式都成立,所以角 的终边只能位于第三象限.
于是角 为第三象限角.
反过来请同学们自己证明.
思考:
如果两个角的终边相同,那么这两个角的
同一三角函数值有何关系?
终边相同的角的同一三角函数值相等(公式一)
其中
利用公式一,可以把求任意角的三角函数值,转化为
求 角的三角函数值 .
例4 确定下列三角函数值的符号:
(1) (2) (3) (4)
解:
(1)因为 是第三象限角,所以 ;
(3)因为 = ,
而 是第一象限角,所以 ;
练习 确定下列三角函数值的符号
(2)因为 是第四象限角,所以 .
(4)因为 = ,
而 的终边在X轴上,所以 ;
例5 求下列三角函数值:
(1) (2) (3)
(2)
练习 求下列三角函数值
(3)
sin1480°10′,
(1)sin1480°10′=sin(40°10′+4x360°)= sin40°10′≈0.645
解:
15页练习题
1. 内容总结:
①三角函数的概念.
②三角函数的定义域及三角函数值在各象限的符号.
③诱导公式一.
运用了定义法、公式法、数形结合法解题.
划归的思想,数形结合的思想.
2 .方法总结:
3 .体现的数学思想:
三角函数的符号
三角函数在各象限内的符号:
o
x
y
上正下负横为0
o
x
y
三角函数在各象限内的符号:
左负右正纵为0
o
x
y
三角函数在各象限内的符号:
交叉正负
三角函数线
y
x
x
y
y
y
x
x
M
M
M
M
O
O
O
O
P
P
P
P
α的终边
α的终边
α的终边
α的终边
A(1,0)
A(1,0)
A(1,0)
A(1,0)
(Ⅳ)
(Ⅰ)
(Ⅱ)
(Ⅲ)
角α的终边与单位圆交于点P.过点P作x轴的垂线,垂足为M.
|MP|=|y|=|sinα|
|OM|=|x|=|cosα|
三角函数线——正弦线和余弦线
【思考】为了去掉上述等式中的绝对值符号,能否给线段OM、MP规定一个适当的方向,使它们的取值与点P的坐标一致
【定义】有向线段
* 带有方向的线段叫有向线段.
*有向线段的大小称为它的数量.
在坐标系中,规定:
有向线段的方向与坐标系的方向相同.即同向时,数量为正;反向时,数量为负.
y
x
x
y
y
y
x
x
M
M
M
M
O
O
O
O
P
P
P
P
α的终边
α的终边
α的终边
α的终边
A(1,0)
A(1,0)
A(1,0)
A(1,0)
(Ⅳ)
(Ⅰ)
(Ⅱ)
(Ⅲ)
当角α的终边不在坐标轴上时,以M为始点、P为终点,规定:
当线段MP与y轴同向 时,MP的方向为正向,且有正值y;
当线段MP与y轴反向时MP的方向为负向,且有负值y.
MP=y=sinα 有向线段MP叫角α的正弦线
y
x
x
y
y
y
x
x
M
M
M
M
O
O
O
O
P
P
P
P
α的终边
α的终边
α的终边
α的终边
A(1,0)
A(1,0)
A(1,0)
A(1,0)
(Ⅳ)
(Ⅰ)
(Ⅱ)
(Ⅲ)
|MP|=|y|=|sinα|
|OM|=|x|=|cosα|
当角α的终边不在坐标轴上时,以O为始点、M为终点,规定:
当线段OM与x轴同向 时,OM的方向为正向,且有正值x;
当线段OM与x轴反向时,OM的方向为负向,且有负值x.
OM=x=cosα 有向线段OM叫角α的余弦线
T
T
T
y
x
x
y
y
y
x
x
M
M
M
M
O
O
O
O
P
P
P
P
α的终边
α的终边
α的终边
α的终边
A(1,0)
A(1,0)
A(1,0)
A(1,0)
(Ⅳ)
(Ⅰ)
(Ⅱ)
(Ⅲ)
T
过点A(1,0)作单位圆的切线,设它与α的终边或其反向延长线相交于点T.
有向线段AT叫角α的正切线
这三条与单位圆有关的有向线段MP、OM、AT,分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线
y
x
T
M
O
P
α的终边
A(1,0)
当角α的终边与x轴重合时,正弦线、正切线,分别变成一个点,此时角α的正弦值和正切值都为0;
当角α的终边与y轴重合时,余
弦线变成一个点,正切线不存
在,此时角α的正切值不存在.
例1、作出下列各角的正弦线、余弦线、正切线
(1)
π
3
(2) —
2π
3
六、例题
[ Add your company slogan ]
Thank You !
5.2.1 三角函数的概念
1、在初中我们是如何定义锐角三角函数的?
O
a
b
M
P
c
1.2.1任意角的三角函数
回 顾
y
x
2.在直角坐标系中如何用坐标表示锐角三角函数?
﹒
﹒
o
如果改变点P在终边上的位置,这三个比值会改变吗?
﹒
∽
M
O
y
x
P(a,b)
3.锐角三角函数(在单位圆中)
以原点O为圆心,以单位
长度为半径的圆,称为单位圆.
y
o
x
1
M
2.任意角的三角函数定义
设 是一个任意角,它的终边与单位圆交于点
那么:(1) 叫做 的正弦,记作 ,即 ;
(2) 叫做 的余弦,记作 ,即 ;
(3) 叫做 的正切,记作 ,即 。
所以,正弦,余弦,正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将他们称为三角函数.
﹒
使比值有意义的角的集合
即为三角函数的定义域.
例1 求 的正弦、余弦和正切值.
解:在直角坐标系中,作
,易知
的终边与单位圆的交点坐标为
所以
思考:若把角 改为 呢
,
,
﹒
﹒
【例2】如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r.求证:
【解析】设α的终边与单位圆交于点P0(x0,y0),分别过点P,P0作x轴的垂线PM,P0M0,垂足分别为M,M0,则: |P0M0|=|y0|,|PM|=|y|,|OM0|=|x0|,|OM|=|x|,ΔOMP∽ΔOM0P0
α
思考:根据例2,若已知点P(x,y)为角α终边上异于原点的任意一点,那么α的各个三角函数值是否可以确定?
α
故只要知道角α终边上任意一点,那么就可以求得角α的各个三角函数值,显然任意角α的三角函数值仅与α有关,而与点P在角的终边上的位置无关.
练习 已知角 的终边经过点 ,求角 的正弦、余弦和正切值 .
解:由已知可得
\
定义法
设角 是一个任意角, 是终边上的任意一点,
点 与原点的距离
那么① 叫做 的正弦,即
② 叫做 的余弦,即
③ 叫做 的正切,即
任意角 的三角函数值仅与 有关,而与点 在角的终边上的位置无关.
定义推广:
于是,
练习 1、已知角 的终边过点 ,
求 的三个三角函数值.
解:由已知可得:
几个特殊角的三角函数值
角α 0o 30o 45o 60o 90o 180o 270o 360o
角α的弧度数
sinα
cosα
tanα
问题2 三角函数符号与公式
1.根据三角函数的定义,确定它们的定义域
(弧度制)
三角函数 定义域
R
2.确定三角函数值在各象限的符号
y
x
o
y
x
o
y
x
o
+
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
R
口诀“一全正, 二正弦,三正切,四余弦.”
+
-
-
+
-
-
+
+
-
+
-
探
究
例3 求证:当且仅当下列不等式组成立时,
角 为第三象限角.
①
②
证明:
因为①式 成立,所以 角的终边可能位于第三 或第四象限,也可能位于y 轴的非正半轴上;
又因为②式 成立,所以角 的终边可能位于第一或第三象限.
因为①②式都成立,所以角 的终边只能位于第三象限.
于是角 为第三象限角.
反过来请同学们自己证明.
思考:
如果两个角的终边相同,那么这两个角的
同一三角函数值有何关系?
终边相同的角的同一三角函数值相等(公式一)
其中
利用公式一,可以把求任意角的三角函数值,转化为
求 角的三角函数值 .
例4 确定下列三角函数值的符号:
(1) (2) (3) (4)
解:
(1)因为 是第三象限角,所以 ;
(3)因为 = ,
而 是第一象限角,所以 ;
练习 确定下列三角函数值的符号
(2)因为 是第四象限角,所以 .
(4)因为 = ,
而 的终边在X轴上,所以 ;
例5 求下列三角函数值:
(1) (2) (3)
(2)
练习 求下列三角函数值
(3)
sin1480°10′,
(1)sin1480°10′=sin(40°10′+4x360°)= sin40°10′≈0.645
解:
15页练习题
1. 内容总结:
①三角函数的概念.
②三角函数的定义域及三角函数值在各象限的符号.
③诱导公式一.
运用了定义法、公式法、数形结合法解题.
划归的思想,数形结合的思想.
2 .方法总结:
3 .体现的数学思想:
三角函数的符号
三角函数在各象限内的符号:
o
x
y
上正下负横为0
o
x
y
三角函数在各象限内的符号:
左负右正纵为0
o
x
y
三角函数在各象限内的符号:
交叉正负
三角函数线
y
x
x
y
y
y
x
x
M
M
M
M
O
O
O
O
P
P
P
P
α的终边
α的终边
α的终边
α的终边
A(1,0)
A(1,0)
A(1,0)
A(1,0)
(Ⅳ)
(Ⅰ)
(Ⅱ)
(Ⅲ)
角α的终边与单位圆交于点P.过点P作x轴的垂线,垂足为M.
|MP|=|y|=|sinα|
|OM|=|x|=|cosα|
三角函数线——正弦线和余弦线
【思考】为了去掉上述等式中的绝对值符号,能否给线段OM、MP规定一个适当的方向,使它们的取值与点P的坐标一致
【定义】有向线段
* 带有方向的线段叫有向线段.
*有向线段的大小称为它的数量.
在坐标系中,规定:
有向线段的方向与坐标系的方向相同.即同向时,数量为正;反向时,数量为负.
y
x
x
y
y
y
x
x
M
M
M
M
O
O
O
O
P
P
P
P
α的终边
α的终边
α的终边
α的终边
A(1,0)
A(1,0)
A(1,0)
A(1,0)
(Ⅳ)
(Ⅰ)
(Ⅱ)
(Ⅲ)
当角α的终边不在坐标轴上时,以M为始点、P为终点,规定:
当线段MP与y轴同向 时,MP的方向为正向,且有正值y;
当线段MP与y轴反向时MP的方向为负向,且有负值y.
MP=y=sinα 有向线段MP叫角α的正弦线
y
x
x
y
y
y
x
x
M
M
M
M
O
O
O
O
P
P
P
P
α的终边
α的终边
α的终边
α的终边
A(1,0)
A(1,0)
A(1,0)
A(1,0)
(Ⅳ)
(Ⅰ)
(Ⅱ)
(Ⅲ)
|MP|=|y|=|sinα|
|OM|=|x|=|cosα|
当角α的终边不在坐标轴上时,以O为始点、M为终点,规定:
当线段OM与x轴同向 时,OM的方向为正向,且有正值x;
当线段OM与x轴反向时,OM的方向为负向,且有负值x.
OM=x=cosα 有向线段OM叫角α的余弦线
T
T
T
y
x
x
y
y
y
x
x
M
M
M
M
O
O
O
O
P
P
P
P
α的终边
α的终边
α的终边
α的终边
A(1,0)
A(1,0)
A(1,0)
A(1,0)
(Ⅳ)
(Ⅰ)
(Ⅱ)
(Ⅲ)
T
过点A(1,0)作单位圆的切线,设它与α的终边或其反向延长线相交于点T.
有向线段AT叫角α的正切线
这三条与单位圆有关的有向线段MP、OM、AT,分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线
y
x
T
M
O
P
α的终边
A(1,0)
当角α的终边与x轴重合时,正弦线、正切线,分别变成一个点,此时角α的正弦值和正切值都为0;
当角α的终边与y轴重合时,余
弦线变成一个点,正切线不存
在,此时角α的正切值不存在.
例1、作出下列各角的正弦线、余弦线、正切线
(1)
π
3
(2) —
2π
3
六、例题
[ Add your company slogan ]
Thank You !
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
