2023届高三数学二轮复习-最近三年高考数学函数真题(PDF版含解析)
文档属性
| 名称 | 2023届高三数学二轮复习-最近三年高考数学函数真题(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 824.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 16:38:48 | ||
图片预览



文档简介
2020-2022 函数高考题分类合集
一.反函数(上海)
1.(2022上海春考)设函数 f (x) x3的反函数为 f 1(x),则 f 1(27) ________.
2.(2021上海春季)下列函数中,在定义域内存在反函数的是( )
A. f (x) x2 B. f (x) sin x C. f (x) 2x D. f (x) 1
3.(2021 3 1上海)已知 f (x) 2,则 f (1) ________.
x
4.(2020 ) 3 1 1上海 已知函数 f (x) x , f (x)是 f (x)的反函数,则 f (x) ________, x R.
二.具体函数定义域
1.(2022上海春考)下列函数定义域为 R 的是( )
1 1 1
A. y x 2 B. y x 1 C. y x 3 D. y x 2
f (x) 12.(2022北京)函数 1 x 的定义域是________.
x
3.(2020北京)函数 f (x) 1 ln x的定义域是________.
x 1
三.函数的零点与方程根的关系
cos(2 x 2 a) x a
1.(2021天津)设 a R,函数 f (x) 2 ,若函数 f (x)在区间 (0, )
x 2(a 1)x a
2 5 x a
内恰有 6个零点,则 a的取值范围是( )
A (2 9 5 11 7. , ] ( , ] B. ( , 2] (5 11, ]
4 2 4 4 2 4
C. (2 9, ] [11 7 11,3) D. ( , 2) [ ,3)4 4 4 4
2.(2021北京)已知函数 f (x) | lg x | kx 2,给出下列四个结论:
(1)若 k 0 ,则 f (x)有 2个零点;
(2)存在负数 k,使得 f (x)恰有 1个零点;
- 1 -
(3)存在负数 k,使得 f (x)恰有 3个零点;
(4)存在正数 k,使得 f (x)恰有 3个零点.
其中所有正确结论的序号是________.
3
3 (2020 ) x , x 0,. 天津 已知函数 f (x) 若函数 g(x) f (x) | kx2 2x | (k R)恰有 4 个零
x, x 0
点,则 k的取值范围是( )
A. ( 1 , ) (2 2 , ) B. ( 1 , ) (0, 2 2)
2 2
C. ( , 0) (0, 2 2) D. ( , 0) (2 2 , )
4.(2020上海)设 a R,若存在定义域为 R 的函数 f (x)同时满足下列两个条件:
(1)对任意的 x0 R, f (x )的值为 x 或 x
2
0 0 0 ;
(2)关于 x的方程 f (x) a无实数解,
则 a的取值范围是________.
四.分段函数
ax 1, x a,
1. (2022北京)设函数 f x 2 若 f (x)存在最小值,则 a的一个取值为
x 2 , x a.
________;a的最大值为________.
x2 2, x 1,
1
2. (2022浙江)已知函数 f x 1 则 f f ________;若当 x [a,b]
x 1, x 1, 2 x
时,1 f (x) 3,则b a的最大值是________.
2
3 (2021 ) x 4, x 2,. 浙江 已知 a R,函数 f (x) 若 f ( f ( 6)) 3,则 a ________.
| x 3 | a, x 2
4.(2020上海)在研究某市交通情况时,道路密度是指该路段上一定时间内通过的车辆数除
以时间,车辆密度是该路段一定
q
时间内通过的车辆数除以该路段的长度,现定义交通流量为 v , x为道路密度, q为车
x
- 2 -
80
100 135 1 ( ) x ,0 x 40
辆密度,交通流量 v f (x) 3 .
k(x 40) 85,40 x 80
(1)若交通流量 v 95,求道路密度 x的取值范围;
(2)已知道路密度 x 80时,测得交通流量 v 50,求车辆密度 q的最大值.
五.函数的图象与图象的变换
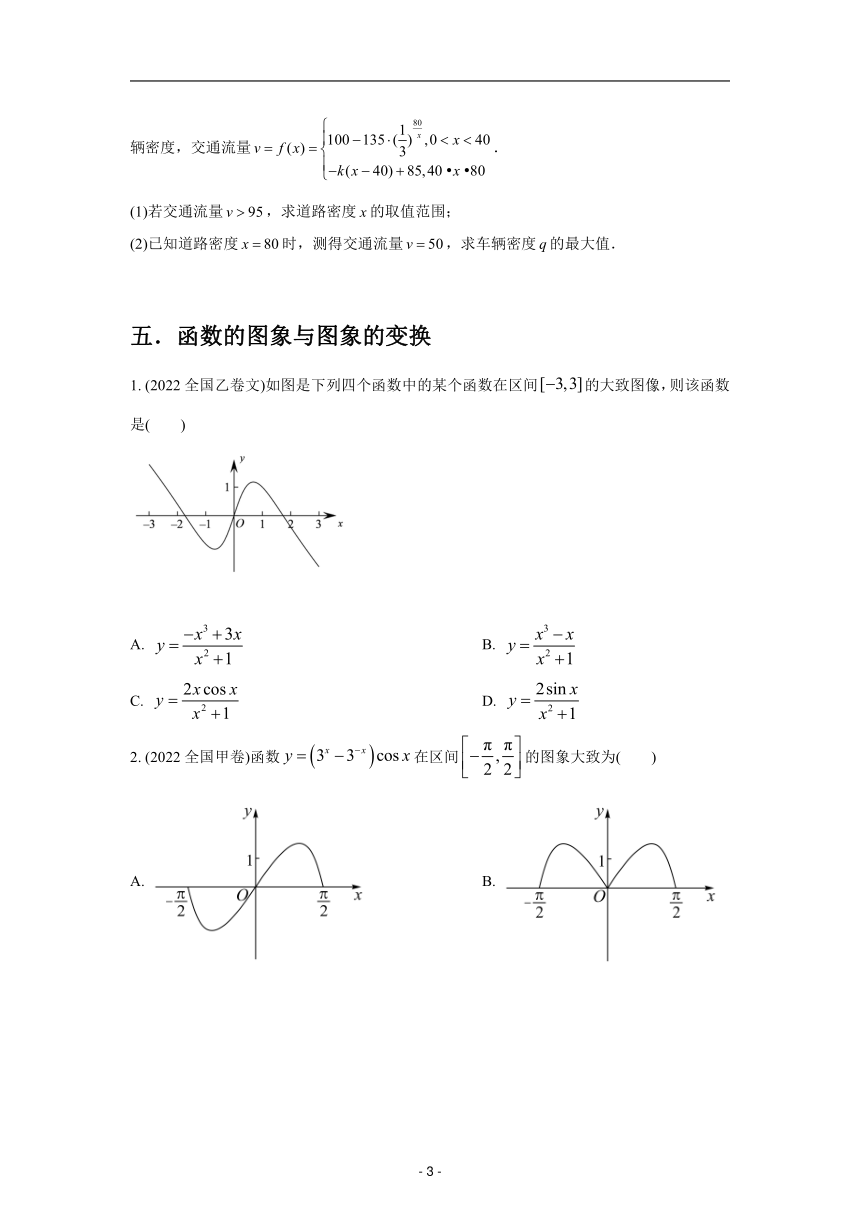
1. (2022全国乙卷文)如图是下列四个函数中的某个函数在区间[ 3,3]的大致图像,则该函数
是( )
x3 3A. y 3x B.2 y
x x
x 1 x2 1
2x cos x 2sin x
C. y 2 D. y x 1 x2 1
2. (2022 x x全国甲卷)函数 y 3 3 cos x π在区间 ,
π
的图象大致为( ) 2 2
A. B.
- 3 -
C. D.
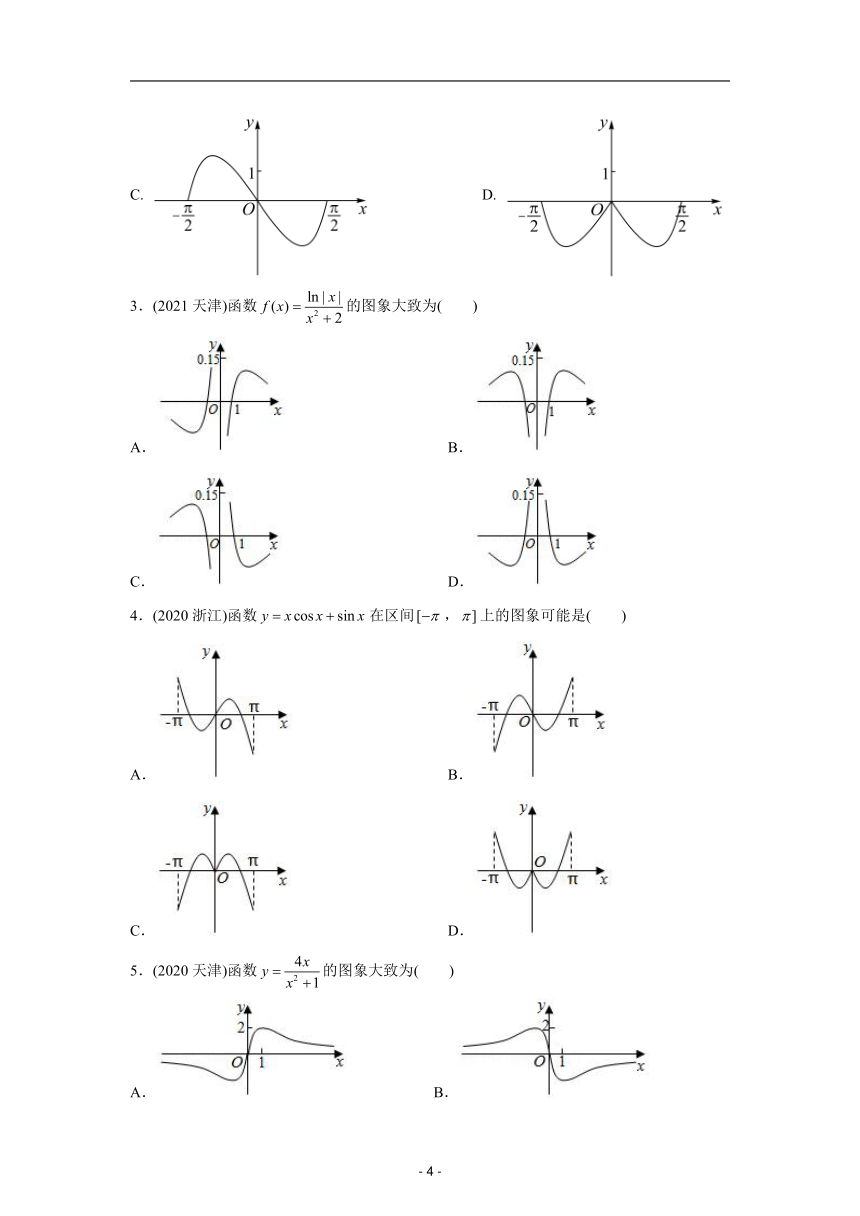
3.(2021 ) ln | x |天津 函数 f (x) 2 的图象大致为( )x 2
A. B.
C. D.
4.(2020浙江)函数 y x cos x sin x 在区间 [ , ]上的图象可能是( )
A. B.
C. D.
5.(2020 4x天津)函数 y 2 的图象大致为( )x 1
A. B.
- 4 -
C. D.
6.(2020北京)为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放
未达标的企业要限期整改.设企业的污水排放量W 与时间 t 的关系为W f (t) ,用
f (b) f (a)
的大小评价在 [a,b]这段时间内企业污水治理能力的强弱.已知整改期内,甲、
b a
乙两企业的污水排放量与时间的关系如图所示.
给出下列四个结论:
①在 [t1, t2 ]这段时间内,甲企业的污水治理能力比乙企业强;
②在 t2 时刻,甲企业的污水治理能力比乙企业强;
③在 t3时刻,甲,乙两企业的污水排放都已达标;
④甲企业在 [0, t1], [t1, t2 ], [t2, t3 ]这三段时间中,在 [0, t1]的污水治理能力最强.
其中所有正确结论的序号是________.
六.函数单调性的性质与判断
1.(2022 上海春考)已知函数 f (x)的定义域为 R,现有两种对 f (x)变换的操作: 变换:
f (x) f (x t); 变换: | f (x t) f (x) |,其中 t为大于 0的常数.
(1)设 f (x) 2x, t 1, g(x)为 f (x)做 变换后的结果,解方程: g(x) 2;
(2)设 f (x) x2, h(x)为 f (x)做 变换后的结果,解不等式: f (x) h(x) ;
(3)设 f (x)在 ( ,0)上单调递增,f (x)先做 变换后得到 u(x),u(x)再做 变换后得到 h1(x);
f (x)先做 变换后得到 v(x), v(x)再做 变换后得到 h2 (x).若 h1(x) h2 (x)恒成立,
证明:函数 f (x)在 R 上单调递增.
- 5 -
2.(2021甲卷文)下列函数中是增函数的为( )
A. f (x) x B. f (x) (2)x C. f (x) x2 D. f (x) 3 x
3
3.(2021上海春季)已知函数 f (x) | x a | a x.
(1)若 a 1,求函数的定义域;
(2)若 a 0,若 f (ax) a有 2个不同实数根,求 a的取值范围;
(3)是否存在实数 a,使得函数 f (x)在定义域内具有单调性?若存在,求出 a的取值范围.
4.(2020上海)命题 p:存在 a R 且 a 0,对于任意的 x R,使得 f (x a) f (x) f (a);
命题 q1 : f (x)单调递减且 f (x) 0恒成立;
命题 q2 : f (x)单调递增,存在 x0 0使得 f (x0 ) 0,
则下列说法正确的是( )
A.只有 q1是 p的充分条件 B.只有 q2是 p的充分条件
C. q1, q2都是 p的充分条件 D. q1, q2都不是 p的充分条件
5.(2020新课标Ⅱ理)若 2x 2y 3 x 3 y ,则( )
A. ln(y x 1) 0 B. ln(y x 1) 0
C. ln | x y | 0 D. ln | x y | 0
七.复合函数的单调性
1 2.(2020海南)已知函数 f (x) lg(x 4x 5)在 (a, )上单调递增,则a的取值范围
是( )
A. (2, ) B.[2, ) C. (5, ) D.[5, )
八.函数奇偶性的性质与判断
1
1. (2022全国乙卷文)若 f x ln a b是奇函数,则a ________,b ________.
1 x
- 6 -
a2x 1 x 0
2.(2022上海)若函数 f (x) x a x 0,为奇函数,求参数 a的值为________.
0 x 0
3. (2022新高考 II)已知函数 f (x)的定义域为 R,且
22
f (x y) f (x y) f (x) f ( y), f (1) 1,则 f (k) ( )
k 1
A. 3 B. 2 C. 0 D. 1
4.(2021甲卷)设函数 f (x)的定义域为 R, f (x 1)为奇函数, f (x 2)为偶函数,当 x [1,
2]时, f (x) ax2 b.若 f (0) f (3) 6 f (9 ,则 ) ( )
2
A 9. B 3 C 7 5. . D.
4 2 4 2
5.(2021乙卷)设函数 f (x) 1 x ,则下列函数中为奇函数的是( )
1 x
A. f (x 1) 1 B. f (x 1) 1 C. f (x 1) 1 D. f (x 1) 1
6 1 1.(2021文科甲卷)设 f (x)是定义域为 R 的奇函数,且 f (1 x) f ( x) .若 f ( ) ,则
3 3
f (5) ( )
3
A 5 B 1 C 1 D 5. . . .
3 3 3 3
7.(2021新高考Ⅰ)已知函数 f (x) x3(a 2x 2 x )是偶函数,则 a ________.
8.(2021新高考Ⅱ)已知函数 f (x)的定义域为 R ( f (x)不恒为 0),f (x 2)为偶函数,f (2x 1)
为奇函数,则( )
A. f ( 1 ) 0 B. f ( 1) 0 C. f (2) 0 D. f (4) 0
2
2
9.(2020江苏)已知 y f (x)是奇函数,当 x 0时, f (x) x 3 ,则 f ( 8)的值是________.
10.(2021上海)以下哪个函数既是奇函数,又是减函数( )
A. y 3x B. y x3 C. y log3 x D. y 3
x
11.(2022上海春考)已知函数 y f (x)为定义域为 R的奇函数,其图像关于 x 1对称,且
当 x (0,1]时,f (x) lnx,若将方程 f (x) x 1的正实数根从小到大依次记为 x1,x2,x3 ,
, xn,则 lim(xn 1 xn ) ________.n
- 7 -
九.奇偶性与单调性的综合
1.(2021北京)函数 f (x) cos x cos2x是( )
A.奇函数,且最大值为 2 B.偶函数,且最大值为 2
C 9 9.奇函数,且最大值为 D.偶函数,且最大值为
8 8
2.(2021北京)设函数 f (x)的定义域为[0,1],则“ f (x)在区间[0,1]上单调递增”是“ f (x)
在区间 [0,1]上的最大值为 f (1)”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.(2021 上海春季)已知函数 y f (x) 的定义域为 R,下列是 f (x)无最大值的充分条件是
( )
A. f (x)为偶函数且关于点 (1,1)对称
B. f (x)为偶函数且关于直线 x 1对称
C. f (x)为奇函数且关于点 (1,1)对称
D. f (x)为奇函数且关于直线 x 1对称
4.(2020海南)若定义在 R 的奇函数 f (x)在 ( , 0)单调递减,且 f (2) 0 ,则满足 xf (x 1) 0
的 x的取值范围是( )
A. [ 1,1] [3, ) B. [ 3, 1] [0,1]
C. [ 1, 0] [1, ) D. [ 1, 0] [1,3]
5.(2020新课标Ⅱ理)设函数 f (x) ln | 2x 1| ln | 2x 1|,则 f (x) ( )
A 1.是偶函数,且在 ( , ) 单调递增
2
B 1 1.是奇函数,且在 ( , )单调递减
2 2
C 1.是偶函数,且在 ( , )单调递增
2
D 1.是奇函数,且在 ( , )单调递减
2
十.指对数函数的图象与性质
1.(2022上海) f (x) log3 (a x) log3 (6 x).
- 8 -
(1)若将函数 f (x)图像向下移m(m 0)后,图像经过 (3,0), (5,0),求实数 a,m的值.
(2)若 a 3且 a 0,求解不等式 f (x) f (6 x).
2. (2022 a浙江)已知 2 5,log8 3 b,则 4a 3b ( )
25 5
A. 25 B. 5 C. D.
9 3
3.(2020 a b新课标Ⅰ理)若 2 log2 a 4 2log4 b,则( )
A. a 2b B. a 2b C. a b2 D. a b2
十一、指数函数的实际应用
1.(2020新课标Ⅲ) Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据
公布数据建立了某地区新冠肺炎累计确诊病例数 I (t)(t 的单位:天 )的 Logistic模型:
I (t) K * ,其中 K为最大确诊病例数.当 I(t ) 0.95K时,标志着已初步遏制疫情,
1 e 0.23(t 53)
则 t * 约为( ) (ln19 3)
A.60 B.63 C.66 D.69
十二、指对大小的比较
1. (2022全国甲卷文)已知9m 10,a 10m 11,b 8m 9,则( )
A. a 0 b B. a b 0
C. b a 0 D. b 0 a
2.(2021 1新高考Ⅱ)已知 a log5 2, b log8 3, c ,则下列判断正确的是( )2
A. c b a B.b a c C. a c b D. a b c
3.(2021天津)若 2a 5b 10 1 1,则 ( )
a b
A. 1 B. lg7 C.1 D. log710
4.(2021天津)设 a log2 0.3, b log 1 0.4, c 0.4
0.3,则三者大小关系为( )
2
A. a b c B. c a b C.b c a D. a c b
- 9 -
5.(2020天津)设 a 30.7 b (1, ) 0.8, c log0.7 0.8,则 a, b, c的大小关系为( )3
A. a b c B.b a c C.b c a D. c a b
6.(2020新课标Ⅲ)已知 55 84,134 85 .设 a log 5 3 , b log8 5, c log13 8,则( )
A. a b c B. b a c C. b c a D. c a b
十三、函数值域
1.(2022上海)设函数 f (x)满足 f (x) f ( 1 ),定义域为 D [0, ),值域为 A,若集
x 1
合{y | y f (x), x [0, a]}可取得 A中所有值,则参数 a的取值范围为________.
2.(2021上海)已知 x1,x2 R,若对任意的 x2 x1 S , f (x2 ) f (x1) S,则有定义: f (x)
是在 S关联的.
(1)判断和证明 f (x) 2x 1是否在 [0, )关联?是否有 [0,1]关联?
(2)若 f (x)是在{3}关联的, f (x)在 x [0,3)时, f (x) x2 2x,求解不等式:2 f (x) 3.
(3)证明: f (x)是{1}关联的,且是在 [0, )关联的,当且仅当“ f (x)在 [1,2]是关联的”.
十四、函数的实际应用
1. (2022北京)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制
冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与 T和
lgP的关系,其中 T表示温度,单位是 K;P表示压强,单位是 bar.下列结论中正确的是
( )
- 10 -
A. 当T 220, P 1026时,二氧化碳处于液态
B. 当T 270, P 128时,二氧化碳处于气态
C. 当T 300, P 9987时,二氧化碳处于超临界状态
D. 当T 360, P 729时,二氧化碳处于超临界状态
2.(2021甲卷)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五
分记录法和小数记录法记录视力数据,五分记录法的数据 L和小数记录法的数据V 满足
L 5 lgV .已知某同学视力的五分记录法的数据为 4.9,则其视力的小数记录法的数据约
为( ) (1010 1.259)
A.1.5 B.1.2 C.0.8 D.0.6
十五、函数求值
1
1. (2022北京)己知函数 f (x) x ,则对任意实数 x,有( )1 2
A. f (- x)+ f (x) = 0 B. f ( x) f (x) 0
C. f ( x) f (x) 1 D. f ( x) f (x) 1
3
2. (2022全国乙卷理)已知函数 f (x), g(x)的定义域均为 R,且
f (x) g(2 x) 5, g(x) f (x 4) 7.若 y g(x)的图像关于直线 x 2对称,
22
g(2) 4,则 f (k ) ( )
k 1
A. 21 B. 22 C. 23 D. 24
- 11 -
2020-2022 函数高考题分类合集解析
一.反函数(上海)
1.【解答】函数 f (x) x3的反函数为 f 1(x),
整理得 f 1(x) 3 x;
所以 f 1(27) 3.
故答案为:3.
2.【解答】选项 A:因为函数是二次函数,属于二对一的映射,
根据函数的定义可得函数不存在反函数, A错误,
选项 B :因为函数是三角函数,有周期性和对称性,属于多对一的映射,
根据函数的定义可得函数不存在反函数, B 错误,
选项C :因为函数的单调递增的指数函数,属于一一映射,所以函数存在反函数,C 正确,
选项 D:因为函数是常数函数,属于多对一的映射,所以函数不存在反函数,D错误,
故选:C .
3 f (x) 3.【解答】因为 2,
x
令 f (x) 1 3,即 2 1,解得 x 3,
x
f 1故 (1) 3 .
故答案为: 3.
4 3.【解答】由 y f (x) x ,得 x 3 y ,
把 x 3 1与 y 互换,可得 f (x) x 的反函数为 f (x) 3 x.
故答案为: 3 x .
二.具体函数定义域
- 12 -
1
1.【解答】 y x 2 1 ,定义域为{x | x 0},
x
y x 1 1 ,定义域为{x | x 0},
x
1
y x 3 3 x ,定义域为 R,
1
y x 2 x ,定义域为{x | x 0}.
1
定义域为 R 的是 y x 3 .
故选:C.
1 1 x 0
2.【解答】因为 f x 1 x,所以 ,解得 x 1且 x 0,x x 0
故函数的定义域为 ,0 0,1 ;
故答案为: ,0 0,1
x 1 0
3.【解答】要使函数有意义,则 ,
x 0
x 1
所以 ,所以 x 0 ,
x 0
所以函数的定义域为{x | x 0},
故答案为:{x | x 0}.
三.函数的零点与方程根的关系
1.【解答】 f (x)在区间 (0, )内恰有 6个零点
又 二次函数最多有两个零点,
当 x a时, f (x) 0至少有四个根,
f (x) cos(2 x 2 a) cos[2 (x a)],
令 f (x) 0,即 2 (x a) k k Z ,
2
- 13 -
x k 1 a,
2 4
又 x (0, ),
0 k 1 a a 2a 1 1 ,即 k ,
2 4 2 2
①当 x a时, 5 2a 1 7 9 4, f (x)有 4个零点,即 a ,
2 4 4
6 2a 1 5, f (x) 5 9 a 11有 个零点,即 ,
2 4 4
7 2a 1 6 f (x) 6 11 a 13 , 有 个零点,即 ,
2 4 4
②当 x a时, f (x) x2 2(a 1)x a2 5,
△ b2 4ac 4(a 1)2 4(a2 5) 8a 16 0,解得 a 2,
当 a 2时,△ 0, f (x)无零点,
当 a 2时,△ 0, f (x)有 1个零点,
当 a 2时, f (a) a2 2a(a 1) a2 5 2a 5,
f (x)的对称轴 x a 1,即 f (a)在对称轴的左边,
5
当 2a 5 0时,即 2 a , f (x)有两个零点,
2
5
当 2a 5 0时,即 a , f (x)有 1个零点,
2
综合①②可得,若函数 f (x)在区间 (0, )内恰有 6个零点,则需满足:
7 a 9 9 a 11 11 13 4 4 4 4 a
或 或 4 4 ,
2 5 a a 5 或a 2 a 2 2 2
a (2 9解得 , ] (5 11, ].
4 2 4
故选: A.
2.【解答】函数 f (x) | lg x | kx 2的零点的个数可转化为函数 y | lg x |与直线 y kx 2的
交点的个数;
作函数 y | lg x |与直线 y kx 2的图象如右图,
若 k 0 ,则函数 y | lg x |与直线 y kx 2的图象在 (0,1)与 (1, )上各有一个交点,如直线
l1,则 f (x)有两个零点,故(1)正确;
- 14 -
当 k 2 时,当 x (0,1]时, f (x) lg x 2x 2,
f (10 2 ) 2 1 1 2 0, f (10 1) 1 2 0,
50 5
故 f (x)在 (10 2 10 1, )上至少有一个零点,
又 f (1) 0 ,结合图象知, f (x)在 (0,1]上有两个零点,
即 y | lg x |与 y 2x 2有两个不同的交点,故当直线绕点 (0, 2)顺时针旋转时,
存在直线 y kx 2与函数 y | lg x |与直线的图象相切,即 f (x)有一个零点,如直线 l2 ,故(2)
正确;
当 k 0 时,函数 y | lg x |与直线 y kx 2的图象至多有两个交点,故(3)不正确;
当 k 0 且 k足够小时,函数 y | lg x |与直线 y kx 2的图象在 (0,1)与 (1, )上分别有 1个、
2个交点,如直线 l3,故(4)正确;
故答案为:(1)(2)(4).
3.【解答】若函数 g(x) f (x) | kx2 2x | (k R)恰有 4个零点,
则 f (x) | kx2 2x |有四个根,
即 y f (x)与 y h(x) | kx2 2x |有四个交点,
当 k 0时, y f (x)与 y | 2x | 2 | x |图象如下:
- 15 -
两图象只有两个交点,不符合题意,
当 k 0时, y | kx2 2x | 2与 x轴交于两点 x1 0, x2 (x2 x1)k
图象如图所示,
1 1
当 x 时,函数 y | kx2 2x |的函数值为 ,
k k
x 1 1当 时,函数 y x的函数值为 ,
k k
所以两图象有 4个交点,符合题意,
当 k 0时,
y | kx2 2x | 2与 x轴交于两点 x1 0, x2 (x x )k 2 1
在 [0 2, )内两函数图象有两个交点,所以若有四个交点,
k
只需 y x3与 y kx2 2x (2在 , )还有两个交点,即可,
k
即 x3 kx2 2 2x在 ( , )还有两个根,
k
- 16 -
k x 2 (2即 在 , )还有两个根,
x k
函数 y x 2 2 2 ,(当且仅当 x 2 ,即 x 2 时,取等号),
x x
2
所以 0 2,且 k 2 2 ,
k
所以 k 2 2 ,
综上所述, k的取值范围为 ( , 0) (2 2 , ).
故选: D.
4.【解答】根据条件(1)可得 f (0) 0或 f (1) 1,
又因为关于 x的方程 f (x) a无实数解,所以 a 0或 1,
故 a ( , 0) (0,1) (1, ),
故答案为: ( , 0) (0,1) (1, ).
四.分段函数
1 , x 0
1.【解答】若 a 0时, f (x) ,∴ f (x) 0;
(x 2)
2 , x 0 min
若 a 0时,当 x a时, f (x) ax 1单调递增,当 x 时, f (x) ,故 f (x)没
- 17 -
有最小值,不符合题目要求;
若 a 0时,
当 x a时, f (x) ax 1单调递减, f (x) f (a) a2 1,
0 (0 a 2)
当 x a时, f (x)min {(a 2)2 (a 2)
∴ a2 1 0或 a2 1 (a 2)2,
解得0 a 1,
综上可得0 a 1;
故答案为:0(答案不唯一),1
2 7
2. 1 1 7【解答】由已知 f ( ) 2 , f ( )
7 4 37
1 ,
2 2 4 4 4 7 28
1 37
所以 f f ( ) , 2 28
当 x 1时,由1 f (x) 3可得1 x2 2 3,所以 1 x 1,
1
当 x 1时,由1 f (x) 3可得1 x 1 3,所以1 x 2 3,x
1 f (x) 3等价于 1 x 2 3,所以[a,b] [ 1,2 3],
所以b a的最大值为3 3 .
37
故答案为: ,
28 3 3
.
2
3 x 4, x 2.【解答】因为函数 f (x) ,
| x 3 | a, x 2
所以 f ( 6) ( 6)2 4 2,
则 f ( f ( 6)) f (2) | 2 3 | a 3,解得 a 2.
故答案为:2.
4.【解答】(1)按实际情况而言,交通流量 v随着道路密度 x的增大而减小,
- 18 -
故 v f (x)是单调递减函数,
所以 k 0,
当 40 x 80时, v最大为 85,
80
于是只需令100 135 (1) x 95 x 80,解得 ,
3 3
80
故道路密度 x的取值范围为 (0, ).
3
(2)把 x 80, v 50代入 v f (x) k (x 40) 85中,
7
得 50 k 40 85,解得 k .
8
80
100x 135 (
1
) x x,0 x 40
q vx 3 ,
7
(x 40)x 85x, 40 x 80 8
80
①当 0 x 40时, v 100 135 (1 ) x 100,
3
q vx 100 40 4000.
②当 40 x 80 7时, q是关于 x的二次函数, q x2 120x,
8
x 480 q 7 (480)2 120 480 28800对称轴为 ,此时 有最大值,为 4000.
7 8 7 7 7
综上所述,车辆密度 q 28800的最大值为 .
7
五.函数的图象与图象的变换
1. x
3 x
【解答】设 f x ,则 f 1 0,故排除 B;
x2 1
h x 2x cos x π设 2 ,当 x x 1
0, 时,0 cos x 1,
2
所以 h x 2x cos x 2x 2 2 1,故排除 C;x 1 x 1
g x 2sin x 2sin 3设
x2
,则 g 3 0,故排除 D.
1 10
故选:A.
2. x x【解答】令 f x 3 3 cos x, x ,
,
2 2
- 19 -
则 f x 3 x 3x cos x 3x 3 x cos x f x ,
所以 f x 为奇函数,排除 BD;
x 0, 又当 x 时,3 3 x 0,cos x 0,所以 f x 0,排除 C.
2
故选:A.
3 f (x) ln | x |.【解答】根据题意, 2 ,其定义域为{x | x 0},x 2
有 f ( x) ln | x | 2 f (x),是偶函数,排除 AC,x 2
在区间 (0,1)上, ln | x | ln x 0,必有 f (x) 0,排除D,
故选: B.
4.【解答】 y f (x) x cos x sin x,
则 f ( x) xcos x sin x f (x),
f (x)为奇函数,函数图象关于原点对称,故排除C ,D,
当 x 时, y f ( ) cos sin 0 ,故排除 B,
故选: A.
5 4x.【解答】函数 y 2 的定义域为实数集 R,关于原点对称,x 1
4x 4x
函数 y f (x) 2 ,则 f ( x) 2 f (x),则函数 y f (x)为奇函数,故排除C ,x 1 x 1
D,
当 x 0时, y f (x) 0,故排除 B,
故选: A.
6.【解答】设甲企业的污水排放量W 与时间 t的关系为W f (t),乙企业的污水排放量W 与
时间 t的关系为W g(t).
f (t ) f (t )
对于①,在 [t1, t2 ]这段时间内,甲企业的污水治理能力为
2 1 ,
t2 t1
g(t ) g(t )
乙企业的污水治理能力为 2 1 .
t2 t1
- 20 -
f (t2 ) f (t1) g(t2 ) g(t )由图可知, f (t1 ) f (t
1
2 ) g (t1 ) g (t2 ), ,t2 t1 t2 t1
即甲企业的污水治理能力比乙企业强,故①正确;
对于②,由图可知, f (t)在 t2 时刻的切线的斜率小于 g (t)在 t2 时刻的切线的斜率,但两切
线斜率均为负值,
在 t2 时刻,甲企业的污水治理能力比乙企业强,故②正确;
对于③,在 t3时刻,甲,乙两企业的污水排放都小于污水达标排放量,
在 t3时刻,甲,乙两企业的污水排放都已达标,故③正确;
对于④,由图可知,甲企业在 [0, t1],[t1, t2 ],[t2, t3 ]这三段时间中,在 [t1, t2 ]的污水
治理能力最强,
故④错误.
正确结论的序号是①②③.
故答案为:①②③.
六.函数单调性的性质与判断
1.【解答】(1) f (x) 2x , t 1, g(x)为 f (x)做 变换后的结果, g(x) 2,
g(x) f (x) f (x 1) 2x 2x 1 2x 1 2,
解得 x 2.
(2) f (x) x2 , h(x)为 f (x)做 变换后的结果, f (x) h(x) ,
x2 | (x t)2 x2 | | 2tx t 2 |,
t
当 x 时, f (x) h(x)恒成立;
2
t
当 x 时, 2tx t 2 x2 ,
2
解得 x (1 2)t,或 x (1 2)t,
综上,不等式: f (x) h(x)的解集为 ( , (1 2)t] [(1 2)t, ).
(3)证明: f (x)先做 变换后得到 u(x),u(x)再做 变换后得到 h1(x),
u(x) f (x) f (x t) , h1(x) | f (x t) f (x) [ f (x) f (x t)] |,
- 21 -
f (x)先做 变换后得到 v(x), v(x)再做 变换后得到 h2 (x),
v(x) | f (x t) f (x) |, h2 (x) | f (x t) f (x) | | f (x) f (x t) |,
h1(x) h2 (x), f (x)在 ( ,0)上单调递增,
| f (x t) f (x) [ f (x) f (x t)] | | f (x t) f (x) | | f (x) f (x t) | ,
f (x t) f (t) f (t) f (t 1)
t 0 , f (x t) f (x) 0 ,
f (x) f (x t)
函数 f (x)在 R 上单调递增.
2.【解答】由一次函数性质可知 f (x) x在 R 上是减函数,不符合题意;
2
由指数函数性质可知 f (x) ( )x在 R 上是减函数,不符合题意;
3
由二次函数的性质可知 f (x) x2在 R 上不单调,不符合题意;
根据幂函数性质可知 f (x) 3 x 在 R 上单调递增,符合题意.
故选: D.
3.【解答】(1)当 a 1时, f (x) | x 1| 1 x ,
由 | x 1| 1 0,得 | x 1| 1,解得 x 2或 x 0.
函数的定义域为 ( , 2] [0, );
(2) f (ax) | ax a | a ax ,
f (ax) a | ax a | a ax a ,
设 ax a t 0, t a t有两个不同实数根,整理得 a t t2 , t 0,
a (t 1)2 1 1 , t 0,当且仅当 0 a 时,方程有 2个不同实数根,
2 4 4
又 a 0, a的取值范围是 (0, 1);
4
(3)当 x a时, f (x) | x a | a x x x ( x 1)2 1 1 ,在 [ , )上单调递减,
2 4 4
- 22 -
a 1此时需要满足 ,即 a 1 ,函数 f (x)在[ a, )上递减;
4 4
当 x a时, f (x) | x a | a x x 2a x,在 ( , 2a]上递减,
a 1 0, 2a a 1 0,即当 a 时,函数 f (x)在 ( , a)上递减.
4 4
1
综上,当 a ( , ]时,函数 f (x)在定义域 R 上连续,且单调递减.
4
4.【解答】对于命题 q1:当 f (x)单调递减且 f (x) 0恒成立时,
当 a 0时,此时 x a x,
又因为 f (x)单调递减,
所以 f (x a) f (x)
又因为 f (x) 0恒成立时,
所以 f (x) f (x) f (a),
所以 f (x a) f (x) f (a),
所以命题 q1 命题 p,
对于命题 q2:当 f (x)单调递增,存在 x0 0使得 f (x0 ) 0,
当 a x0 0时,此时 x a x, f (a) f (x0 ) 0,
又因为 f (x)单调递增,
所以 f (x a) f (x),
所以 f (x a) f (x) f (a),
所以命题 p2 命题 p,
所以 q1, q2都是 p的充分条件,
故选:C.
5.【解答】由 2x 2y 3 x 3 y ,可得 2x 3 x 2y 3 y ,
令 f (x) 2x 3 x,则 f (x)在 R 上单调递增,且 f (x) f (y),
所以 x y ,即 y x 0,由于 y x 1 1,
故 ln(y x 1) ln1 0.
- 23 -
七.复合函数的单调性
1.【解答】由 x2 4x 5 0,得 x 1或 x 5 .
令 t x2 4x 5,
外层函数 y lg t是其定义域内的增函数,
要使函数 f (x) lg(x2 4x 5)在 (a, )上单调递增,
则需内层函数 t x2 4x 5在 (a, )上单调递增且恒大于 0,
则 (a, ) (5, ),即 a 5.
a的取值范围是 [5, ).
故选: D.
八.函数奇偶性的性质与判断
1. 【解答】因为函数 f x ln a 1 b为奇函数,所以其定义域关于原点对称.
1 x
a 1 a 1 1由 0可得, 1 x a 1 ax 0,所以 x 1,解得:a ,即函
1 x a 2
数的定义域为 , 1 1,1 1, ,再由 f 0 0可得,b ln 2.即
f x ln 1 1 ln 2 ln 1 x ,在定义域内满足 f x f x ,符合题意.
2 1 x 1 x
1
故答案为: ; ln 2.
2
a2x 1 x 0
2 .【解答】 函数 f (x) x a x 0,为奇函数, f ( x) f (x),
0 x 0
f ( 1) f (1), a2 1 (a 1),即 a(a 1) 0,求得 a 0或 a 1.
1, x 0
当 a 0时, f (x) 0, x 0 ,不是奇函数,故 a 0;
x, x 0
- 24 -
x 1, x 0
当 a 1时, f (x) 0, x 0 ,是奇函数,故满足条件,
x 1, x 0
综上, a 1,
故答案为:1.
3.【解答】因为 f x y f x y f x f y ,令 x 1, y 0可得,
2 f 1 f 1 f 0 ,所以 f 0 2,令 x 0可得, f y f y 2 f y ,即
f y f y ,所以函数 f x 为偶函数,令 y 1得,
f x 1 f x 1 f x f 1 f x ,即有 f x 2 f x f x 1 ,从而可知
f x 2 f x 1 , f x 1 f x 4 ,故 f x 2 f x 4 ,即
f x f x 6 ,所以函数 f x 的一个周期为6.
因为 f 2 f 1 f 0 1 2 1, f 3 f 2 f 1 1 1 2,
f 4 f 2 f 2 1, f 5 f 1 f 1 1, f 6 f 0 2,所以
一个周期内的 f 1 f 2 f 6 0.由于 22除以 6余 4,
22
所以 f k f 1 f 2 f 3 f 4 1 1 2 1 3.
k 1
故选:A.
4.【解答】 f (x 1)为奇函数, f (1) 0,且 f (x 1) f ( x 1),
f (x 2)偶函数, f (x 2) f ( x 2),
f [(x 1) 1] f [ (x 1) 1] f ( x) ,即 f (x 2) f ( x),
f ( x 2) f (x 2) f ( x).
令 t x,则 f (t 2) f (t) ,
f (t 4) f (t 2) f (t), f (x 4) f (x).
当 x [1, 2]时, f (x) ax2 b.
f (0) f ( 1 1) f (2) 4a b,
- 25 -
f (3) f (1 2) f ( 1 2) f (1) a b,
又 f (0) f (3) 6, 3a 6,解得 a 2,
f (1) a b 0, b a 2,
当 x [1, 2]时, f (x) 2x2 2,
f (9) 1 3 9 5 f ( ) f ( ) ( 2 2) .
2 2 2 4 2
故选: D.
5.【解答】因为 f (x) 1 x (x 1) 2 2 1 ,
1 x 1 x x 1
所以函数 f (x)的对称中心为 ( 1, 1),
所以将函数 f (x)向右平移一个单位,向上平移一个单位,
得到函数 y f (x 1) 1,该函数的对称中心为 (0,0),
故函数 y f (x 1) 1为奇函数.
故选: B.
6.【解答】由题意得 f ( x) f (x),
又 f (1 x) f ( x) f (x) ,
所以 f (2 x) f (x),
又 f ( 1 1 ) ,
3 3
则 f (5) f (2 1 ) f ( 1 ) 1 .
3 3 3 3
故选:C.
7.【解答】函数 f (x) x3(a 2x 2 x )是偶函数,
y x3为 R 上的奇函数,
故 y a 2x 2 x也为 R 上的奇函数,
所以 y | a 20x 0 2
0 a 1 0,
所以 a 1.
8.【解答】 函数 f (x 2)为偶函数,
- 26 -
f (2 x) f (2 x),
f (2x 1)为奇函数,
f (1 2x) f (2x 1),
用 x替换上式中 2x 1,得 f (2 x) f (x),
f (2 x) f (x), f (4 x) f (2 x) f (x) ,即 f (x) f (x 4),
故函数 f (x)是以 4为周期的周期函数,
f (2x 1)为奇函数,
f (1 2x) f (2x 1),即 f (2x 1) f ( 2x 1) 0 ,
用 x替换上式中 2x 1,可得, f (x) f (2 x) 0,
f (x)关于 (1,0)对称,
又 f (1) 0,
f ( 1) f (2 1) f ( 1) 0 .
故选: B.
9.【解答】 y f (x)是奇函数,可得 f ( x) f (x),
2 2
当 x 0时, f (x) x 3 ,可得 f (8) 83 4,
则 f ( 8) f (8) 4,
故答案为: 4.
10.【解答】 y 3x在 R 上单调递减且为奇函数, A符合题意;
因为 y x3在 R 上是增函数, B不符合题意;
y log3 x, y 3
x 为非奇非偶函数,C 不符合题意;
故选: A.
11.【解答】 函数 y f (x)为定义域为 R 的奇函数,其图像关于 x 1对称,且当 x (0,1]
时, f (x) lnx,
f (x)是周期为 4的周期函数,图象如图:
- 27 -
将方程 f (x) x 1的正实数根从小到大依次记为 x1, x2, x3 , , xn,
则 lim(xn 1 xn )的几何意义是两条渐近线之间的距离 2,n
lim(x x ) 2.
n n 1 n
故答案为:2.
九.奇偶性与单调性的综合
1.【解答】因为 f (x) cos x cos2x cos x (2cos2 x 1) 2cos2 x cos x 1,
因为 f ( x) 2cos2 ( x) cos( x) 1 2cos2 x cos x 1 f (x),
故函数 f (x)为偶函数,
令 t cos x,则 t [ 1,1],
故 f (t) 2t2 t 1是开口向下的二次函数,
t 1 1 f (t) 1 1 1 9所以当 时, 取得最大值 f ( ) 2 ( )2 1 ,
2 ( 2) 4 4 4 4 8
9
故函数的最大值为 .
8
综上所述,函数 f (x) 9是偶函数,有最大值 .
8
故选: D.
2.【解答】若函数 f (x)在 [0,1]上单调递增,
则函数 f (x)在 [0,1]上的最大值为 f (1),
若 f (x) (x 1 )2 ,则函数 f (x)在[0,1]上的最大值为 f (1),
3
但函数 f (x)在 [0,1]上不单调,
- 28 -
故选: A.
3.【解答】根据题意,依次判断选项:
对于 A, f (x) cos x 1, f (x)为偶函数,且关于点 (1,1)对称,存在最大值, A错误,
2
对于 B, f (x) cos( x) , f (x)为偶函数且关于直线 x 1对称,存在最大值, B错误,
对于C,假设 f (x)有最大值,设其最大值为M ,其最高点的坐标为 (a,M ),
f (x)为奇函数,其图象关于原点对称,则 f (x)的图象存在最低点 ( a, M ),
又由 f (x)的图象关于点 (1,1)对称,则 ( a, M )关于点 (1,1)对称的点为 (2 a, 2 M ),
与最大值为M 相矛盾,则此时 f (x)无最大值,C 正确,
对于 D, f (x) sin x , f (x)为奇函数且关于直线 x 1对称, D错误,
2
故选:C.
4.【解答】 定义在 R 的奇函数 f (x)在 ( , 0)单调递减,且 f (2) 0 , f (x)的大致图象如
图:
f (x)在 (0, )上单调递减,且 f ( 2) 0;
故 f ( 1) 0;
当 x 0 时,不等式 xf (x 1) 0成立,
当 x 1时,不等式 xf (x 1) 0成立,
当 x 1 2或 x 1 2 时,即 x 3或 x 1时,不等式 xf (x 1) 0成立,
当 x 0 时,不等式 xf (x 1) 0等价为 f (x 1) 0,
x 0
此时 ,此时1 x 3,
0 x 1 2
当 x 0 时,不等式 xf (x 1) 0等价为 f (x 1) 0,
- 29 -
x 0
即 ,得 1 x 0,
2 x 1 0
综上 1 x 0或1 x 3,
即实数 x的取值范围是 [ 1, 0] [1,3],
故选: D.
2x 1 0
5 1.【解答】由 ,得 x .
2x 1 0 2
又 f ( x) ln | 2x 1| ln | 2x 1| (ln | 2x 1| ln | 2x 1|) f (x),
f (x)为奇函数;
f (x) ln | 2x 1| ln | 2x 1| ln | 2x 1| ln | 2x 1由 |,
| 2x 1| 2x 1
2x 1 2x 1 2 1 2 2 1 1 1 .
2x 1 2x 1 2x 1 2(x 1) x 1
2 2
t | 2x 1可得内层函数 |的图象如图,
2x 1
1 1 1
在 ( , )上单调递减,在 ( , )上单调递增,
2 2 2
1
则 ( , ) 上单调递减.
2
又对数式 y ln t是定义域内的增函数,
f (x) ( , 1由复合函数的单调性可得, 在 )上单调递减.
2
故选: D.
- 30 -
十.指对数函数的图象与性质
1.【解答】(1)因为函数 f (x) log3 (a x) log3 (6 x),
将函数 f (x)图像向下移m(m 0)后,得 y f (x) m log3 (a x) log3 (6 x) m的图像,
由函数图像经过点 (3,0)和 (5,0),
log3(3 a) 1 m 0
所以 ,
log3(5 a) 0 m 0
解得 a 2,m 1.
(2) a 3且 a 0时,不等式 f (x) f (6 x)可化为
log3 (a x) log3 (6 x) log3 (a 6 x) log3 x,
a x 0
6 x 0
等价于 a 6 x 0 ,
x 0
(a x)(6 x) x(a 6 x)
x a
x 6
解得 x a 6 ,
x 0
a(x 3) 0
当 3 a 0时, 0 a 3, 3 a 6 6,解不等式得 a x 3,
当 a 0时, a 0, a 6 6,解不等式得 3 x 6;
综上知, 3 a 0时,不等式 f (x) f (6 x)的解集是 ( a, 3],
a 0时,不等式 f (x) f (6 x)的解集是 [3, 6).
2.【解答】因为2a 5,b log 3
1
log 3,即 23b8 2 3,所以3
a
a 3b 4 2a
2
524 25
43b
3b 2 32
.
2 9
- 31 -
故选:C.
3 a b.【解答】因为 2 log2 a 4 2log4 b 2
2b log2 b;
22b log b 22b 2b因为 2 log2 2b 2 log2 b 1,
2a log a 22b所以 2 log2 2b,
令 f (x) 2x log2 x,由指对数函数的单调性可得 f (x)在 (0, )内单调递增;
且 f (a) f (2b) a 2b;
故选: B .
十一、指数函数的实际应用
K
1 * 1.【解答】由已知可得 * 0.95K,解得 0.23(t 53) ,
1 e 0.23(t 53)
e
19
0.23(t*两边取对数有 53) ln19,
解得 t* 66,
故选:C .
十二、指对大小的比较
lg10
1.【解答】由9m 10可得m log910 1,而lg9
2 2 lg10 lg11
lg9lg11 lg9 lg11 lg99 1 lg10
2
,所以 ,即m lg11,所
2 2 lg9 lg10
以 a 10m 11 10lg11 11 0.
lg8 lg10 2 lg80 2 2 lg9 lg10
又 lg8lg10 lg9 ,所以 ,即 log2 2 lg8 lg9 8
9 m,
所以b 8m 9 8log8 9 9 0.综上, a 0 b.
- 32 -
故选:A.
1 1 12 log 2 log 5 2 log 3 log 8 2 1.【解答】 5 5 , 8 8 ,2 2
a c b.
故选:C.
3.【解答】 2a 5b 10, a log210,b log510,
1 1 1 1
log10 2 log10 5 lg10 1,a b log210 log510
故选:C.
4.【解答】 log2 0.3 log21 0, a 0,
log1 0.4 log1 0.5 1, b 1,
2 2
0 0.40.3 0.40 1, 0 c 1,
a c b,
故选: D.
5.【解答】 a 30.7 , b (1 ) 0.8 30.8,
3
则 b a 1,
log0.7 0.8 log0.7 0.7 1,
c a b,
故选: D.
6 3 3.【解答】由 log5 5 log 8,4 4 8
3 3
log5 54 log 3,而 log 845 8 log8 5
log5 3 log8 5,
即 a b ;
55 84 , 5 4 log5 8, log 5 8 1.25, b log8 5 0.8;
134 85 , 4 5 log13 8, c log13 8 0.8, c b ,
- 33 -
综上, c b a.
故选: A.
十三、函数值域
1 1.【解答】令 x 得,
x 1
x 5 1 5 1 或 x (舍去);
2 2
当 x 5 1 时,
2
1 1 5 1
,
x 1 5 1 2
1
2
x 5 1故对任意 ,
2
x [0 5 1都存在 0 , ]
1
, x ,
2 x 1 0
故 f (x) f (x0 ),
0 x 5 1而当 时,
2
1 1 5 1
,
x 1 5 1 2
1
2
故 A {y | y f (x) x [0 5 1, , ]},
2
故当 A {y | y f (x), x [0, a]}时,
[0 5 1, ] [0, a],
2
a 5 1故参数 的最小值为 ,
2
a [ 5 1故参数 的取值范围为 , ),
2
5 1
故答案为: [ , ).
2
2.【解答】(1) f (x)在 [0, )关联,在 [0,1]不关联,
任取 x1 x2 [0, ),则 f (x1) f (x2 ) 2(x1 x2 ) [0, ), f (x)在 [0, )关联;
- 34 -
取 x1 1, x2 0,则 x1 x2 1 [0,1],
f (x1) f (x2 ) 2(x1 x2 ) 2 [0,1], f (x)在 [0,1]不关联;
(2) f (x)在{3}关联, 对于任意 x1 x2 3,都有 f (x1) f (x2 ) 3,
对任意 x,都有 f (x 3) f (x) 3,
由 x [0, 3)时, f (x) x2 2x,得 f (x)在 x [0, 3)的值域为 [ 1, 3),
f (x)在 x [3, 6)的值域为 [2, 6),
2 f (x) 3仅在 x [0, 3)或 x [3, 6)上有解,
x [0, 3)时, f (x) x2 2x,令 2 x2 2x 3,解得 3 1 x 3,
x [3, 6)时, f (x) f (x 3) 3 x2 8x 18,令 2 x2 8x 18 3,解得 3 x 5,
不等式 2 f (x) 3的解为 [ 3 1, 5],
(3)证明:①先证明: f (x)是在{1}关联的,且是在 [0, )关联的 f (x)在 [1, 2]是关联
的,
由已知条件可得, f (x 1) f (x) 1,
f (x n) f (x) n, n Z ,
又 f (x)是在 [0, )关联的,
任意 x2 x1, f (x2 ) f (x1)成立,
若1 x2 x1 2,
x1 1 x2 x1 2,
f (x1 1) f (x2 ) f (x1 2),即 f (x1) 1 f (x2 ) f (x1) 2,
1 f (x2 ) f (x1) 2,
f (x)是[1, 2]关联,
②再证明: f (x)在 [1, 2]是关联的 f (x)是在{1}关联的,且是在[0, )关联的,
f (x)在[1, 2]是关联的, 任取 x1 x2 [1, 2],都有 f (x1) f (x2 ) [1, 2]成立,
即满足1 x1 x2 2,都有1 f (x1) f (x2 ) 2,
下面用反证法证明 f (x 1) f (x) 1,
- 35 -
若 f (x 1) f (x) 1,则 f (x 2) f (x) f (x 2) f (x 1) f (x 1) f (x) 2 ,与 f (x)在 [1,
2]是关联的矛盾,
若 f (x 1) f (x) 1,而 f (x)在 [1, 2]是关联的,则 f (x 1) f (x) 1,矛盾,
f (x 1) f (x) 1成立,即 f (x)是在{1}关联的,
再证明 f (x)是在 [0, )关联的,
任取 x1 x2 [n, )(n N ),则存在 n N ,使得任取 x1 x2 [n, n 1](n N ),
1 x1 (n 1) x2 2,
f [x1 (n 1)] f (x2 ) f (x1) (n 1) f (x2 ) [1, 2],
f (x1) f (x2 ) [n, n 1] [0, ),
f (x)是在 [0, )关联的;
综上所述, f (x)是{1}关联的,且是在[0, )关联的,当且仅当“ f (x)在 [1,2]是关联的”,
故得证.
十四、函数的实际应用
1.【解答】当T 220,P 1026时, lg P 3,此时二氧化碳处于固态,故 A错误.
当T 270, P 128时, 2 lg P 3,此时二氧化碳处于液态,故 B错误.
当T 300, P 9987时, lgP与 4非常接近,故此时二氧化碳处于固态,
另一方面,T 300时对应的是非超临界状态,故 C错误.
当T 360, P 729时,因 2 lg P 3 , 故此时二氧化碳处于超临界状态,故 D正确.
故选:D
2.【解答】在 L 5 lgV 中, L 4.9,所以 4.9 5 lgV ,即 lgV 0.1,
解得V 10 0.1 1 1 1
100.1
0.8 ,
1010 1.259
所以其视力的小数记录法的数据约为 0.8.
故选:C.
- 36 -
十五、函数求值
x
1. 【解答】 f x f x 1 1 2 1 1,故 A错误,C正确;
1 2 x 1 2x 1 2x 1 2x
x x
f x f x 1 1 2 1 2 1 2 1 ,不是常数,故 BD
1 2 x 1 2x 1 2x 1 2x 2x 1 2x 1
错误;
故选:C.
2.【解答】因为 y g(x)的图像关于直线 x 2对称,
所以 g 2 x g x 2 ,
因为 g(x) f (x 4) 7,所以 g(x 2) f (x 2) 7,即 g(x 2) 7 f (x 2),
因为 f (x) g(2 x) 5,所以 f (x) g(x 2) 5,
代入得 f (x) 7 f (x 2) 5,即 f (x) f (x 2) 2,
所以 f 3 f 5 f 21 2 5 10,
f 4 f 6 f 22 2 5 10 .
因为 f (x) g(2 x) 5,所以 f (0) g(2) 5,即 f 0 1,所以
f (2) 2 f 0 3 .
因为 g(x) f (x 4) 7,所以 g(x 4) f (x) 7,又因为 f (x) g(2 x) 5,
联立得, g 2 x g x 4 12,
所以 y g(x)的图像关于点 3,6 中心对称,因为函数 g(x)的定义域为 R,
所以 g 3 6
因为 f (x) g(x 2) 5,所以 f 1 5 g 3 1 .
所以
- 37 -
22
f (k) f 1 f 2 f 3 f 5 f 21 f 4 f 6 f 22 1 3 10 10 24
k 1
故选:D
- 38 -
一.反函数(上海)
1.(2022上海春考)设函数 f (x) x3的反函数为 f 1(x),则 f 1(27) ________.
2.(2021上海春季)下列函数中,在定义域内存在反函数的是( )
A. f (x) x2 B. f (x) sin x C. f (x) 2x D. f (x) 1
3.(2021 3 1上海)已知 f (x) 2,则 f (1) ________.
x
4.(2020 ) 3 1 1上海 已知函数 f (x) x , f (x)是 f (x)的反函数,则 f (x) ________, x R.
二.具体函数定义域
1.(2022上海春考)下列函数定义域为 R 的是( )
1 1 1
A. y x 2 B. y x 1 C. y x 3 D. y x 2
f (x) 12.(2022北京)函数 1 x 的定义域是________.
x
3.(2020北京)函数 f (x) 1 ln x的定义域是________.
x 1
三.函数的零点与方程根的关系
cos(2 x 2 a) x a
1.(2021天津)设 a R,函数 f (x) 2 ,若函数 f (x)在区间 (0, )
x 2(a 1)x a
2 5 x a
内恰有 6个零点,则 a的取值范围是( )
A (2 9 5 11 7. , ] ( , ] B. ( , 2] (5 11, ]
4 2 4 4 2 4
C. (2 9, ] [11 7 11,3) D. ( , 2) [ ,3)4 4 4 4
2.(2021北京)已知函数 f (x) | lg x | kx 2,给出下列四个结论:
(1)若 k 0 ,则 f (x)有 2个零点;
(2)存在负数 k,使得 f (x)恰有 1个零点;
- 1 -
(3)存在负数 k,使得 f (x)恰有 3个零点;
(4)存在正数 k,使得 f (x)恰有 3个零点.
其中所有正确结论的序号是________.
3
3 (2020 ) x , x 0,. 天津 已知函数 f (x) 若函数 g(x) f (x) | kx2 2x | (k R)恰有 4 个零
x, x 0
点,则 k的取值范围是( )
A. ( 1 , ) (2 2 , ) B. ( 1 , ) (0, 2 2)
2 2
C. ( , 0) (0, 2 2) D. ( , 0) (2 2 , )
4.(2020上海)设 a R,若存在定义域为 R 的函数 f (x)同时满足下列两个条件:
(1)对任意的 x0 R, f (x )的值为 x 或 x
2
0 0 0 ;
(2)关于 x的方程 f (x) a无实数解,
则 a的取值范围是________.
四.分段函数
ax 1, x a,
1. (2022北京)设函数 f x 2 若 f (x)存在最小值,则 a的一个取值为
x 2 , x a.
________;a的最大值为________.
x2 2, x 1,
1
2. (2022浙江)已知函数 f x 1 则 f f ________;若当 x [a,b]
x 1, x 1, 2 x
时,1 f (x) 3,则b a的最大值是________.
2
3 (2021 ) x 4, x 2,. 浙江 已知 a R,函数 f (x) 若 f ( f ( 6)) 3,则 a ________.
| x 3 | a, x 2
4.(2020上海)在研究某市交通情况时,道路密度是指该路段上一定时间内通过的车辆数除
以时间,车辆密度是该路段一定
q
时间内通过的车辆数除以该路段的长度,现定义交通流量为 v , x为道路密度, q为车
x
- 2 -
80
100 135 1 ( ) x ,0 x 40
辆密度,交通流量 v f (x) 3 .
k(x 40) 85,40 x 80
(1)若交通流量 v 95,求道路密度 x的取值范围;
(2)已知道路密度 x 80时,测得交通流量 v 50,求车辆密度 q的最大值.
五.函数的图象与图象的变换
1. (2022全国乙卷文)如图是下列四个函数中的某个函数在区间[ 3,3]的大致图像,则该函数
是( )
x3 3A. y 3x B.2 y
x x
x 1 x2 1
2x cos x 2sin x
C. y 2 D. y x 1 x2 1
2. (2022 x x全国甲卷)函数 y 3 3 cos x π在区间 ,
π
的图象大致为( ) 2 2
A. B.
- 3 -
C. D.
3.(2021 ) ln | x |天津 函数 f (x) 2 的图象大致为( )x 2
A. B.
C. D.
4.(2020浙江)函数 y x cos x sin x 在区间 [ , ]上的图象可能是( )
A. B.
C. D.
5.(2020 4x天津)函数 y 2 的图象大致为( )x 1
A. B.
- 4 -
C. D.
6.(2020北京)为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放
未达标的企业要限期整改.设企业的污水排放量W 与时间 t 的关系为W f (t) ,用
f (b) f (a)
的大小评价在 [a,b]这段时间内企业污水治理能力的强弱.已知整改期内,甲、
b a
乙两企业的污水排放量与时间的关系如图所示.
给出下列四个结论:
①在 [t1, t2 ]这段时间内,甲企业的污水治理能力比乙企业强;
②在 t2 时刻,甲企业的污水治理能力比乙企业强;
③在 t3时刻,甲,乙两企业的污水排放都已达标;
④甲企业在 [0, t1], [t1, t2 ], [t2, t3 ]这三段时间中,在 [0, t1]的污水治理能力最强.
其中所有正确结论的序号是________.
六.函数单调性的性质与判断
1.(2022 上海春考)已知函数 f (x)的定义域为 R,现有两种对 f (x)变换的操作: 变换:
f (x) f (x t); 变换: | f (x t) f (x) |,其中 t为大于 0的常数.
(1)设 f (x) 2x, t 1, g(x)为 f (x)做 变换后的结果,解方程: g(x) 2;
(2)设 f (x) x2, h(x)为 f (x)做 变换后的结果,解不等式: f (x) h(x) ;
(3)设 f (x)在 ( ,0)上单调递增,f (x)先做 变换后得到 u(x),u(x)再做 变换后得到 h1(x);
f (x)先做 变换后得到 v(x), v(x)再做 变换后得到 h2 (x).若 h1(x) h2 (x)恒成立,
证明:函数 f (x)在 R 上单调递增.
- 5 -
2.(2021甲卷文)下列函数中是增函数的为( )
A. f (x) x B. f (x) (2)x C. f (x) x2 D. f (x) 3 x
3
3.(2021上海春季)已知函数 f (x) | x a | a x.
(1)若 a 1,求函数的定义域;
(2)若 a 0,若 f (ax) a有 2个不同实数根,求 a的取值范围;
(3)是否存在实数 a,使得函数 f (x)在定义域内具有单调性?若存在,求出 a的取值范围.
4.(2020上海)命题 p:存在 a R 且 a 0,对于任意的 x R,使得 f (x a) f (x) f (a);
命题 q1 : f (x)单调递减且 f (x) 0恒成立;
命题 q2 : f (x)单调递增,存在 x0 0使得 f (x0 ) 0,
则下列说法正确的是( )
A.只有 q1是 p的充分条件 B.只有 q2是 p的充分条件
C. q1, q2都是 p的充分条件 D. q1, q2都不是 p的充分条件
5.(2020新课标Ⅱ理)若 2x 2y 3 x 3 y ,则( )
A. ln(y x 1) 0 B. ln(y x 1) 0
C. ln | x y | 0 D. ln | x y | 0
七.复合函数的单调性
1 2.(2020海南)已知函数 f (x) lg(x 4x 5)在 (a, )上单调递增,则a的取值范围
是( )
A. (2, ) B.[2, ) C. (5, ) D.[5, )
八.函数奇偶性的性质与判断
1
1. (2022全国乙卷文)若 f x ln a b是奇函数,则a ________,b ________.
1 x
- 6 -
a2x 1 x 0
2.(2022上海)若函数 f (x) x a x 0,为奇函数,求参数 a的值为________.
0 x 0
3. (2022新高考 II)已知函数 f (x)的定义域为 R,且
22
f (x y) f (x y) f (x) f ( y), f (1) 1,则 f (k) ( )
k 1
A. 3 B. 2 C. 0 D. 1
4.(2021甲卷)设函数 f (x)的定义域为 R, f (x 1)为奇函数, f (x 2)为偶函数,当 x [1,
2]时, f (x) ax2 b.若 f (0) f (3) 6 f (9 ,则 ) ( )
2
A 9. B 3 C 7 5. . D.
4 2 4 2
5.(2021乙卷)设函数 f (x) 1 x ,则下列函数中为奇函数的是( )
1 x
A. f (x 1) 1 B. f (x 1) 1 C. f (x 1) 1 D. f (x 1) 1
6 1 1.(2021文科甲卷)设 f (x)是定义域为 R 的奇函数,且 f (1 x) f ( x) .若 f ( ) ,则
3 3
f (5) ( )
3
A 5 B 1 C 1 D 5. . . .
3 3 3 3
7.(2021新高考Ⅰ)已知函数 f (x) x3(a 2x 2 x )是偶函数,则 a ________.
8.(2021新高考Ⅱ)已知函数 f (x)的定义域为 R ( f (x)不恒为 0),f (x 2)为偶函数,f (2x 1)
为奇函数,则( )
A. f ( 1 ) 0 B. f ( 1) 0 C. f (2) 0 D. f (4) 0
2
2
9.(2020江苏)已知 y f (x)是奇函数,当 x 0时, f (x) x 3 ,则 f ( 8)的值是________.
10.(2021上海)以下哪个函数既是奇函数,又是减函数( )
A. y 3x B. y x3 C. y log3 x D. y 3
x
11.(2022上海春考)已知函数 y f (x)为定义域为 R的奇函数,其图像关于 x 1对称,且
当 x (0,1]时,f (x) lnx,若将方程 f (x) x 1的正实数根从小到大依次记为 x1,x2,x3 ,
, xn,则 lim(xn 1 xn ) ________.n
- 7 -
九.奇偶性与单调性的综合
1.(2021北京)函数 f (x) cos x cos2x是( )
A.奇函数,且最大值为 2 B.偶函数,且最大值为 2
C 9 9.奇函数,且最大值为 D.偶函数,且最大值为
8 8
2.(2021北京)设函数 f (x)的定义域为[0,1],则“ f (x)在区间[0,1]上单调递增”是“ f (x)
在区间 [0,1]上的最大值为 f (1)”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.(2021 上海春季)已知函数 y f (x) 的定义域为 R,下列是 f (x)无最大值的充分条件是
( )
A. f (x)为偶函数且关于点 (1,1)对称
B. f (x)为偶函数且关于直线 x 1对称
C. f (x)为奇函数且关于点 (1,1)对称
D. f (x)为奇函数且关于直线 x 1对称
4.(2020海南)若定义在 R 的奇函数 f (x)在 ( , 0)单调递减,且 f (2) 0 ,则满足 xf (x 1) 0
的 x的取值范围是( )
A. [ 1,1] [3, ) B. [ 3, 1] [0,1]
C. [ 1, 0] [1, ) D. [ 1, 0] [1,3]
5.(2020新课标Ⅱ理)设函数 f (x) ln | 2x 1| ln | 2x 1|,则 f (x) ( )
A 1.是偶函数,且在 ( , ) 单调递增
2
B 1 1.是奇函数,且在 ( , )单调递减
2 2
C 1.是偶函数,且在 ( , )单调递增
2
D 1.是奇函数,且在 ( , )单调递减
2
十.指对数函数的图象与性质
1.(2022上海) f (x) log3 (a x) log3 (6 x).
- 8 -
(1)若将函数 f (x)图像向下移m(m 0)后,图像经过 (3,0), (5,0),求实数 a,m的值.
(2)若 a 3且 a 0,求解不等式 f (x) f (6 x).
2. (2022 a浙江)已知 2 5,log8 3 b,则 4a 3b ( )
25 5
A. 25 B. 5 C. D.
9 3
3.(2020 a b新课标Ⅰ理)若 2 log2 a 4 2log4 b,则( )
A. a 2b B. a 2b C. a b2 D. a b2
十一、指数函数的实际应用
1.(2020新课标Ⅲ) Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据
公布数据建立了某地区新冠肺炎累计确诊病例数 I (t)(t 的单位:天 )的 Logistic模型:
I (t) K * ,其中 K为最大确诊病例数.当 I(t ) 0.95K时,标志着已初步遏制疫情,
1 e 0.23(t 53)
则 t * 约为( ) (ln19 3)
A.60 B.63 C.66 D.69
十二、指对大小的比较
1. (2022全国甲卷文)已知9m 10,a 10m 11,b 8m 9,则( )
A. a 0 b B. a b 0
C. b a 0 D. b 0 a
2.(2021 1新高考Ⅱ)已知 a log5 2, b log8 3, c ,则下列判断正确的是( )2
A. c b a B.b a c C. a c b D. a b c
3.(2021天津)若 2a 5b 10 1 1,则 ( )
a b
A. 1 B. lg7 C.1 D. log710
4.(2021天津)设 a log2 0.3, b log 1 0.4, c 0.4
0.3,则三者大小关系为( )
2
A. a b c B. c a b C.b c a D. a c b
- 9 -
5.(2020天津)设 a 30.7 b (1, ) 0.8, c log0.7 0.8,则 a, b, c的大小关系为( )3
A. a b c B.b a c C.b c a D. c a b
6.(2020新课标Ⅲ)已知 55 84,134 85 .设 a log 5 3 , b log8 5, c log13 8,则( )
A. a b c B. b a c C. b c a D. c a b
十三、函数值域
1.(2022上海)设函数 f (x)满足 f (x) f ( 1 ),定义域为 D [0, ),值域为 A,若集
x 1
合{y | y f (x), x [0, a]}可取得 A中所有值,则参数 a的取值范围为________.
2.(2021上海)已知 x1,x2 R,若对任意的 x2 x1 S , f (x2 ) f (x1) S,则有定义: f (x)
是在 S关联的.
(1)判断和证明 f (x) 2x 1是否在 [0, )关联?是否有 [0,1]关联?
(2)若 f (x)是在{3}关联的, f (x)在 x [0,3)时, f (x) x2 2x,求解不等式:2 f (x) 3.
(3)证明: f (x)是{1}关联的,且是在 [0, )关联的,当且仅当“ f (x)在 [1,2]是关联的”.
十四、函数的实际应用
1. (2022北京)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制
冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与 T和
lgP的关系,其中 T表示温度,单位是 K;P表示压强,单位是 bar.下列结论中正确的是
( )
- 10 -
A. 当T 220, P 1026时,二氧化碳处于液态
B. 当T 270, P 128时,二氧化碳处于气态
C. 当T 300, P 9987时,二氧化碳处于超临界状态
D. 当T 360, P 729时,二氧化碳处于超临界状态
2.(2021甲卷)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五
分记录法和小数记录法记录视力数据,五分记录法的数据 L和小数记录法的数据V 满足
L 5 lgV .已知某同学视力的五分记录法的数据为 4.9,则其视力的小数记录法的数据约
为( ) (1010 1.259)
A.1.5 B.1.2 C.0.8 D.0.6
十五、函数求值
1
1. (2022北京)己知函数 f (x) x ,则对任意实数 x,有( )1 2
A. f (- x)+ f (x) = 0 B. f ( x) f (x) 0
C. f ( x) f (x) 1 D. f ( x) f (x) 1
3
2. (2022全国乙卷理)已知函数 f (x), g(x)的定义域均为 R,且
f (x) g(2 x) 5, g(x) f (x 4) 7.若 y g(x)的图像关于直线 x 2对称,
22
g(2) 4,则 f (k ) ( )
k 1
A. 21 B. 22 C. 23 D. 24
- 11 -
2020-2022 函数高考题分类合集解析
一.反函数(上海)
1.【解答】函数 f (x) x3的反函数为 f 1(x),
整理得 f 1(x) 3 x;
所以 f 1(27) 3.
故答案为:3.
2.【解答】选项 A:因为函数是二次函数,属于二对一的映射,
根据函数的定义可得函数不存在反函数, A错误,
选项 B :因为函数是三角函数,有周期性和对称性,属于多对一的映射,
根据函数的定义可得函数不存在反函数, B 错误,
选项C :因为函数的单调递增的指数函数,属于一一映射,所以函数存在反函数,C 正确,
选项 D:因为函数是常数函数,属于多对一的映射,所以函数不存在反函数,D错误,
故选:C .
3 f (x) 3.【解答】因为 2,
x
令 f (x) 1 3,即 2 1,解得 x 3,
x
f 1故 (1) 3 .
故答案为: 3.
4 3.【解答】由 y f (x) x ,得 x 3 y ,
把 x 3 1与 y 互换,可得 f (x) x 的反函数为 f (x) 3 x.
故答案为: 3 x .
二.具体函数定义域
- 12 -
1
1.【解答】 y x 2 1 ,定义域为{x | x 0},
x
y x 1 1 ,定义域为{x | x 0},
x
1
y x 3 3 x ,定义域为 R,
1
y x 2 x ,定义域为{x | x 0}.
1
定义域为 R 的是 y x 3 .
故选:C.
1 1 x 0
2.【解答】因为 f x 1 x,所以 ,解得 x 1且 x 0,x x 0
故函数的定义域为 ,0 0,1 ;
故答案为: ,0 0,1
x 1 0
3.【解答】要使函数有意义,则 ,
x 0
x 1
所以 ,所以 x 0 ,
x 0
所以函数的定义域为{x | x 0},
故答案为:{x | x 0}.
三.函数的零点与方程根的关系
1.【解答】 f (x)在区间 (0, )内恰有 6个零点
又 二次函数最多有两个零点,
当 x a时, f (x) 0至少有四个根,
f (x) cos(2 x 2 a) cos[2 (x a)],
令 f (x) 0,即 2 (x a) k k Z ,
2
- 13 -
x k 1 a,
2 4
又 x (0, ),
0 k 1 a a 2a 1 1 ,即 k ,
2 4 2 2
①当 x a时, 5 2a 1 7 9 4, f (x)有 4个零点,即 a ,
2 4 4
6 2a 1 5, f (x) 5 9 a 11有 个零点,即 ,
2 4 4
7 2a 1 6 f (x) 6 11 a 13 , 有 个零点,即 ,
2 4 4
②当 x a时, f (x) x2 2(a 1)x a2 5,
△ b2 4ac 4(a 1)2 4(a2 5) 8a 16 0,解得 a 2,
当 a 2时,△ 0, f (x)无零点,
当 a 2时,△ 0, f (x)有 1个零点,
当 a 2时, f (a) a2 2a(a 1) a2 5 2a 5,
f (x)的对称轴 x a 1,即 f (a)在对称轴的左边,
5
当 2a 5 0时,即 2 a , f (x)有两个零点,
2
5
当 2a 5 0时,即 a , f (x)有 1个零点,
2
综合①②可得,若函数 f (x)在区间 (0, )内恰有 6个零点,则需满足:
7 a 9 9 a 11 11 13 4 4 4 4 a
或 或 4 4 ,
2 5 a a 5 或a 2 a 2 2 2
a (2 9解得 , ] (5 11, ].
4 2 4
故选: A.
2.【解答】函数 f (x) | lg x | kx 2的零点的个数可转化为函数 y | lg x |与直线 y kx 2的
交点的个数;
作函数 y | lg x |与直线 y kx 2的图象如右图,
若 k 0 ,则函数 y | lg x |与直线 y kx 2的图象在 (0,1)与 (1, )上各有一个交点,如直线
l1,则 f (x)有两个零点,故(1)正确;
- 14 -
当 k 2 时,当 x (0,1]时, f (x) lg x 2x 2,
f (10 2 ) 2 1 1 2 0, f (10 1) 1 2 0,
50 5
故 f (x)在 (10 2 10 1, )上至少有一个零点,
又 f (1) 0 ,结合图象知, f (x)在 (0,1]上有两个零点,
即 y | lg x |与 y 2x 2有两个不同的交点,故当直线绕点 (0, 2)顺时针旋转时,
存在直线 y kx 2与函数 y | lg x |与直线的图象相切,即 f (x)有一个零点,如直线 l2 ,故(2)
正确;
当 k 0 时,函数 y | lg x |与直线 y kx 2的图象至多有两个交点,故(3)不正确;
当 k 0 且 k足够小时,函数 y | lg x |与直线 y kx 2的图象在 (0,1)与 (1, )上分别有 1个、
2个交点,如直线 l3,故(4)正确;
故答案为:(1)(2)(4).
3.【解答】若函数 g(x) f (x) | kx2 2x | (k R)恰有 4个零点,
则 f (x) | kx2 2x |有四个根,
即 y f (x)与 y h(x) | kx2 2x |有四个交点,
当 k 0时, y f (x)与 y | 2x | 2 | x |图象如下:
- 15 -
两图象只有两个交点,不符合题意,
当 k 0时, y | kx2 2x | 2与 x轴交于两点 x1 0, x2 (x2 x1)k
图象如图所示,
1 1
当 x 时,函数 y | kx2 2x |的函数值为 ,
k k
x 1 1当 时,函数 y x的函数值为 ,
k k
所以两图象有 4个交点,符合题意,
当 k 0时,
y | kx2 2x | 2与 x轴交于两点 x1 0, x2 (x x )k 2 1
在 [0 2, )内两函数图象有两个交点,所以若有四个交点,
k
只需 y x3与 y kx2 2x (2在 , )还有两个交点,即可,
k
即 x3 kx2 2 2x在 ( , )还有两个根,
k
- 16 -
k x 2 (2即 在 , )还有两个根,
x k
函数 y x 2 2 2 ,(当且仅当 x 2 ,即 x 2 时,取等号),
x x
2
所以 0 2,且 k 2 2 ,
k
所以 k 2 2 ,
综上所述, k的取值范围为 ( , 0) (2 2 , ).
故选: D.
4.【解答】根据条件(1)可得 f (0) 0或 f (1) 1,
又因为关于 x的方程 f (x) a无实数解,所以 a 0或 1,
故 a ( , 0) (0,1) (1, ),
故答案为: ( , 0) (0,1) (1, ).
四.分段函数
1 , x 0
1.【解答】若 a 0时, f (x) ,∴ f (x) 0;
(x 2)
2 , x 0 min
若 a 0时,当 x a时, f (x) ax 1单调递增,当 x 时, f (x) ,故 f (x)没
- 17 -
有最小值,不符合题目要求;
若 a 0时,
当 x a时, f (x) ax 1单调递减, f (x) f (a) a2 1,
0 (0 a 2)
当 x a时, f (x)min {(a 2)2 (a 2)
∴ a2 1 0或 a2 1 (a 2)2,
解得0 a 1,
综上可得0 a 1;
故答案为:0(答案不唯一),1
2 7
2. 1 1 7【解答】由已知 f ( ) 2 , f ( )
7 4 37
1 ,
2 2 4 4 4 7 28
1 37
所以 f f ( ) , 2 28
当 x 1时,由1 f (x) 3可得1 x2 2 3,所以 1 x 1,
1
当 x 1时,由1 f (x) 3可得1 x 1 3,所以1 x 2 3,x
1 f (x) 3等价于 1 x 2 3,所以[a,b] [ 1,2 3],
所以b a的最大值为3 3 .
37
故答案为: ,
28 3 3
.
2
3 x 4, x 2.【解答】因为函数 f (x) ,
| x 3 | a, x 2
所以 f ( 6) ( 6)2 4 2,
则 f ( f ( 6)) f (2) | 2 3 | a 3,解得 a 2.
故答案为:2.
4.【解答】(1)按实际情况而言,交通流量 v随着道路密度 x的增大而减小,
- 18 -
故 v f (x)是单调递减函数,
所以 k 0,
当 40 x 80时, v最大为 85,
80
于是只需令100 135 (1) x 95 x 80,解得 ,
3 3
80
故道路密度 x的取值范围为 (0, ).
3
(2)把 x 80, v 50代入 v f (x) k (x 40) 85中,
7
得 50 k 40 85,解得 k .
8
80
100x 135 (
1
) x x,0 x 40
q vx 3 ,
7
(x 40)x 85x, 40 x 80 8
80
①当 0 x 40时, v 100 135 (1 ) x 100,
3
q vx 100 40 4000.
②当 40 x 80 7时, q是关于 x的二次函数, q x2 120x,
8
x 480 q 7 (480)2 120 480 28800对称轴为 ,此时 有最大值,为 4000.
7 8 7 7 7
综上所述,车辆密度 q 28800的最大值为 .
7
五.函数的图象与图象的变换
1. x
3 x
【解答】设 f x ,则 f 1 0,故排除 B;
x2 1
h x 2x cos x π设 2 ,当 x x 1
0, 时,0 cos x 1,
2
所以 h x 2x cos x 2x 2 2 1,故排除 C;x 1 x 1
g x 2sin x 2sin 3设
x2
,则 g 3 0,故排除 D.
1 10
故选:A.
2. x x【解答】令 f x 3 3 cos x, x ,
,
2 2
- 19 -
则 f x 3 x 3x cos x 3x 3 x cos x f x ,
所以 f x 为奇函数,排除 BD;
x 0, 又当 x 时,3 3 x 0,cos x 0,所以 f x 0,排除 C.
2
故选:A.
3 f (x) ln | x |.【解答】根据题意, 2 ,其定义域为{x | x 0},x 2
有 f ( x) ln | x | 2 f (x),是偶函数,排除 AC,x 2
在区间 (0,1)上, ln | x | ln x 0,必有 f (x) 0,排除D,
故选: B.
4.【解答】 y f (x) x cos x sin x,
则 f ( x) xcos x sin x f (x),
f (x)为奇函数,函数图象关于原点对称,故排除C ,D,
当 x 时, y f ( ) cos sin 0 ,故排除 B,
故选: A.
5 4x.【解答】函数 y 2 的定义域为实数集 R,关于原点对称,x 1
4x 4x
函数 y f (x) 2 ,则 f ( x) 2 f (x),则函数 y f (x)为奇函数,故排除C ,x 1 x 1
D,
当 x 0时, y f (x) 0,故排除 B,
故选: A.
6.【解答】设甲企业的污水排放量W 与时间 t的关系为W f (t),乙企业的污水排放量W 与
时间 t的关系为W g(t).
f (t ) f (t )
对于①,在 [t1, t2 ]这段时间内,甲企业的污水治理能力为
2 1 ,
t2 t1
g(t ) g(t )
乙企业的污水治理能力为 2 1 .
t2 t1
- 20 -
f (t2 ) f (t1) g(t2 ) g(t )由图可知, f (t1 ) f (t
1
2 ) g (t1 ) g (t2 ), ,t2 t1 t2 t1
即甲企业的污水治理能力比乙企业强,故①正确;
对于②,由图可知, f (t)在 t2 时刻的切线的斜率小于 g (t)在 t2 时刻的切线的斜率,但两切
线斜率均为负值,
在 t2 时刻,甲企业的污水治理能力比乙企业强,故②正确;
对于③,在 t3时刻,甲,乙两企业的污水排放都小于污水达标排放量,
在 t3时刻,甲,乙两企业的污水排放都已达标,故③正确;
对于④,由图可知,甲企业在 [0, t1],[t1, t2 ],[t2, t3 ]这三段时间中,在 [t1, t2 ]的污水
治理能力最强,
故④错误.
正确结论的序号是①②③.
故答案为:①②③.
六.函数单调性的性质与判断
1.【解答】(1) f (x) 2x , t 1, g(x)为 f (x)做 变换后的结果, g(x) 2,
g(x) f (x) f (x 1) 2x 2x 1 2x 1 2,
解得 x 2.
(2) f (x) x2 , h(x)为 f (x)做 变换后的结果, f (x) h(x) ,
x2 | (x t)2 x2 | | 2tx t 2 |,
t
当 x 时, f (x) h(x)恒成立;
2
t
当 x 时, 2tx t 2 x2 ,
2
解得 x (1 2)t,或 x (1 2)t,
综上,不等式: f (x) h(x)的解集为 ( , (1 2)t] [(1 2)t, ).
(3)证明: f (x)先做 变换后得到 u(x),u(x)再做 变换后得到 h1(x),
u(x) f (x) f (x t) , h1(x) | f (x t) f (x) [ f (x) f (x t)] |,
- 21 -
f (x)先做 变换后得到 v(x), v(x)再做 变换后得到 h2 (x),
v(x) | f (x t) f (x) |, h2 (x) | f (x t) f (x) | | f (x) f (x t) |,
h1(x) h2 (x), f (x)在 ( ,0)上单调递增,
| f (x t) f (x) [ f (x) f (x t)] | | f (x t) f (x) | | f (x) f (x t) | ,
f (x t) f (t) f (t) f (t 1)
t 0 , f (x t) f (x) 0 ,
f (x) f (x t)
函数 f (x)在 R 上单调递增.
2.【解答】由一次函数性质可知 f (x) x在 R 上是减函数,不符合题意;
2
由指数函数性质可知 f (x) ( )x在 R 上是减函数,不符合题意;
3
由二次函数的性质可知 f (x) x2在 R 上不单调,不符合题意;
根据幂函数性质可知 f (x) 3 x 在 R 上单调递增,符合题意.
故选: D.
3.【解答】(1)当 a 1时, f (x) | x 1| 1 x ,
由 | x 1| 1 0,得 | x 1| 1,解得 x 2或 x 0.
函数的定义域为 ( , 2] [0, );
(2) f (ax) | ax a | a ax ,
f (ax) a | ax a | a ax a ,
设 ax a t 0, t a t有两个不同实数根,整理得 a t t2 , t 0,
a (t 1)2 1 1 , t 0,当且仅当 0 a 时,方程有 2个不同实数根,
2 4 4
又 a 0, a的取值范围是 (0, 1);
4
(3)当 x a时, f (x) | x a | a x x x ( x 1)2 1 1 ,在 [ , )上单调递减,
2 4 4
- 22 -
a 1此时需要满足 ,即 a 1 ,函数 f (x)在[ a, )上递减;
4 4
当 x a时, f (x) | x a | a x x 2a x,在 ( , 2a]上递减,
a 1 0, 2a a 1 0,即当 a 时,函数 f (x)在 ( , a)上递减.
4 4
1
综上,当 a ( , ]时,函数 f (x)在定义域 R 上连续,且单调递减.
4
4.【解答】对于命题 q1:当 f (x)单调递减且 f (x) 0恒成立时,
当 a 0时,此时 x a x,
又因为 f (x)单调递减,
所以 f (x a) f (x)
又因为 f (x) 0恒成立时,
所以 f (x) f (x) f (a),
所以 f (x a) f (x) f (a),
所以命题 q1 命题 p,
对于命题 q2:当 f (x)单调递增,存在 x0 0使得 f (x0 ) 0,
当 a x0 0时,此时 x a x, f (a) f (x0 ) 0,
又因为 f (x)单调递增,
所以 f (x a) f (x),
所以 f (x a) f (x) f (a),
所以命题 p2 命题 p,
所以 q1, q2都是 p的充分条件,
故选:C.
5.【解答】由 2x 2y 3 x 3 y ,可得 2x 3 x 2y 3 y ,
令 f (x) 2x 3 x,则 f (x)在 R 上单调递增,且 f (x) f (y),
所以 x y ,即 y x 0,由于 y x 1 1,
故 ln(y x 1) ln1 0.
- 23 -
七.复合函数的单调性
1.【解答】由 x2 4x 5 0,得 x 1或 x 5 .
令 t x2 4x 5,
外层函数 y lg t是其定义域内的增函数,
要使函数 f (x) lg(x2 4x 5)在 (a, )上单调递增,
则需内层函数 t x2 4x 5在 (a, )上单调递增且恒大于 0,
则 (a, ) (5, ),即 a 5.
a的取值范围是 [5, ).
故选: D.
八.函数奇偶性的性质与判断
1. 【解答】因为函数 f x ln a 1 b为奇函数,所以其定义域关于原点对称.
1 x
a 1 a 1 1由 0可得, 1 x a 1 ax 0,所以 x 1,解得:a ,即函
1 x a 2
数的定义域为 , 1 1,1 1, ,再由 f 0 0可得,b ln 2.即
f x ln 1 1 ln 2 ln 1 x ,在定义域内满足 f x f x ,符合题意.
2 1 x 1 x
1
故答案为: ; ln 2.
2
a2x 1 x 0
2 .【解答】 函数 f (x) x a x 0,为奇函数, f ( x) f (x),
0 x 0
f ( 1) f (1), a2 1 (a 1),即 a(a 1) 0,求得 a 0或 a 1.
1, x 0
当 a 0时, f (x) 0, x 0 ,不是奇函数,故 a 0;
x, x 0
- 24 -
x 1, x 0
当 a 1时, f (x) 0, x 0 ,是奇函数,故满足条件,
x 1, x 0
综上, a 1,
故答案为:1.
3.【解答】因为 f x y f x y f x f y ,令 x 1, y 0可得,
2 f 1 f 1 f 0 ,所以 f 0 2,令 x 0可得, f y f y 2 f y ,即
f y f y ,所以函数 f x 为偶函数,令 y 1得,
f x 1 f x 1 f x f 1 f x ,即有 f x 2 f x f x 1 ,从而可知
f x 2 f x 1 , f x 1 f x 4 ,故 f x 2 f x 4 ,即
f x f x 6 ,所以函数 f x 的一个周期为6.
因为 f 2 f 1 f 0 1 2 1, f 3 f 2 f 1 1 1 2,
f 4 f 2 f 2 1, f 5 f 1 f 1 1, f 6 f 0 2,所以
一个周期内的 f 1 f 2 f 6 0.由于 22除以 6余 4,
22
所以 f k f 1 f 2 f 3 f 4 1 1 2 1 3.
k 1
故选:A.
4.【解答】 f (x 1)为奇函数, f (1) 0,且 f (x 1) f ( x 1),
f (x 2)偶函数, f (x 2) f ( x 2),
f [(x 1) 1] f [ (x 1) 1] f ( x) ,即 f (x 2) f ( x),
f ( x 2) f (x 2) f ( x).
令 t x,则 f (t 2) f (t) ,
f (t 4) f (t 2) f (t), f (x 4) f (x).
当 x [1, 2]时, f (x) ax2 b.
f (0) f ( 1 1) f (2) 4a b,
- 25 -
f (3) f (1 2) f ( 1 2) f (1) a b,
又 f (0) f (3) 6, 3a 6,解得 a 2,
f (1) a b 0, b a 2,
当 x [1, 2]时, f (x) 2x2 2,
f (9) 1 3 9 5 f ( ) f ( ) ( 2 2) .
2 2 2 4 2
故选: D.
5.【解答】因为 f (x) 1 x (x 1) 2 2 1 ,
1 x 1 x x 1
所以函数 f (x)的对称中心为 ( 1, 1),
所以将函数 f (x)向右平移一个单位,向上平移一个单位,
得到函数 y f (x 1) 1,该函数的对称中心为 (0,0),
故函数 y f (x 1) 1为奇函数.
故选: B.
6.【解答】由题意得 f ( x) f (x),
又 f (1 x) f ( x) f (x) ,
所以 f (2 x) f (x),
又 f ( 1 1 ) ,
3 3
则 f (5) f (2 1 ) f ( 1 ) 1 .
3 3 3 3
故选:C.
7.【解答】函数 f (x) x3(a 2x 2 x )是偶函数,
y x3为 R 上的奇函数,
故 y a 2x 2 x也为 R 上的奇函数,
所以 y | a 20x 0 2
0 a 1 0,
所以 a 1.
8.【解答】 函数 f (x 2)为偶函数,
- 26 -
f (2 x) f (2 x),
f (2x 1)为奇函数,
f (1 2x) f (2x 1),
用 x替换上式中 2x 1,得 f (2 x) f (x),
f (2 x) f (x), f (4 x) f (2 x) f (x) ,即 f (x) f (x 4),
故函数 f (x)是以 4为周期的周期函数,
f (2x 1)为奇函数,
f (1 2x) f (2x 1),即 f (2x 1) f ( 2x 1) 0 ,
用 x替换上式中 2x 1,可得, f (x) f (2 x) 0,
f (x)关于 (1,0)对称,
又 f (1) 0,
f ( 1) f (2 1) f ( 1) 0 .
故选: B.
9.【解答】 y f (x)是奇函数,可得 f ( x) f (x),
2 2
当 x 0时, f (x) x 3 ,可得 f (8) 83 4,
则 f ( 8) f (8) 4,
故答案为: 4.
10.【解答】 y 3x在 R 上单调递减且为奇函数, A符合题意;
因为 y x3在 R 上是增函数, B不符合题意;
y log3 x, y 3
x 为非奇非偶函数,C 不符合题意;
故选: A.
11.【解答】 函数 y f (x)为定义域为 R 的奇函数,其图像关于 x 1对称,且当 x (0,1]
时, f (x) lnx,
f (x)是周期为 4的周期函数,图象如图:
- 27 -
将方程 f (x) x 1的正实数根从小到大依次记为 x1, x2, x3 , , xn,
则 lim(xn 1 xn )的几何意义是两条渐近线之间的距离 2,n
lim(x x ) 2.
n n 1 n
故答案为:2.
九.奇偶性与单调性的综合
1.【解答】因为 f (x) cos x cos2x cos x (2cos2 x 1) 2cos2 x cos x 1,
因为 f ( x) 2cos2 ( x) cos( x) 1 2cos2 x cos x 1 f (x),
故函数 f (x)为偶函数,
令 t cos x,则 t [ 1,1],
故 f (t) 2t2 t 1是开口向下的二次函数,
t 1 1 f (t) 1 1 1 9所以当 时, 取得最大值 f ( ) 2 ( )2 1 ,
2 ( 2) 4 4 4 4 8
9
故函数的最大值为 .
8
综上所述,函数 f (x) 9是偶函数,有最大值 .
8
故选: D.
2.【解答】若函数 f (x)在 [0,1]上单调递增,
则函数 f (x)在 [0,1]上的最大值为 f (1),
若 f (x) (x 1 )2 ,则函数 f (x)在[0,1]上的最大值为 f (1),
3
但函数 f (x)在 [0,1]上不单调,
- 28 -
故选: A.
3.【解答】根据题意,依次判断选项:
对于 A, f (x) cos x 1, f (x)为偶函数,且关于点 (1,1)对称,存在最大值, A错误,
2
对于 B, f (x) cos( x) , f (x)为偶函数且关于直线 x 1对称,存在最大值, B错误,
对于C,假设 f (x)有最大值,设其最大值为M ,其最高点的坐标为 (a,M ),
f (x)为奇函数,其图象关于原点对称,则 f (x)的图象存在最低点 ( a, M ),
又由 f (x)的图象关于点 (1,1)对称,则 ( a, M )关于点 (1,1)对称的点为 (2 a, 2 M ),
与最大值为M 相矛盾,则此时 f (x)无最大值,C 正确,
对于 D, f (x) sin x , f (x)为奇函数且关于直线 x 1对称, D错误,
2
故选:C.
4.【解答】 定义在 R 的奇函数 f (x)在 ( , 0)单调递减,且 f (2) 0 , f (x)的大致图象如
图:
f (x)在 (0, )上单调递减,且 f ( 2) 0;
故 f ( 1) 0;
当 x 0 时,不等式 xf (x 1) 0成立,
当 x 1时,不等式 xf (x 1) 0成立,
当 x 1 2或 x 1 2 时,即 x 3或 x 1时,不等式 xf (x 1) 0成立,
当 x 0 时,不等式 xf (x 1) 0等价为 f (x 1) 0,
x 0
此时 ,此时1 x 3,
0 x 1 2
当 x 0 时,不等式 xf (x 1) 0等价为 f (x 1) 0,
- 29 -
x 0
即 ,得 1 x 0,
2 x 1 0
综上 1 x 0或1 x 3,
即实数 x的取值范围是 [ 1, 0] [1,3],
故选: D.
2x 1 0
5 1.【解答】由 ,得 x .
2x 1 0 2
又 f ( x) ln | 2x 1| ln | 2x 1| (ln | 2x 1| ln | 2x 1|) f (x),
f (x)为奇函数;
f (x) ln | 2x 1| ln | 2x 1| ln | 2x 1| ln | 2x 1由 |,
| 2x 1| 2x 1
2x 1 2x 1 2 1 2 2 1 1 1 .
2x 1 2x 1 2x 1 2(x 1) x 1
2 2
t | 2x 1可得内层函数 |的图象如图,
2x 1
1 1 1
在 ( , )上单调递减,在 ( , )上单调递增,
2 2 2
1
则 ( , ) 上单调递减.
2
又对数式 y ln t是定义域内的增函数,
f (x) ( , 1由复合函数的单调性可得, 在 )上单调递减.
2
故选: D.
- 30 -
十.指对数函数的图象与性质
1.【解答】(1)因为函数 f (x) log3 (a x) log3 (6 x),
将函数 f (x)图像向下移m(m 0)后,得 y f (x) m log3 (a x) log3 (6 x) m的图像,
由函数图像经过点 (3,0)和 (5,0),
log3(3 a) 1 m 0
所以 ,
log3(5 a) 0 m 0
解得 a 2,m 1.
(2) a 3且 a 0时,不等式 f (x) f (6 x)可化为
log3 (a x) log3 (6 x) log3 (a 6 x) log3 x,
a x 0
6 x 0
等价于 a 6 x 0 ,
x 0
(a x)(6 x) x(a 6 x)
x a
x 6
解得 x a 6 ,
x 0
a(x 3) 0
当 3 a 0时, 0 a 3, 3 a 6 6,解不等式得 a x 3,
当 a 0时, a 0, a 6 6,解不等式得 3 x 6;
综上知, 3 a 0时,不等式 f (x) f (6 x)的解集是 ( a, 3],
a 0时,不等式 f (x) f (6 x)的解集是 [3, 6).
2.【解答】因为2a 5,b log 3
1
log 3,即 23b8 2 3,所以3
a
a 3b 4 2a
2
524 25
43b
3b 2 32
.
2 9
- 31 -
故选:C.
3 a b.【解答】因为 2 log2 a 4 2log4 b 2
2b log2 b;
22b log b 22b 2b因为 2 log2 2b 2 log2 b 1,
2a log a 22b所以 2 log2 2b,
令 f (x) 2x log2 x,由指对数函数的单调性可得 f (x)在 (0, )内单调递增;
且 f (a) f (2b) a 2b;
故选: B .
十一、指数函数的实际应用
K
1 * 1.【解答】由已知可得 * 0.95K,解得 0.23(t 53) ,
1 e 0.23(t 53)
e
19
0.23(t*两边取对数有 53) ln19,
解得 t* 66,
故选:C .
十二、指对大小的比较
lg10
1.【解答】由9m 10可得m log910 1,而lg9
2 2 lg10 lg11
lg9lg11 lg9 lg11 lg99 1 lg10
2
,所以 ,即m lg11,所
2 2 lg9 lg10
以 a 10m 11 10lg11 11 0.
lg8 lg10 2 lg80 2 2 lg9 lg10
又 lg8lg10 lg9 ,所以 ,即 log2 2 lg8 lg9 8
9 m,
所以b 8m 9 8log8 9 9 0.综上, a 0 b.
- 32 -
故选:A.
1 1 12 log 2 log 5 2 log 3 log 8 2 1.【解答】 5 5 , 8 8 ,2 2
a c b.
故选:C.
3.【解答】 2a 5b 10, a log210,b log510,
1 1 1 1
log10 2 log10 5 lg10 1,a b log210 log510
故选:C.
4.【解答】 log2 0.3 log21 0, a 0,
log1 0.4 log1 0.5 1, b 1,
2 2
0 0.40.3 0.40 1, 0 c 1,
a c b,
故选: D.
5.【解答】 a 30.7 , b (1 ) 0.8 30.8,
3
则 b a 1,
log0.7 0.8 log0.7 0.7 1,
c a b,
故选: D.
6 3 3.【解答】由 log5 5 log 8,4 4 8
3 3
log5 54 log 3,而 log 845 8 log8 5
log5 3 log8 5,
即 a b ;
55 84 , 5 4 log5 8, log 5 8 1.25, b log8 5 0.8;
134 85 , 4 5 log13 8, c log13 8 0.8, c b ,
- 33 -
综上, c b a.
故选: A.
十三、函数值域
1 1.【解答】令 x 得,
x 1
x 5 1 5 1 或 x (舍去);
2 2
当 x 5 1 时,
2
1 1 5 1
,
x 1 5 1 2
1
2
x 5 1故对任意 ,
2
x [0 5 1都存在 0 , ]
1
, x ,
2 x 1 0
故 f (x) f (x0 ),
0 x 5 1而当 时,
2
1 1 5 1
,
x 1 5 1 2
1
2
故 A {y | y f (x) x [0 5 1, , ]},
2
故当 A {y | y f (x), x [0, a]}时,
[0 5 1, ] [0, a],
2
a 5 1故参数 的最小值为 ,
2
a [ 5 1故参数 的取值范围为 , ),
2
5 1
故答案为: [ , ).
2
2.【解答】(1) f (x)在 [0, )关联,在 [0,1]不关联,
任取 x1 x2 [0, ),则 f (x1) f (x2 ) 2(x1 x2 ) [0, ), f (x)在 [0, )关联;
- 34 -
取 x1 1, x2 0,则 x1 x2 1 [0,1],
f (x1) f (x2 ) 2(x1 x2 ) 2 [0,1], f (x)在 [0,1]不关联;
(2) f (x)在{3}关联, 对于任意 x1 x2 3,都有 f (x1) f (x2 ) 3,
对任意 x,都有 f (x 3) f (x) 3,
由 x [0, 3)时, f (x) x2 2x,得 f (x)在 x [0, 3)的值域为 [ 1, 3),
f (x)在 x [3, 6)的值域为 [2, 6),
2 f (x) 3仅在 x [0, 3)或 x [3, 6)上有解,
x [0, 3)时, f (x) x2 2x,令 2 x2 2x 3,解得 3 1 x 3,
x [3, 6)时, f (x) f (x 3) 3 x2 8x 18,令 2 x2 8x 18 3,解得 3 x 5,
不等式 2 f (x) 3的解为 [ 3 1, 5],
(3)证明:①先证明: f (x)是在{1}关联的,且是在 [0, )关联的 f (x)在 [1, 2]是关联
的,
由已知条件可得, f (x 1) f (x) 1,
f (x n) f (x) n, n Z ,
又 f (x)是在 [0, )关联的,
任意 x2 x1, f (x2 ) f (x1)成立,
若1 x2 x1 2,
x1 1 x2 x1 2,
f (x1 1) f (x2 ) f (x1 2),即 f (x1) 1 f (x2 ) f (x1) 2,
1 f (x2 ) f (x1) 2,
f (x)是[1, 2]关联,
②再证明: f (x)在 [1, 2]是关联的 f (x)是在{1}关联的,且是在[0, )关联的,
f (x)在[1, 2]是关联的, 任取 x1 x2 [1, 2],都有 f (x1) f (x2 ) [1, 2]成立,
即满足1 x1 x2 2,都有1 f (x1) f (x2 ) 2,
下面用反证法证明 f (x 1) f (x) 1,
- 35 -
若 f (x 1) f (x) 1,则 f (x 2) f (x) f (x 2) f (x 1) f (x 1) f (x) 2 ,与 f (x)在 [1,
2]是关联的矛盾,
若 f (x 1) f (x) 1,而 f (x)在 [1, 2]是关联的,则 f (x 1) f (x) 1,矛盾,
f (x 1) f (x) 1成立,即 f (x)是在{1}关联的,
再证明 f (x)是在 [0, )关联的,
任取 x1 x2 [n, )(n N ),则存在 n N ,使得任取 x1 x2 [n, n 1](n N ),
1 x1 (n 1) x2 2,
f [x1 (n 1)] f (x2 ) f (x1) (n 1) f (x2 ) [1, 2],
f (x1) f (x2 ) [n, n 1] [0, ),
f (x)是在 [0, )关联的;
综上所述, f (x)是{1}关联的,且是在[0, )关联的,当且仅当“ f (x)在 [1,2]是关联的”,
故得证.
十四、函数的实际应用
1.【解答】当T 220,P 1026时, lg P 3,此时二氧化碳处于固态,故 A错误.
当T 270, P 128时, 2 lg P 3,此时二氧化碳处于液态,故 B错误.
当T 300, P 9987时, lgP与 4非常接近,故此时二氧化碳处于固态,
另一方面,T 300时对应的是非超临界状态,故 C错误.
当T 360, P 729时,因 2 lg P 3 , 故此时二氧化碳处于超临界状态,故 D正确.
故选:D
2.【解答】在 L 5 lgV 中, L 4.9,所以 4.9 5 lgV ,即 lgV 0.1,
解得V 10 0.1 1 1 1
100.1
0.8 ,
1010 1.259
所以其视力的小数记录法的数据约为 0.8.
故选:C.
- 36 -
十五、函数求值
x
1. 【解答】 f x f x 1 1 2 1 1,故 A错误,C正确;
1 2 x 1 2x 1 2x 1 2x
x x
f x f x 1 1 2 1 2 1 2 1 ,不是常数,故 BD
1 2 x 1 2x 1 2x 1 2x 2x 1 2x 1
错误;
故选:C.
2.【解答】因为 y g(x)的图像关于直线 x 2对称,
所以 g 2 x g x 2 ,
因为 g(x) f (x 4) 7,所以 g(x 2) f (x 2) 7,即 g(x 2) 7 f (x 2),
因为 f (x) g(2 x) 5,所以 f (x) g(x 2) 5,
代入得 f (x) 7 f (x 2) 5,即 f (x) f (x 2) 2,
所以 f 3 f 5 f 21 2 5 10,
f 4 f 6 f 22 2 5 10 .
因为 f (x) g(2 x) 5,所以 f (0) g(2) 5,即 f 0 1,所以
f (2) 2 f 0 3 .
因为 g(x) f (x 4) 7,所以 g(x 4) f (x) 7,又因为 f (x) g(2 x) 5,
联立得, g 2 x g x 4 12,
所以 y g(x)的图像关于点 3,6 中心对称,因为函数 g(x)的定义域为 R,
所以 g 3 6
因为 f (x) g(x 2) 5,所以 f 1 5 g 3 1 .
所以
- 37 -
22
f (k) f 1 f 2 f 3 f 5 f 21 f 4 f 6 f 22 1 3 10 10 24
k 1
故选:D
- 38 -
同课章节目录
