5.2.1 平行线 课件(共20张PPT)
文档属性
| 名称 | 5.2.1 平行线 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 16:54:26 | ||
图片预览







文档简介
(共20张PPT)
5.2.1 平行线
华师大版 七年级上册
教学目标
【教学目标】
1.让学生理解在同一平面内的两条直线的位置关系只有相交和平行;
2.让学生理解平行公理,并会用直尺过直线外一点作已知直线的平行线;
3.培养学生积极动手的能力,并使其获取成功的喜悦感,感受数学与生活的密切联系.
【重点】平行线的定义、公理和推论.
【难点】平行公理及推论的应用.
复习回顾
在同一平面内,两条直线有怎样的位置关系呢?
a
b
b
a
不相交
相交
如上图,在同一平面内,两条直线的位置关系有相交和不相交两种.
新知探究
在同一平面内,不相交的两条直线叫做平行线.
①“在同一平面内” ,是前提条件.
② “不相交”,就是没有交点.
③平行线指的是“两条直线” ,而不是两条射线或线段.
平行线的定义包含三层含义
新知探究
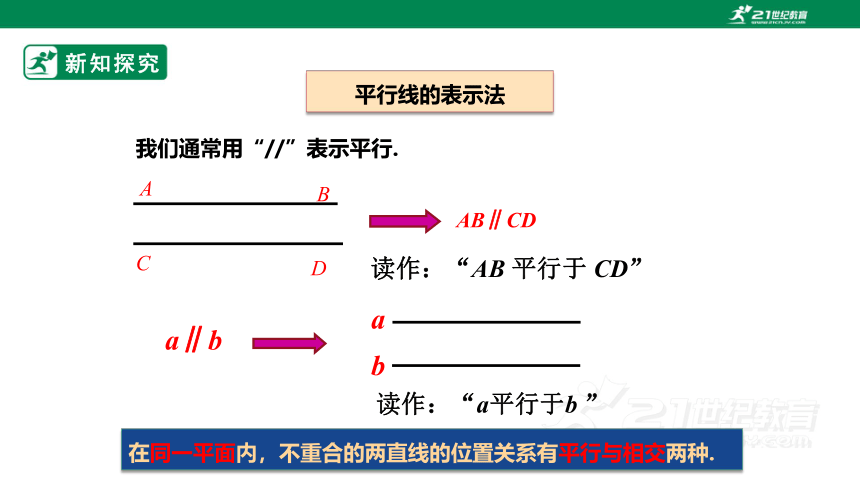
我们通常用“//”表示平行.
C
B
A
D
a∥b
AB∥CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
在同一平面内,不重合的两直线的位置关系有平行与相交两种.
平行线的表示法
新知探究
动手画一画:平行线的画法:
(1) 放
(2) 靠
(3) 推
(4) 画
平行线的画法
新知探究
如图所示,不少国家的国旗、团体或公司的标志的图案是由平行线、垂线构成的.
你能再举出一些例子吗
思考:找出图中的平行线.
新知探究
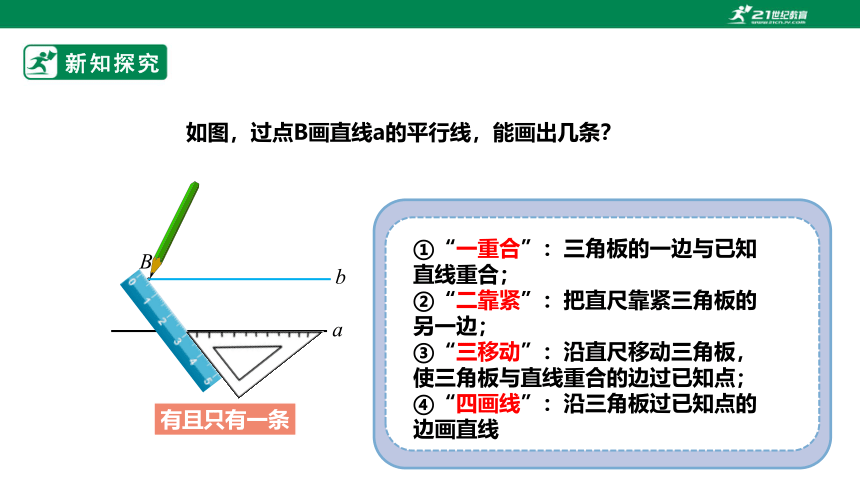
如图,过点B画直线a的平行线,能画出几条?
B
a
.
b
有且只有一条
①“一重合”:三角板的一边与已知直线重合;
②“二靠紧”:把直尺靠紧三角板的另一边;
③“三移动”:沿直尺移动三角板,使三角板与直线重合的边过已知点;
④“四画线”:沿三角板过已知点的边画直线
新知探究
B
a
.
如图,再过点C画直线a的平行线,能画出几条?
b
有且只有一条
C
.
c
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理
新知探究
画一条直线a,按图所示的方法,画一条直线b与直线a平行,再向上推三角尺,画另一条直线c,也与直线a平行.
你发现直线b与直线c有什么关系 你的同伴是否也有类似的发现
直线b与直线c也是平行的
新知探究
几何语言表达:
c
b
a
如果两条直线都与第三条直线平行,那么这两条直线互相平行.
∵a//c,c//b(已知)
∴a//b.
平行公理的推论
课堂练习
1.下列说法中,正确的有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A.1个 B.2个 C.3个 D.4个
B
课堂练习
2.下列说法中,错误的有( )
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
B
课堂练习
①过A点作AE∥BC,交 于点E ;
④过D点作DH∥BC,交 于点H ;
③过C点作CG∥AD,交AB的 于点G ;
3.如图,根据要求填空.
DC
延长线
BA的延长线
②过B点作BF∥AD,交 于点F ;
A
B
C
D
E
F
G
H
DC
课堂练习
4.如图,在同一平面内,若AB∥CD,EF与AB相交于点P,EF能与CD平行吗?为什么?
答:假设EF∥CD,
又因为AB∥CD,
根据平行于同一条直线的两条直线平行,
有AB∥EF.
这与AB和EF相交于P点矛盾,
所以EF与CD不平行.
课堂练习
5.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
A
E
B
C
D
F
答:因为CD∥EF,EF∥AB
所以CD∥AB
即如果两条直线都和第三条直线平行,
那么这两条直线也互相平行.
课堂小结
两直线位置在同一平面内
定 义
画法
性质
相交
平行
在同一平面内,不相交的两条直线.
四步法:(1) 放;(2) 靠;(3) 推;(4) 画.
平行公理(确定性)
平行公理推论(传递性)
B
a
C
b
c
a
b
a
b
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
5.2.1 平行线
华师大版 七年级上册
教学目标
【教学目标】
1.让学生理解在同一平面内的两条直线的位置关系只有相交和平行;
2.让学生理解平行公理,并会用直尺过直线外一点作已知直线的平行线;
3.培养学生积极动手的能力,并使其获取成功的喜悦感,感受数学与生活的密切联系.
【重点】平行线的定义、公理和推论.
【难点】平行公理及推论的应用.
复习回顾
在同一平面内,两条直线有怎样的位置关系呢?
a
b
b
a
不相交
相交
如上图,在同一平面内,两条直线的位置关系有相交和不相交两种.
新知探究
在同一平面内,不相交的两条直线叫做平行线.
①“在同一平面内” ,是前提条件.
② “不相交”,就是没有交点.
③平行线指的是“两条直线” ,而不是两条射线或线段.
平行线的定义包含三层含义
新知探究
我们通常用“//”表示平行.
C
B
A
D
a∥b
AB∥CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
在同一平面内,不重合的两直线的位置关系有平行与相交两种.
平行线的表示法
新知探究
动手画一画:平行线的画法:
(1) 放
(2) 靠
(3) 推
(4) 画
平行线的画法
新知探究
如图所示,不少国家的国旗、团体或公司的标志的图案是由平行线、垂线构成的.
你能再举出一些例子吗
思考:找出图中的平行线.
新知探究
如图,过点B画直线a的平行线,能画出几条?
B
a
.
b
有且只有一条
①“一重合”:三角板的一边与已知直线重合;
②“二靠紧”:把直尺靠紧三角板的另一边;
③“三移动”:沿直尺移动三角板,使三角板与直线重合的边过已知点;
④“四画线”:沿三角板过已知点的边画直线
新知探究
B
a
.
如图,再过点C画直线a的平行线,能画出几条?
b
有且只有一条
C
.
c
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理
新知探究
画一条直线a,按图所示的方法,画一条直线b与直线a平行,再向上推三角尺,画另一条直线c,也与直线a平行.
你发现直线b与直线c有什么关系 你的同伴是否也有类似的发现
直线b与直线c也是平行的
新知探究
几何语言表达:
c
b
a
如果两条直线都与第三条直线平行,那么这两条直线互相平行.
∵a//c,c//b(已知)
∴a//b.
平行公理的推论
课堂练习
1.下列说法中,正确的有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A.1个 B.2个 C.3个 D.4个
B
课堂练习
2.下列说法中,错误的有( )
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
B
课堂练习
①过A点作AE∥BC,交 于点E ;
④过D点作DH∥BC,交 于点H ;
③过C点作CG∥AD,交AB的 于点G ;
3.如图,根据要求填空.
DC
延长线
BA的延长线
②过B点作BF∥AD,交 于点F ;
A
B
C
D
E
F
G
H
DC
课堂练习
4.如图,在同一平面内,若AB∥CD,EF与AB相交于点P,EF能与CD平行吗?为什么?
答:假设EF∥CD,
又因为AB∥CD,
根据平行于同一条直线的两条直线平行,
有AB∥EF.
这与AB和EF相交于P点矛盾,
所以EF与CD不平行.
课堂练习
5.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
A
E
B
C
D
F
答:因为CD∥EF,EF∥AB
所以CD∥AB
即如果两条直线都和第三条直线平行,
那么这两条直线也互相平行.
课堂小结
两直线位置在同一平面内
定 义
画法
性质
相交
平行
在同一平面内,不相交的两条直线.
四步法:(1) 放;(2) 靠;(3) 推;(4) 画.
平行公理(确定性)
平行公理推论(传递性)
B
a
C
b
c
a
b
a
b
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
