人教B版高中数学选择性必修第一册《圆与圆的位置关系》名师课件(共49张PPT)
文档属性
| 名称 | 人教B版高中数学选择性必修第一册《圆与圆的位置关系》名师课件(共49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 20:00:04 | ||
图片预览










文档简介
(共49张PPT)
问题1:点与圆的位置关系有哪几种 如何判断
问题2:直线与圆的位置关系有哪几种 如何判断
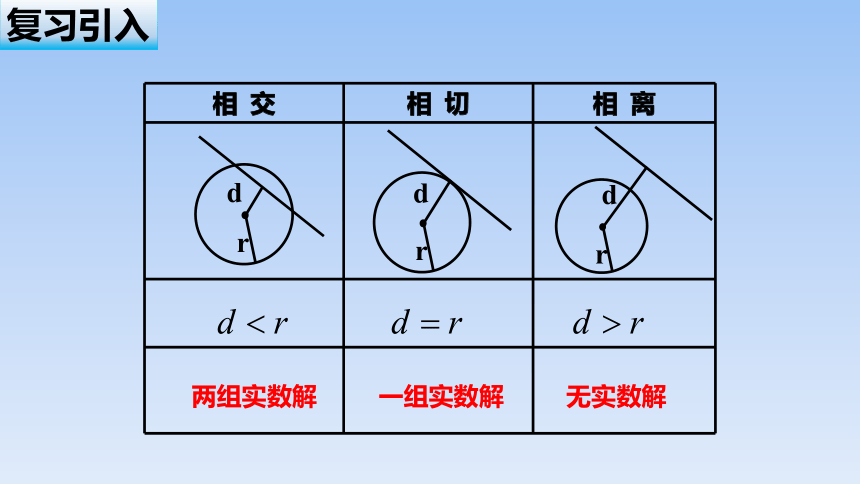
复习引入
直线
相 交 相 切 相 离
d
r
d
r
d
r
两组实数解
一组实数解
无实数解
复习引入
初中学过的平面几何中,圆与圆的位置关系有几种 我们怎样判断圆与圆的位置关系呢
复习引入
人教B版同步教材名师课件
圆与圆的位置关系
学习目标
学 习 目 标 核心素养
体会几何法 掌握利用圆心与圆心的距离与两圆半径的关系判定圆与圆的位置关系的步骤 数学抽象
数学运算
处理圆与圆相切的问题时,注意内切与外切均属于相切,在不能确定的情况下应分类讨论 数学抽象
数学运算
体会求两圆的公共弦的方法及步骤 数学运算
学习目标
学习目标:
1.理解圆与圆的位置关系的种类.
2.掌握圆与圆的位置关系的代数判断方法与几何判断方法,能够利用上述方法判断两圆的位置关系.
学科核心素养:
通过圆与圆的位置关系的推导,提升逻辑推理、直观想象、数学运算的数学素养.
探究新知
探究新知
探究新知
日环食现象
通过刚才对日全食的观察,想象一下两圆有没有出现公共点 公共点的个数是怎样的
探究新知
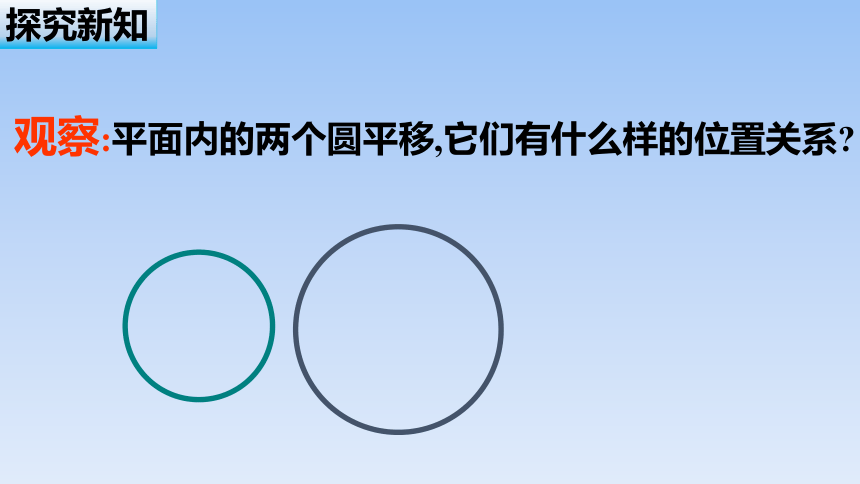
观察:平面内的两个圆平移,它们有什么样的位置关系
探究新知
两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离.
外离
思考:这两圆的
位置关系
探究新知
外切
两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫这两个圆外切.这个唯一的公共点叫做切点.
探究新知
两个圆有两个公共点,此时叫做这两个圆相交.
相交
探究新知
两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.这个唯一的公共点叫做切点.
内切
探究新知
两个圆外切和内切统称两个圆相切
探究新知
两个圆没有公共点,并且一个圆上的点在另一个圆的内部时叫做这两个圆内含.
内含
两圆同心是两圆内含的一种特例
探究新知
在图中有两圆的多种位置关系,请你找出还没有的位置关系是 .
相交
探究新知
分别观察两圆R、r和d有何数量关系
两圆外切
d=R+r
两圆内切
d=R r(R>r)
两圆外离
d>R+r
两圆内含
dr)
O2
O1
R
r
d
o1
o2
R
r
d
O1
O2
d
R
r
R
d
r
O1
O2
探究新知
思考:两圆相交时,它们的数量关系如何
两圆相交
R r(Rr)
探究新知
O1
O2
R
r
d
A
O1
O2
R
r
d
两圆的位置关系的数量特征
两圆外离
两圆外切
定义:连接两圆圆心的线段的长度叫做两圆的圆心距,一般记为d.
d=R+r
d=R r
两圆内含
R r两圆相交
两圆内切
d>R+r
d探究新知
位置关系 d 和R、 r关系 交点
两圆外离 d >R+ r 0
两圆外切 d =R+ r 1
两圆相交 R r两圆内切 R r =d 1
两圆内含 R r >d 0
性质
判定
0
R―r
R+r
同心圆
内含
外离
外切
相交
内切
位 置 关 系 数 字 化
d
探究新知
两圆位置关系的性质与判定
1、通过两圆圆心的直线叫做连心线.
2、两圆圆心之间的距离简称为圆心距.
探究新知
相切两圆的性质
圆是轴对称图形,两个圆是否也组成一个轴对称图形
我们发现通过两圆圆心的直线(连心线)是它的对称轴.
两圆相切时,由于切点是它们唯一的公共点,所以切点一定在对称轴上.
如果两圆相切,那么连心线必过切点
O1
O2
T
O1
O2
经过两圆圆心的直线叫做连心线
探究新知
两圆的对称性
思考:两圆相交时,它们的连心线与公共弦的关系
O1
O2
A
O1
O2
相交两圆的连心线垂直平分公共弦
探究新知
定理 两圆相交时,连心线垂直平分两圆的公共弦
定理 两圆相切时,连心线通过切点
探究新知
法一:圆C1与圆C2的方程联立,得到方程组,① ②,得 x+2y 1=0, ③
由③,得.把上式代入①,并整理,得④
方程④的判别式
所以,方程④有两个不相等的实数根x1,x2分别代入方程③,得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).所以圆C1与圆C2相交.
典例讲解
解析
例1 设圆C1:x2+y2+2x+8y 8=0,圆C2:x2+y2 4x 4y 2=0,试判断圆C1与圆C2的关系.
典例讲解
解析
例1 设圆C1:x2+y2+2x+8y 8=0,圆C2:x2+y2 4x 4y 2=0,试判断圆C1与圆C2的关系.
而
所以圆C1与圆C2相交.
法二: 把圆C1的方程化为标准方程,得
圆C1的圆心是点( 1, 4),半径长r1=5.
把圆C2的方程化为标准方程,得
圆C2的圆心是点(2,2),半径长r2=.
圆C1与圆C2的连心线长为
又
变式训练
1.判断圆C1: x2+y2+4x+8y 5=0与圆C2: x2+y2 4x+4y 1=0的位置关系.
由已知,得C1( 2, 4) , r1=5 , C2( 2, 2) , r2=3 ,
则d=|C1C2|=2=|r1 r2| , ∴两圆内切.
解析
2.两点到直线的距离分别是和5,满足条件的直线共有多少条
y
A
B
O
.
.
(2,2)
( 1, 4)
x
变式训练
典例讲解
(1),, ,
由题意知,,解得或.
(2)设所求圆的方程为,
由圆与直线相切、半径为4,则圆心的坐标为或.
已知圆的圆心的坐标为(2,1),半径为3.
由两圆相切,则或.
例2、(1)圆与相外切,则的值是____________________.
(2)求半径为4,与圆相切,且和直线相切的圆的方程.
或
解析
典例讲解
例2、(1)圆与相外切,则的值是____________________.
(2)求半径为4,与圆相切,且和直线相切的圆的方程.
或
解析
①当圆心为时,或
(无解),故可得,故所求圆的方程为
或.
②当圆心为时,或
(无解),解得.故所求圆的方程为或.
典例讲解
例2、(1)圆与相外切,则的值是____________________.
(2)求半径为4,与圆相切,且和直线相切的圆的方程.
或
解析
综上所述,所求圆的方程为或或.
方法归纳
处理两圆相切问题的两个步骤
(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须分两圆内切还是外切两种情况讨论.
(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值(内切时)或两圆半径之和(外切时).
变式训练
已知圆的方程可化为,则圆心为C(1,0),半径为1.
设所求圆的方程为.
由题意,可得解得或
即所求圆的方程为或
3.求与圆外切且与直线相切于点的圆的方程.
解析
典例讲解
(1)设两圆交点为,,则两点坐标
是方程组的解.① ②,得.
∵ 两点坐标都满足此方程,
∴ 即为两圆公共弦所在直线的方程.
例3、已知圆.
(1)求两圆公共弦所在直线的方程;
(2)求经过两圆交点且圆心在直线上的圆的方程.
解析
典例讲解
例3、已知圆.
(1)求两圆公共弦所在直线的方程;
(2)求经过两圆交点且圆心在直线上的圆的方程.
解析
(2)法一:解方程组得两圆的交点, .
设所求圆的圆心为因圆心在直线上,故.
则,
解得,故圆心为,半径为.
故圆的方程为,即
典例讲解
例3、已知圆.
(1)求两圆公共弦所在直线的方程;
(2)求经过两圆交点且圆心在直线上的圆的方程.
解析
法二:设所求圆的方程为
其圆心为,代入,解得.故所求圆的方程为
方法归纳
1.求两圆公共弦长的方法
一是联立两圆方程求出交点坐标,再用距离公式求解;
二是先求出两圆公共弦所在的直线方程,再利用半径长、弦心距和弦长的一半构成的直角三角形求解.
2.过两圆的交点的圆的方程
已知圆与圆相交,则过两圆交点的圆的方程可设为
变式训练
由例题解析知道是公共弦所在的直线的方程.
因圆的圆心, .
到直线的距离.
∵ 即两圆的公共弦长为
弦的中垂线也就是所在的直线.
∵ ,.
∴的中垂线方程为即.
4.在本例条件不变时,求两圆的公共弦长及公共弦的中垂线的方程.
解析
变式训练
根据条件可知,所求的圆就是以为直径的圆.
∵ 所在直线方程为
所在直线方程为.
∴由得圆心,
又∵ , ∴半径 ,
故所求圆的方程为.
5.本例条件不变,求过两圆的交点且半径最小的圆的方程.
解析
(1)设圆O1:x2+y2+D1x+E1y+F1=0,圆O2:x2+y2+D2x+E2y+F2=0.
则两圆相交公共弦所在直线方程为:
(x2+y2+D1x+E1y+F1) (x2+y2+D2x+E2y+F2)=0,
即(D1 D2)x+(E1 E2)y+(F1 F2)=0.
两圆相交时公共弦问题
素养提炼
两圆相交时公共弦问题
素养提炼
(2)求两圆的公共弦长问题可转化为直线与圆相交求相交弦长问题,从而得以解决,如图,利用圆O1,首先求出O1点到相交弦所在直线的距离d,而所以即,从而得以解决.
当堂练习
将圆的一般方程化为标准方程,
,∴ , , , .
从而 ,∴ .
因此两圆的位置关系为相交.故选C.
1. 圆与的位置关系是( )
A.外离 B.外切 C.相交 D.内含
C
解析
的垂直平分线过两圆的圆心,把圆心代入,即可排除A,B,D.故选C.
2.圆和圆交于两点,则的垂直平分线的方程是( )
A.B. C.D.
解析
C
当堂练习
, ,两圆半径均为1,∵,∴ 的最小值为.
3.已知点在圆上运动,点在圆上运动,则的最小值为_____.
解析
设所求圆的方程为把原点代入可得,所以,即可得过圆与圆的两个交点且过原点O的圆的方程为:.
4.已知圆,,则过圆与圆的两个交点且过原点O的圆的方程为________________.
解析
当堂练习
设圆的半径为,圆心距为,
当圆与圆外切时, , ,
当圆与圆内切时, , ,
圆的方程为或.
5.已知以为圆心的圆与圆: 相切,求圆的方程.
解析
说说这节课你的收获吧!
位置关系 图形 交点个数
外离
内含
外切
相离
相交
内切
相切
0
2
1
d>R+r
0 ≤ d<R r
R r <d<R+r
d=R+r
d=R r
圆与圆的位置关系 数量关系
思想方法:类比方法与分类讨论
性质
判定
归纳小结
研究两圆的位置关系可以有两种方法:
数学思想方法:数形结合 等价转化
归纳小结
1、圆心距与与的关系
2、两圆方程组成的方程组解的组数
作 业
课本P114页练习第2题
P115页练习第3,4题
问题1:点与圆的位置关系有哪几种 如何判断
问题2:直线与圆的位置关系有哪几种 如何判断
复习引入
直线
相 交 相 切 相 离
d
r
d
r
d
r
两组实数解
一组实数解
无实数解
复习引入
初中学过的平面几何中,圆与圆的位置关系有几种 我们怎样判断圆与圆的位置关系呢
复习引入
人教B版同步教材名师课件
圆与圆的位置关系
学习目标
学 习 目 标 核心素养
体会几何法 掌握利用圆心与圆心的距离与两圆半径的关系判定圆与圆的位置关系的步骤 数学抽象
数学运算
处理圆与圆相切的问题时,注意内切与外切均属于相切,在不能确定的情况下应分类讨论 数学抽象
数学运算
体会求两圆的公共弦的方法及步骤 数学运算
学习目标
学习目标:
1.理解圆与圆的位置关系的种类.
2.掌握圆与圆的位置关系的代数判断方法与几何判断方法,能够利用上述方法判断两圆的位置关系.
学科核心素养:
通过圆与圆的位置关系的推导,提升逻辑推理、直观想象、数学运算的数学素养.
探究新知
探究新知
探究新知
日环食现象
通过刚才对日全食的观察,想象一下两圆有没有出现公共点 公共点的个数是怎样的
探究新知
观察:平面内的两个圆平移,它们有什么样的位置关系
探究新知
两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离.
外离
思考:这两圆的
位置关系
探究新知
外切
两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫这两个圆外切.这个唯一的公共点叫做切点.
探究新知
两个圆有两个公共点,此时叫做这两个圆相交.
相交
探究新知
两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.这个唯一的公共点叫做切点.
内切
探究新知
两个圆外切和内切统称两个圆相切
探究新知
两个圆没有公共点,并且一个圆上的点在另一个圆的内部时叫做这两个圆内含.
内含
两圆同心是两圆内含的一种特例
探究新知
在图中有两圆的多种位置关系,请你找出还没有的位置关系是 .
相交
探究新知
分别观察两圆R、r和d有何数量关系
两圆外切
d=R+r
两圆内切
d=R r(R>r)
两圆外离
d>R+r
两圆内含
d
O2
O1
R
r
d
o1
o2
R
r
d
O1
O2
d
R
r
R
d
r
O1
O2
探究新知
思考:两圆相交时,它们的数量关系如何
两圆相交
R r
探究新知
O1
O2
R
r
d
A
O1
O2
R
r
d
两圆的位置关系的数量特征
两圆外离
两圆外切
定义:连接两圆圆心的线段的长度叫做两圆的圆心距,一般记为d.
d=R+r
d=R r
两圆内含
R r
两圆内切
d>R+r
d
位置关系 d 和R、 r关系 交点
两圆外离 d >R+ r 0
两圆外切 d =R+ r 1
两圆相交 R r
两圆内含 R r >d 0
性质
判定
0
R―r
R+r
同心圆
内含
外离
外切
相交
内切
位 置 关 系 数 字 化
d
探究新知
两圆位置关系的性质与判定
1、通过两圆圆心的直线叫做连心线.
2、两圆圆心之间的距离简称为圆心距.
探究新知
相切两圆的性质
圆是轴对称图形,两个圆是否也组成一个轴对称图形
我们发现通过两圆圆心的直线(连心线)是它的对称轴.
两圆相切时,由于切点是它们唯一的公共点,所以切点一定在对称轴上.
如果两圆相切,那么连心线必过切点
O1
O2
T
O1
O2
经过两圆圆心的直线叫做连心线
探究新知
两圆的对称性
思考:两圆相交时,它们的连心线与公共弦的关系
O1
O2
A
O1
O2
相交两圆的连心线垂直平分公共弦
探究新知
定理 两圆相交时,连心线垂直平分两圆的公共弦
定理 两圆相切时,连心线通过切点
探究新知
法一:圆C1与圆C2的方程联立,得到方程组,① ②,得 x+2y 1=0, ③
由③,得.把上式代入①,并整理,得④
方程④的判别式
所以,方程④有两个不相等的实数根x1,x2分别代入方程③,得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).所以圆C1与圆C2相交.
典例讲解
解析
例1 设圆C1:x2+y2+2x+8y 8=0,圆C2:x2+y2 4x 4y 2=0,试判断圆C1与圆C2的关系.
典例讲解
解析
例1 设圆C1:x2+y2+2x+8y 8=0,圆C2:x2+y2 4x 4y 2=0,试判断圆C1与圆C2的关系.
而
所以圆C1与圆C2相交.
法二: 把圆C1的方程化为标准方程,得
圆C1的圆心是点( 1, 4),半径长r1=5.
把圆C2的方程化为标准方程,得
圆C2的圆心是点(2,2),半径长r2=.
圆C1与圆C2的连心线长为
又
变式训练
1.判断圆C1: x2+y2+4x+8y 5=0与圆C2: x2+y2 4x+4y 1=0的位置关系.
由已知,得C1( 2, 4) , r1=5 , C2( 2, 2) , r2=3 ,
则d=|C1C2|=2=|r1 r2| , ∴两圆内切.
解析
2.两点到直线的距离分别是和5,满足条件的直线共有多少条
y
A
B
O
.
.
(2,2)
( 1, 4)
x
变式训练
典例讲解
(1),, ,
由题意知,,解得或.
(2)设所求圆的方程为,
由圆与直线相切、半径为4,则圆心的坐标为或.
已知圆的圆心的坐标为(2,1),半径为3.
由两圆相切,则或.
例2、(1)圆与相外切,则的值是____________________.
(2)求半径为4,与圆相切,且和直线相切的圆的方程.
或
解析
典例讲解
例2、(1)圆与相外切,则的值是____________________.
(2)求半径为4,与圆相切,且和直线相切的圆的方程.
或
解析
①当圆心为时,或
(无解),故可得,故所求圆的方程为
或.
②当圆心为时,或
(无解),解得.故所求圆的方程为或.
典例讲解
例2、(1)圆与相外切,则的值是____________________.
(2)求半径为4,与圆相切,且和直线相切的圆的方程.
或
解析
综上所述,所求圆的方程为或或.
方法归纳
处理两圆相切问题的两个步骤
(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须分两圆内切还是外切两种情况讨论.
(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值(内切时)或两圆半径之和(外切时).
变式训练
已知圆的方程可化为,则圆心为C(1,0),半径为1.
设所求圆的方程为.
由题意,可得解得或
即所求圆的方程为或
3.求与圆外切且与直线相切于点的圆的方程.
解析
典例讲解
(1)设两圆交点为,,则两点坐标
是方程组的解.① ②,得.
∵ 两点坐标都满足此方程,
∴ 即为两圆公共弦所在直线的方程.
例3、已知圆.
(1)求两圆公共弦所在直线的方程;
(2)求经过两圆交点且圆心在直线上的圆的方程.
解析
典例讲解
例3、已知圆.
(1)求两圆公共弦所在直线的方程;
(2)求经过两圆交点且圆心在直线上的圆的方程.
解析
(2)法一:解方程组得两圆的交点, .
设所求圆的圆心为因圆心在直线上,故.
则,
解得,故圆心为,半径为.
故圆的方程为,即
典例讲解
例3、已知圆.
(1)求两圆公共弦所在直线的方程;
(2)求经过两圆交点且圆心在直线上的圆的方程.
解析
法二:设所求圆的方程为
其圆心为,代入,解得.故所求圆的方程为
方法归纳
1.求两圆公共弦长的方法
一是联立两圆方程求出交点坐标,再用距离公式求解;
二是先求出两圆公共弦所在的直线方程,再利用半径长、弦心距和弦长的一半构成的直角三角形求解.
2.过两圆的交点的圆的方程
已知圆与圆相交,则过两圆交点的圆的方程可设为
变式训练
由例题解析知道是公共弦所在的直线的方程.
因圆的圆心, .
到直线的距离.
∵ 即两圆的公共弦长为
弦的中垂线也就是所在的直线.
∵ ,.
∴的中垂线方程为即.
4.在本例条件不变时,求两圆的公共弦长及公共弦的中垂线的方程.
解析
变式训练
根据条件可知,所求的圆就是以为直径的圆.
∵ 所在直线方程为
所在直线方程为.
∴由得圆心,
又∵ , ∴半径 ,
故所求圆的方程为.
5.本例条件不变,求过两圆的交点且半径最小的圆的方程.
解析
(1)设圆O1:x2+y2+D1x+E1y+F1=0,圆O2:x2+y2+D2x+E2y+F2=0.
则两圆相交公共弦所在直线方程为:
(x2+y2+D1x+E1y+F1) (x2+y2+D2x+E2y+F2)=0,
即(D1 D2)x+(E1 E2)y+(F1 F2)=0.
两圆相交时公共弦问题
素养提炼
两圆相交时公共弦问题
素养提炼
(2)求两圆的公共弦长问题可转化为直线与圆相交求相交弦长问题,从而得以解决,如图,利用圆O1,首先求出O1点到相交弦所在直线的距离d,而所以即,从而得以解决.
当堂练习
将圆的一般方程化为标准方程,
,∴ , , , .
从而 ,∴ .
因此两圆的位置关系为相交.故选C.
1. 圆与的位置关系是( )
A.外离 B.外切 C.相交 D.内含
C
解析
的垂直平分线过两圆的圆心,把圆心代入,即可排除A,B,D.故选C.
2.圆和圆交于两点,则的垂直平分线的方程是( )
A.B. C.D.
解析
C
当堂练习
, ,两圆半径均为1,∵,∴ 的最小值为.
3.已知点在圆上运动,点在圆上运动,则的最小值为_____.
解析
设所求圆的方程为把原点代入可得,所以,即可得过圆与圆的两个交点且过原点O的圆的方程为:.
4.已知圆,,则过圆与圆的两个交点且过原点O的圆的方程为________________.
解析
当堂练习
设圆的半径为,圆心距为,
当圆与圆外切时, , ,
当圆与圆内切时, , ,
圆的方程为或.
5.已知以为圆心的圆与圆: 相切,求圆的方程.
解析
说说这节课你的收获吧!
位置关系 图形 交点个数
外离
内含
外切
相离
相交
内切
相切
0
2
1
d>R+r
0 ≤ d<R r
R r <d<R+r
d=R+r
d=R r
圆与圆的位置关系 数量关系
思想方法:类比方法与分类讨论
性质
判定
归纳小结
研究两圆的位置关系可以有两种方法:
数学思想方法:数形结合 等价转化
归纳小结
1、圆心距与与的关系
2、两圆方程组成的方程组解的组数
作 业
课本P114页练习第2题
P115页练习第3,4题
