人教版七年级上册 第三章 《一元一次方程》全章总复习(32张ppt)
文档属性
| 名称 | 人教版七年级上册 第三章 《一元一次方程》全章总复习(32张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-09 22:03:32 | ||
图片预览











文档简介
(共32张PPT)
第三章一元一次方程全章总复习
人教版七年级上册
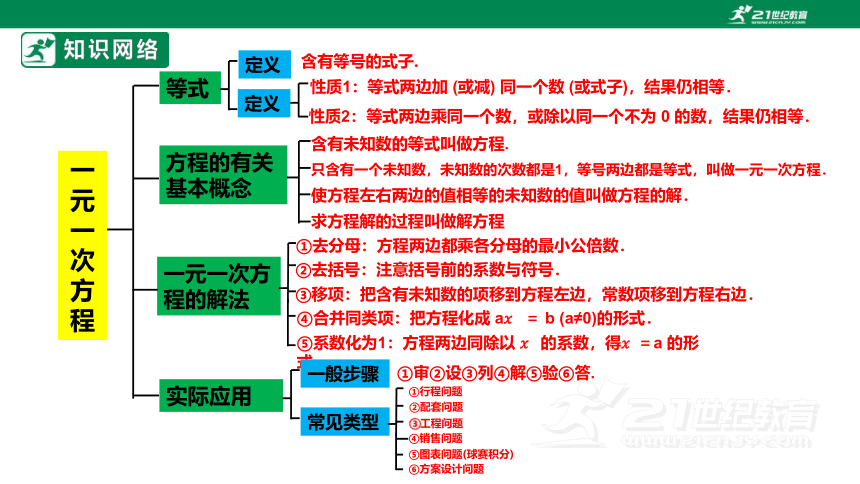
知识网络
一元一次方程
等式
方程的有关基本概念
一元一次方程的解法
实际应用
性质1:等式两边加 (或减) 同一个数 (或式子),结果仍相等.
性质2:等式两边乘同一个数,或除以同一个不为 0 的数,结果仍相等.
定义
定义
含有等号的式子.
含有未知数的等式叫做方程.
只含有一个未知数,未知数的次数都是1,等号两边都是等式,叫做一元一次方程.
使方程左右两边的值相等的未知数的值叫做方程的解.
求方程解的过程叫做解方程
①去分母:方程两边都乘各分母的最小公倍数.
⑤系数化为1:方程两边同除以 的系数,得 =a 的形式.
④合并同类项:把方程化成 a = b (a≠0)的形式.
③移项:把含有未知数的项移到方程左边,常数项移到方程右边.
②去括号:注意括号前的系数与符号.
一般步骤
常见类型
①审②设③列④解⑤验⑥答.
①行程问题
③工程问题
④销售问题
⑤图表问题(球赛积分)
⑥方案设计问题
②配套问题
例1若3 3k 5= 2是关于 的一元一次方程,则k值.
分析:利用一元一次方程的定义得,未知数最高次项次数=1且未知数最高次项系数≠0,据此可得到关于k的一元一次方程,解方程求出k的值.未知数最高次项次数=1且未知数最高次项系数≠0.
解:依题意得:3k 5=1,
解得k=2
所以k的值是2.
考点一:一元一次方程的有关概念
典型例题
考点二:等式的基本性质
运用等式性质进行的变形,正确的是( ).
A A. 如果 , 那么
B. 如果 , 那么
C. 如果 , 那么
D. 如果 , 那么
A
典型例题
考点三:一元一次方程的解法
例3(1)解方程:4( 1)=1
分析:去括号→移项→合并同类项→系数化为1
去括号得:4 4=1
移项得:4 + =1+4
合并同类项,得5 =5
系数化为1,得 =1
(1)解:5( 5)+2 = 4
典型例题
(2)解方程:
分析:解一元一次方程的一般步骤是:去分母→去括号→移项→合并同类项→系数化为1
解:去分母,得 2( +1) (5 1)=6
去括号,得 2 +2 5 +1=6
移项,得 2 5 =6 1 2
合并同类项,得 3 =3
系数化为1 ,得 = 1
典型例题
例4. 2020年3月,我县新冠肺炎疫情最为严重.为支持抗疫,某工厂紧急加工一批医用口罩.已知某车间有52名工人,每名工人每天可以生产800个口罩面或1000个口罩耳绳,一个口罩面需要配2个口罩耳绳.请问安排多少名工人生产口罩面,能使每天生产的口罩面与口罩耳绳刚好配套.
典型例题
考点四:一元一次方程的实际应用
分析:设安排 名工人生产口罩面,能使每天生产的口罩面与口罩耳绳刚好配套,则生产口罩耳绳的工人有(52 )名,根据题意列出方程2×800 =1000(52 ),再求出 的值即可.
典型例题
解:设安排 名工人生产口罩面,能使每天生产的口罩面与口罩耳绳刚好配套,则生产口罩耳绳的工人有(52 )名,
答:安排20名工人生产口罩面,能使每天生产的口罩面与口罩耳绳刚好配套.
解得 =20
依题意得2×800 =1000(52 )
例5 一项工作,甲单独做8天完成,乙单独做12天完成,丙单独做24天完成.现甲、乙合作3天后,甲因有事离去,由乙、丙合作,则乙、丙还要几天才能完成这项工作?
解:设乙、丙还要 天才能完成这项工作,根据题意,得
答:乙、丙还要3天才能完成这项工作.
典型例题
例6 为鼓励学生参加体育锻炼.学校计划拿出不超过1600元的资金再购买一批篮球和排球.已知篮球和排球的单价比为3:2,单价和为80元.
(1)篮球和排球的单价分别是多少元
(2)若要求购买的篮球和排球的总数量是36个,且购买的篮球数量不少于26个.请探究有哪几种购买方案
典型例题
解:(1)设篮球和排球的单价分别为3 元和2 元,依题意,得
3 +2 =80
解得 =16
即 3 =48,2 =32
答:篮球和排球的单价分别为48元和32元
典型例题
(2)采用列表法探索:
篮球( 个) 排球(36 )个 合计(元)
方案1 26
方案2 27
方案3 28
方案4 29
类型
方案
由列表可知,共有三种购买方案:
方案一:购买篮球26个,排球10个;
方案二:购买篮球27个,排球9个;
方案三:购买篮球28个,排球8个.
10
9
8
7
1568
1584
1600
1616
典型例题
1. 在 =1、 =2、 =3中, 是方程2 6=0的解.
2.下列说法正确的是( ).
A = 1是2 2=0的解 B =3是 3=0的解
C = 3是2 +6=0的解 D = 3是2 6=0的解
3.已知3是关于 的方程2 b=1的解,则b的值是( ).
A 5 B 5 C 7 D 2
4.若 =2是关于 的方程2 7= 2+a的解,则 a2022= .
=3
C
B
1
课堂演练
5. 下列运用等式的性质,变形正确的是( ).
A 若 a = b,则 a 3 = b+3
B 若 a = b,则 ac = bc
C 若 ,则 4a = 5b
D 若 = y,则
B
课堂演练
6. 下列说法正确的是( ).
A 3 +2 = 3+2 变形得到 = 1
B 2 = 3 变形得到 2 = 3
C 将方程2a=3系数化为1,得a=3
D 将方程 3 = 4 4 变形得到 = 4
D
课堂演练
课堂演练
7. 某环卫公司有一笔购买新能源汽车的专项资金.据了解,这批资金若买17辆新能源汽车则还差43万元,若买15辆新能源汽车则还剩29万元,若设每辆新能源汽车 万元,则下列方程正确的是( ).
A. 17 +43=15 29 B.
C. 17 43=15 +29 D.
C
课堂演练
8. 下列说法不正确的是( )
A. 在等式ab=ac两边都除以a,可得b=c
B. 在等式a=b两边都除以c2+1,可得
C. 在等式两边乘以a,可得b=2c
D. 在等式2 =2a 4b两边都除以2,可得 =a 2b
A
课堂演练
9. 若关于 的一元一次方程的解是 = 1,则k的值是( )
A. B. C. 1 D. 0
10. 关于y的方程ay 2=4与方程y 1=1的解相同,则a的值是( )A. 2 B. 3 C. 4 D. 2
C
B
课堂演练
11. 小明解方程的步骤如下:
解:方程两边同乘6,得3( +1) 1=2( 2)①
去括号,得3 +3 1=2 2②
移项,得3 2 = 2 3+1③
合并同类项,得 = 4④
以上解题步骤中,开始出错的一步是( )
A. ① B. ② C. ③ D. ④
A
12. 若 (m+5) | m| 4+2=1 是关于 的一元一次方程,求 m的值.
分析:根据一元一次方程的概念,应有未知数 的次数为 1,系数不等于 0.
根据题意,得|m| 4=1且m+5≠0.
由|m| 4=1,解得m=5或m= 5.
由m+5≠0得m≠ 5.
所以m=5.
课堂演练
13. 小明从家里骑自行车到学校,每小时骑15千米,可早到7分钟;每小时骑12千米,就会迟到3分钟,则他家到学校的路程是多少千米?
解:设他家到学校的路程是 千米,
依题意得
解得 =10.
答:他家到学校的路程是10 千米.
课堂演练
14.一轮船在甲、乙两码头间往返航行,已知船在静水中速度为18 km/h,水流速度为2 km/h,往返一次共用9h,求甲、乙两码头之间的距离.
解:设甲、乙两码头之间的距离是 km.
由顺水航行时间+逆水航行时间=往返一次共用时间,得
解得 = 80
答:甲、乙两码头之间的距离是 80 km.
课堂演练
(1)4(2 1) (5 +1)= 8
合并合类项,得
解:去括号,得
8 4 5 1= 8
移项,得
8 5 = 8+4+1
系数化为1,得
3 = 3
15. 解下列方程:
= 1
课堂演练
解:去分母,两边都乘以6,得
去括号,得
移项,得
合并同类项,得
化系数为1 ,得
(2)
6+2( 1)=6 ( +5)
6+2 2=6 5
2 6 + = 5 6+2
3 = 9
=3
课堂演练
16. 2021年1月1日,某社区接种新冠疫苗第二针(分为北京科兴和北京生物两种)人数共110人,其中接种北京科兴的人数是接种北京生物的人数的2倍多20人,求接种两种疫苗的人数分别是多少人?
解:设接种北京生物的人数为 人,则接种北京科兴的人数为(2 +20)人,根据题意
+(2 + 20) =110
解得 =30
所以 2 +20= 2×30+20= 80
答:接种北京生制的人数为30人,接种北京科兴的人数为80人.
课堂演练
17.市为保障供水及道路安全,自来水有限公司排查地下管线密集区,决定改造一段已使用多年面临老化的自来水管,这项翻新工程如果由甲工程队单独改造需要12天,由乙工程队单独改造需要24天.现要求甲、乙两个工程队一起合作完成这项翻新工程,但由于工作调动的原因,该项工程完工时,乙工程队中途共离开了3天,问这项工程一共用了多少天?
课堂演练
分析: 设这项工程一共用了 天, 根据甲独干工作量+乙独干工作量=工作总量,列出方程并解之即可.
设这项工程一共用了 天,根据题意,得
解得 = 9
答:这项工程一共用了9天.
课堂演练
解:∵甲工程队单独改造需要12天,由乙工程队单独改造需要24天,
∴甲的工作效率为: ,乙的工作效率为:
18. 某商店有两种书包,每个小书包比大书包的进价少10元,而它们的售后利润额相同.其中,每个小书包的盈利率为30% , 每个大书包的盈利率为20% , 试求两种书包的进价.
解:设每个小书包的进价为 元,则每个大书包的进价为( +10)元,根据题意得
30% =20%( +10)
答:每个小书包的进价为20元,每个大书包的进价为30元.
课堂演练
解得: =20
则 +10=30
19. 为了积极配合学校开展的“阳光体育”活动,七(1)班同学准备购买一些乒乓球和乒乓球拍,每副球拍30元,每盒乒乓球5元,甲、乙两商店又推出不同的优惠方案:甲商店买一副球拍赠送1盒乒乓球;乙商店全部按定价的9折优惠。同学们需要球拍5副,乒乓球若干盒(不小于5盒),问:
(1)当购买乒乓球多少盒时,到两家商店花钱一样多?
(2)若同学们需要15盒乒乓球,请你去办这件事,你决定去哪家商店购买
课堂演练
(1)解:设当购买乒乓球 盒时,到两家商店花钱一样多,由题意得:
(5×30+5 )×0.9=5×30+5( 5)
答:当购买乒乓球20盒时,到两家商店花钱一样多.
解得 =20
(2)解:甲商店花钱:(5×30+5×15)×0.9=202.5(元)
乙商店花钱: 5×30+5×(15 5)=200(元)
答:当购买乒乓球15盒时,选乙商店省钱.
课堂演练
复习题3
第111页第2(3)、(4)题
第112第7、8题
课外作业
https://www.21cnjy.com/help/help_e tract.php
第三章一元一次方程全章总复习
人教版七年级上册
知识网络
一元一次方程
等式
方程的有关基本概念
一元一次方程的解法
实际应用
性质1:等式两边加 (或减) 同一个数 (或式子),结果仍相等.
性质2:等式两边乘同一个数,或除以同一个不为 0 的数,结果仍相等.
定义
定义
含有等号的式子.
含有未知数的等式叫做方程.
只含有一个未知数,未知数的次数都是1,等号两边都是等式,叫做一元一次方程.
使方程左右两边的值相等的未知数的值叫做方程的解.
求方程解的过程叫做解方程
①去分母:方程两边都乘各分母的最小公倍数.
⑤系数化为1:方程两边同除以 的系数,得 =a 的形式.
④合并同类项:把方程化成 a = b (a≠0)的形式.
③移项:把含有未知数的项移到方程左边,常数项移到方程右边.
②去括号:注意括号前的系数与符号.
一般步骤
常见类型
①审②设③列④解⑤验⑥答.
①行程问题
③工程问题
④销售问题
⑤图表问题(球赛积分)
⑥方案设计问题
②配套问题
例1若3 3k 5= 2是关于 的一元一次方程,则k值.
分析:利用一元一次方程的定义得,未知数最高次项次数=1且未知数最高次项系数≠0,据此可得到关于k的一元一次方程,解方程求出k的值.未知数最高次项次数=1且未知数最高次项系数≠0.
解:依题意得:3k 5=1,
解得k=2
所以k的值是2.
考点一:一元一次方程的有关概念
典型例题
考点二:等式的基本性质
运用等式性质进行的变形,正确的是( ).
A A. 如果 , 那么
B. 如果 , 那么
C. 如果 , 那么
D. 如果 , 那么
A
典型例题
考点三:一元一次方程的解法
例3(1)解方程:4( 1)=1
分析:去括号→移项→合并同类项→系数化为1
去括号得:4 4=1
移项得:4 + =1+4
合并同类项,得5 =5
系数化为1,得 =1
(1)解:5( 5)+2 = 4
典型例题
(2)解方程:
分析:解一元一次方程的一般步骤是:去分母→去括号→移项→合并同类项→系数化为1
解:去分母,得 2( +1) (5 1)=6
去括号,得 2 +2 5 +1=6
移项,得 2 5 =6 1 2
合并同类项,得 3 =3
系数化为1 ,得 = 1
典型例题
例4. 2020年3月,我县新冠肺炎疫情最为严重.为支持抗疫,某工厂紧急加工一批医用口罩.已知某车间有52名工人,每名工人每天可以生产800个口罩面或1000个口罩耳绳,一个口罩面需要配2个口罩耳绳.请问安排多少名工人生产口罩面,能使每天生产的口罩面与口罩耳绳刚好配套.
典型例题
考点四:一元一次方程的实际应用
分析:设安排 名工人生产口罩面,能使每天生产的口罩面与口罩耳绳刚好配套,则生产口罩耳绳的工人有(52 )名,根据题意列出方程2×800 =1000(52 ),再求出 的值即可.
典型例题
解:设安排 名工人生产口罩面,能使每天生产的口罩面与口罩耳绳刚好配套,则生产口罩耳绳的工人有(52 )名,
答:安排20名工人生产口罩面,能使每天生产的口罩面与口罩耳绳刚好配套.
解得 =20
依题意得2×800 =1000(52 )
例5 一项工作,甲单独做8天完成,乙单独做12天完成,丙单独做24天完成.现甲、乙合作3天后,甲因有事离去,由乙、丙合作,则乙、丙还要几天才能完成这项工作?
解:设乙、丙还要 天才能完成这项工作,根据题意,得
答:乙、丙还要3天才能完成这项工作.
典型例题
例6 为鼓励学生参加体育锻炼.学校计划拿出不超过1600元的资金再购买一批篮球和排球.已知篮球和排球的单价比为3:2,单价和为80元.
(1)篮球和排球的单价分别是多少元
(2)若要求购买的篮球和排球的总数量是36个,且购买的篮球数量不少于26个.请探究有哪几种购买方案
典型例题
解:(1)设篮球和排球的单价分别为3 元和2 元,依题意,得
3 +2 =80
解得 =16
即 3 =48,2 =32
答:篮球和排球的单价分别为48元和32元
典型例题
(2)采用列表法探索:
篮球( 个) 排球(36 )个 合计(元)
方案1 26
方案2 27
方案3 28
方案4 29
类型
方案
由列表可知,共有三种购买方案:
方案一:购买篮球26个,排球10个;
方案二:购买篮球27个,排球9个;
方案三:购买篮球28个,排球8个.
10
9
8
7
1568
1584
1600
1616
典型例题
1. 在 =1、 =2、 =3中, 是方程2 6=0的解.
2.下列说法正确的是( ).
A = 1是2 2=0的解 B =3是 3=0的解
C = 3是2 +6=0的解 D = 3是2 6=0的解
3.已知3是关于 的方程2 b=1的解,则b的值是( ).
A 5 B 5 C 7 D 2
4.若 =2是关于 的方程2 7= 2+a的解,则 a2022= .
=3
C
B
1
课堂演练
5. 下列运用等式的性质,变形正确的是( ).
A 若 a = b,则 a 3 = b+3
B 若 a = b,则 ac = bc
C 若 ,则 4a = 5b
D 若 = y,则
B
课堂演练
6. 下列说法正确的是( ).
A 3 +2 = 3+2 变形得到 = 1
B 2 = 3 变形得到 2 = 3
C 将方程2a=3系数化为1,得a=3
D 将方程 3 = 4 4 变形得到 = 4
D
课堂演练
课堂演练
7. 某环卫公司有一笔购买新能源汽车的专项资金.据了解,这批资金若买17辆新能源汽车则还差43万元,若买15辆新能源汽车则还剩29万元,若设每辆新能源汽车 万元,则下列方程正确的是( ).
A. 17 +43=15 29 B.
C. 17 43=15 +29 D.
C
课堂演练
8. 下列说法不正确的是( )
A. 在等式ab=ac两边都除以a,可得b=c
B. 在等式a=b两边都除以c2+1,可得
C. 在等式两边乘以a,可得b=2c
D. 在等式2 =2a 4b两边都除以2,可得 =a 2b
A
课堂演练
9. 若关于 的一元一次方程的解是 = 1,则k的值是( )
A. B. C. 1 D. 0
10. 关于y的方程ay 2=4与方程y 1=1的解相同,则a的值是( )A. 2 B. 3 C. 4 D. 2
C
B
课堂演练
11. 小明解方程的步骤如下:
解:方程两边同乘6,得3( +1) 1=2( 2)①
去括号,得3 +3 1=2 2②
移项,得3 2 = 2 3+1③
合并同类项,得 = 4④
以上解题步骤中,开始出错的一步是( )
A. ① B. ② C. ③ D. ④
A
12. 若 (m+5) | m| 4+2=1 是关于 的一元一次方程,求 m的值.
分析:根据一元一次方程的概念,应有未知数 的次数为 1,系数不等于 0.
根据题意,得|m| 4=1且m+5≠0.
由|m| 4=1,解得m=5或m= 5.
由m+5≠0得m≠ 5.
所以m=5.
课堂演练
13. 小明从家里骑自行车到学校,每小时骑15千米,可早到7分钟;每小时骑12千米,就会迟到3分钟,则他家到学校的路程是多少千米?
解:设他家到学校的路程是 千米,
依题意得
解得 =10.
答:他家到学校的路程是10 千米.
课堂演练
14.一轮船在甲、乙两码头间往返航行,已知船在静水中速度为18 km/h,水流速度为2 km/h,往返一次共用9h,求甲、乙两码头之间的距离.
解:设甲、乙两码头之间的距离是 km.
由顺水航行时间+逆水航行时间=往返一次共用时间,得
解得 = 80
答:甲、乙两码头之间的距离是 80 km.
课堂演练
(1)4(2 1) (5 +1)= 8
合并合类项,得
解:去括号,得
8 4 5 1= 8
移项,得
8 5 = 8+4+1
系数化为1,得
3 = 3
15. 解下列方程:
= 1
课堂演练
解:去分母,两边都乘以6,得
去括号,得
移项,得
合并同类项,得
化系数为1 ,得
(2)
6+2( 1)=6 ( +5)
6+2 2=6 5
2 6 + = 5 6+2
3 = 9
=3
课堂演练
16. 2021年1月1日,某社区接种新冠疫苗第二针(分为北京科兴和北京生物两种)人数共110人,其中接种北京科兴的人数是接种北京生物的人数的2倍多20人,求接种两种疫苗的人数分别是多少人?
解:设接种北京生物的人数为 人,则接种北京科兴的人数为(2 +20)人,根据题意
+(2 + 20) =110
解得 =30
所以 2 +20= 2×30+20= 80
答:接种北京生制的人数为30人,接种北京科兴的人数为80人.
课堂演练
17.市为保障供水及道路安全,自来水有限公司排查地下管线密集区,决定改造一段已使用多年面临老化的自来水管,这项翻新工程如果由甲工程队单独改造需要12天,由乙工程队单独改造需要24天.现要求甲、乙两个工程队一起合作完成这项翻新工程,但由于工作调动的原因,该项工程完工时,乙工程队中途共离开了3天,问这项工程一共用了多少天?
课堂演练
分析: 设这项工程一共用了 天, 根据甲独干工作量+乙独干工作量=工作总量,列出方程并解之即可.
设这项工程一共用了 天,根据题意,得
解得 = 9
答:这项工程一共用了9天.
课堂演练
解:∵甲工程队单独改造需要12天,由乙工程队单独改造需要24天,
∴甲的工作效率为: ,乙的工作效率为:
18. 某商店有两种书包,每个小书包比大书包的进价少10元,而它们的售后利润额相同.其中,每个小书包的盈利率为30% , 每个大书包的盈利率为20% , 试求两种书包的进价.
解:设每个小书包的进价为 元,则每个大书包的进价为( +10)元,根据题意得
30% =20%( +10)
答:每个小书包的进价为20元,每个大书包的进价为30元.
课堂演练
解得: =20
则 +10=30
19. 为了积极配合学校开展的“阳光体育”活动,七(1)班同学准备购买一些乒乓球和乒乓球拍,每副球拍30元,每盒乒乓球5元,甲、乙两商店又推出不同的优惠方案:甲商店买一副球拍赠送1盒乒乓球;乙商店全部按定价的9折优惠。同学们需要球拍5副,乒乓球若干盒(不小于5盒),问:
(1)当购买乒乓球多少盒时,到两家商店花钱一样多?
(2)若同学们需要15盒乒乓球,请你去办这件事,你决定去哪家商店购买
课堂演练
(1)解:设当购买乒乓球 盒时,到两家商店花钱一样多,由题意得:
(5×30+5 )×0.9=5×30+5( 5)
答:当购买乒乓球20盒时,到两家商店花钱一样多.
解得 =20
(2)解:甲商店花钱:(5×30+5×15)×0.9=202.5(元)
乙商店花钱: 5×30+5×(15 5)=200(元)
答:当购买乒乓球15盒时,选乙商店省钱.
课堂演练
复习题3
第111页第2(3)、(4)题
第112第7、8题
课外作业
https://www.21cnjy.com/help/help_e tract.php
