人教版小学数学六年级上册6.《百分数(一)应用题中的几种思想》课件 (共25张PPT)
文档属性
| 名称 | 人教版小学数学六年级上册6.《百分数(一)应用题中的几种思想》课件 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 632.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-08 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
百分数(分数)应用题
的几种思想
方程思想
解决分数(百分数)应用题中求单位1的数量时,往往会根据题目中的数量关系,列方程解决这一类的问题
例题1:收集的风景图片占60%,人物图片占30%,风景图片比人物图片多15张。一共收集了多少张图片
解:设一共收集了x 张图片。
60%x-30%x=15
x=50
答:一共收集了50张图片。
风景图片-人物图片=15
例题2. 2011年末全国私人汽车保有量是7872 万辆,比2010年末增长20.4%。2010年末全国私人汽车保有量大约是多少万辆?(得数保留整数)
解:设2010年末全国私人汽车保有量
大约是x万辆。
(1+20.4%)x=7872
x≈6538
答:2010年末全国私人汽车保有量大约是6538万辆。
单位“1”
1.一桶油,第一次吃去 ,第二次吃去这桶油的40%,第一次比第二次多吃2千克。这桶油共重多少千克?
2.一辆汽车从甲地开往乙地,已经行了全程的35%,比余下的路程少60km,甲、乙两地相距多少km?
量率对应
“量率对应”是分数(百分数)应用题的一大特点,即对于同一个单位“1”的量,每一个具体数量,都有一个相对应的分率.
所有分数应用题都源于最基本的数量关系:一个数的几分之几是多少。
基本数量关系式为 :
单位“1”X 对应分率=对应数量;
对应数量÷单位“1”=对应分率;
对应数量÷对应分率=单位“1”。
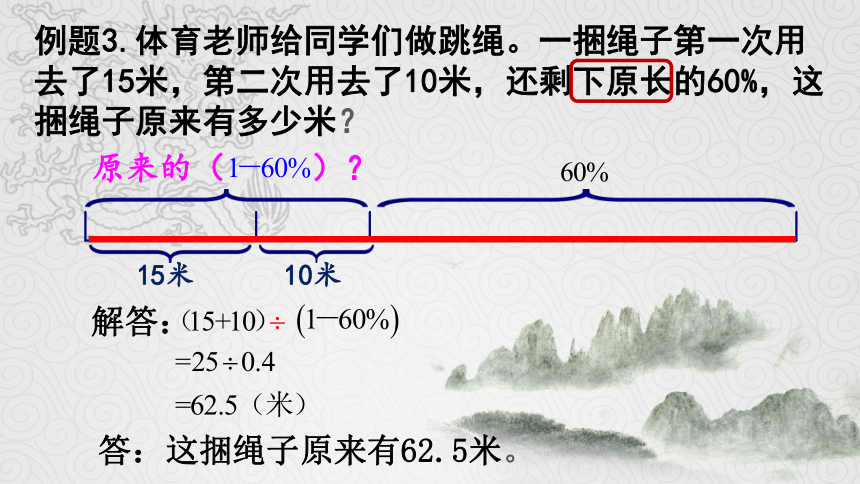
例题3.体育老师给同学们做跳绳。一捆绳子第一次用去了15米,第二次用去了10米,还剩下原长的60%,这捆绳子原来有多少米?
15米
10米
原来的( )?
解答:
答:这捆绳子原来有62.5米。
1.李老师有一批新书发给同学们,给一班的孩子发了45本,给二班的孩子发了50本,还剩下全部的5%,请问原来一共有多少新书
2.小明有一些零用钱,第一天用了45元,第二天用了原来的20%,还剩下35元,小明原来有多少零用钱
1.李老师有一批新书发给同学们,给一班的孩子发了45本,给二班的孩子发了50本,还剩下全部的5%,请问原来一共有多少新书
(45+50)÷(1-5%)
=95÷95%
=100(本)
答:原来一共有100本新书。
2.小明有一些零用钱,第一天用了45元,第二天用了原来的20%,还剩下35元,小明原来有多少零用钱
(45+35)÷(1-20%)
=80÷80%
=100(元)
答:小明原来有100元零用钱。
例4:某工厂由于采用了新工艺,现在每件产品的成本是37.4元,比原来降低了15%,原来每件产品的成本是多少元?
现在每件的成本对应的分率是多少呢?
37.4÷(1-15%)
=37.4÷85%
=44(元)
单位“1”
答:原来每件产品的成本是44元。
1.商场有一种衣服的售价为34元,比原来的定价便宜15%,原价多少元?
2.六年级学生去植树,男生植树320棵,比女生多植25%。男生比女生多植了多少棵?
34÷(1-15%)
=34÷85%
=40(元)
答:原价40元。
女生植树:320÷(1+25%)
=320÷125%
=256(棵)
答:男生比女生多植了64棵。
320-256=64(棵)
例5:小红家和小强家一共有果树198棵,小强家比小红家多20%。小红家和小强家各有果树多少棵?
将小红家果树看做单位“1”,根据小强家比小红家多20%,知道:小强家-小红家=小红家×20%,故小强家果树可以用小红家表示出来:小强家=小红家×(1+20%)。
分析:因为小强家=小红家×(1+20%),一共的果树
等于小强家+小红家,即
一共的果树=小红家×( )。
解答:小红家:
小强家:
答:小红家有果树90棵,小强家有果树108棵。
例5:小红家和小强家一共有果树198棵,小强家比小红家多20%。小红家和小强家各有果树多少棵?
1.优优和小奥一共折了36只纸鹤,优优折的比小奥折的多40%,优优和小奥各折了多少只纸鹤?
小奥:36÷(1+40%+1)
=36÷2.4
=15(只)
答:优优折了21只纸鹤,小奥折了15只纸鹤。
优优:36-15=21(只)
技巧点拨:
做较复杂的百分数应用题,一般有多个单位“1”,理清量率对应关系,将多个单位“1”转化为同一个单位“1”。
某服装店销售一件大衣1000元,因滞销降价10%,后因旺季提价10%,这件大衣是涨价还是降价了?现价是多少元?
1000 ×(1-10%)×(1+10%)
=1000×0.9×1.1
=990(元)
答:这件大衣是降价了,现价是990元。
1000元>990元
变一下
某服装店销售一件大衣,因滞销降价10%,后因旺季提价10%,这件大衣是涨价还是降价了?
1000 ×(1-10%)×(1+10%)
=1000×0.9×1.1
=990(元)
答:这件大衣是降价了。
1000元>990元
变一下
某服装店销售一件大衣,因滞销降价10%,后因旺季提价10%,这件大衣是涨价还是降价了?
1 ×(1-10%)×(1+10%)
=1×0.9×1.1
=0.99
答:这件大衣是降价了
1>0.99
有关变化幅度的问题
常用假设法。
(1)假设单位“1”的量为某一个具体的数。
(2)假设单位“1”的量为1或a等,假设单
位“1”的量是1计算更简便。
1.选一选。
(1)昨天的平均气温比前天升高了6%,今天
的平均气温比昨天降低了6%,今天的平均气
温与前天相比,( )。
A.升高了 B.降低了 C.没有变化
(2)一袋大米重50kg,吃掉20%,再增加
20%,这袋大米现在重( )。
A.48kg B.50kg C.52kg
B
A
(3)某种蔬菜去年3月第一周比上一周涨价
5%,第二周比第一周涨价5% 。两周以来
共涨价( )。
假设上一周价格为1元。
第一周:1×(1+5%)=1.05(元)
第二周:1.05×(1+5%)=1.1025(元)
共涨价:(1.1025-1)÷1=0.1025=10.25%
C
A.10% B.5% C.10.25%
2.某电视机厂计划某种型号的电视机比去年增产
50%,实际又比计划的产量多生产了10%。此
型号的电视机今年的实际产量是去年的百分之
多少?
答:今年的实际产量是去年的165%。
1×(1+50%)×(1+10%)÷1
=1×150%×110%÷1
=165%
单位“1”
单位“1”
1.某商店卖出一件480元的上衣,赚了20%。这件上衣的进价是多少元?
480÷(1+20%)
=480÷1.2
=400(元)
答:这件上衣的进价是400元。
买卖赚亏
2.彩虹服装店将两款不同的服装均以每件240元的价钱出售,结果一件赚了20%,另一件赔了20%。出售这两件衣服,服装店老板是赚了还是亏了?赚(亏)了多少元?
240÷(1+20%)
=240÷1.2
=200(元)
答:服装店老板亏了,亏了20元。
240÷(1-20%)
=240÷0.8
=300(元)
进价:200+300=500(元)
500-240×2=20(元)
百分数(分数)应用题
的几种思想
方程思想
解决分数(百分数)应用题中求单位1的数量时,往往会根据题目中的数量关系,列方程解决这一类的问题
例题1:收集的风景图片占60%,人物图片占30%,风景图片比人物图片多15张。一共收集了多少张图片
解:设一共收集了x 张图片。
60%x-30%x=15
x=50
答:一共收集了50张图片。
风景图片-人物图片=15
例题2. 2011年末全国私人汽车保有量是7872 万辆,比2010年末增长20.4%。2010年末全国私人汽车保有量大约是多少万辆?(得数保留整数)
解:设2010年末全国私人汽车保有量
大约是x万辆。
(1+20.4%)x=7872
x≈6538
答:2010年末全国私人汽车保有量大约是6538万辆。
单位“1”
1.一桶油,第一次吃去 ,第二次吃去这桶油的40%,第一次比第二次多吃2千克。这桶油共重多少千克?
2.一辆汽车从甲地开往乙地,已经行了全程的35%,比余下的路程少60km,甲、乙两地相距多少km?
量率对应
“量率对应”是分数(百分数)应用题的一大特点,即对于同一个单位“1”的量,每一个具体数量,都有一个相对应的分率.
所有分数应用题都源于最基本的数量关系:一个数的几分之几是多少。
基本数量关系式为 :
单位“1”X 对应分率=对应数量;
对应数量÷单位“1”=对应分率;
对应数量÷对应分率=单位“1”。
例题3.体育老师给同学们做跳绳。一捆绳子第一次用去了15米,第二次用去了10米,还剩下原长的60%,这捆绳子原来有多少米?
15米
10米
原来的( )?
解答:
答:这捆绳子原来有62.5米。
1.李老师有一批新书发给同学们,给一班的孩子发了45本,给二班的孩子发了50本,还剩下全部的5%,请问原来一共有多少新书
2.小明有一些零用钱,第一天用了45元,第二天用了原来的20%,还剩下35元,小明原来有多少零用钱
1.李老师有一批新书发给同学们,给一班的孩子发了45本,给二班的孩子发了50本,还剩下全部的5%,请问原来一共有多少新书
(45+50)÷(1-5%)
=95÷95%
=100(本)
答:原来一共有100本新书。
2.小明有一些零用钱,第一天用了45元,第二天用了原来的20%,还剩下35元,小明原来有多少零用钱
(45+35)÷(1-20%)
=80÷80%
=100(元)
答:小明原来有100元零用钱。
例4:某工厂由于采用了新工艺,现在每件产品的成本是37.4元,比原来降低了15%,原来每件产品的成本是多少元?
现在每件的成本对应的分率是多少呢?
37.4÷(1-15%)
=37.4÷85%
=44(元)
单位“1”
答:原来每件产品的成本是44元。
1.商场有一种衣服的售价为34元,比原来的定价便宜15%,原价多少元?
2.六年级学生去植树,男生植树320棵,比女生多植25%。男生比女生多植了多少棵?
34÷(1-15%)
=34÷85%
=40(元)
答:原价40元。
女生植树:320÷(1+25%)
=320÷125%
=256(棵)
答:男生比女生多植了64棵。
320-256=64(棵)
例5:小红家和小强家一共有果树198棵,小强家比小红家多20%。小红家和小强家各有果树多少棵?
将小红家果树看做单位“1”,根据小强家比小红家多20%,知道:小强家-小红家=小红家×20%,故小强家果树可以用小红家表示出来:小强家=小红家×(1+20%)。
分析:因为小强家=小红家×(1+20%),一共的果树
等于小强家+小红家,即
一共的果树=小红家×( )。
解答:小红家:
小强家:
答:小红家有果树90棵,小强家有果树108棵。
例5:小红家和小强家一共有果树198棵,小强家比小红家多20%。小红家和小强家各有果树多少棵?
1.优优和小奥一共折了36只纸鹤,优优折的比小奥折的多40%,优优和小奥各折了多少只纸鹤?
小奥:36÷(1+40%+1)
=36÷2.4
=15(只)
答:优优折了21只纸鹤,小奥折了15只纸鹤。
优优:36-15=21(只)
技巧点拨:
做较复杂的百分数应用题,一般有多个单位“1”,理清量率对应关系,将多个单位“1”转化为同一个单位“1”。
某服装店销售一件大衣1000元,因滞销降价10%,后因旺季提价10%,这件大衣是涨价还是降价了?现价是多少元?
1000 ×(1-10%)×(1+10%)
=1000×0.9×1.1
=990(元)
答:这件大衣是降价了,现价是990元。
1000元>990元
变一下
某服装店销售一件大衣,因滞销降价10%,后因旺季提价10%,这件大衣是涨价还是降价了?
1000 ×(1-10%)×(1+10%)
=1000×0.9×1.1
=990(元)
答:这件大衣是降价了。
1000元>990元
变一下
某服装店销售一件大衣,因滞销降价10%,后因旺季提价10%,这件大衣是涨价还是降价了?
1 ×(1-10%)×(1+10%)
=1×0.9×1.1
=0.99
答:这件大衣是降价了
1>0.99
有关变化幅度的问题
常用假设法。
(1)假设单位“1”的量为某一个具体的数。
(2)假设单位“1”的量为1或a等,假设单
位“1”的量是1计算更简便。
1.选一选。
(1)昨天的平均气温比前天升高了6%,今天
的平均气温比昨天降低了6%,今天的平均气
温与前天相比,( )。
A.升高了 B.降低了 C.没有变化
(2)一袋大米重50kg,吃掉20%,再增加
20%,这袋大米现在重( )。
A.48kg B.50kg C.52kg
B
A
(3)某种蔬菜去年3月第一周比上一周涨价
5%,第二周比第一周涨价5% 。两周以来
共涨价( )。
假设上一周价格为1元。
第一周:1×(1+5%)=1.05(元)
第二周:1.05×(1+5%)=1.1025(元)
共涨价:(1.1025-1)÷1=0.1025=10.25%
C
A.10% B.5% C.10.25%
2.某电视机厂计划某种型号的电视机比去年增产
50%,实际又比计划的产量多生产了10%。此
型号的电视机今年的实际产量是去年的百分之
多少?
答:今年的实际产量是去年的165%。
1×(1+50%)×(1+10%)÷1
=1×150%×110%÷1
=165%
单位“1”
单位“1”
1.某商店卖出一件480元的上衣,赚了20%。这件上衣的进价是多少元?
480÷(1+20%)
=480÷1.2
=400(元)
答:这件上衣的进价是400元。
买卖赚亏
2.彩虹服装店将两款不同的服装均以每件240元的价钱出售,结果一件赚了20%,另一件赔了20%。出售这两件衣服,服装店老板是赚了还是亏了?赚(亏)了多少元?
240÷(1+20%)
=240÷1.2
=200(元)
答:服装店老板亏了,亏了20元。
240÷(1-20%)
=240÷0.8
=300(元)
进价:200+300=500(元)
500-240×2=20(元)
