5.4平移(第1课时)平移及其性质 课件(共29张PPT)
文档属性
| 名称 | 5.4平移(第1课时)平移及其性质 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 00:00:00 | ||
图片预览



文档简介
(共29张PPT)
人教版 七年级数学下册
第5章 相交线与平行线
5.4 平移
第1课时 平移及其性质
学习目标
1. 通过具体实例认识平移.
2. 探索平移的基本性质.
3. 认识并欣赏平移在自然界和现实生活中的应用.
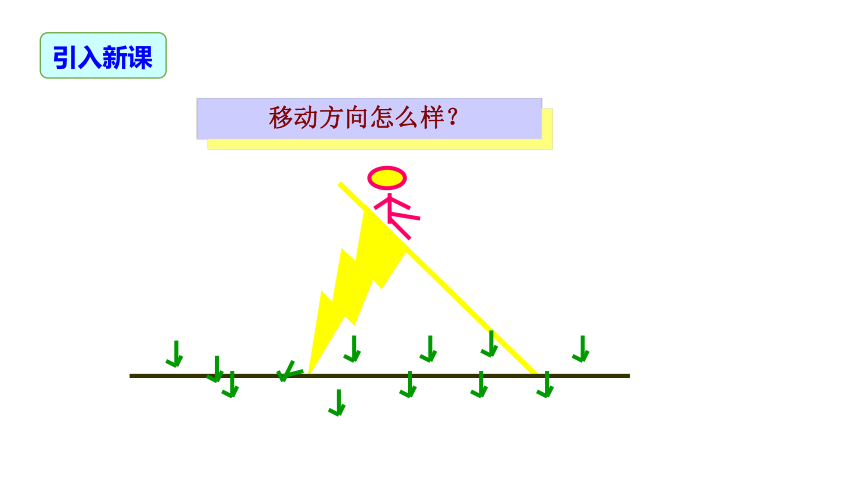
移动方向怎么样?
引入新课
移动方向怎么样?
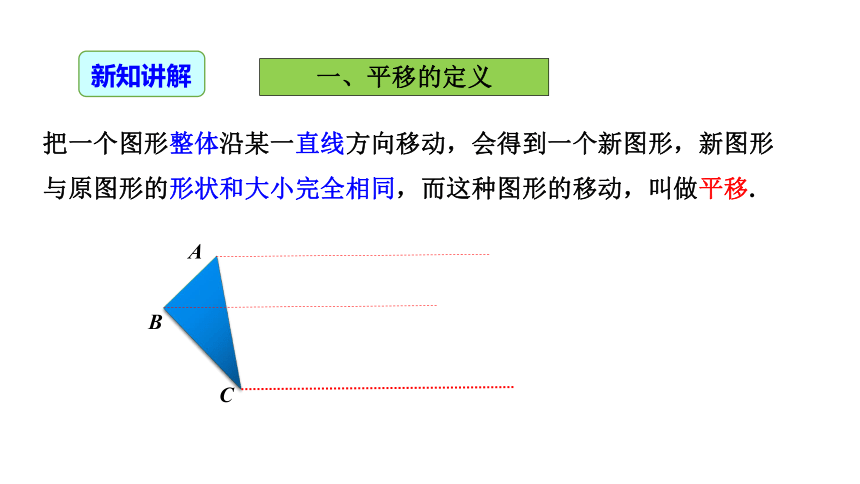
把一个图形整体沿某一直线方向移动,会得到一个新图形,新图形与原图形的形状和大小完全相同,而这种图形的移动,叫做平移.
A
B
C
一、平移的定义
新知讲解
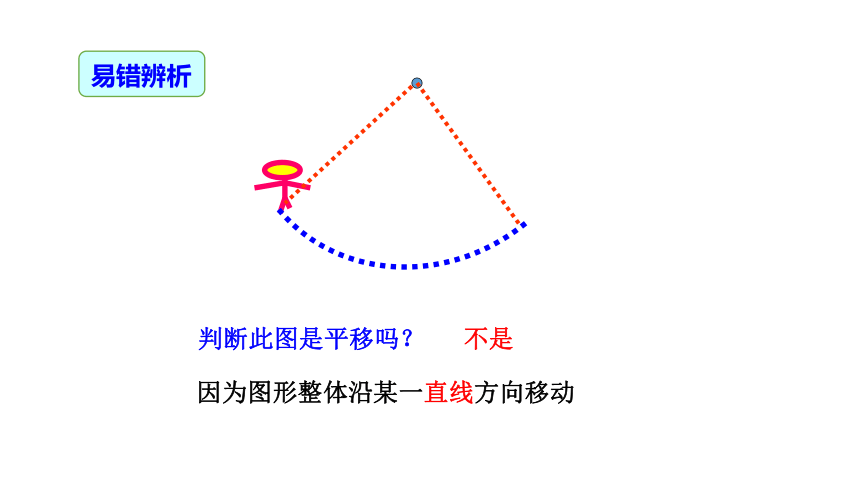
判断此图是平移吗?
不是
因为图形整体沿某一直线方向移动
易错辨析
图形的平移一定是水平或竖直的吗?
图形的平移不一定是水平的,也不一定是竖直的.
如:左图鸟的飞行也是平移
图形平移的路径是直线即可
易错辨析
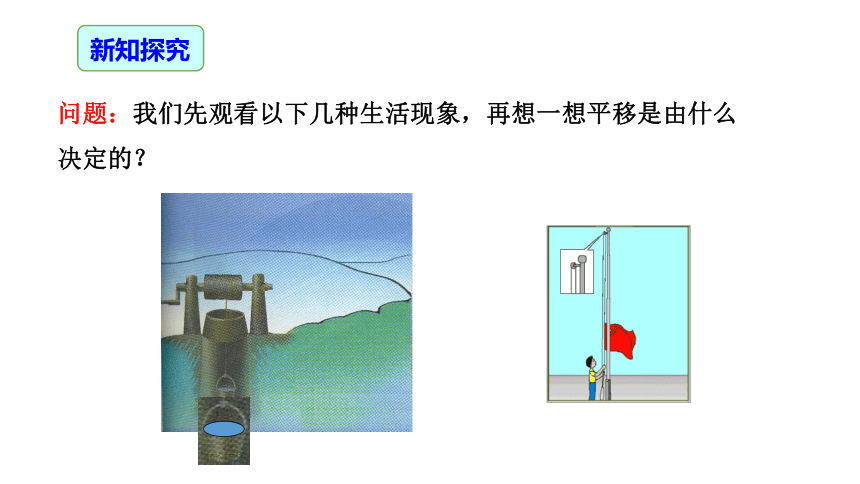
问题:我们先观看以下几种生活现象,再想一想平移是由什么决定的?
新知探究
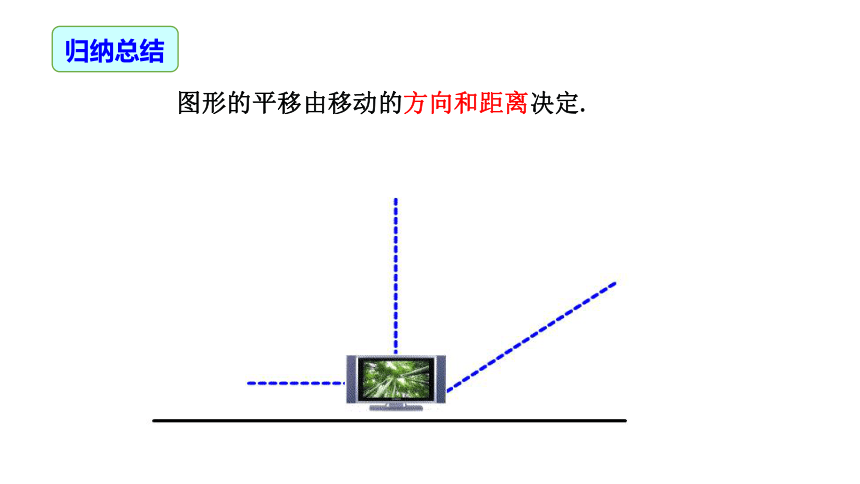
图形的平移由移动的方向和距离决定.
归纳总结
可以把一张半透明的纸盖在图上,先描出第一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个……(如图)
如何在一张纸上画出一排形状和大小如下图的雪人?
新知探究
问:雪人的形状、大小、位置在运动前后是否发生了变化?
答:雪人的形状不变,大小不变,位置改变.
平移不改变图形的形状、大小
平移改变图形的位置
简述为:“一变两不变”
二、平移的基本性质1
新知归纳
1. 下图中的变换属于平移的有哪些?
F
A
B
D
E
C
旋转
轴对称
针对训练
√
2. 下面 2,3,4,5 幅图中哪幅图是由1平移得到的?
1
2
3
4
5
(1)
(2)
2
3
4
5
1
√
√
C
4. 平移改变的是图形的( )
A. 位置 B. 大小
C. 形状 D. 位置、形状和大小
A
区分平移、旋转和轴对称.
易错辨析
甲
乙
雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是怎样运动的?它运动到了什么位置?帽顶B呢?
A运动到A′ ,B运动到B′.
新知探究
甲
乙
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点就是对应点.
可以发现:AA′∥BB′∥CC′并且AA′=BB′=CC′
再作出连接其他对应点的线段,仍有前面的关系吗?
有
B
A
C
A′
B′
C′
连接几组对应点(如:A与A′ ,B与B′ ,C与C′ )观察得到的线段,它们的位置、长短有什么关系?
D
D′
注意:平行线段是指线段所在的直线平行
动动手:用三角板、直尺画平行线.
P
Q
D
E
F
A
B
C
观察:线段AB与DE的位置关系与数量关系.
直尺PQ是倾斜放置,用三角板能否画 出平行线?
AB//DE
AB=DE
注意:在平移过程中,对应线段也可能在一条直线上(如:BC与EF)
经过平移,对应点所连的线段平行且相等
图形中的每一个点都移动了相同的距离
三、平移的基本性质2
新知归纳
1. 在图形平移中,下面说法错误的是( )
A. 图形上任意点移动的方向相同
B. 图形上任意点移动的距离相等
C. 图形上任意两点的连线的长度改变
D. 图形在平移前后形状和大小不发生改变
C
当堂巩固
2. 如图,△ABC平移到△DEF的位置,请回答下列问题.
解:对应点:
点A和___点、点B和__点、点C和__点;
经过平移后,有哪些线段是相等的?
D
E
F
线段AB和____、线段BC和____、线段AC和_____;
DE
EF
DF
1.(4分)(2020 上海6/25)如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
【解答】解:如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
∵四边形ABEF向右平移可以与四边形EFDC重合,
∴平行四边形ABCD是平移重合图形,
故选:A.
感受中考
【解答】解:∵△ABC沿BC边向右平移2个单位,得到△DEF,
∴AD=CF=2,AC=DF,
∵△ABC的周长为8,
∴AB+BC+AC=8,
∴AB+BC+DF=8,
∴四边形ABFD的周长= AB+BC+CF +DF+AD= AB+BC+ DF+AD+CF=8+2+2=12.
故答案为12.
2.(2分)(2020 青海4/28)如图,将周长为8的△ABC沿BC边向右平移2个单位,得到△DEF,则四边形ABFD的周长为 .
感受中考
平移在自然界和现实生活中的应用
工厂里的传输带,电梯等
1. 平移的定义
把一个图形整体沿某一直线方向移动,会得到一个新图形,新图形与原图形的形状和大小完全相同,而这种图形的移动,叫做平移.
2. 平移的基本性质
(1)平移不改变图形的形状、大小,改变图形位置
(2)对应点所连线段平行且相等(对应线段也可能在一条直线上)
课堂小结
P30:习题5.4:第1、2题.
布置作业
人教版 七年级数学下册
第5章 相交线与平行线
5.4 平移
第1课时 平移及其性质
学习目标
1. 通过具体实例认识平移.
2. 探索平移的基本性质.
3. 认识并欣赏平移在自然界和现实生活中的应用.
移动方向怎么样?
引入新课
移动方向怎么样?
把一个图形整体沿某一直线方向移动,会得到一个新图形,新图形与原图形的形状和大小完全相同,而这种图形的移动,叫做平移.
A
B
C
一、平移的定义
新知讲解
判断此图是平移吗?
不是
因为图形整体沿某一直线方向移动
易错辨析
图形的平移一定是水平或竖直的吗?
图形的平移不一定是水平的,也不一定是竖直的.
如:左图鸟的飞行也是平移
图形平移的路径是直线即可
易错辨析
问题:我们先观看以下几种生活现象,再想一想平移是由什么决定的?
新知探究
图形的平移由移动的方向和距离决定.
归纳总结
可以把一张半透明的纸盖在图上,先描出第一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个……(如图)
如何在一张纸上画出一排形状和大小如下图的雪人?
新知探究
问:雪人的形状、大小、位置在运动前后是否发生了变化?
答:雪人的形状不变,大小不变,位置改变.
平移不改变图形的形状、大小
平移改变图形的位置
简述为:“一变两不变”
二、平移的基本性质1
新知归纳
1. 下图中的变换属于平移的有哪些?
F
A
B
D
E
C
旋转
轴对称
针对训练
√
2. 下面 2,3,4,5 幅图中哪幅图是由1平移得到的?
1
2
3
4
5
(1)
(2)
2
3
4
5
1
√
√
C
4. 平移改变的是图形的( )
A. 位置 B. 大小
C. 形状 D. 位置、形状和大小
A
区分平移、旋转和轴对称.
易错辨析
甲
乙
雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是怎样运动的?它运动到了什么位置?帽顶B呢?
A运动到A′ ,B运动到B′.
新知探究
甲
乙
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点就是对应点.
可以发现:AA′∥BB′∥CC′并且AA′=BB′=CC′
再作出连接其他对应点的线段,仍有前面的关系吗?
有
B
A
C
A′
B′
C′
连接几组对应点(如:A与A′ ,B与B′ ,C与C′ )观察得到的线段,它们的位置、长短有什么关系?
D
D′
注意:平行线段是指线段所在的直线平行
动动手:用三角板、直尺画平行线.
P
Q
D
E
F
A
B
C
观察:线段AB与DE的位置关系与数量关系.
直尺PQ是倾斜放置,用三角板能否画 出平行线?
AB//DE
AB=DE
注意:在平移过程中,对应线段也可能在一条直线上(如:BC与EF)
经过平移,对应点所连的线段平行且相等
图形中的每一个点都移动了相同的距离
三、平移的基本性质2
新知归纳
1. 在图形平移中,下面说法错误的是( )
A. 图形上任意点移动的方向相同
B. 图形上任意点移动的距离相等
C. 图形上任意两点的连线的长度改变
D. 图形在平移前后形状和大小不发生改变
C
当堂巩固
2. 如图,△ABC平移到△DEF的位置,请回答下列问题.
解:对应点:
点A和___点、点B和__点、点C和__点;
经过平移后,有哪些线段是相等的?
D
E
F
线段AB和____、线段BC和____、线段AC和_____;
DE
EF
DF
1.(4分)(2020 上海6/25)如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
【解答】解:如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
∵四边形ABEF向右平移可以与四边形EFDC重合,
∴平行四边形ABCD是平移重合图形,
故选:A.
感受中考
【解答】解:∵△ABC沿BC边向右平移2个单位,得到△DEF,
∴AD=CF=2,AC=DF,
∵△ABC的周长为8,
∴AB+BC+AC=8,
∴AB+BC+DF=8,
∴四边形ABFD的周长= AB+BC+CF +DF+AD= AB+BC+ DF+AD+CF=8+2+2=12.
故答案为12.
2.(2分)(2020 青海4/28)如图,将周长为8的△ABC沿BC边向右平移2个单位,得到△DEF,则四边形ABFD的周长为 .
感受中考
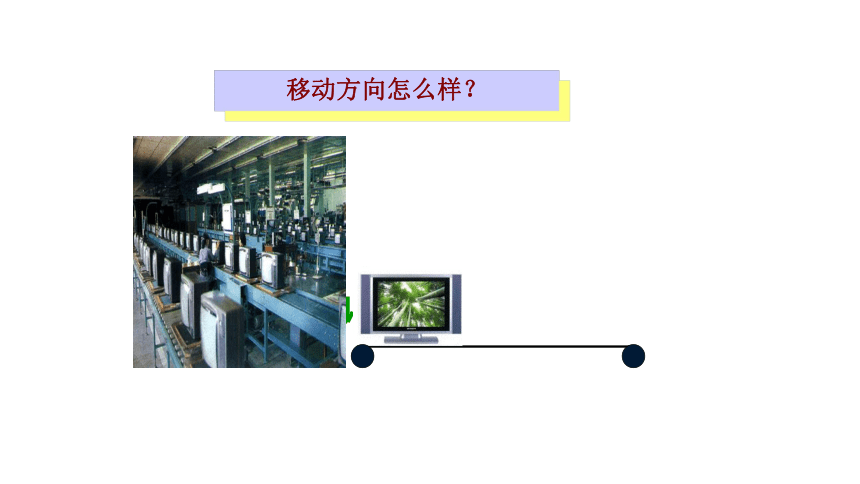
平移在自然界和现实生活中的应用
工厂里的传输带,电梯等
1. 平移的定义
把一个图形整体沿某一直线方向移动,会得到一个新图形,新图形与原图形的形状和大小完全相同,而这种图形的移动,叫做平移.
2. 平移的基本性质
(1)平移不改变图形的形状、大小,改变图形位置
(2)对应点所连线段平行且相等(对应线段也可能在一条直线上)
课堂小结
P30:习题5.4:第1、2题.
布置作业
