26.2 实际问题与反比例函数(第1课时) 课件(共46张PPT)
文档属性
| 名称 | 26.2 实际问题与反比例函数(第1课时) 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 976.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-10 17:35:47 | ||
图片预览











文档简介
(共46张PPT)
人教版 九年级数学下册
第26章 反比例函数
26.2 实际问题与反比例函数
第1课时 实际问题中的反比例函数
学习目标
1. 能够通过分析实际问题中变量之间的关系,建立反比例函数模型解决问题,进一步提高运用函数的图象、性质的综合能力.
2. 能够根据实际问题确定自变量的取值范围.
回顾一次函数和二次函数的学习过程,在学习了反比例函数的定义和性质后,接下来应该研究什么?如何研究?
前面我们结合实际问题讨论了反比例函数,看到了反比例函数在分析和解决实际问题的作用. 下面我们进一步探讨如何利用反比例函数解决实际问题.
复习回顾
例1:市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
(1)储存室的底面积 S(单位:m2)与其深度 d
(单位:m)有怎样的函数关系?
(2)公司决定把储存室的底面积 S 定为 500 m2,
施工队施工时应该向地下掘进多深?
(3)当施工队按(2)中的计划掘进到地下 15 m 时,公司临时改变计划,把储存室的深度改为 15 m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)?
典例分析
一、用反比例函数解决面积、体积、容积类问题
小组讨论:
1. 圆柱体的体积公式是什么?
2. 第(2)问和第(3)问与过去所学的解分式方程和求代数式的值的问题有何联系?
合作探究
(1)储存室的底面积 S(单位:m2)与其深度 d(单位:m)有怎样的函数关系?
解:(1)根据圆柱的体积公式,得 Sd =104,
变形得
即储存室的底面积 S 是其深度 d 的反比例函数.
(2)公司决定把储存室的底面积 S 定为 500 m2,施工队施工时应该向地下掘进多深?
解得 d = 20(m).
解:把 S = 500 代入
得
如果把储存室的底面积定为 500 m2,施工时应向地下掘进 20 m 深.
(3)当施工队按(2)中的计划掘进到地下 15 m时,公司临时改变计划,把储存室的深度改为 15 m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)?
解得 S≈666.67(m2).
当储存室的深度为 15 m 时,底面积约为 666.67 m2.
解:把 d =15 代入 ,
得 .
反思小结:第(1) 问首先要弄清此题中各数量间的关系,容积为104,底面积是S,深度为d,满足基本公式:圆柱的体积=底面积×高,由题意知S是函数,d是自变量,改写后所得的函数关系式是反比例函数的形式. 第(2)问实际上是已知函数S的值,求自变量d的取值,第(3)问则是与第(2)问相反.
我们学习过反比例函数,例如,当矩形面积一定时,长a是宽b的反比例函数,其函数关系式可以写为 (S为常数, S ≠0).
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.
实例: ;函数关系式: .
解:本题通过范例,再联系日常生活、生产或学习当中可以举出许许多多与反比例函数有关的例子来,例如:实例,三角形的面积S一定时,三角形底边长y是高x的反比例函数,其函数关系式可以写为 (S为常数,S ≠0).
针对训练
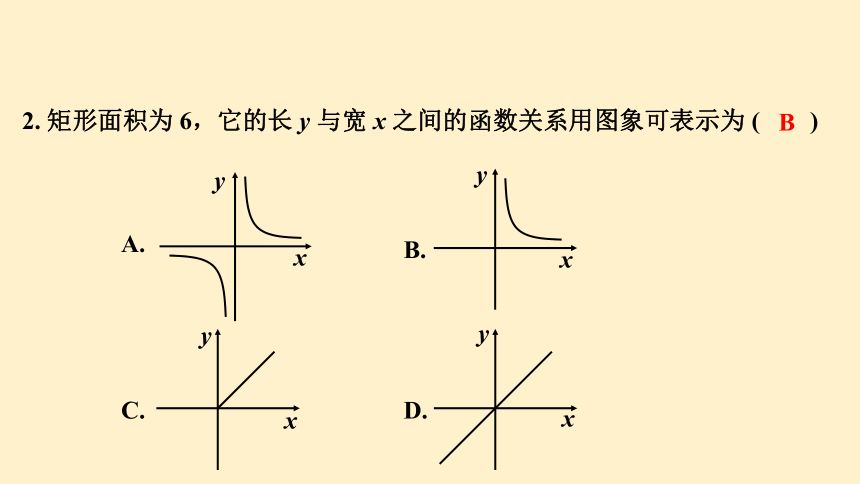
2. 矩形面积为 6,它的长 y 与宽 x 之间的函数关系用图象可表示为 ( )
B
A.
B.
C.
D.
x
y
x
y
x
y
x
y
3. 如图,某玻璃器皿制造公司要制造一种容积为1升 (1升=1立方分米)的圆锥形漏斗.
(1) 漏斗口的面积 S (单位:dm2)与漏斗的深 d (单位: dm) 有怎样的函数关系
d
解:
(3) 如果漏斗口的面积为 60 cm2,则漏斗的深为多少
解:60 cm2 = 0.6 dm2,把 S =0.6 代入解析式,
得 d =5.
所以漏斗的深为 5 dm.
(2) 如果漏斗的深为1 dm,那么漏斗口的面积为多少 dm2?
解:把 d =1 代入解析式,得 S =3.所以漏斗口的面积为 3 dm2.
d
例2:码头工人每天往一艘轮船上装载30 吨货物,装载完毕恰好用了 8 天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度 v(单位:吨/天)与卸货天数 t 之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过 5 天卸载完毕,那么平均每天至少要卸载多少吨?
典例分析
二、用反比例函数解决工程问题
小组讨论:题目中蕴含的等量关系是什么?我们知道“至少”对应于不等号“≥”,那么需要用不等式来解决第(2)问吗?说说看.
分析:根据装货速度×装货时间=货物的总量,可以求出轮船装载货物的总量;再根据卸货速度=货物的总量÷卸货时间,得到v与t的函数式.
合作探究
解:(1)设轮船上的货物有k吨,由已知条件得 k=30×8=240(吨),
例2:码头工人每天往一艘轮船上装载30 吨货物,装载完毕恰好用了 8 天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度 v(单位:吨/天)与卸货天数 t 之间有怎样的函数关系?
所以 v 关于 t 的函数解析式为 .
(2)由于遇到紧急情况,要求船上的货物不超过 5 天卸载完毕,那么平均每天至少要卸载多少吨?
解法一:把 t=5 代入 ,得
从结果可以看出,如果全部货物恰好用5天卸载完,那么平均每天卸载48吨. 对于函数 来说,当t>0时,t越小,v越大. 所以若货物不超过5天卸载完,则平均每天至少要卸载48吨.
解法二:由题意知 t≤5 ,
由 ,得 .
∵t≤5,
∴ ≤5.
又v>0,
∴240≤5v.
∴v≥48(吨).
(2)由于遇到紧急情况,要求船上的货物不超过 5 天卸载完毕,那么平均每天至少要卸载多少吨?
反思小结:此题类似应用题中的“工程问题”,关系式为工作总量=工作速度×工作时间,由于题目中货物总量是不变的,两个变量分别是速度v和时间t,因此具有反比关系.第(2)问涉及了反比例函数的增减性,即当自变量t取最大值时,函数值v取最小值是多少.
在解决反比例函数相关的实际问题中,若题目要求“至多”、“至少”,可以利用反比例函数的增减性来解答 .
1. 完成某项任务可获得500元报酬,考虑由x人完成这项任务,试写出人均报酬y(元)与人数x(人)之间的函数关系式 .
2. 学校锅炉旁建有一个储煤库,开学时购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完. 若每天的耗煤量为x吨,那么这批煤能维持y 天.
(1)则y与x之间有怎样的函数关系?
(2)画函数图象
(3)若每天节约0.1吨,则这批煤能维持多少天?
针对训练
解:(1)煤的总量为:0.6×150=90吨,
∵x y=90,∴y= .
(2)函数的图象为右图:
(3)∵每天节约0.1吨煤,
∴每天的用煤量为0.6-0.1=0.5吨,
∴y= = =180天,
∴这批煤能维持180天.
3. 某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把 1200 立方米的生活垃圾运走.
(1) 假如每天能运 x 立方米,所需时间为 y 天,写出 y与 x 之间的函数关系式;
解:
(2) 若每辆拖拉机一天能运 12 立方米,则 5 辆这样的拖拉机要用多少天才能运完?
解:x =12×5=60,代入函数解析式得
答:若每辆拖拉机一天能运 12 立方米,则 5 辆这样的拖拉机要用 20 天才能运完.
(3) 在 (2) 的情况下,运了 8 天后,剩下的任务要在不超过 6 天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
解:运了8天后剩余的垃圾有
1200-8×60=720 (立方米),
剩下的任务要在不超过6天的时间完成,则每天
至少运 720÷6=120 (立方米),
所以需要的拖拉机数量是:120÷12=10 (辆),
即至少需要增加拖拉机10-5=5 (辆).
面积一定时,矩形的长与宽成反比;面积一定时,三角形的一边长与这边的高成反比;体积一定时,柱体的底面积与高成反比等.建立反比例函数模型解决实际问题时,要注意自变量的取值范围.
归纳
1. 面积为 2 的直角三角形一直角边长为x,另一直角边长为 y,则 y 与 x 的变化规律用图象可大致表示为 ( )
A.
x
y
1
O
2
x
y
4
O
4
B.
x
y
1
O
4
C.
x
y
1
O
4
1
4
D.
C
随堂练习
2.一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480
C.v= D.v=
A
3.A、B两城市相距720千米,一列火车从A城去B城.
(1)火车的速度v(千米/时)和行驶的时间t(时)之间的函数关系是______.
(2)若到达目的地后,按原路匀速返回,并要求在3小时内回到A城,则返回的速度不能低于____________.
240千米/时
4. 体积为 20 cm3 的滴胶做成圆柱体模型,圆柱的高度 y (单位:cm) 与底面积S (单位:cm2)的函数关系为 ,若要使做出来的圆柱体粗 1 cm2,则圆柱的高度是 cm.
20
5. A、B两城市相距720千米,一列火车从A城去B城.
(1) 火车的速度 v (千米/时) 和行驶的时间 t (时) 之间的函数关系是________.
(2) 若到达目的地后,按原路匀速返回,并要求在 3 小时内回到 A 城,则返回的速度不能低于____________.
240千米/时
6. 在□ABCD中,AB=4cm,BC=1cm,E是CD边上一动点,AE、BC的延长线交于点F,设DE=x(cm),BF=y(cm).则y与x之间的函数关系式为____________,并写出自变量x的取值范围为____________.
7. 设△ABC中BC边的长为x(cm),BC上的高AD为y(cm).已知y关于x的函数图象过点(3,4).
(1)求y关于x的函数解析式和△ ABC 的面积.
(2)画出函数的图象,并利用图象,求当2<x<8时y的取值范围.
解:(1)由题意,S△ABC= xy,把点(3,4)代入,得
S △ABC= xy= ×3×4=6,
∴y关于x的函数解析式是y= ,△ABC的面积是6厘米2;
(2)如图所示:当x=2时,y=6;
当x=8时,y=1.5,
由函数y= 图象的性质得,
在第一象限y随x的增大而减小,
∴当2<x<8时,y的取值范围是1.5<y<6.
1.某项工程需要沙石料2×106立方米,阳光公司承担了该工程运送沙石料的任务.
(1)在这项任务中平均每天的工作量v(立方米/天)与完成任务所需要的时间t(天)之间具有怎样的函数关系写出这个函数关系式.
(2)阳光公司计划投入A型卡车200辆,每天一共可以运送沙石料2×104立方米,则完成全部运送任务需要多少天如果工作了25天后,由于工程进度的需要,公司准备再投入A型卡车120辆.在保持每辆车每天工作量不变的前提下,问:是否能提前28天完成任务?
能力提升
解:(1)成反比例函数关系v= ;
(2)把V=2×104代入函数式得:t=100天,
每辆车每天能运送石料100(立方米),
(2×106-2×104×25)÷[(200+120)×100]=46.875(天),
因为100-25-46.875=28.125>28,
所以能提前28天完成任务.
2. 某户现在有若干度电,现在知道:按每天用6度电计算,五个月(按15天计算) 刚好用完. 若每天的耗电量为 x 度,那么这些电能维持 y 天.
(1) 则 y 与 x 之间有怎样的函数关系?
解:电的总量为:6×15=90 (度),
根据题意有
(x>0).
(2) 画出函数的图象;
解:如右图所示.
30
90
1
x
y
O
3
(3) 若每天节约 1 度,则这些电能维持多少天?
解:∵ 每天节约 1 度电,
∴ 每天的用电量为 6-1=5 (度),
∴ 这些电能维持 18 天.
3. 王强家离工作单位的距离为3600 米,他每天骑自行车上班时的速度为 v 米/分,所需时间为 t 分钟.
(1) 速度 v 与时间 t 之间有怎样的函数关系?
解:
(2) 若王强到单位用 15 分钟,那么他骑车的平均速度是多少?
解:把 t =15代入函数的解析式,得:
答:他骑车的平均速度是 240 米/分.
(3) 如果王强骑车的速度最快为 300 米/分,那他至少需要几分钟到达单位
解:把 v =300 代入函数解析式得:
解得:t =12.
答:他至少需要 12 分钟到达单位.
4. 在某村河治理工程施工过程中,某工程队接受一项开挖水渠的工程,所需天数 y (天) 与每天完成的工程量 x (m/天) 的函数关系图象如图所示.
(1) 请根据题意,求 y 与 x 之间的函数表达式;
50
24
x(m/天)
y(天)
O
解:
(2) 若该工程队有 2 台挖掘机,每台挖掘机每天能够开挖水渠 15 m,问该工程队需用多少天才能完成此项任务?
解:由图象可知共需开挖水渠 24×50=1200 (m),
2 台挖掘机需要 1200÷(2×15)=40 (天).
(3) 如果为了防汛工作的紧急需要,必须在一个月内 (按 30 天计算)完成任务,那么每天至少要完成多少米?
解:1200÷30=40 (m),
故每天至少要完成40 m.
(12分)(2020 呼和浩特24/24)已知某厂以t小时/千克的速度匀速生产某种产品(生产条件要求0.1<t≤1),且每小时可获得利润 元.
(1)某人将每小时获得的利润设为y元,发现t=1时,y=180,所以得出结论:每小时获得的利润,最少是180元,他是依据什么得出该结论的,用你所学数学知识帮他进行分析说明;
(2)若以生产该产品2小时获得利润1800元的速度进行生产,则1天(按8小时计算)可生产该产品多少千克;
(3)要使生产680千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
感受中考
【解答】解:(1)他是依据一次函数和反比例函数的增减性质得出结论;
令 ,当t=1时,y=180,
∵当0.1<t≤1时, 随t的增大而减小, -3t也随t的增大而减小,
∴ 的值随t的增大而减小,
∴ 随t的增大而减小,
∴当t=1时,y取最小,
∴他的结论正确.
(2)由题意得: ,
整理得:-3t2-14t+5=0,
解得: , (舍),
即以 小时/千克的速度匀速生产产品,则1天(按8小时计算)可生产该
产品 千克.
∴1天(按8小时计算)可生产该产品24千克;
(3)生产680千克该产品获得的利润为: ,
整理得:y=40800(-3t2+t+5),
∴当 时,y最大,且最大值为207400元.
∴该厂应该选取 小时/千克的速度生产,此时最大利润为207400元.
反比例函数
实际问题中的
过程:
分析实际情境→建立函数模型→明确数学问题
注意:
实际问题中的两个变量往往都只能取非负值;
作实际问题中的函数图象时,横、纵坐标的单
位长度不一定相同.
实际问题
反比例函数
建立数学模型
运用数学知识解决
课堂小结
P16:习题26.2:第7题.
P17:习题26.2:第9题.
P22:复习题26:第11题.
布置作业
人教版 九年级数学下册
第26章 反比例函数
26.2 实际问题与反比例函数
第1课时 实际问题中的反比例函数
学习目标
1. 能够通过分析实际问题中变量之间的关系,建立反比例函数模型解决问题,进一步提高运用函数的图象、性质的综合能力.
2. 能够根据实际问题确定自变量的取值范围.
回顾一次函数和二次函数的学习过程,在学习了反比例函数的定义和性质后,接下来应该研究什么?如何研究?
前面我们结合实际问题讨论了反比例函数,看到了反比例函数在分析和解决实际问题的作用. 下面我们进一步探讨如何利用反比例函数解决实际问题.
复习回顾
例1:市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
(1)储存室的底面积 S(单位:m2)与其深度 d
(单位:m)有怎样的函数关系?
(2)公司决定把储存室的底面积 S 定为 500 m2,
施工队施工时应该向地下掘进多深?
(3)当施工队按(2)中的计划掘进到地下 15 m 时,公司临时改变计划,把储存室的深度改为 15 m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)?
典例分析
一、用反比例函数解决面积、体积、容积类问题
小组讨论:
1. 圆柱体的体积公式是什么?
2. 第(2)问和第(3)问与过去所学的解分式方程和求代数式的值的问题有何联系?
合作探究
(1)储存室的底面积 S(单位:m2)与其深度 d(单位:m)有怎样的函数关系?
解:(1)根据圆柱的体积公式,得 Sd =104,
变形得
即储存室的底面积 S 是其深度 d 的反比例函数.
(2)公司决定把储存室的底面积 S 定为 500 m2,施工队施工时应该向地下掘进多深?
解得 d = 20(m).
解:把 S = 500 代入
得
如果把储存室的底面积定为 500 m2,施工时应向地下掘进 20 m 深.
(3)当施工队按(2)中的计划掘进到地下 15 m时,公司临时改变计划,把储存室的深度改为 15 m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)?
解得 S≈666.67(m2).
当储存室的深度为 15 m 时,底面积约为 666.67 m2.
解:把 d =15 代入 ,
得 .
反思小结:第(1) 问首先要弄清此题中各数量间的关系,容积为104,底面积是S,深度为d,满足基本公式:圆柱的体积=底面积×高,由题意知S是函数,d是自变量,改写后所得的函数关系式是反比例函数的形式. 第(2)问实际上是已知函数S的值,求自变量d的取值,第(3)问则是与第(2)问相反.
我们学习过反比例函数,例如,当矩形面积一定时,长a是宽b的反比例函数,其函数关系式可以写为 (S为常数, S ≠0).
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.
实例: ;函数关系式: .
解:本题通过范例,再联系日常生活、生产或学习当中可以举出许许多多与反比例函数有关的例子来,例如:实例,三角形的面积S一定时,三角形底边长y是高x的反比例函数,其函数关系式可以写为 (S为常数,S ≠0).
针对训练
2. 矩形面积为 6,它的长 y 与宽 x 之间的函数关系用图象可表示为 ( )
B
A.
B.
C.
D.
x
y
x
y
x
y
x
y
3. 如图,某玻璃器皿制造公司要制造一种容积为1升 (1升=1立方分米)的圆锥形漏斗.
(1) 漏斗口的面积 S (单位:dm2)与漏斗的深 d (单位: dm) 有怎样的函数关系
d
解:
(3) 如果漏斗口的面积为 60 cm2,则漏斗的深为多少
解:60 cm2 = 0.6 dm2,把 S =0.6 代入解析式,
得 d =5.
所以漏斗的深为 5 dm.
(2) 如果漏斗的深为1 dm,那么漏斗口的面积为多少 dm2?
解:把 d =1 代入解析式,得 S =3.所以漏斗口的面积为 3 dm2.
d
例2:码头工人每天往一艘轮船上装载30 吨货物,装载完毕恰好用了 8 天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度 v(单位:吨/天)与卸货天数 t 之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过 5 天卸载完毕,那么平均每天至少要卸载多少吨?
典例分析
二、用反比例函数解决工程问题
小组讨论:题目中蕴含的等量关系是什么?我们知道“至少”对应于不等号“≥”,那么需要用不等式来解决第(2)问吗?说说看.
分析:根据装货速度×装货时间=货物的总量,可以求出轮船装载货物的总量;再根据卸货速度=货物的总量÷卸货时间,得到v与t的函数式.
合作探究
解:(1)设轮船上的货物有k吨,由已知条件得 k=30×8=240(吨),
例2:码头工人每天往一艘轮船上装载30 吨货物,装载完毕恰好用了 8 天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度 v(单位:吨/天)与卸货天数 t 之间有怎样的函数关系?
所以 v 关于 t 的函数解析式为 .
(2)由于遇到紧急情况,要求船上的货物不超过 5 天卸载完毕,那么平均每天至少要卸载多少吨?
解法一:把 t=5 代入 ,得
从结果可以看出,如果全部货物恰好用5天卸载完,那么平均每天卸载48吨. 对于函数 来说,当t>0时,t越小,v越大. 所以若货物不超过5天卸载完,则平均每天至少要卸载48吨.
解法二:由题意知 t≤5 ,
由 ,得 .
∵t≤5,
∴ ≤5.
又v>0,
∴240≤5v.
∴v≥48(吨).
(2)由于遇到紧急情况,要求船上的货物不超过 5 天卸载完毕,那么平均每天至少要卸载多少吨?
反思小结:此题类似应用题中的“工程问题”,关系式为工作总量=工作速度×工作时间,由于题目中货物总量是不变的,两个变量分别是速度v和时间t,因此具有反比关系.第(2)问涉及了反比例函数的增减性,即当自变量t取最大值时,函数值v取最小值是多少.
在解决反比例函数相关的实际问题中,若题目要求“至多”、“至少”,可以利用反比例函数的增减性来解答 .
1. 完成某项任务可获得500元报酬,考虑由x人完成这项任务,试写出人均报酬y(元)与人数x(人)之间的函数关系式 .
2. 学校锅炉旁建有一个储煤库,开学时购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完. 若每天的耗煤量为x吨,那么这批煤能维持y 天.
(1)则y与x之间有怎样的函数关系?
(2)画函数图象
(3)若每天节约0.1吨,则这批煤能维持多少天?
针对训练
解:(1)煤的总量为:0.6×150=90吨,
∵x y=90,∴y= .
(2)函数的图象为右图:
(3)∵每天节约0.1吨煤,
∴每天的用煤量为0.6-0.1=0.5吨,
∴y= = =180天,
∴这批煤能维持180天.
3. 某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把 1200 立方米的生活垃圾运走.
(1) 假如每天能运 x 立方米,所需时间为 y 天,写出 y与 x 之间的函数关系式;
解:
(2) 若每辆拖拉机一天能运 12 立方米,则 5 辆这样的拖拉机要用多少天才能运完?
解:x =12×5=60,代入函数解析式得
答:若每辆拖拉机一天能运 12 立方米,则 5 辆这样的拖拉机要用 20 天才能运完.
(3) 在 (2) 的情况下,运了 8 天后,剩下的任务要在不超过 6 天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
解:运了8天后剩余的垃圾有
1200-8×60=720 (立方米),
剩下的任务要在不超过6天的时间完成,则每天
至少运 720÷6=120 (立方米),
所以需要的拖拉机数量是:120÷12=10 (辆),
即至少需要增加拖拉机10-5=5 (辆).
面积一定时,矩形的长与宽成反比;面积一定时,三角形的一边长与这边的高成反比;体积一定时,柱体的底面积与高成反比等.建立反比例函数模型解决实际问题时,要注意自变量的取值范围.
归纳
1. 面积为 2 的直角三角形一直角边长为x,另一直角边长为 y,则 y 与 x 的变化规律用图象可大致表示为 ( )
A.
x
y
1
O
2
x
y
4
O
4
B.
x
y
1
O
4
C.
x
y
1
O
4
1
4
D.
C
随堂练习
2.一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480
C.v= D.v=
A
3.A、B两城市相距720千米,一列火车从A城去B城.
(1)火车的速度v(千米/时)和行驶的时间t(时)之间的函数关系是______.
(2)若到达目的地后,按原路匀速返回,并要求在3小时内回到A城,则返回的速度不能低于____________.
240千米/时
4. 体积为 20 cm3 的滴胶做成圆柱体模型,圆柱的高度 y (单位:cm) 与底面积S (单位:cm2)的函数关系为 ,若要使做出来的圆柱体粗 1 cm2,则圆柱的高度是 cm.
20
5. A、B两城市相距720千米,一列火车从A城去B城.
(1) 火车的速度 v (千米/时) 和行驶的时间 t (时) 之间的函数关系是________.
(2) 若到达目的地后,按原路匀速返回,并要求在 3 小时内回到 A 城,则返回的速度不能低于____________.
240千米/时
6. 在□ABCD中,AB=4cm,BC=1cm,E是CD边上一动点,AE、BC的延长线交于点F,设DE=x(cm),BF=y(cm).则y与x之间的函数关系式为____________,并写出自变量x的取值范围为____________.
7. 设△ABC中BC边的长为x(cm),BC上的高AD为y(cm).已知y关于x的函数图象过点(3,4).
(1)求y关于x的函数解析式和△ ABC 的面积.
(2)画出函数的图象,并利用图象,求当2<x<8时y的取值范围.
解:(1)由题意,S△ABC= xy,把点(3,4)代入,得
S △ABC= xy= ×3×4=6,
∴y关于x的函数解析式是y= ,△ABC的面积是6厘米2;
(2)如图所示:当x=2时,y=6;
当x=8时,y=1.5,
由函数y= 图象的性质得,
在第一象限y随x的增大而减小,
∴当2<x<8时,y的取值范围是1.5<y<6.
1.某项工程需要沙石料2×106立方米,阳光公司承担了该工程运送沙石料的任务.
(1)在这项任务中平均每天的工作量v(立方米/天)与完成任务所需要的时间t(天)之间具有怎样的函数关系写出这个函数关系式.
(2)阳光公司计划投入A型卡车200辆,每天一共可以运送沙石料2×104立方米,则完成全部运送任务需要多少天如果工作了25天后,由于工程进度的需要,公司准备再投入A型卡车120辆.在保持每辆车每天工作量不变的前提下,问:是否能提前28天完成任务?
能力提升
解:(1)成反比例函数关系v= ;
(2)把V=2×104代入函数式得:t=100天,
每辆车每天能运送石料100(立方米),
(2×106-2×104×25)÷[(200+120)×100]=46.875(天),
因为100-25-46.875=28.125>28,
所以能提前28天完成任务.
2. 某户现在有若干度电,现在知道:按每天用6度电计算,五个月(按15天计算) 刚好用完. 若每天的耗电量为 x 度,那么这些电能维持 y 天.
(1) 则 y 与 x 之间有怎样的函数关系?
解:电的总量为:6×15=90 (度),
根据题意有
(x>0).
(2) 画出函数的图象;
解:如右图所示.
30
90
1
x
y
O
3
(3) 若每天节约 1 度,则这些电能维持多少天?
解:∵ 每天节约 1 度电,
∴ 每天的用电量为 6-1=5 (度),
∴ 这些电能维持 18 天.
3. 王强家离工作单位的距离为3600 米,他每天骑自行车上班时的速度为 v 米/分,所需时间为 t 分钟.
(1) 速度 v 与时间 t 之间有怎样的函数关系?
解:
(2) 若王强到单位用 15 分钟,那么他骑车的平均速度是多少?
解:把 t =15代入函数的解析式,得:
答:他骑车的平均速度是 240 米/分.
(3) 如果王强骑车的速度最快为 300 米/分,那他至少需要几分钟到达单位
解:把 v =300 代入函数解析式得:
解得:t =12.
答:他至少需要 12 分钟到达单位.
4. 在某村河治理工程施工过程中,某工程队接受一项开挖水渠的工程,所需天数 y (天) 与每天完成的工程量 x (m/天) 的函数关系图象如图所示.
(1) 请根据题意,求 y 与 x 之间的函数表达式;
50
24
x(m/天)
y(天)
O
解:
(2) 若该工程队有 2 台挖掘机,每台挖掘机每天能够开挖水渠 15 m,问该工程队需用多少天才能完成此项任务?
解:由图象可知共需开挖水渠 24×50=1200 (m),
2 台挖掘机需要 1200÷(2×15)=40 (天).
(3) 如果为了防汛工作的紧急需要,必须在一个月内 (按 30 天计算)完成任务,那么每天至少要完成多少米?
解:1200÷30=40 (m),
故每天至少要完成40 m.
(12分)(2020 呼和浩特24/24)已知某厂以t小时/千克的速度匀速生产某种产品(生产条件要求0.1<t≤1),且每小时可获得利润 元.
(1)某人将每小时获得的利润设为y元,发现t=1时,y=180,所以得出结论:每小时获得的利润,最少是180元,他是依据什么得出该结论的,用你所学数学知识帮他进行分析说明;
(2)若以生产该产品2小时获得利润1800元的速度进行生产,则1天(按8小时计算)可生产该产品多少千克;
(3)要使生产680千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
感受中考
【解答】解:(1)他是依据一次函数和反比例函数的增减性质得出结论;
令 ,当t=1时,y=180,
∵当0.1<t≤1时, 随t的增大而减小, -3t也随t的增大而减小,
∴ 的值随t的增大而减小,
∴ 随t的增大而减小,
∴当t=1时,y取最小,
∴他的结论正确.
(2)由题意得: ,
整理得:-3t2-14t+5=0,
解得: , (舍),
即以 小时/千克的速度匀速生产产品,则1天(按8小时计算)可生产该
产品 千克.
∴1天(按8小时计算)可生产该产品24千克;
(3)生产680千克该产品获得的利润为: ,
整理得:y=40800(-3t2+t+5),
∴当 时,y最大,且最大值为207400元.
∴该厂应该选取 小时/千克的速度生产,此时最大利润为207400元.
反比例函数
实际问题中的
过程:
分析实际情境→建立函数模型→明确数学问题
注意:
实际问题中的两个变量往往都只能取非负值;
作实际问题中的函数图象时,横、纵坐标的单
位长度不一定相同.
实际问题
反比例函数
建立数学模型
运用数学知识解决
课堂小结
P16:习题26.2:第7题.
P17:习题26.2:第9题.
P22:复习题26:第11题.
布置作业
